基于孤立森林方法的催化裂化装置排污数据异常识别
陈 冲,何 为,2,钟田福,王 晶
(1.中国石油大学(北京) 信息科学与工程学院,北京 102249;2.中国石油集团安全环保技术研究院有限公司 HSE 检测中心,北京102206)
引 言
催化裂化装置产生的废气是空气环境的潜在威胁之一。90万吨/年催化裂化装置烟气排放经过烟气轮机做功后进入余热锅炉,正常情况下SO2排放浓度为800~2 000 mg/m3,NOx的排放浓度为140~300 mg/m3,均超过我国于2015年实施的GB31570—2015《石油炼制工业污染物排放标准》中规定的50 mg/m3与100 mg/m3的排放标准。基于历史数据(生产数据、监测数据等)构建催化裂化装置的预测模型,根据不同工况预测烟气排放是控制催化裂化装置烟气排放的有效方法之一。目前,我国已初步形成了环保信息网络,环境监测数据由生产企业上报,地方环保部门收集、上报并存储到环境保护监测数据库中。然而,在数据采集、存储设备本身以及采集人员、采集过程等各个环节中,都不可避免地引入异常数据。异常数据的引入可能引起数据的伪相关(spurious correlation)等问题,从而影响数据的可用性。因此,为了保证数据分析与处理结果的准确性,在使用数据之前,有必要对数据进行异常识别。
异常数据可由噪声、系统自身、客观因素以及复杂环境等原因造成,导致个别数据与整体数据规律不一致,大多数研究者认同来自Hawkins[1]的定义:“异常值是指样本中的个别值,其数值明显偏离它(或它们)所属样本的其余观测值”。无监督异常检测方法简单、高效,已经被广泛应用于异常检测中。Yamanishi等人[2]使用高斯混合模型拟合实际数据,并根据模型筛选异常数据。基于聚类的异常数据检测方法主要有CBLOF(Cluster-Based Local Outlier Factor)[3]、LDCOF(Local Density Cluster-Based Outlier Factor)[4]、CMGOS(Clustering-based Multivariate Gaussian Outlier Score)[5]等[6]。刘旋等[7]提出了一种基于逆K最近邻的密度峰值异常检测方法(Rknn-DP),在多种数据集下与ABOD(Angle-Based Outlier Detection)[8]、CBLOF、LSCP(Locally Selective Combination in Parallel outlier ensembles)[9]、HBOS(Histogram-based Outlier Score)[10]及孤立森林算法(iForest,Isolation Forest)[11]进行了实验对比,证明了Rknn-DP算法的有效性。基于距离的方法主要原理是根据数据样本与其余样本点之间的距离是否超过阈值来检测异常样本[12]。Breunig等[13]阐述了局部异常数据的定义,提出了局部异常因子算法LOF(Local Outlier Factor),基于可达距离、可达密度定义局部离群因子,衡量样本的异常程度,从而实现异常值检测。Du等[14]提出了利用统计参数进行局部异常检测的方法,结合聚类与密度方法实现了大数据的异常值检测。与以上几种基于密度与距离的算法不同,Liu等[11]提出孤立森林算法,通过借鉴随机森林的集成学习提高算法的鲁棒性,并采用树型结构减小了计算量,且能保证较高的准确度。Yu等[15]结合LOF的优点对孤立森林算法进行了改进,先利用LOF算法对原始数据进行异常检测,再利用孤立森林算法对检测结果进行筛选,从而提高检测结果的稳定性和精确度,但是也增加了算法的计算消耗。Liu等[16]基于分裂选择标准(SC,Split-selection Criterion)对孤立森林算法进行改进,提出SCiForest(Split-selection Criterion iForest)检测聚类异常。Ding等[17]提出了iForestASD算法,该算法通过滑窗对实时数据分割检测,有效地解决了流动数据的异常检测问题。Aryal等[18]针对孤立森林无法有效检测局部异常数据的问题,提出了一种基于相对质量改进的孤立森林算法。该算法利用相对质量代替距离点计算,更加有效地体现了数据与邻近数据的分布规律,解决了局部异常数据在异常数据检测中出现的遮掩问题。Bandaragoda等[19]提出了一种基于距离的改进方法——使用K近邻的孤立方法(iNNE,isolation using Nearest Neighbour Ensemble),其运行速度明显快于现有的最近邻方法,并且解决了孤立森林算法局部异常检测、缺少属性数据的异常检测以及正常实例包围的异常检测情况。
本文以中国石油某炼化企业350万吨/年重油催化裂化装置为研究对象,基于孤立森林算法对该催化裂化装置所排放烟气中氮氧化物的监测数据开展数据异常识别研究。从算法的分支步骤与局部度量方面,改进孤立森林算法,提高算法性能。在多个标准数据集上与多个异常识别算法进行对比,验证算法的优越性。
1 异常数据识别方法
1.1 孤立森林算法
孤立森林算法的主要思想是对数据集进行随机切割,并通过集成学习的方式收敛数据切割的过程[11]。图1为一个数据集被随机切割的过程示例。其中,正常点xi需经过多次切割才能被识别出来,而异常点xo则很容易被切割出来,切割次数等于孤立树的深度,孤立森林根据数据点与根节点的深度来诊断数据的异常程度。
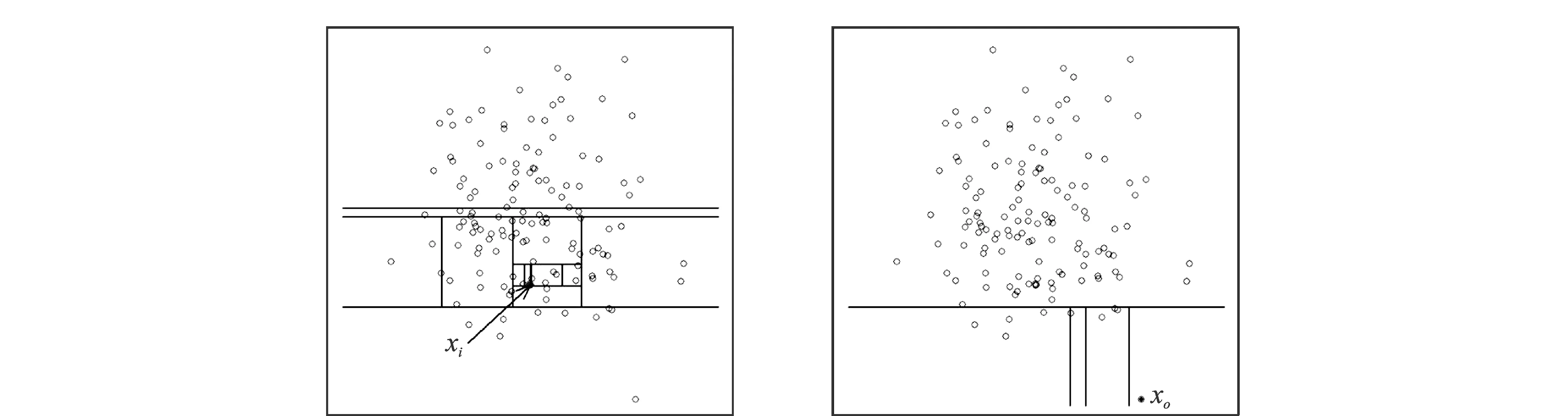
图1 正常值与异常值的分割过程Fig.1 Segmentation process of normal and abnormal observations
孤立森林算法过程主要包括两个部分。首先,利用原始数据随机采样生成t个孤立树,组成孤立森林模型;其次,数据样本遍历孤立树计算出异常分值。孤立树的构建步骤:
步骤1:从原始数据集中随机挑选T个数据点作为采样数据集;
步骤2:在采样数据集中随机选取维度,随机取值获得分割点p对样本集切割,切割后的数据分别放在左右叶子节点(在该维度中小于p的样本放在左叶子节点,大于等于p的样本放在右叶子节点);
步骤3:递归进行步骤2,切割数据集,直到满足停止条件(即样本数据集不可再分或孤立树的高度到达上限)。
建立t个孤立树之后(即生成了孤立森林模型),使未知数据点x遍历所有孤立树后记录x在每棵孤立树的层数h(x),计算x的平均深度。对平均深度进行归一化得到数据点x的异常分值。为了保证异常分值能够准确表示数据的异常程度,采用
(1)
进行计算。其中,E[·]为数据的期望;c(φ)起归一化作用,是由φ个点组成的二叉树的平均高度,即
(2)
式中:H(φ)=ln(φ)+ξ,ξ为欧拉常数。
由式(1)可以看出,S(x)越接近1表示样本x每次分割都被快速分割出来,是异常数据的可能性大;越接近0表示样本x远离根节点,是正常点的可能性大;当所有样本的S(x)都接近于0.5时,表明数据集中没有明显的异常数据。
1.2 分裂准则
分裂准则是在树节点分裂过程中所依据的标准,以选择最优的分裂属性与分裂点,是决策树算法中的核心问题之一,前期已有许多学者对此进行了研究[20-22]。在树节点分裂过程中,为了考虑数据的多个属性,优化模型性能,引入非轴平行于原始属性的随机超平面;同时,在随机超平面的选取过程中加入Sdgain检验指标,作为数据超平面的选择标准,以生成最佳超平面。由于树模型是一种集成学习模型,因此,单个超平面的效果对整体效果影响有限,所得到的模型作为一个整体仍然有效。在构造孤立树的每个节点时,随机生成τ个超平面,选择其中Sdgain最大的超平面作为最优超平面。超平面f(对应分割点p)的计算公式为
(3)
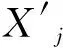
(4)
其中,YL∪YR=Y,Y为采样数据集X′在超平面f上的映射;avg(·)为计算平均值。在式(4)中,使用σ(Y)对计算值进行归一化。结合式(3)、式(4),寻找能够使Sdgain最大的p值生成最佳超平面。
1.3 相对质量
虽然孤立森林算法在许多实验中被证明是有效的,但是其无法有效识别局部异常数据。这是由于孤立森林算法的异常分数根据路径长度进行全局度量,导致无法考虑样本数据点与其邻近数据点之间的相对孤立关系。因此,Aryal等人[18]提出了一种简单但有效的方法——相对质量(Relative Mass),考虑样本数据点与邻近数据分布情况,以克服孤立森林在局部异常值检测方面的不足。相对质量是一种基于数据质量的局部度量方式。考虑一个数据集中的两个区域,其中一个区域是另一个区域的子集,数据的相对质量是覆盖该数据的两个区域中的数据质量的比例。在树模型结构中,数据的相对质量根据样本数据从根节点到叶节点中的质量比计算。
在孤立森林中,关注样本点x和它的局部邻域的相对质量用
(5)
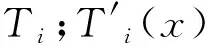
异常分数则由t个孤立树异常分数取均值得到,即
(6)
计算出每个节点的异常分数之后,根据异常分数的大小对各个节点进行排序,节点异常分数越大异常节点的概率越大。
1.4 改进的孤立森林算法实现过程
针对孤立森林算法在考虑数据整体属性以及局部异常检测中的局限,引入分裂准则与相对质量改进孤立森林算法,在提高模型(局部异常数据识别)精确度的同时减小计算消耗。在建立树模型时考虑数据的多维属性引入随机超平面,利用Sdgain筛选超平面,从而提高树模型的质量;利用相对质量改进异常分数的计算,解决将每个待测样本遍历所有孤立树的问题,避免内存浪费、减小模型时间复杂度。具体步骤如图2所示。
输入D——数据集;n——子采样大小;t——生成孤立树的数量。
步骤1:设置孤立树的最大高度,初始化孤立森林。
步骤2:构建孤立树。
步骤2.1:输入D′——构建孤立树的子数据集;q——生成超平面的属性数量;τ——随机生成的超平面数量;
步骤2.2:初始化生成孤立树算法参数;
步骤2.3:在τ个使用q个属性值生成的随机超平面中,筛选最大Sdgain所对应的最佳超平面f;
步骤2.4:将数据映射到最佳超平面f上,根据映射值将其分类;
步骤2.5:在映射点的最大值和最小值中随机取数记为v;
步骤2.6:重复步骤2.1—2.5,直至采样数据小于最小分裂数值。
步骤3:计算每棵树的异常分数。
步骤3.1:输入x——待检测样本;T——孤立树;
步骤3.2:计算x映射在该分裂节点的最佳超平面上的值y;
步骤3.3:判断y是否大于0,若大于0则放在左子节点,若小于0则放在右子节点;
步骤3.4:重复步骤3.2—3.3,直至x落在的叶子节点的大小是一个外部节点;
步骤3.5:计算叶子节点与其直系父节点的数据质量;
步骤3.6:计算si(x)。
步骤4:遍历所有孤立树,计算异常分数的均值。
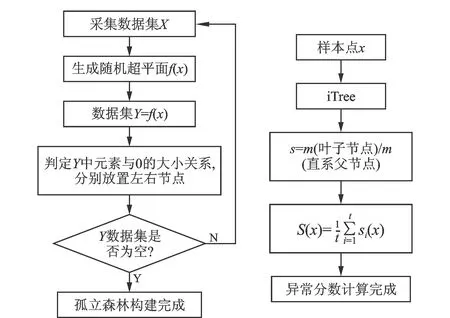
图2 改进的孤立森林算法流程Fig.2 Flow chart of the improved isolated forest algorithm
2 实验设计
为了验证改进的孤立森林算法以及该算法在催化裂化装置排污数据集的有效性,首先,基于标准异常检测数据集(见表1前3行)[23]对改进的孤立森林算法进行测试,并与经典的孤立森林算法、SCiForest、ReMa-iForest进行对比;其次,分别采用这几种方法对催化裂化装置排污数据进行异常识别,并对其结果进行分析。
本文采用的催化裂化装置排污数据集为我国某石油炼化企业350万吨/年重油催化裂化装置在2015年2月至2018年6月监测的氮氧化物浓度值。可能造成异常数据的因素主要包括[24]:(1)系统误差:主要是由监测仪器设备自身存在的问题或者监测环境变化引起;(2)系统故障:监控平台故障、通讯设备故障、现场仪器故障等原因;(3)人为造假:数据监测、收集等人员出于某种目的根据数据规律修改数据;(4)污染源异常变动:由企业的生产过程发生改变或者污染物治理设施故障引起。

表1 数据集特征Tab.1 Features of data sets
一般而言,异常数据检测结果主要分为正常数据和异常数据,然而,由于需要采用模型进行预测,因此将预测结果分为真正类(TP,True Positive)、真异类(TN,True Negative)、假正类(FP,False Positive)、假异类(FN,Fulse Negative),总数据量为4者之和。模型评价主要考虑有效性与执行效率两个方面。模型有效性是对模型准确度的检测,是衡量模型最重要的指标,通过计算模型的ROC(Receiver Operating Characteristic)曲线与AUC(Area Under Curve)值进行分析判断。在ROC 曲线中,横、纵坐标分别为假正比例
(7)
和真正比例
(8)
其中,VTPR为预测结果中正类数据的准确率,即真正类占所有正类的比;VFPR为预测结果中正类数据的错误率,即假正类占所有异类的比。由式(7)—(8)可以看出,VTPR越高VFPR越低,则模型性能越优秀。体现在ROC曲线上,则是曲线越陡峭、越靠近图片的左上方,模型效果越好。
SAUC的含义是ROC曲线下的面积,其值域为[0.0,1.0],模型的SAUC越接近1,则说明该模型的性能越好。
(9)
式中:na为真异类的个数;nn为真正类的个数;S为降序排列所有检测值的异常分数值中真异类的排序数值总和。
评价算法的执行效率首先要分析各个算法时间复杂度的理论值,然后在同一软硬件配置环境下执行算法,根据运行时间对算法的执行效率进行定量评价。
3 结果与分析
3.1 有效性分析
首先采用标准数据集Shuttle、Satellite与Annthyroid,对改进的孤立森林算法、孤立森林算法、SCiForest和ReMa-iFoest进行有效性分析。不同算法在不同标准数据集上的ROC曲线如图3所示。从图3可以看出,4种算法均能较好地识别标准数据集中的异常数据,但经改进的孤立森林算法的ROC曲线更靠近图的左上方,在4种算法中效果最好,这是由于本文改进的孤立森林算法结合分裂准则与相对质量方法,使其结果更优。
采用AUC值定量评价模型效果,从而直观地表示模型的优劣。模型在标准数据集上计算的AUC值见表2(前3行)。由表2可知,本文所提出的改进的孤立森林算法在3个标准数据集上的异常检测准确度均高于其他3种算法,这主要是因为改进的算法在树模型的建立中引入了最优超平面,一方面能够考虑数据点的多维属性,提高了树模型的精度;另一方面最优的超平面能够最大程度地将一组数据点分割成两组离散度最小的数据集,将掩盖在正常数据下的局部离群数据有效地孤立出来。在数据点遍历孤立树的过程中,采用相对质量的算法计算异常分数,利用了异常点少而特殊的特点,在数据中过早被孤立出来的数据则拥有越小的相对质量。利用相对质量来计算异常分数,能够更直观地找到隐藏在全局正常数据中的异常数据点。
综合分析表1、表2可以看出,对于不存在局部异常数据的Shuttle数据集来说,4种算法在该数据上的表现都能达到0.99以上,这是由于孤立森林算法在处理大数据集上表现优秀,其建立的树模型能够快速、准确地对数据点进行分类。然而,对于另外3种数据集,孤立森林算法自身的缺陷就暴露出来。由于算法在前期的树模型构建过程中用到的子样本是通过对原始样本集随机采样而来,并且在异常分数检测过程中,根据路径来计算异常程度,这两者都导致在异常检测时,局部数据中表现异常的数据被放到全局来观测而很可能被误判为正常。对于数据中存在局部异常数据点但数据属性较少的数据集Satellite来说,改进的孤立森林算法的AUC值略高于其他3种算法。对于数据中存在局部异常数据点但数据属性较多的数据集Annthyroid来说,改进的孤立森林算法的AUC值明显高于其他算法,这是由于改进的孤立森林算法能够在检测局部异常数据点的同时考虑数据点的多种属性,提高了模型的检测精度。
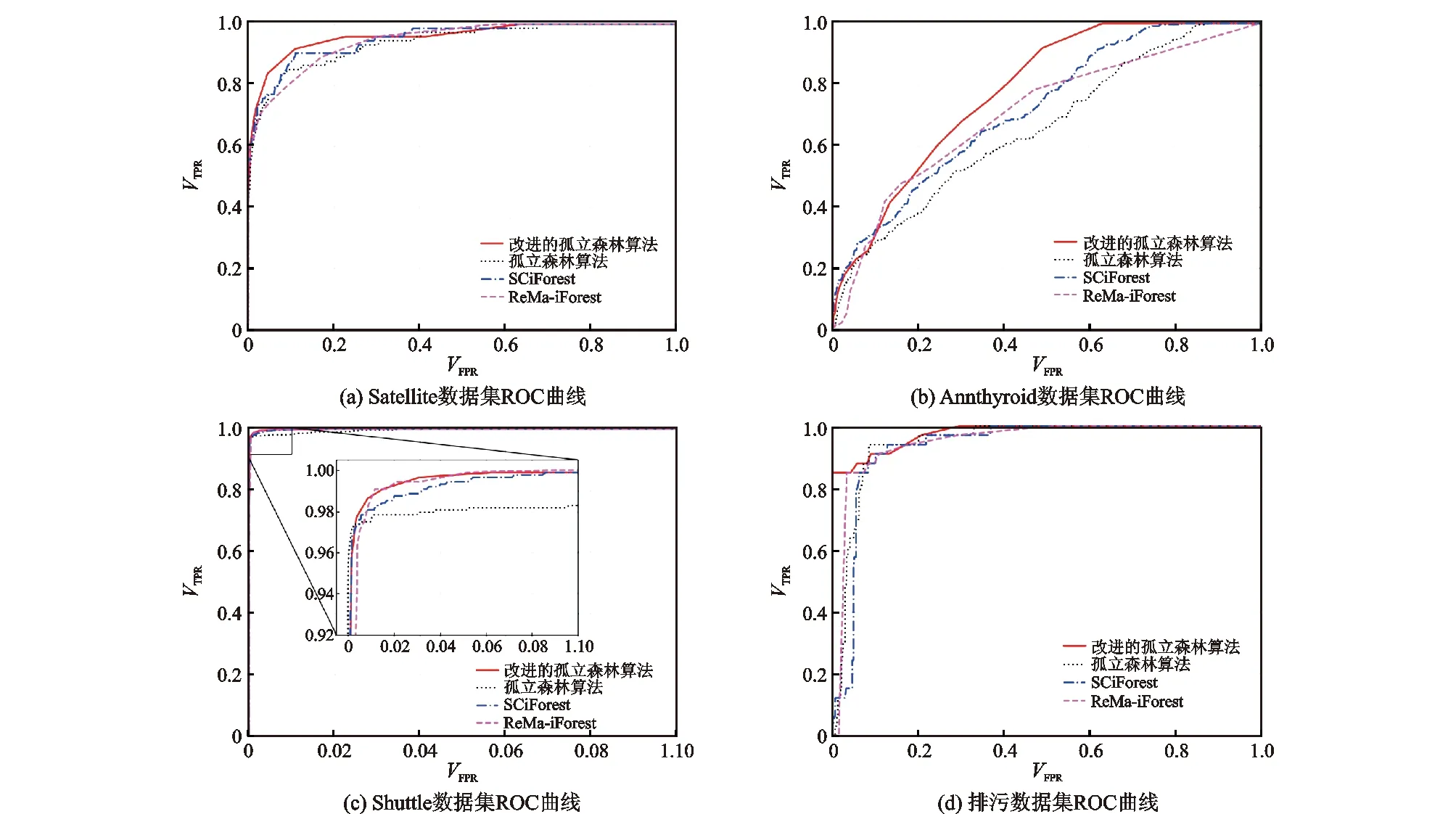
图3 不同算法在不同数据集上的ROC曲线Fig.3 ROC curves of different algorithms on different data sets

表2 不同算法在不同数据集上的AUC值Tab.2 AUC values of different algorithms on different data sets
3.2 执行效率分析
采用程序的运行时间评价改进的孤立森林算法、孤立森林算法、SCiForest及ReMa-iForest的执行效率。不同的算法在不同数据集上的运行时间见表3。

表3 不同算法在不同数据集的运行时间Tab.3 Time consumption of different algorithms on different data sets单位:s
从表3可以看出,ReMa-iForest 算法的运行时间明显低于改进的孤立森林算法、孤立森林算法及SCiForest。这是由于ReMa-iForest 没有通过计算叶子节点与根结点的平均距离来计算异常分数,而是根据数据所在的叶子节点的相对质量数来计算。同时,ReMa-iForest 树模型建立过程中,叶子节点数小于5 即可结束树的建立,这样既减少了树模型的高度也减少了遍历树所用的时间。而SCiForest的运行时间较其他3种算法来说都偏长,这是由于SCiForest 不仅在分裂节点添加了随机超平面,还需要对随机超平面进行判断选出最优超平面,同时在数据点遍历过程中,数据点需要先映射到超平面上再进行判断,这一做法虽然有效提高了模型的精度,但却降低了模型的执行效率。本文提出的改进孤立森林算法综合了SCiForest与ReMa-iForest的优点,中和了二者的缺点,因此其计算时间介于两者之间,既兼顾了算法的异常识别精度,又平衡了算法的执行效率。
经过理论分析可知,孤立森林算法在训练过程中训练t棵树的时间复杂度为O(t(n+φ)log2(ψ)),测试阶段测试n个数据点的时间复杂度为O(ntlog2(φ));SCiForest算法在训练过程中的时间复杂度为O(tτφ(qφ+log2(φ)+φ),测试阶段的时间复杂度为O(qnφt);ReMa-iForest算法在训练过程中的时间复杂度为O(t(n+φ)log2(φ)),测试阶段的时间复杂度为O(ntlog2(φ));改进的孤立森林算法在训练过程中的时间复杂度为O(tτφ(qφ+log2(φ)+φ)),测试阶段的时间复杂度为O(ntlog2(φ))。从时间复杂度上来看,从小到大排序为:ReMa-iForest、孤立森林、改进的孤立森林、SCiForest算法。
3.3 催化裂化装置排污数据集异常检测
经过有效性分析与算法执行效率分析之后,本文采用改进的孤立森林算法、孤立森林算法、SCiForest及ReMa-iForest对催化裂化装置排污数据集进行了异常值检测。数据测试集共包含500个数据样本,30个异常数据样本,470个正常数据样本;模型阈值设置为0.12。4种算法在催化裂化装置排污数据集上的ROC曲线见图3(d),AUC值见表2(第4行)。由图3(d)可以看出,4种算法在催化裂化装置排污数据集上表现较好,ROC曲线均位于图的左上角,仔细观察可以发现改进的孤立森林方法的ROC曲线更加陡峭,结合表2中的AUC值可以看出,改进的孤立森林算法的识别效果在4种算法中表现最优。改进的孤立森林算法在催化裂化装置排污数据集上检测出异常数据31个,其中真异数据29个,假异数据2个,异常数据识别效果如图4所示。图4(a)为模型的识别效果,即模型在数据集中检测出的异常数据与真正异常数据的分布关系。图4(b)为异常检测模型的检测效果,即模型检测出的异常数据中真异值与假异值的分布关系。经计算可知,模型在排污数据测试集上的异常数据识别率为96.66%(即模型检测的真异数据占总体异常数据的比),异常数据检测准确率为93.54%(即模型检测的异常数据中真异数据的占比)。

图4 催化裂化装置排污数据异常识别效果Fig.4 Detection results of anomaly data in pollution emission data of FCCU
4 结束语
数据异常识别是数据分析中不可或缺的重要环节。本文对孤立森林算法进行了深入研究,结合了分裂准则与相对质量对孤立森林算法进行了改进。采用标准数据集(Shuttle、Satellite、Annthyroid)对算法的异常识别效果进行了有效性分析,并与常见的异常数据识别算法(经典的孤立森林方法、SCiForest、ReMa-iForest)进行了对比。采用改进的孤立森林算法对催化裂化装置外排污染数据集进行了异常识别,对算法的有效性与执行效率进行了分析,结果表明,无论在标准数据集还是催化裂化装置排污数据集,改进的孤立森林算法均能在提高模型精确度的同时提高算法的执行效率。本研究工作将为催化裂化装置外排污染数据的异常识别方法提供有益参考,为后续的数据分析与处理提供数据支撑,为促进炼化企业污染物外排稳定达标提供数据保障。

