差分进化变异策略rand/3/bin求解0-1背包问题∗

王泽旭文 斌罗自强

（1.数据科学与智慧教育教育部重点实验室（海南师范大学）海口571158）

（2.海南师范大学云计算与大数据研究中心 海口571158）（3.海南师范大学信息科学技术学院 海口571158）

1 引言

0-1背包问题（Knapsack problem）的定义为在给定背包容量的情况下实现背包的总价值最大化问题，抽象为数学概念就是一个组合优化的完全NP问题［10］。0-1背包问题有着非常广泛的实际应用。在组合数学、应用数学、密码学等领域经常将问题抽象为0-1背包问题来研究和解决。

解决0-1背包问题的方法主要分为两大类：最优算法和启发式的算法。最优算法主要包括动态规划、贪婪算法、回溯法等；启发式算法包括遗传算法、差分进化算法、粒子群算法等主要以仿自然算法为主。最优算法虽然可以解出函数的最优解，但是比较局限于处理小规模的问题求解。启发式算法［8］更适合大规模的运算求解，这类算法主要以仿自然体算法为主，适用于求解全局最优值，但是由于超级个体、变异概率、交叉概率等因子选择不恰当会导致早熟或者收敛过慢等问题。

本文通过结合差分进化算法不同变异策略的特点，提出一种新的解决离散型0-1背包问题的变异策略（rand/3/bin），该策略解决了一般的差分进化算法在收敛前期缺少多样性收敛过快导致早熟，收敛后期收敛速度过慢的等问题。

2 0-1背包问题的数学模型如下

每一件商品都拥有其自己的重量wi、价值pi，共有n件商品，若有一个容量为R的背包载荷，需要考虑如何分配使得商品的总重量在不超过最大容量的前提下，使得商品的总价值最大［8］。即当商品i被选中时，对应的xi为1，否则为0。因此，实际背包的总重量为商品的总价值为其函数模型如下：

式中xi取0或1，i=1，2，…，n，n，c均为正值。

3 基本差分进化算法

将由前一代个体之间的变异产生的变异个体，以一定的概率将变异个体与前一代个体进行交叉实验，生成实验个体。根据适应的的大小，在前一代个体与实验个体进行贪婪选择，将比较优良的个体保留，实现进化的目的［11］。

对于D维的空间维度，当规模为NP的种群，进化到第t代时，种群表示为其中某一个个体用来表示。在进化过程中，对于每个都会进行变异、交叉和选择的操作。

3.1 变异操作

3.2 交叉操作

3.3 选择操作

差分进化算法采用的是“贪婪”选择策略［1］，从前一代和试验个体中进行贪婪选择，选择其中适应度值最好的个体作为下一代，表达式如下：

其中，fitness(·)为适应度函数，在选取适应度函数时一般选择目标函数。本次实验选取目标函数为适应度函数并求取函数极小值。

4 对于0-1背包问题改进的离散差分进化算法

本文通过结合多种变异策略在搜索过程中不同阶段的特点以及在搜索过程中勘测能力与开发能力需求的变化，提出一种基于新的变异策略rand/3/bin的改进差分进化算法。

4.1 基于变异策略rand/3/bin的差分进化算法简介

变异策略rand/3/bin是根据在搜索的过程中前半阶段要求开发能力较强，后半阶段收敛能力较强的动态需求变化，提出的一种新的变异策略。使得算法在快速收敛的同时，避免早熟陷入局部最优。要取得全局最优的结果就要保证在搜索的前期保证个体的多样性，后期拥有较强的收敛速度。

在变异策略rand/3/bin中，使用以下方法产生新的变异个体：

4.2 改进差分进化算法的基本步骤

1）对参数进行初始化：种群规模NP；缩放因子F；变异因子CR；空间维数D；进化代数t=0；

3）对个体进行评价：通过计算适应度值，对个体进行评价。

4）变异：按如下所示rand/3/bin策略对每个个体进行变异操作，并得到变异个体

5）交叉：按式（2）对每个个体进行交叉操作，得到试验个体

5 实验

在利用差分进化算法进行0-1背包实验时发现，变异策略为rand/1/bin和rand/2/bin的实验结果较稳定，使用其他变异策略的差分进化算法并不适合解决0-1背包的离散型问题，因此，本实验的加入编译策略为rand/1/bin和rand/2/bin差分进化算法。

本次实验使用10个典型的0-1型背包测试数据进行试验（测试数据：https：//github.com/woods 1060/0-1knapsack-data.git），并通过将两种不同的变异策略的差分进化算法、遗传算法、粒子群算法做仿真对比实验，验证使rand/3/bin变异策略的改进的差分进化算法的有效性。

在仿真对比实验中将改进的差分进化算法与遗传算法、粒子群算法以及两种基本的差分进化算法（采用rand/1/bin，rand/2/bin变异策略）进行对比分析研究。在改进算法的实验中，设定参数F0=0.95，CR=0.8，其他算法中的参数设置选择文献推荐值。为了在公平的仿真环境下测试各个算法的性能，分别对每个测试数据每个算法进行30次的独立运行。表1总结了各个算法在不同测试数据上所得到的仿真结果，表中的real value表示测试的最优值，best表示最好的实验结果，mean表示30次实验的平均值，std表示标准差，t表示时间单位为s。为了方便清晰地观察实验结果，用粗体表示各实验测试的最佳结果。图1绘制了基于最优值的收敛曲线，与表1不同，这些收敛曲线可以提供收敛性，稳定性等多种信息。

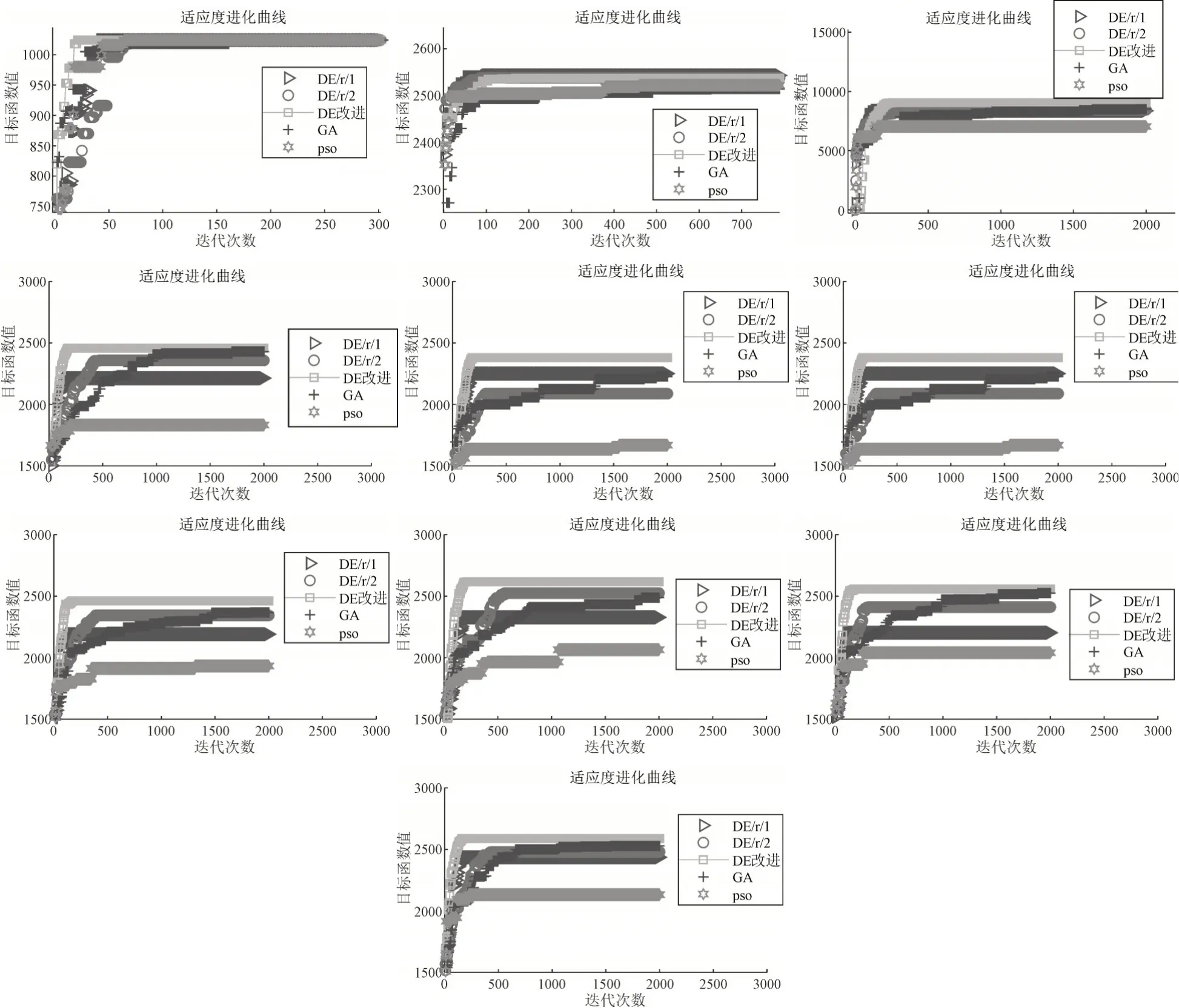
图1 各算法的测试收敛曲线

表1 各算法实验结果对比

由图表分析可得，遗传算法、差分进化算法、粒子群算法三种算法相比较而言，遗传算法的实验结果更能逼近实验的最优值，但是需要更多的实验迭代次数达到最优值；粒子群算法实验结果相对较差，收敛速度中等；差分进化算法的实验结果在逼近实验最优值的同时，收敛速度很快，标准差较小，稳定性强，比较适合解决0-1背包问题。

变异策略DE/rand/2/bin获得实验值大部分情况下接近于真实值，但是其需要迭代的次数非常多；变异策略DE/rand/1/bin收敛速度比较快，但是在实验值中得到的实验结果并不是很稳定；变异策略DE/rand/3/bin改进算法在快速收敛的同时获得实验结果最为接近最优值。

对于变异策略DE/rand/2/bin，利于保持种群的多样性容易获得最优值，但是它的收敛速度过慢，局部搜索能力较差；变异策略DE/rand/1/bin，局部搜索能力较强，收敛比较快，但是不利于获得多样性的种群，得到的实验值不能很好地靠近最优值；变异策略DE/rand/3/bin结合了rand/1保持种群能够多样性和rand/2局部搜索能力较强的特点，实现搜索前半期增强种群多样性，后半阶段增强局部搜索的能力，从而达到实验优化的结果。由实验数据可得，使用新的变异策略的差分进化算法在处理大规模的0-1背包问题时，拥有显著的优越性。

6 结语

本文对于离散型0-1背包问题提出了一种基于新的变异策略rand/3/bin的差分进化算法，并通过实际算例验证了新变异策略的可行性与有效性。使用该变异策略的算法实现过程简单，实验结果良好，算法稳定，拥有较强的勘测能力与开发能力，非常适合用于大规模的0-1型背包运算。