基于不确定语言区间直觉模糊Choquet积分的决策方法研究

王红娟

(内江师范学院，四川 内江 641100)

1 引言

决策方法是经过专家对方案的属性进行评价然后通过聚合算子聚合决策信息最终从有限个方案里选出最优方案的过程，近年来受到越来越多的关注[1～3]。企业可以通过决策方法从几家供应商中选最好的一家。因为决策问题的模糊性，专家难以通过一个精确的数来刻画决策问题的不确定性。因此，模糊集是一个很好的选择，直觉模糊集被提出[4]。Atanassov等[5]介绍了区间直觉模糊集，通过隶属度和非隶属度来描述满意度和不满意度，它比直觉模糊集能够更好地刻画决策问题的模糊性，因为专家对属性评价的满意度和不满意度是用区间来表示。因此区间直觉模糊集受到许多学者的关注[6，7]。

在实际决策问题中，等级值可以用其他种类的变量，比如语言变量。语言表达要更符合专家的评价考虑并且更容易提供比直觉模糊集，比如专家要评价某种用品的质量，可以直接给出一些语言术语，如“好”“中等”“差”来表示评估值。Zadeh[8～10]提出了语言变量的定义并且提出了决策方法基于语言变量。Chen等[11]将直觉模糊集推广到了语言直觉模糊集，它的隶属度和非隶属度都是语言变量。 为了进一步提高语言直觉模糊集的描述性，Garg等[12]介绍了语言区间直觉模糊集，隶属度和非隶属度用语言变量的区间来表示。许多学者提出了关于语言区间直觉模糊集的算子，Qin等[13]介绍了语言区间直觉模糊Archimedean power Muirhead均值(LIVIFAPMM)和语言区间直觉模糊Archimedean 加权power Muirhead均值(LIVIFAWPMM)。为了更好地描述决策问题中的不确定性，Xu[14]介绍了不确定语言变量的定义。此后，在不确定语言环境之下多属性决策方法受到了广泛关注并且得到了不同的语言集，如毕达哥拉斯不确定集[15]，区间毕达哥拉斯不确定集[16]。

聚合算子对决策方法是一种非常有用和重要的工具。Choquet积分在决策问题中是聚合决策信息非常有用的工具，可以考虑决策问题中属性的重要性和属性间的关联通过模糊测度。因此，Choquet积分在模糊环境中应用非常广泛[17，18]。

根据语言区直觉模糊，为了能够更好地刻画决策问题的不确定性和模糊性，属性的重要性和相互关联，本文提出不确定语言区间直觉模糊Choquet积分平均(ULIVIFCA)算子和不确定语言区间直觉模糊Choquet积分几何(ULIVIFCG)算子。

本文主要由以下几部分构成： 首先给出基本概念，如区间直觉模糊集、不确定变量、模糊测度和Choquet积分等的概念； 然后给出不确定区间直觉模糊集的定义和比较不确定区间直觉模糊数大小的方法；其次给出ULIVIFCA和ULIVIFCG，且分别介绍这两个算子的性质；再次介绍了一个多属性群决策方法基于ULIVIFCA和ULIVIFCG在不确定区间直觉模糊的环境中，并且运用介绍的方法在实例中，最终选出一个最优的方案且说明介绍的方法的实用性。

2 基础知识

2.1 区间直觉模糊集和不确定变量

定义1[6]假设Χ是一个给定的集合，则区间直觉模糊集定义为：

y={〈x,[ζL(x),ζU(x)],[ϑL(x),ϑU(x)]〉|x∈Χ}

其中[ζL(x),ζU(x)]⊆[0,1],[ϑL(x),ϑU(x)]⊆[0,1]满足0≤ζU(x)+ϑU(x)≤1。

假设S={st|t=0，…,l}是一个基数为基数的语言项集，其中st表示语言变量的可能值。例如下面集合:

S={s0=很差，s1=比较差，s2=中等，s3=比较好，s4=很好}。

语言集满足下面的特征：

(1)sk≥st当且仅当k≥t；

(2)否定算子：neg(sk)=st使得t=1-k;

(3)最大算子：max(sk,st)=sk，如果sk≥st;

(4)最小算子：min(sk,st)=sk，如果sk≤st。

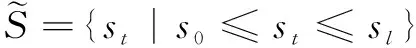
2.2 模糊测度和Choquet积分

Sugeno[20]介绍了模糊测度，Choquet积分可以来表示决策属性的重要性通过模糊测度。下面将介绍模糊测度和Choquet积分。

定义3[20]如果Χ是一个给定集合，P(Χ)是Χ的幂集， 函数χ:P(Χ)→[0,1]叫做Χ上的模糊测度，满足两个条件：

(1)χ(Φ)=0,χ(Χ)=1;

(2)满足ε,F∈P(Χ)和ε⊆F,则χ(ε)≤χ(F)。

Sugeno[20]定义了κ模糊测度， 因为用上面定义难以计算模糊测度。

χ(ε∪F)=χ(ε)+χ(F)+κχ(ε)χ(F),

其中ε∩F=Φ参数κ∈[-1,+∞]表示元素之间的关联。

如果Χ是有限的，则κ-模糊测度满足：

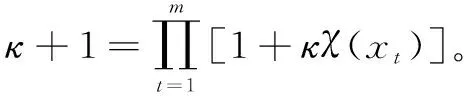
此外，对于任意ε∈P(Χ),有

设Χ是一个有限集合，元素xt(1≤t≤m)满足0<χ(xt)<1,则存在唯一的κ∈(-1,∞),κ≠0满足(3)[21]。

定义4[22]设Χ是一个给定集合,函数y:Χ→R+，χ是Χ上的模糊测度，Choquet积分为：

其中(1),…,(n)为(1,…,n)的一个排列满足y(x(n))≥…≥y(x(1)),

Ψ(t)={x(t),x(t+1),…,x(n)},并且Ψ(n+1)=Φ。

3 不确定语言区间直接模糊集

下面将给出不确定语言区间直接模糊集的概念。

定义5 假设Χ是一个给定的集合，Χ上的不确定语言区间直觉模糊集X表示为：

X={〈x,[sζL(x),SζU(x)],[sϑL(x),SϑU(x)]〉x∈Χ},

下面介绍不确定语言区间直觉模糊数的运算，ϖ=([se,sf],[sg,sh]),

ϖ1=([se1,sf1],[sg1,sh1]),

ϖ2=([se2,sf2],[sg2,sh2]),：

t>0,

t>0,

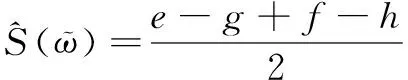
设ϖ1=([se1,sf1],[sg1,sh1])，

ϖ2=([se2,sf2],[sg2,sh2])则

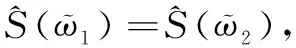
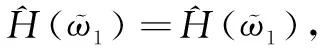
4 不确定语言区间直觉模糊Choquet积分

下面介绍不确定语言区间直觉模糊Choquet积分平均(ULIVIFCA)和不确定语言区间直觉模糊Choquet积分几何(ULIVIFCG)。

定义6 设ϖt=([set,sft],[sgt,sht])(t=1,…,m)， 如果

ULIVIFCA(ϖ1,…,ϖm)=

则称ULIVIFCA为不确定语言区间直觉模糊Choquet积分平均算子。

例1 设ϖ1=([s3,s4],[s2,s3])，ϖ2=([s4,s5],[s3,s3])和ϖ1=([s3,s5],[s2,s2]),

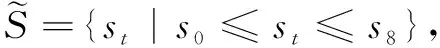
下面是ULIVIFCA的几个性质：

(1)幂等性:对于任意的t，如果ϖt=ϖ，则ULIVIFCA(ϖ1,…,ϖm)=ϖ。

(2)有界性:设ϖt=([set,sft],[sgt,sht])(t=1,…,m)，则min{ϖ1,…,ϖm}≤ULIVIFCA(ϖ1,…,ϖm)≤max{ϖ1,…,ϖm}。

定义7 设ϖt=([set,sft],[sgt,sht])(t=1,…,m)， 如果

ULIVIFCA(ϖ1,…,ϖm)=

则称ULIVIFCG为不确定语言区间直觉模糊Choquet积分几何算子。

例2 设ϖ1=([s3,s4],[s2,s3])，ϖ2=([s4,s5],[s3,s3])和ϖ1=([s3,s5],[s2,s2]),

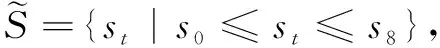
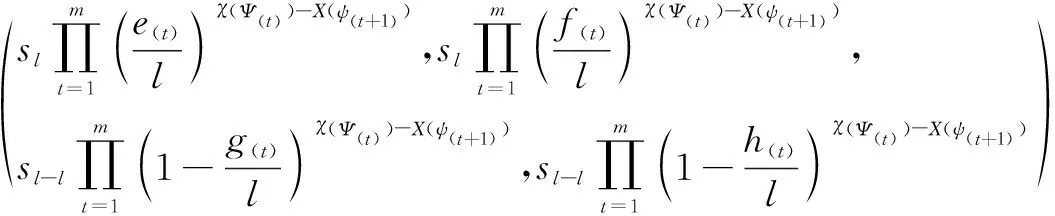
下面是ULIVIFCG的几个性质：

(1)幂等性: 对于任意的t，如果ϖt=ϖ，则ULIVIFCA(ϖ1,…,ϖm)=ϖ。

(2)有界性:设ϖt=([set,sft],[sgt,sht])(t=1,…,m)，则min{ϖ1,…,ϖm}≤ULIVIFCA(ϖ1,…,ϖm)≤max{ϖ1,…,ϖm}。

5 决策方法

群决策方法是从几种方案里选最优方案，下面介绍一种新的多属性群决策方法。首先介绍多属性群决策方法的模型。

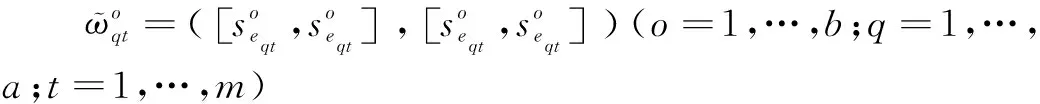
步骤2：分别建立专家和属性集的模糊测度；

步骤3：对矩阵里的不确定语言区间直觉模糊数进行排序；

步骤5：对矩阵Λ=(ϖqt)a×m里的不确定语言区间直觉模糊数进行排序；

步骤6：分别用ULIVIFCA和ULIVIFCG对Λ=(ϖqt)a×m进行聚合，得到ϖq=(q=1,…,a)；

步骤7：计算得分值和精确值, 选出最优方案。

例：某企业为了更高效地生产产品，根据专家的评价要从Α1,Α2,Α3这3家供应商里选一家来提供原材料，三位专家Β1,Β2,Β3对这3家供应商的原材料成本(С1)、原材料质量(С2)和风险因素(С3)用不确定语言区间直觉模糊数ϖ=([se,sf],[sg,sh])进行评价[se,sf],[sg,sh]⊆[s0,s8]，专家对三家供应商的评价结果，如表1。

表1 矩阵

步骤1：分别建立专家和属性集的模糊测度；

令χ({Β1})=0.4,χ({Β2})=0.35,χ({Β3})

=0.35,则

Χ({Β1,Β2})=0.71,Χ({Β1,Β3})=0.71,Χ({Β2,Β3})=0.67,Χ({Β1,Β2,Β3})=1;

令χ({С1})=0.3,χ({С2})=0.3,χ({С3})

=0.35,则

χ({С1,С2})=0.61,χ({С1,С3})=0.67,

χ({С2,С3})=0.67,χ({С1,С2,С3})=1。

步骤2：对矩阵里的不确定语言区间直觉模糊数进行排序；

步骤3： 分别用ULIVIFCA和ULIVIFCG对排序后的不确定语言区间直觉模糊数进行聚合，得到矩阵Λ=(ϖqt)a×m，表2、3；

步骤4：对矩阵Λ=(ϖqt)a×m里的不确定语言区间直觉模糊数进行排序；

步骤5：分别用ULIVIFCA和ULIVIFCG对排序后的不确定语言区间直觉模糊数进行聚合，得到ϖq(q=1,…,3)；

ϖ1=([s3.446,s4.267],[s1.404,s2.337]),

ϖ2=([s3.111,s4.638],[s1.255,s2.475]),

ϖ3=([s3.377,s4.779],[s1.807,s2.610]);

ϖ1=([s3.280,s4.171],[s1.482,s2.459]),

ϖ2=([s2.876,s4.523],[s1.312,s2.542]),

ϖ3=([s3.072,s4.657],[s2.035,s2.774])。

表2 矩阵(ULIVIFCA)

表3 矩阵(ULIVIFCA)

对上面结果分别计算得分值：

S(ϖ1)=1.987,S(ϖ2)=2.010,S(ϖ3)=1.869;

S(ϖ1)=1.755;S(ϖ2)=1.773,S(ϖ3)=1.460。

分别用ULIVIFCA和ULIVIFCG算子得到3家供应商的排序都是Α3<Α1<Α2，可见Α2是最优的一种方案，该企业可以和供应商Α2合作提供原材料。在多属性决策问题中，属性之间存在关联，通过集成Choquet积分和不确定语言区间直觉模糊数，介绍的方法可以考虑属性之间的关联属性的重要性通过模糊测度，并且不确定语言区间直觉模糊数能够很好地描述决策中的不确定性。

6 结语

本文首先介绍了不确定语言区间直觉模糊数，根据不确定语言区间直觉模糊数和Choquet积分介绍了不确定语言区间直觉模糊Choquet积分平均和不确定语言区间直觉模糊Choquet积分几何，不确定语言区间直觉模糊集比语言集能更好的描述决策问题中的不确定性和模糊性，Choquet积分能够刻画属性间的关联和属性的重要性通过模糊测度。并且介绍了比较不确定语言区间直觉模糊数大小的方法，还介绍了ULIVIFCA和ULIVIFCG各自的幂等性和有界性。最后介绍了多属性群决策方法并且应用到供应商的选择中，最终选出最优的一家供应商， 此实例也说明所介绍的多属性群决策方法的实用性。接下来的工作可以将不确定语言区间直觉模糊数和其他算子结合，语言变量要更容易提高评价值。