高频雷达检测海面慢速目标的优化MVDR 法*
滕文媛,张玉欣
(1.吉林铁道职业技术学院,吉林 吉林 132200;2.北华大学电气与信息工程学院,吉林 吉林 132013)
0 引言
在天波超视距雷达(Over the Horizon Radar,OTHR)进行海面探测时,由于舰船等目标的速度较慢,其多普勒频率与能量强大的海杂波很接近,海杂波的多普勒频率区间的典型值为1.5 Hz[1-2],要在如此狭窄的频率区间内识别出慢速舰船目标本身就比较困难,再加上OTHR 电磁波传播时经常受到不稳定电离层多径调制和相位路径非线性变化的影响[3],使得海杂波对应的多普勒谱线发生展宽,遮盖了与其邻近的弱小慢速目标,这样导致慢速目标的多普勒频率可检测区间更小,严重增加了舰船等慢速目标的检测难度。
对OTHR 而言,为了获得较好的舰船目标检测效果,必须提高回波数据的多普勒分辨率,在常规的基于傅里叶变换(Fast Fourier Transform,FFT)的多普勒谱分析模式下,频谱分辨率与相干积累时间有关,大致等于相干积累时间(Coherent Integration Time,CIT)的倒数[1]。采用长CIT 的工作方式可以增大回波数据的长度,提高频谱的多普勒分辨率,从而能够较容易地从海杂波背景中识别出舰船目标。但选择长CIT 也存在着两个弊端:一是增加了OTHR 在固定观测区域内的驻留时间,导致OTHR 对其他探测区域的重访频率降低,削弱了装备在实际工作中的大范围预警能力;二是在较长的CIT 内,电离层的不稳定特性会增大回波信号相位路径非线性变化的几率,直接引起海杂波谱展宽,即使采取了电离层信道选择措施,也不能完全消除它对回波的影响[4]。因此,为了保证OTHR 多方位、大范围的预警能力、提高区域重访率和降低电离层相位调制的影响,实现短CIT 条件下的慢速目标检测显得尤为重要。
目前,许多文献提出利用高分辨谱估计方法代替FFT 进行回波频谱分析[5-7],在回波数据较短的情况下即可发现目标。文献[8]将奇异值分解法(Singular Value Decomposition,SVD)与Tufts 和Kumaresan 提出的方法相结合,并根据Akaike 信息论准则,解决了自回归(Autoregressive,AR)模型阶数准确选择的问题,大大提高了多普勒频率分辨率。文献[9]对回波自相关矩阵进行了修正,改善了谱峰搜索性能,提出的改进MUSIC 谱估计法提高了多普勒频率的估计准确度。在众多的高分辨谱估计技术中,最小均方无失真响应(Minimum Variance Distortionless Response,MVDR)谱估计法属于非参数化的估计方法,与MUSIC 谱估计方法不同,MVDR 法不需要进行特征值分解,也不需要划分信号和噪声子空间,能够更有效地避免伪峰产生,但是MVDR法仍需要在频率区间进行遍历搜索,计算量较大。为解决该问题,本文基于最速下降原理给出了优化的MVDR 法,该方法先计算出最优的搜索步长,然后迭代进行谱线估计,相对于常规MVDR 法,优化方法大大缩短了搜索时间,并且谱峰的估计准确度有了较大提高。
1 海面回波模型和常规MVDR 谱估计法
高频超视距雷达一般采用调频连续波信号[10],海面探测回波经过脉冲压缩和匹配滤波处理后,其形式可以表示为

采用高分辨率谱估计法能够在数据长度较短的情况下,实现频率的高分辨分析,比FFT 分析的精度更高。其中,MVDR 的谱估计定义为[11]

2 优化的MVDR 法
令式(2)的分母为h(f),即
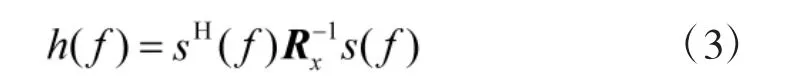
常规MVDR 法通过对频率区间进行遍历来获得谱峰最值,最终估计出的频率值的精确度与遍历步长有关,遍历步长越小,则精度越高,但弊端是计算量大、运算时间过长。为克服该问题,本文采用最速下降法[12]来搜索h(f)的局部极小值,定义搜索的迭代方式为

从式(3)和式(4)可以看出,当步长ξk选择为最佳值ξ 时,h(f)即可达到最小值,即
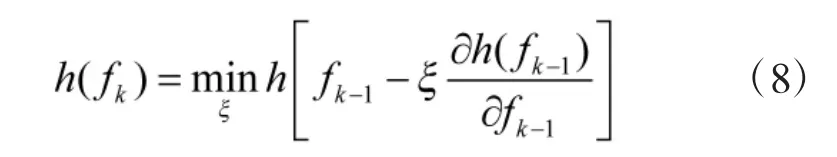
可见,如何计算出最佳的步长ξ 成为关键,下面将给出ξ 的计算方法。
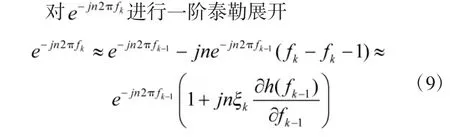
将上式代到s(fk),有

其中,I 是单位矩阵。把式(10)代入式(3),有

对式(11)求关于ξk的偏导数
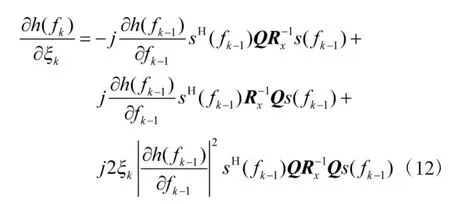
式(6)已经计算出了h(f)在f 处的梯度值,将其带入式(12)

显然,ξk的最佳值是在式(13)为0 时取得,则最佳步长ξk可通过下式进行计算
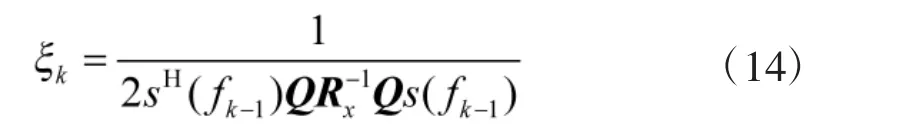
综合以上推导,基于最速下降的优化MVDR 谱估计方法的流程为:
Step 1:设置k=1,频率初值为f0;

Step 3:根据式(14),计算出最佳步长ξk;
Step 4:根据式(4),更新fk,k=k+1,返回Step 2继续迭代计算。
3 实验仿真分析
3.1 优化MVDR 法的舰船检测结果
OTHR 实验的仿真参数设置为:工作频率10 MHz,发射的电磁波信号为调频连续波信号;一个扫频周期持续250 ms,在每个扫频周期内采样100点数据;一个CIT 内发射64 个脉冲;设定探测区域内只有一个慢速舰船目标;正一阶海杂波峰杂噪比为30 dB,负一阶海杂波峰杂噪比为25 dB,二阶和高阶海杂波的杂噪比为5 dB。为模拟短数据回波情况,截取某距离单元回波数据的前16 点进行处理。
舰船目标的信噪比为0dB,多普勒频率为-0.8 Hz。分别采用MVDR 法和优化MVDR 法进行回波谱分析,其中:MVDR 法选择两种频率步长(0.02 Hz 和0.008 Hz)在-2 Hz~2 Hz 区间进行遍历搜索,处理结果如下页图1 所示。由图1 可见,当慢速舰船多普勒频率与海杂波峰较近时,MVDR 法和优化MVDR法都能较准确地估计出目标频率,当步长为0.02 Hz和0.008 Hz 时,常规MVDR 法分别检测出舰船目标多普勒频率为-0.765 Hz 和-0.77 Hz,而优化MVDR 法得到的舰船多普勒频率值为-0.794 Hz。常规MVDR 的估计精度随着搜索步长的减小而提高,但是即使步长减小到0.008 Hz(对应于500 个频率搜索点),MVDR 法的目标估计准确度也差于优化方法,若要提高MVDR 的估计精度,必须进一步减小搜索步长,但同时也必然导致运算量大大增加。

图1 谱估计方法的检测结果
3.2 方法的性能比较
OTHR 实验的仿真参数与3.1 节一致,仍然假设只有一个舰船目标;正一阶海杂波峰的杂噪比为30 dB,负一阶海杂波峰的杂噪比为25 dB,二阶和高阶海杂波的杂噪比为5 dB。
3.2.1 低信噪比下的分辨能力比较
设定舰船位于第40 个距离单元的回波数据中,多普勒频率为-1 Hz。分别采用MVDR 法和优化MVDR 法对每一个距离单元的数据进行回波谱分析,其中,常规MVDR 法仍然选择两种频率步长(0.02 Hz 和0.008 Hz)进行处理,分析结果如图2 所示。图2(a)~ 图2(c)分别给出了在低信噪比情况下,(-5 dB)3 种处理方式所得到的回波数据距离-多普勒谱。模拟结果表明,在相同低信噪比条件下,经过优化MVDR 法处理后,所得到达距离-多普勒谱图中目标峰值的准确度最好,其次是搜索步长为0.008 Hz 的MVDR 法,而搜索步长为0.02 Hz 的MVDR 法的估计准确度则是最低,究其原因是因为优化MVDR 法利用了最速下降原理,可以准确地找到目标峰值位置,而常规MVDR 法的准确度依赖于频率搜索步长,只有减小搜索步长,才能增大频率区间的搜索点数。
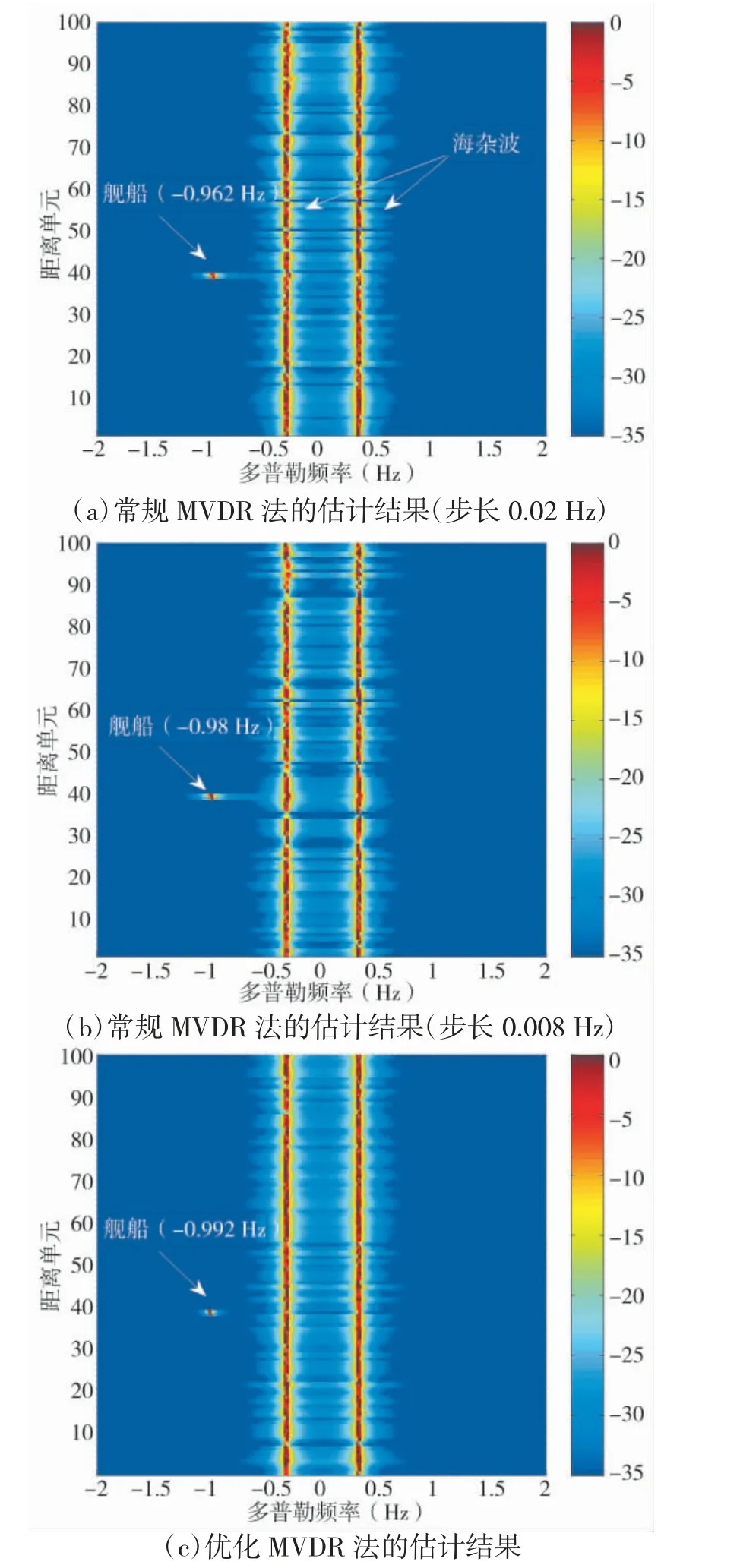
图2 低信噪比条件下的目标识别结果
3.2.2 目标峰值估计的均方误差比较
分析常规MVDR 法和优化MVDR 法在不同信噪比下的均方根误差的统计性能,常规MVDR 法的搜索步长仍然为0.02 Hz 和0.008 Hz。其他仿真参数同上,舰船目标的多普勒频率分别为-0.85 Hz 和-1.1 Hz,进行200 次Monte-Carlo 计算的统计结果如下页图3(-0.85 Hz)和图4(-1.1 Hz)所示。从图3和图4 可以看到,在信噪比较大的情况下,两种步长的MVDR 法的均方根误差相差不大,但优化MVDR 法的均方根误差明显小于前面二者;在信噪比较低时,步长为0.02 Hz 的MVDR 的均方根误差最大,步长为0.008 Hz 的MVDR 的均方根误差其次,优化MVDR 法的均方根误差最小,说明在不同信噪比条件下,优化MVDR 法的估计准确度都优于传统MVDR 法。

图3 不同信噪比下的均方根误差(-0.85 Hz)
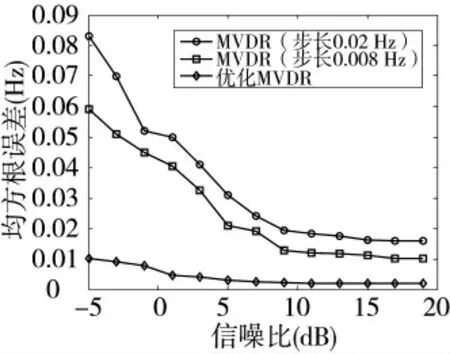
图4 不同信噪比下的均方根误差(-1.1 Hz)
通过上述实验,可以得出这样的结论:相对于传统MVDR 法,优化MVDR 法具有更高的多普勒分辨力、较低的信杂比门限和较小的估计均方根误差,可在低信噪比和目标多普勒频率靠近海杂波峰的条件下工作。
3.2.3 海态对目标检测结果的影响
海水的运动造就了海洋表面的波动,不同程度的海面波动对应于不同等级的海态。海态会对高频回波谱产生很大影响,在高等级海态下,会造成回波谱峰展宽和分裂。根据道格拉斯海态等级划分[13],海态共分为7 个等级,分别为:轻风(速度0~6 kn)对应1 级,微风(速度6 kn~12 kn)对应2 级,和风(速度12 kn~15 kn)对应3 级,大风(速度15 kn~20 kn)对应4 级,强风(速度20 kn~25 kn)对应5级,巨风(速度25 kn~30 kn)对应6 级,狂风(速度30 kn~50 kn)对应7 级。其中,kn 表示“节”,1 kn=0.514 8 m/s。不同等级的海态将会引入不同的回波测量误差,对目标检测结果产生影响。实验参数同3.1 节,改变海杂波模型中的风速因子,以此来评价不同方法的检测误差,均方根误差值通过取200 次Monte-Carlo 实验的均值获得。不同海态下,各种方法的检测误差如图5 所示。由图可见:当海态等级较低时(1 级,2 级),MVDR 法和优化MVDR 法均能较准确地检测出目标;当海态处于中等级时(3 级,4级),优化MVDR 法的误差明显小于MVDR 法,原因是:优化MVDR 法通过最速下降技术能够以优化路径逼近目标真值,避免了常规MVDR 法的网格搜索步骤,减小了搜索误差;当海态处于高等级时(5级~7 级),MVDR 法和优化MVDR 法的误差都很大,原因是:海态等级越高,海表面波动越剧烈,使得谱峰分裂的现象越明显,谱峰分裂会造成多个“伪目标”谱峰,结果会导致目标检测失败。针对高等级海态目标误判的问题,可考虑先利用相邻距离单元海杂波具有高度相关性的特点,采用子空间类方法[1]抑制海杂波,然后再利用高分辨率谱估计技术检测目标,该思路将在下一步工作中进行验证。

图5 不同海态等级下的检测误差
3.3 运算效率分析
由于OTHR 检测目标需要实时处理,检测方法的计算量对其实际应用具有很大的影响,本节对两种方法的计算效率进行比较,参数设置为:工作频率为12 MHz,扫频周期为250 ms,在每个扫频周期内采样100 点数据;一个CIT 内发射64 个脉冲;探测区域内只有一个多普勒频率为-0.8 Hz 的舰船目标;正一阶海杂波峰杂噪比为30 dB,负一阶海杂波峰杂噪比为20 dB,二阶和高阶海杂波的杂噪比为5 dB,截取某距离单元回波数据的前32 点进行处理;常规MVDR 法的搜索步长分别为0.004 Hz、0.005 Hz、0.008 Hz、0.02 Hz 和0.04 Hz,它们的处理时间分别对应图6 中的Ⅰ~Ⅴ,优化MVDR 法的处理时间对应图6 中的Ⅵ,各种方法的比较结果如图6 所示。从图6 可见,常规MVDR 法的运算时间与搜索步长成反比,搜索步长越小则运算时间越长,优化MVDR 法的运算时间远低于MVDR 法,甚至比步长为0.04 Hz 的MVDR 法的处理时间也要少0.58 s,说明优化MVDR 法在运算效率上也具有很大的优势。
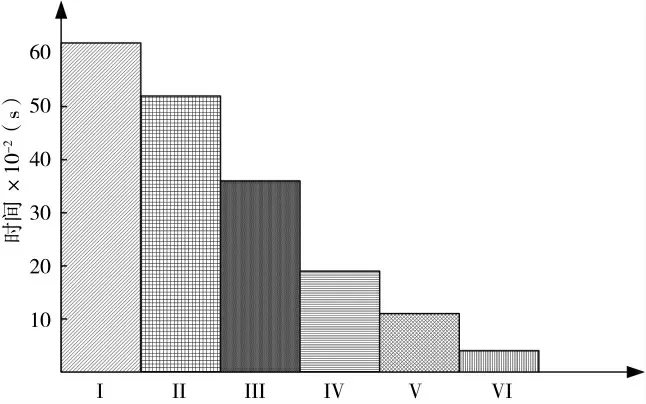
图6 各种方法的运算时间比较
4 结论
高频超视距雷达是进行海面探测和早期预警的重要装备,由于舰船目标的速度较慢,相对于飞机等快速目标来说,舰船目标的多普勒频率更靠近强大的海杂波,要从回波数据的杂波背景中识别出慢速舰船目标有较大难度。本文利用高分辨率谱估计法对短数据具有较高分辨率的特点,在常规MVDR 法的基础上结合最速下降搜索原理,提出了优化的MVDR 法。优化方法能够实现快速谱峰搜索,避免了对频率区间进行遍历网格式搜索,且谱峰估计精度更高,在低信噪比条件下也有良好性能。实验仿真结果验证了上述结论。
——中国制药企业十佳品牌

