基于多目标优化的航空器滑行速度曲线生成

唐博，韩松臣，梁斌斌,2

(1.四川大学空天科学与工程学院，成都 610065；2.四川川大智胜软件股份有限公司，成都 610045)

0 引言

2006年以来，全球民用航空运输量呈现出逐年增长[1]的趋势，我国的民航运输业务也在改革开放后进入了发展的快车道。民航运输业务的迅速发展使得机场场面交通运行压力日益增大，场面交通长期处于容量饱和的运行状态，这不仅导致航空器在地面运动过程中出现大量走走停停和排队的现象，并进一步产生了更多的燃油消耗和尾气排放，还使得管制员的工作压力也在增大，并开始影响航空器地面滑行安全。以中短程航空器A320为例，其在机场地面运动过程的燃油消耗占飞机总行程的5%-10%，其中滑行阶段约占10%-30%。据统计，大型机场若平均滑行时间降低5%，每年将减少400多万元人民币的油耗成本[2]。

缓解场面交通运行压力不仅需要扩建机场和跑道外，更多的需要更加科学高效的航空器路由规划方法。为此美国下一代空管系统NextGen和单一欧洲天空空中交通管理研究项目SESAR提出了将四维轨迹(4-Dimensional Trajectory，4DT)引入航空器地面运动过程中，接着美国国家航空航天局NASA正式提出了基于四维轨迹的场面运行概念(Surface Trajectory-Based Operations，STBO)[3]。航空器四维轨迹运行是在传统的滑行路径规划的基础上加入了时间条件，要求航空器在规定的时间内到达场面的特定位置并完成后续操作，通过实现基于完整四维轨迹的地面运动，可以最多减少55%的滑行延误时间[4]，并能有效提高航空器地面运动过程的可预测性。

航空器四维滑行轨迹由滑行路径和对应的滑行速度曲线构成，对于滑行路径规划和速度曲线生成国内外许多学者都从不同角度进行了研究，无论是在理论还是应用研究方面都取得了许多成果。Atkin等人[5]总结了2010年前的航空器地面运动的研究状况并指出了未来的研究方向，如将航空器地面运动和停机位分配、进离港/跑道排序问题整合，考虑对环境影响、考虑运动过程中的不确定因素和提升规划模型的鲁棒性等。Nikoleris等人[6]首次提出了利用ICAO引擎排放数据库[7]计算航空器油耗和污染物排放的方法。Ravizza等人[8]在Dijkstra算法的基础上提出了一种基于时间窗的快速路径规划算法QPPTW，能根据航空器的优先级次序依次为航空器规划滑行路径。Chen等人[9]2016年提出了主动路由(Active Routing，AR)的概念，其根据机场网络结构和航空器动力学模型优化滑行时间、油耗和污染物排放等多个目标，为航空器生成最优滑行路径和对应的滑行参考速度曲线，进而实现了航空器四维轨迹生成。周龙等人[10]提出采用DSW算法从历史数据中得到航空器滑行的标称速度剖面，然后结合BADA数据实现对部分瞬时速度的修正，最终得到航空器场面4D轨迹预测模型。Zhang等人[11]提出一种滑行速度在线生成方法，将速度生成问题建模为一个非线性优化模型，并提出了一种基于数学规划的启发式求解算法。Li等人[12]考虑了航空器大角度转弯对滑行时间的影响，并通过在遗传算法适应度函数中加入三种类型的冲突约束来实现航空器滑行路径的无冲突规划。

然而这些方法大多给定航空器一个基于经验的平均滑行速度，传统的基于平均滑行速度的路径规划方法不能准确地反映航空器滑行过程中速度的变化，而基于历史数据得到的标称速度剖面则会受航空器具体机型以及历史交互过程的影响，两种方法都不能较好反映航空器的实际滑行过程，会进一步导致预测场面各点到达时间出现偏差。因此，本文提出了一种高效的航空器四维滑行轨迹生成方法，建立了航空器分段线性滑行速度曲线模型，权衡了滑行时间、油耗和污染物排放目标之间的关系，同时提出了一种启发式搜索算法，用于生成一组航空器帕累托最优的滑行速度曲线。

1 航空器滑行速度曲线

1.1 滑行速度曲线模型

假设有航空器集合P={p1,p2,…,pn}，对于其中任意一架航空器pi，其滑行路径Ri可以通过一组节点序列Ri={ni,ni+1,…,ni+m}表示，m表示该条滑行路径对应的节点数量。由于直接生成完整的滑行速度曲线参数多、计算量高，因此先将航空器的整条滑行路径分段，通过求解每个滑行路段的最优速度曲线，再进行首尾连接，即可得到完整的最优滑行速度曲线。本文将完整的滑行路径分为：直线起始段、直线段、转弯段和直线停止段，其中转弯段定义为两个相邻的、航空器转向角大于30°的直线段之间的部分，转向角则可通过余弦定理求得。由于进港航空器最后停入停机位、离港航空器上跑道起飞前需要停止等待管制员指令，其滑行速度最终都会降为0，因此定义最后一个滑行路段为直线停止段。

以国内某机场一条滑行路径为例，其滑行路径分段示意图如图1所示，其中滑行路段(ni,ni+1)、(ni+2,ni+3)和(ni+4,ni+5)为直线段，(ni+1,ni+2)、(ni+3,ni+4和(ni+5,ni+6)为转弯段，(ni+6,ni+7)为直线停止段。

图1 滑行路径分段示意图

航空器滑行速度是一个与时间相关的连续函数，滑行速度会持续发生变化，难以建立速度和时间的精确函数。因此为了降低滑行速度曲线生成问题的复杂度，为航空器每一滑行路段建立分段线性滑行速度模型，如图2所示，共包括四个不同的滑行状态：加速、匀速、减速和急减速，对应航空器四种典型的运动状态。

图2 分段线性滑行速度曲线模型

在该速度曲线模型中，第一阶段为匀加速段，航空器以加速度a1从该段进入速度v0匀加速到v1，加速时间为t1，加速段路径长度为d1；第二阶段为匀速滑行段，航空器以速度v1滑行t2秒，滑行距离为d2；最后的减速段分为减速和急减速两个阶段，在减速段航空器先以加速度a3从v1减速到v3，减速时间为t3，减速段滑行的距离为d3，最后在急减速段航空器开始以最大加速度a4从v3减速到该段的脱离速度v4，减速时间为t4，急减速段滑行距离为d4。每个滑行路段的滑行速度曲线可由一组决策变量(a1,d1,d2,d4)唯一确定。

1.2 航空器滑行时间、油耗和污染物排放模型

滑行速度曲线模型中，每个滑行路段的速度曲线包含加速、匀速、减速和急减速四种运动状态，不同滑行状态对应航空器不同的推力等级。假设航空器发动机能产生的最大推力为F0，则根据文献[1]，航空器在地面滑行过程中匀速阶段的推力等级ε=5.2%F0，转弯阶段ε=7%F0，减速阶段ε=5%F0，怠速阶段ε=4%F0，则可进一步利用ICAO引擎排放数据库中提供的其他推力等级下的油耗速率和污染物排放指数，通过曲线拟合求得速度曲线模型中每个运动状态的油耗速率fk和污染物排放指数ek，因此航空器滑行路段j的滑行时间TTj可以表示为：

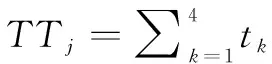
(1)

其中，tk对应航空器第k个运动状态下的滑行时间，总共包括四个运行状态；假设整条滑行路径由N个滑行路段组成，因此航空器总滑行时间的目标函数g1为各段的滑行时间之和，可以表示为：

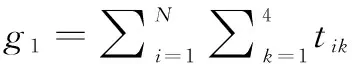
(2)

其中，tik为航空器第i个滑行路段中第k个滑行阶段的滑行时间；

根据滑行时间可以建立航空每个滑行路段的油耗模型，滑行路段j的燃油消耗量FCj的计算方式为：

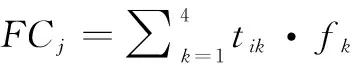
(3)

其中，fk为航空器在第k个运动状态下的油耗速率；则整条滑行速度曲线的总燃油消耗量的目标函数g2可以表示为：

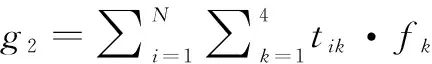
(4)

根据燃油消耗可以进一步建立航空器每个滑行路段的污染物排放模型，滑行路段j的第n种污染物排放量EIjn的确定方式为：

(5)

其中，ekn为航空器在第k个运动状态下第n种污染物的排放指数，n=1时为CO的排放指数，n=2时为HC的排放指数，n=3时为NOx的排放指数。则整条滑行速度曲线的总污染物排放量的目标函数g3n可以表示为：

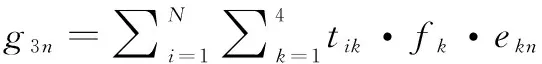
(6)

其中，当n=1时为CO的排放总量，n=2时为HC的排放总量，n=3时为NOx的排放总量。

1.3 约束条件

根据机场场面安全运行规则的相关规定，航空器在场面滑行过程中需要满足一些基本的约束条件，主要包括航空器自身的物理约束和滑行规则约束：

(1)物理约束主要包括航空器对场面滑行道和联络道的使用以及滑行避让的相关规定。如由于航空器重量和翼展的限制，不同类型航空器能通过的滑行道区域不同，航空器不能在联络道上停止等待等。

(2)滑行规则约束包括对航空器滑行速度的约束及安全间隔等，如航空器在转弯段应保持最低滑行速度vmin为10节(约5.14m/s)匀速滑行，直线滑行段的最大滑行速度vmax不能超过30节(约15.43m/s)。考虑到乘客乘坐的舒适性，航空器在滑行过程中的加速度不能太大，同时为了减少航空器的加减速时间，提升场面运行效率，参考文献[13]中的设置，将滑行过程中的加速度a固定为±0.98m/s2。

2 基于启发式搜索算法的速度曲线生成

本文提出一种启发式搜索算法，用于生成各路段的帕累托最优滑行速度曲线。通过各滑行路段的长度计算出航空器各段能达到的最大滑行速度，因此只需要针对各直线段生成其最优滑行速度曲线，最后连接组合即可得到航空器完整的滑行速度曲线。启发式搜索算法求解最优速度曲线具体步骤如下：

(1)输入分段后的滑行路径i；

(2)根据公式(1)，计算航空器能加速到最大滑行速度vmax所需要的最小理论滑行距离Dmin：

Dmin=(vs+v0)·t1/2+(vs+v4)·t4/2

(7)

其中，v0为该滑行路段的进入速度，v4为该滑行路段的脱离速度，t1表示航空器以加速度a，从进入速度v0加速到最大滑行速度vs所需要的时间，t4表示航空器以加速度a减速到脱离速度v4所需要的时间，t1和t4的计算公式如下：

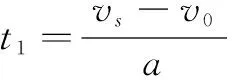
(8)

(3)遍历滑行路径中的每一个滑行路段j，若j属于转弯段，则滑行速度vturn=5.14m/s；若j属于直线段，则需要判断该段长度Dj与Dmin的关系：

① 当Dj≥Dmin时，表明该直线段的长度足够让航空器从进入速度v0加速到最大滑行速度vmax，此时生成v1从vmin到vmax步长为1m/s的速度曲线；

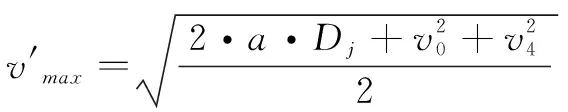
(9)

(4)根据油耗和排放模型，计算航空器每段的油耗FCj和每种污染物的排放量EIjn，根据优化目标选择每段最优的滑行速度曲线并依次连接，得到航空器完整的滑行速度曲线。

3 算例及分析

3.1 实验设置

本文实验平台为基于64位Win10操作系统下的MATLAB R2017a，实验硬件环境配置为八核Intel Core i5-8300H处理器和8GB内存。实验场景选取重庆江北国际机场，以无向图的方式建立机场场面结构数学模型，选定一架离港航空器的滑行路径进行仿真实验，如图3所示，红色路线为选取的航空器完整滑行路径，为其生成一组帕累托最优滑行速度曲线。

图3 某离港航空器滑行路径

将滑行路径按直线起始段、直线段、转弯段和直线停止段进行分段，并给定每段的进入和脱离速度，每个滑行路段的路径长度则利用Google Map手动测量获得，详细分段信息如表1所示，每一滑行段的进入速度v0也是上一滑行段的脱离速度v4。

表1 滑行路径分段信息

该离港航空器从停机位由静止开始滑行，然后以5.14m/s的脱离速度离开直线起始段，并以该脱离速度为进入速度在第二滑行直线段滑行254m，然后以5.14m/s的脱离速度脱离第二直线段，并以该速度在第三滑行转弯段匀速滑行63m，以此类推，直到航空器滑完整条滑行路径。

3.2 航空器相关参数

ICAO引擎排放数据库中提供了不同型号航空发动机在一个标准起降过程中，四个推力等级下的油耗和污染物排放指数，包括怠速阶段(7%F0)、进近阶段(30%F0)、爬升阶段(85%F0)和起飞阶段(100%F0)，其中F0为航空发动机最大额定推力。利用数据库中提供的参数，可以通过曲线拟合的方式获取航空器任意推力等级下的油耗和污染物排放指数，拟合结果如图4所示，其中油耗和NOx排放指数可以用线性函数拟合，而CO和HC排放指数则可以用指数函数拟合。

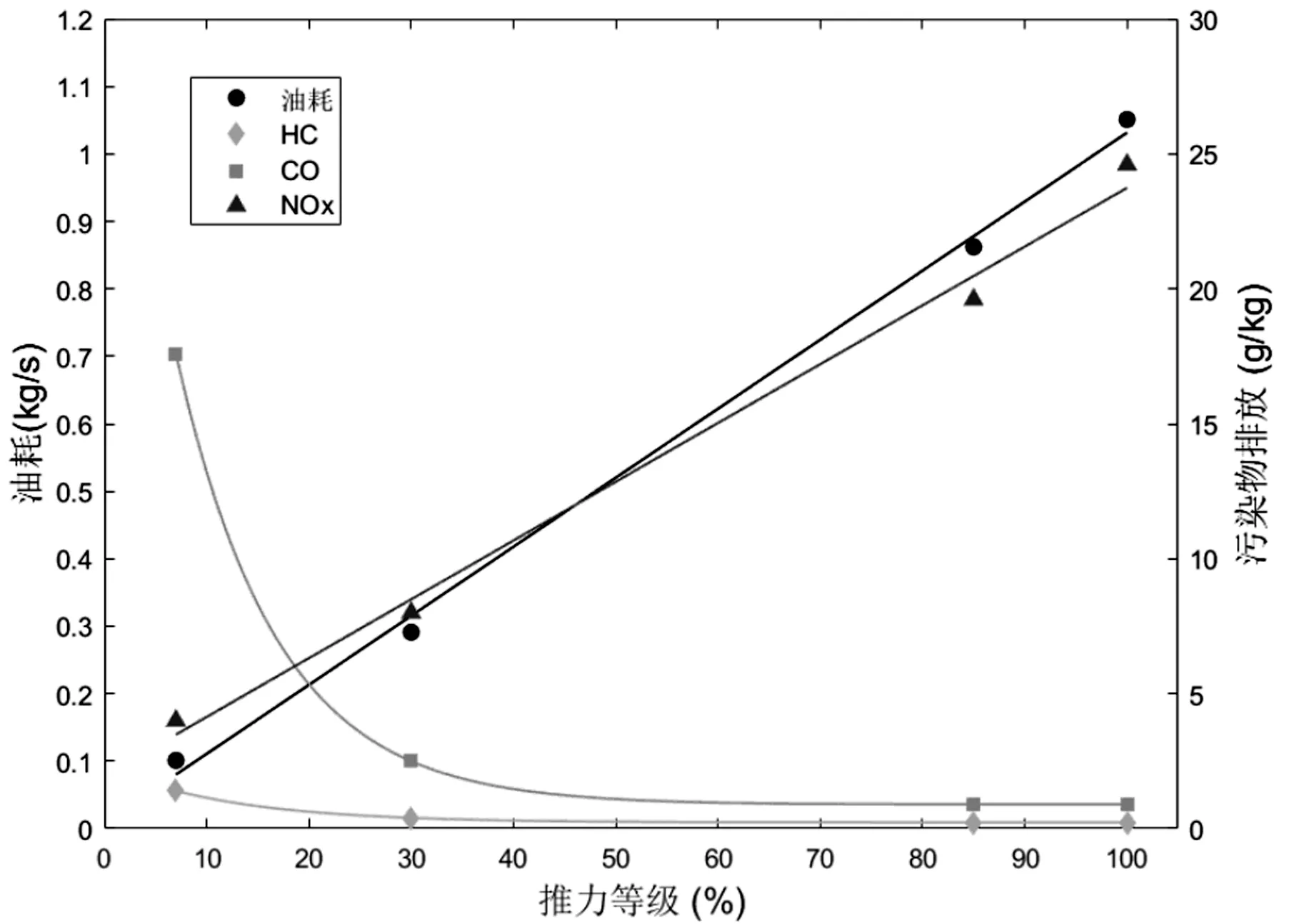
图4 油耗、排放指数在不同推力等级下的拟合曲线

本文航空器以最常见的中型客机空客A320为例分析油耗和污染物排放，其发动机识别代码为CFM56-5-A1，经过曲线拟合后，通过插值计算得出该发动机在不同滑行阶段下的油耗速率和污染物排放指数如表2所示。

表2 CFM56-5-A1发动机不同滑行状态下油耗和排放指数

3.3 实验结果及分析

表3 各直线滑行段最大滑行速度和可行解数

由于转弯路段保持最低滑行速度匀速滑行，因此只需要统计各直线滑行段的可行解数，因此根据表3可以得出整条滑行路径共有1306368种滑行速度曲线构成的可行域，根据该可行域可以得到滑行时间和油耗、滑行时间和NOx排放、油耗和CO排放以及油耗和HC排放的帕累托最优前沿，分别如图5(a)、5(b)、5(c)和5(d)所示。

(a)滑行时间-油耗帕累托最优前沿 (b)滑行时间-NOx排放帕累托最优前沿

根据图5中不同优化目标之间的帕累托最优前沿可知，航空器滑行时间和油耗并不是正相关的关系，滑行时间最短油耗和NOx排放量反而更多，这是因为在实际滑行过程中，为了达到更短的滑行时间，航空器必须频繁地进行加减速操作，导致加速持续时间长，最终导致了更多的油耗和NOx排放量；而油耗越多CO和HC排放量反而越低，这是由于油耗多意味着航空器加速持续时间长，加速阶段航空器的推力等级最高，相比匀速和减速等其他运动状态燃油燃烧更加充分，因此CO和HC排放量少，而根据ICAO排放数据库中的数据，此阶段CO和HC排放指数也为最低。

进一步选取图5中各帕累托最优前沿上左右两个端点，代表航空器滑行时间最短、油耗最低和NOx排放最低的滑行速度曲线，利用启发式搜索算法得到不同优化目标下最优的滑行速度曲线如图6(a)、6(b)和6(c)所示。

(a)滑行时间最短速度曲线

由图6可知，当以滑行时间最短为优化目标时，航空器需要通过频繁的加减速操作和更长的加速时间来达到时间最短，此时CO和HC的排放量同样最低；当以油耗最低为优化目标时，航空器减少了加减速次数和加速持续时间；当以NOx排放量最低为优化目标时，航空器在加速到最低滑行速度vmin后长时间匀速滑行，是由于匀速状态下的NOx排放指数小，在直线滑行距离较长时航空器会尽可能久的保持匀速滑行状态，不同优化目标下航空器加速次数和持续时间以及污染物排放量统计结果如表4所示。

表4 不同优化目标下加速次数和持续时间

由表4可知，当以滑行时间最短为优化目标时，航空器加速持续时间为60.41s，分别是优化目标为油耗最少和NOx排放最低时加速持续时间的2.56倍和6.53倍，这进一步说明了航空器滑行时间最短时油耗和NOx反而越高的结论。在场面交通繁忙时段，管制员可以选择滑行时间最短的速度曲线；而场面交通非繁忙时段，管制员可以选择油耗最低或排放最低的速度曲线，以灵活应对未来机场场面运行要求。

4 结语

本文针对航空器四维滑行轨迹生成中的滑行速度曲线生成问题进行了研究，综合考虑了滑行时间、油耗和三种污染物排放多个优化目标，建立了航空器各滑行路段的分段线性滑行速度曲线模型，该模型相比传统平均滑行速度或标称滑行速度能更准确的反映航空器场面滑行过程，构建了航空器滑行时间、油耗和CO、HC和NOx三种污染物排放模型，并且提出了一种启发式搜索算法生成航空器滑行速度曲线，选取重庆江北机场为实验场景，以一架中型离港航空器的滑行路径为例，分析了各优化目标之间的关系，生成了一组帕累托最优的滑行速度曲线。根据得到的帕累托最优前沿可知，航空器滑行时间最短并不意味着油耗和污染物排放最低，滑行油耗最低也不意味着污染物排放最少。在未来基于四维滑行轨迹的场面运行过程中，管制员可以根据机场要求和场面交通运行状况为航空器灵活分配不同优化目标下的滑行速度曲线。