遗传算法-模糊径向基神经网络模型预测自润滑镀层耐磨性

王亚利，于继明，王 艺

（1.济源职业技术学院，河南济源459000；2.金陵科技学院，江苏南京211169；3.中国石油化工股份有限公司西南油气分公司，四川成都610041）

自润滑镀层具有自润滑和减摩功能，可以改善金属表面的摩擦性能，因此受到广泛关注，具有良好的应用前景。目前研究和应用较多的是电镀Ni基、Ni-W基自润滑镀层及化学镀Ni-P基、Ni-W-P基自润滑镀层，无论哪种自润滑镀层，摩擦因数都是关键指标［1-6］。然而，影响自润滑镀层摩擦因数的因素较多，例如镀液温度、电镀或化学镀时间、搅拌速度、镀液pH值、电流密度、颗粒质量浓度等，且各因素之间可能存在交互作用及复杂非线性关系。

采用传统的数学方法很难表达自润滑镀层耐磨性与其影响因素之间的复杂非线性关系。近年来，神经网络以其独特的性能优势被用来建立不同类型的、可以表达某一指标与其影响因素之间复杂非线性关系的模型［7-10］。但这些模型都或多或少存在着缺陷，例如易陷入局部极小点、收敛速度慢等。笔者以化学镀Ni-P/MoS2自润滑镀层（以下简称自润滑镀层）耐磨性为研究主题，针对传统神经网络模型存在的缺陷，引入遗传算法和模糊运算建立遗传算法-模糊径向基神经网络模型（GA-FRBFNNM），旨在利用遗传算法和模糊运算的特性提升模型性能，使得模型能够更准确预测自润滑镀层耐磨性。

1 自润滑镀层耐磨性的影响因素分析

自润滑镀层耐磨性的影响因素较多，如果将所有影响因素都作为模型输入，必将导致模型极其复杂，出现收敛速度慢等问题。因此，有必要筛选出与自润滑镀层耐磨性相关性较大的影响因素。采用斯皮尔曼等级相关系数［11-12］对大部分影响因素与自润滑镀层耐磨性进行相关性分析，根据分析结果，MoS2颗粒质量浓度与自润滑镀层耐磨性相关性最大，镀液温度、化学镀时间与自润滑镀层耐磨性相关性为显著的，因此选择镀液温度、化学镀时间和MoS2颗粒质量浓度作为模型输入。

2 建立GA-FRBFNNM

2.1 训练样本和测试样本选取

镀液温度、化学镀时间和MoS2颗粒质量浓度三个因素各取四个水平，分别为镀液温度80℃、85℃、90℃、95℃，化学镀时间50 min、65 min、80 min、100 min，MoS2颗粒质量浓度1.0 g/L、2.5 g/L、4.0 g/L、5.5 g/L。各因素水平按一定规律组合进行三因素四水平的正交实验，采用HSR-2M型摩擦磨损试验仪测试所获得自润滑镀层的摩擦因数，作为衡量自润滑镀层耐磨性优劣的指标，测试条件如下：温度25℃、载荷4.9 N、摩擦行程为8 mm。测试前清除试样表面的凸起和杂物以保证平整度，每个试样都重复测3次，摩擦因数取平均值，结果如表1所示。在表1中任取10组数据作为训练样本用于模型训练，其余6组数据作为测试样本用于模型性能测试。

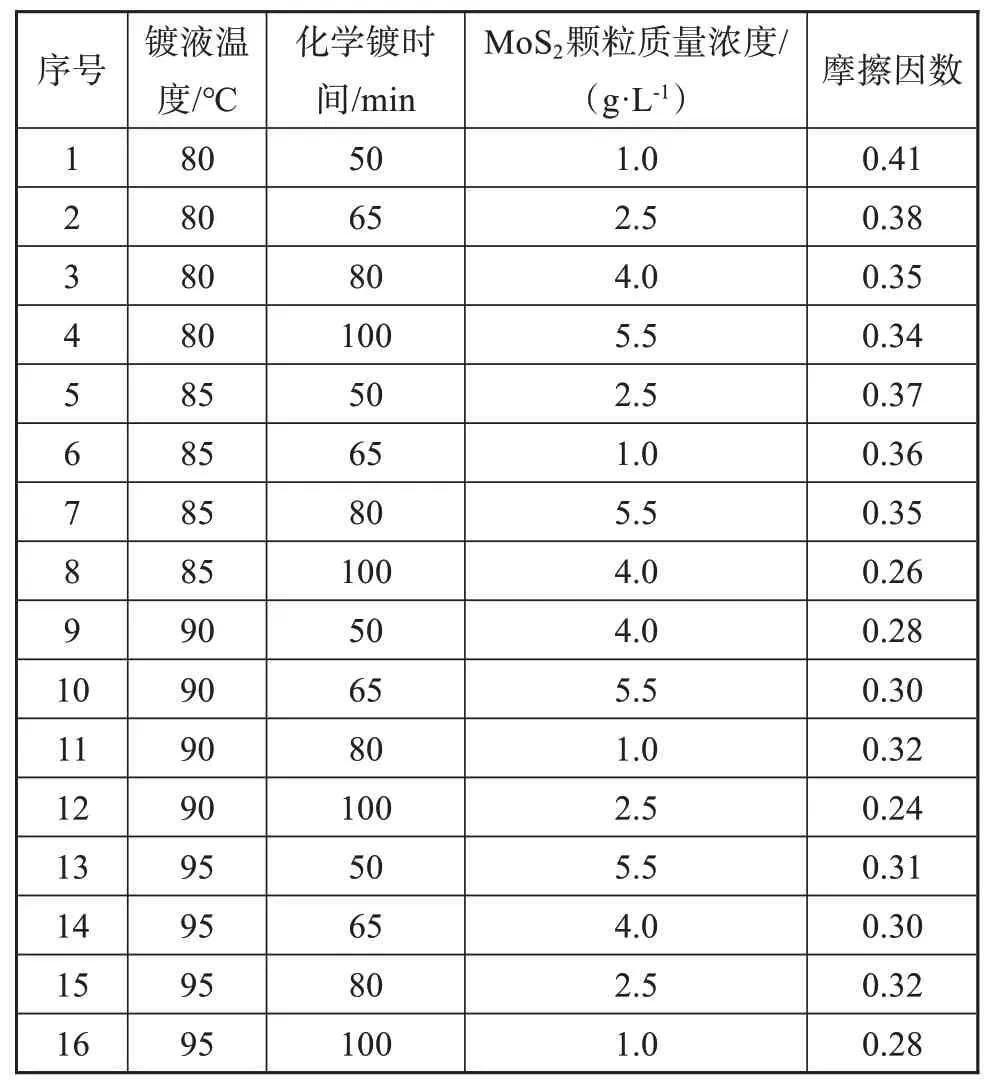
表1 正交实验结果Tab.1 Orthogonal experiment results

2.2 建立GA-FRBFNNM

模糊径向基神经网络是将模糊理论引入径向基神经网络，对径向基神经网络赋予模糊输入信号和模糊权值，使其全部节点都具有特定意义，对应模糊系统的隶属函数和推理过程。在径向基神经网络中，隐含层节点通过径向基函数队输入激励产生一个局部化相应，将隐含层的输出进行归一化，则形成网络映射如公式（1）所示：

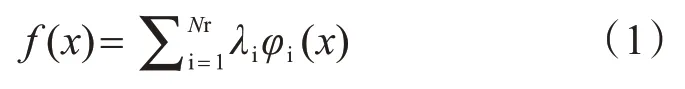
式中：f（x）表示隐含层的输出，Nr表示隐含层节点数量，λi表示输出层和隐含层第i各节点之间的链接权重，Φi（x）表示归一化的径向基函数。

可知模糊径向基神经网络各层节点之间的最优连接参数是关键，此时的模糊径向基神经网络训练采用迭代算法，存在着易陷入局部极小点等缺陷，因此引入遗传算法，搜索模糊径向基神经网络各层节点之间的最优连接参数，从而消除该缺陷。

根据神经网络理论并结合正交实验结果建立GA-FRBFNNM，其结构如图1所示。可见该模型为五层结构，其中信号传输及各层功能如下：

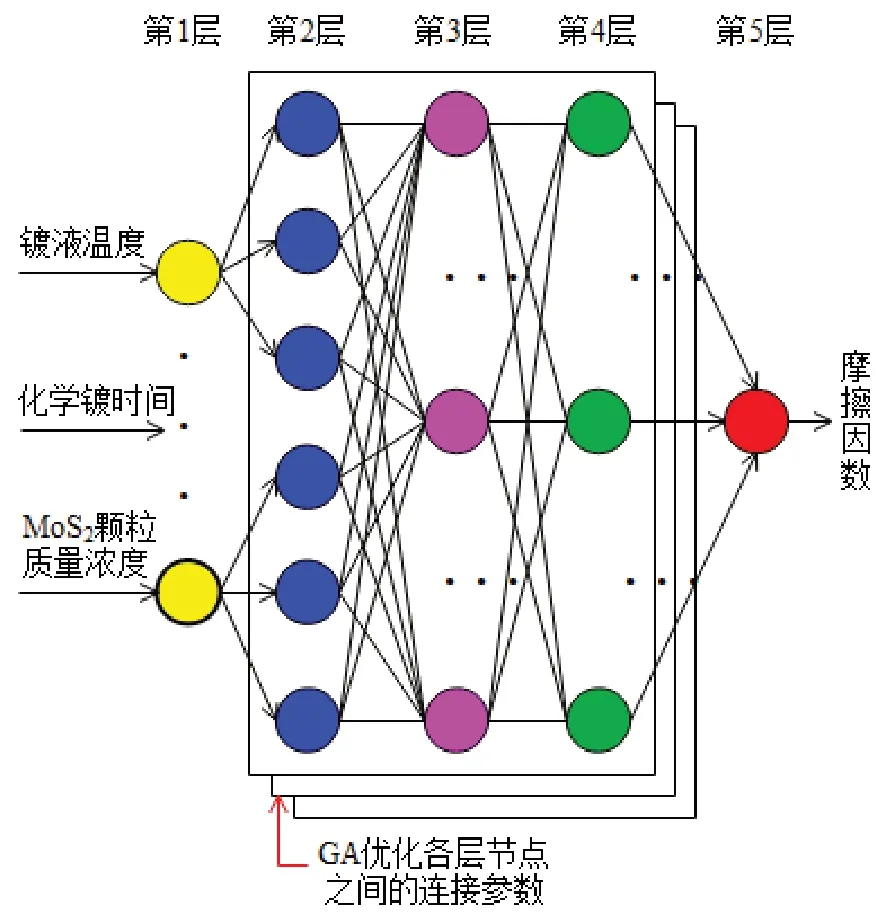
图1 GA-FRBFNNM的结构Fig.1 Structure of FRBFNNM

第1层：输入层。将镀液温度、化学镀时间、MoS2颗粒质量浓度作为模型输入直接连接并传至下一层。

第2层：模糊化层。输入层输入的数值由隶属度函数转化后，输出至下一层，模型选用高斯函数作为各节点隶属度函数。以镀液温度为例，假设镀液温度模糊子集数量为R1，采用K均值聚类算法计算镀液温度模糊子集的隶属度函数中心c1j（j=1，2，3.......R1），将镀液温度归一化处理至［0，1］区间，根据等距原则初始化各模糊子集的聚类中心c1j，并计算初始误差ε，同时计算镀液温度样本值与聚类中心c1j的距离。将样本值重新分配到与之距离最小的模糊子集中，重新计算镀液温度模糊子集的聚类中心c1j’，并与原聚类中心对比，一直重复此操作直至两者差值小于误差ε。

第3层：规则层。各节点通过模糊运算与模糊化层的连接实现模糊规则的匹配，每个结点的输出为此结点所有输入信号的乘积。

第4层：归一化层。归一化层结点总数量等于规则层，用于对模型每条规则的实用度进行归一化计算。

第5层：输出层。实现自润滑镀层耐磨性的清晰化计算（去模糊化），得到最终输出值。

利用遗传算法搜索模糊径向基神经网络各层节点之间的最优连接参数，包括模糊化层中高斯函数的均值和标准差、归一化层与输出层之间的连接权系数。

综上所述，GA-FRBFNNM预测自润滑镀层耐磨性的流程如图2所示。使用训练样本对GAFRBFNNM模型进行训练，当模型经多次训练后误差逐步缩小。达到设定范围时，模型可以映射镀液温度、化学镀时间、MoS2颗粒质量浓度与自润滑镀层耐磨性，此时镀液温度、化学镀时间和MoS2颗粒质量浓度任取某一水平输入模型，即可获得自润滑镀层的摩擦因数。

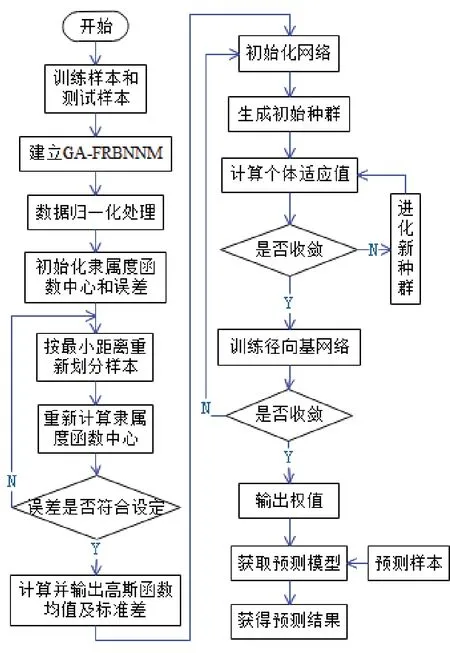
图2 GA-FRBFNNM预测自润滑镀层耐磨性的流程Fig.2 Flow for predicting the wear resistance of self-lubricating coating by GA-FRBFNNM

3 GA-FRBFNNM仿真与性能测试

3.1 GA-FRBFNNM仿真

在Matlab软件环境下进行GA-FRBFNNM仿真，模型输入是镀液温度、化学镀时间、MoS2颗粒质量浓度，输出是自润滑镀层的摩擦因数预测值。模糊径向基神经网络的第二层节点数为5，遗传算法设置种群规模为50，最大迭代次数为100。图3所示为GA-FRBFNNM输入的模糊隶属度函数，结合镀液温度、化学镀时间和MoS2颗粒质量浓度的取值范围，划分为低、中、高三个区域。

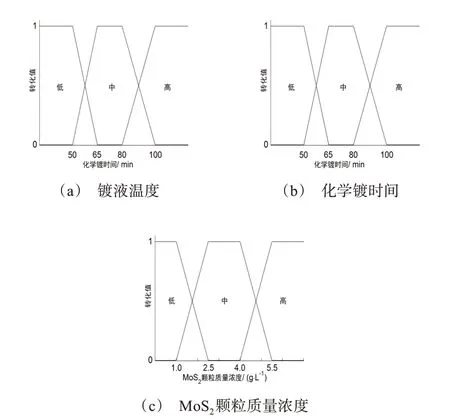
图3 GA-FRBFNNM输入的隶属度函数Fig.3 Membership function of GA-FRBFNNM input

3.2 性能测试

为了测试GA-FRBFNNM的有效性和准确性，将测试样本输入GA-FRBFNNM，然后比较输出值与真实值，同时评价预测误差是否符合要求。选用相同结构的径向基神经网络模型（RBFNNM）作为对比，将测试样本也输入RBFNNM。表2所示为RBFNNM和GA-FRBFNNM的预测值与真实值对比，可见RBFNNM和GA-FRBFNNM的预测值与真实值都存在一定的误差，原因是测试样本数据量较小，并且数据的多样性不足，从而对模型的准确性造成了一定影响。相比较而言，GA-FRBFNNM的预测值更接近于真实值。

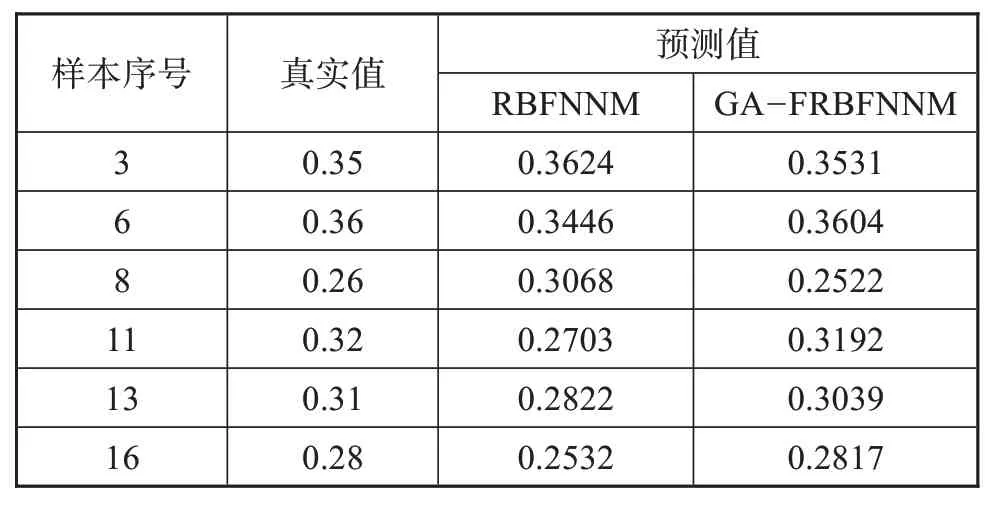
表2 RBFNNM和GA-FRBFNNM的预测值与真实值对比Tab.2 Comparison of predicted value of RBFNNM and GA-FRBFNNM and true value

图4 所示 为RBFNNM和GA-FRBFNNM的 预测误差，对于相同6组数据，RBFNNM的预测误差分 别 为0.0124、-0.0154、0.0468、-0.0497、-0.0278、-0.0268，GA-FRBFNNM的预测误差分别为0.0031、0.0004、-0.0078、-0.0008、-0.0061、0.0017。结合预测误差的分布规律可知GA-FRBFNNM的预测精度更高，预测误差在-0.01～+0.01范围内，表明该模型是有效的，可用于预测自润滑镀层耐磨性，获得较准确的预测值。为了进一步对比分析，取平均绝对百分比误差（简写为MAPE）和平均绝对误差（简写为MAE）作为指标，如表3所示。可知GA-FRBFNNM的MAPE和MAE相比于RBFNNM更低，进一步证实GA-FRBFNNM具有更高的预测精度，其性能优于RBFNNM。主要归因于引入模糊运算使得径向基神经网络全部节点都具备特定意义，另外引入遗传算法优化了训练算法，避免了模型陷入局部极小点等问题。

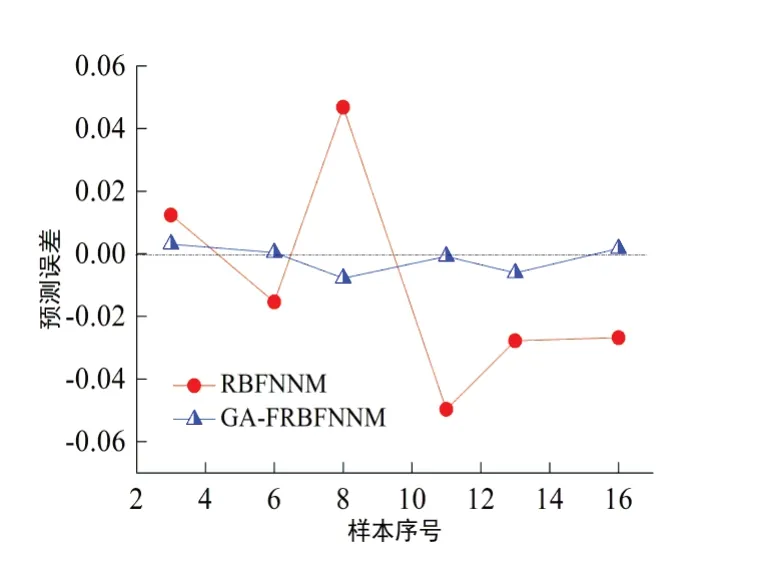
图4 RBFNNM和GA-FRBFNNM的预测误差对比Fig.4 Comparison of prediction error of RBFNNM and GA-FRBFNNM

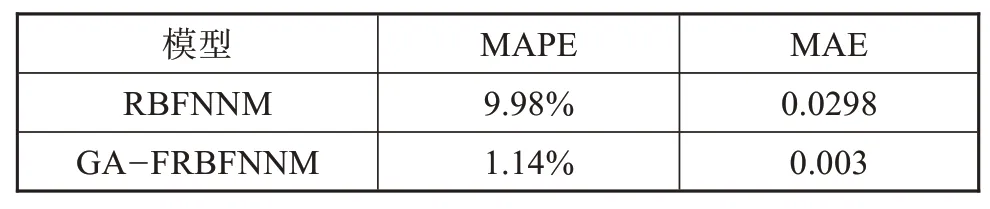
表3 RBFNNM和GA-FRBFNNM的MAPE和MAE Tab.3 MAPE and MAE of RBFNNM and GA-FRBFNNM

4 结论

（1）采用斯皮尔曼等级相关系数对大部分影响因素与自润滑镀层耐磨性进行相关性分析，确定镀液温度、化学镀时间和MoS2颗粒质量浓度作为模型输入。

（2）RBFNNM和GA-FRBFNNM的预测值与真实值都存在一定误差，相比较而言，GA-FRBFNNM的预测值更接近于真实值，具有更高的预测精度，其性能优于RBFNNM。主要归因于引入模糊运算使得径向基神经网络全部节点都具备特定意义，另外引入遗传算法优化了训练算法，避免了模型陷入局部极小点等问题。