坡地建筑结构设计的关键问题与应对方法

薛晓娟， 江 毅， 林乐斌， 易伟文

(华南理工大学建筑设计研究院有限公司， 广州 510641)

0 引言

坡地建筑依山而建，既能与自然良好结合，又可以节约用地，减少土方开挖量。尤其在山地城市，近年来随着房地产行业的蓬勃发展以及城市用地的日渐减少，坡地建筑越来越受到人们的青睐。坡地建筑结构是底部竖向构件的约束部位不在同一水平面上且不能简化为同一水平面的结构，其按接地类型可分为吊脚结构、掉层结构等形式[1]。

风荷载取值和地震作用放大、底部不等高嵌固、基础设计难度较大是坡地建筑结构设计的关键问题。本文以实际工程为依托，针对这些关键问题提出一些应对方法。

1 工程概况

六盘水市民族中学位于六盘水市教育城东南侧。建设场地为山地，地势起伏明显，山体整体落差高达132m。教学楼建筑结合地形设计了四个大平台，建筑依山而建，布置在各大平台之上，总建筑面积为2.9万m2。场地平整后，建筑场地的西南角最低，地面绝对标高为1 981.5m，建筑场地的北侧最高，地面绝对标高为2 020.1m，建筑柱底标高最大高差达38.6m，建筑场平图见图1。建筑总层数为14层，总高度为52.2m，建筑典型剖面图见图2。

图1 建筑场平图

图2 建筑典型剖面图

2 设计依据及荷载取值

本工程的结构设计使用年限为50年，因属抗震设计中的乙类建筑[2]，建筑结构安全等级为一级，结构重要性系数γ=1.1。教学楼主要使用功能为教室、办公等，根据建筑使用功能的要求，楼面活荷载按照《建筑结构荷载规范》(GB 50009—2012)[3](简称荷载规范)要求取值。

2.1 风荷载

本工程风荷载取50年一遇的基本风压0.35kN/m2，地面粗糙度类别按B类，建筑体型系数取1.3。风振系数按荷载规范要求取值。根据荷载规范第8.2.2条，对于山区的建筑物，风压高度变化系数不仅可按平坦地面的粗糙度类别确定，而且需要考虑修正系数。以本工程中最高位置的单体为例，山峰高度为132m，建筑物顶部距离建筑物地面高度z=35m，对山峰，修正系数取κ=2.2，山峰在迎风面一侧的坡度α=20°，按荷载规范公式计算，山顶处的风压高度变化系数的修正系数ηB=2.94。山脚处的风压高度变化系数的修正系数ηB=1，建筑物顶部修正系数按山顶处与山脚处线性插值确定。经过计算，风压高度变化系数放大值η取1.5。

2.2 地震作用

本工程所在地区设防烈度为6度(0.05g)，设计地震分组为第二组，场地类别为Ⅱ类，特征周期Tg=0.40s。抗震设防类别属于乙类，按上述参数进行地震作用计算，按7度采取相应的抗震措施(提高一度)。根据《建筑抗震设计规范》(GB 50011—2010)(2016年版)[4](简称抗震规范)强制性条文4.1.8条规定：当需要在条状突出的山嘴、高耸孤立的山丘、非岩石的陡坡、河岸和边坡边缘等不利地段建造丙类及丙类以上建筑时，除保证其在地震作用下的稳定性外，尚应估计不利地段对设计地震参数可能产生的放大作用，其地震影响系数最大值应乘以增大系数。根据条文说明，地震力放大系数与突出地形的高差H、突出地形的平面距离L、坡降角度的正切H/L以及场址距突出地形边缘的相对距离L1等参数有关。本工程中，H=130m，H/L=0.38，L1=0，因此地震影响系数的放大系数取1.4。

3 结构扭转位移比分析

3.1 结构初始模型

为减少结构的不规则程度，根据建筑设计平台及其平面布置，建筑结构由防震缝分为6个结构单体(图3)。各单体层数、建筑高度、柱底高差见表1。A1栋柱底最大高差最大，体量也最大，后续分析均选择A1栋做深入分析研究，A1栋初始模型见图4，5。

图3 防震缝分布图

图4 A1栋初始模型三维图

采用计算软件YJK按实际建筑柱底标高建立各单体初始模型。对初始模型进行结构整体分析，结果显示A1栋单体除扭转位移比外，其他各项整体指标均能满足抗震规范和《高层建筑混凝土结构技术规程》(JGJ 3—2010)[5]要求。各单体扭转位移比见表2，均远超规范限值1.5。

各单体初始模型信息表1

图5 A1栋初始模型西侧典型剖面图

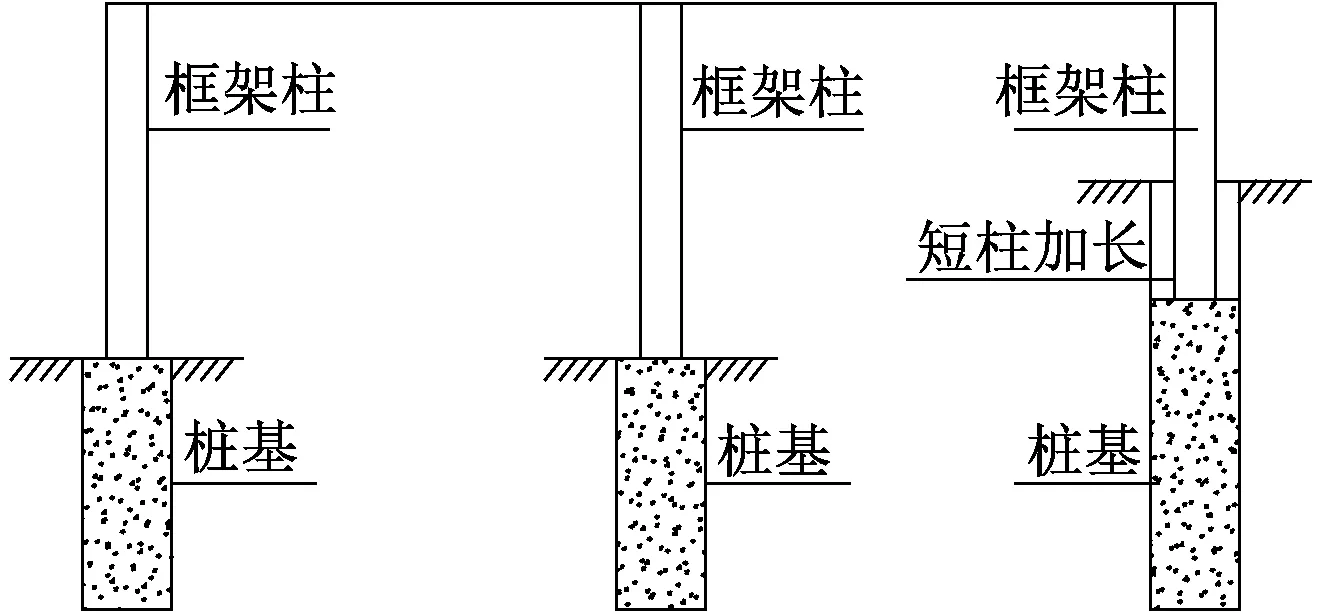
图6 加长短柱做法示意

图7 增大长柱截面刚度做法示意

图8 设置连系梁做法示意

各单体初始模型扭转位移比 表2

3.2 扭转位移比超限应对方法

由于坡地建筑结构的底部不等高嵌固，竖向构件抗侧刚度差异较大，如不采取措施，结构扭转位移比很难满足规范限值要求。而震害表明，底部不等高嵌固时，刚度较大的短柱上地震剪力比较集中，其在地震过程中更容易破坏。王丽萍[6]等对汶川地震中典型坡地建筑结构房屋进行了震害调查，发现坡地建筑结构中大量底部短柱破坏，边柱和角柱破坏更严重，这些都反映了扭转位移比超限对于结构抗震极其不利。因此结构设计中应采取特殊措施来减小扭转位移比，尽量使结构刚度均匀。

本项目根据各单体不同情况，主要采用了以下几种应对方法，将结构扭转位移比控制在规范限值1.5[5]以内。

3.2.1 加长短柱

底部柱底标高不同，柱长h差异较大，导致结构中各柱的抗侧刚度12EI/h3差异较大，结构扭转位移比易超限。短柱加长使各柱的h尽量接近，刚度趋于均匀，结构扭转位移比得到改善。加长短柱的周边用塑料泡沫块体填充，短柱加长做法示意见图6。该方法适用于底部嵌固标高差异较大且短柱较少的情况。本项目中各栋均有用到该方法。

3.2.2 增大长柱截面刚度或设置连系梁

增大长柱的截面刚度EI或在长柱区域设置连系梁均可使扭转位移比得到改善，该方法适用于长柱较少的情况。增大长柱截面刚度、设置连系梁做法示意分别见图7,8。本项目中A1栋、C1栋采取增大长柱截面刚度和设置连系梁[7]的方法。

3.2.3 设置防震缝

通过设置防震缝将长柱区域和短柱区域分为不同的结构单元，将结构扭转位移比分别统计，互不影响。此方法适用于短柱较多且短柱与长柱长度差异较大的情况。本项目中A1栋、C1栋和C2栋北侧绿化平台与主体结构之间均采用了此方法。

3.2.4 短柱设计为摇摆柱

摇摆柱上下端铰接，只承受重力荷载，不提供侧向刚度，因此对结构整体刚度分布无影响，对结构扭转位移比影响较小。该方法适用于短柱区域为单层结构、短柱较少且与长柱高度差异较大的情况。

实际工程中，一般需要根据具体情况综合采用上述几种方法才能有效减小结构扭转位移比。

4 结构模型调整前后对比分析

采用上述方法调整后，各单体模型扭转位移比见表3，与初始模型相比有了明显改善,其中A1栋调整后模型见图9，10。

调整后各单体模型扭转位移比 表3

图9 A1栋调整后模型三维图

图10 A1栋调整后西侧典型剖面图

4.1 整体指标对比

以单体A1栋为例论证调整结构扭转位移比的必要性。调整前后A1栋整体指标对比见表4。由表4可知，调整前结构在X向和Y向的结构整体刚度差异较大，调整后X向和Y向的结构整体刚度趋于均匀；X向地震作用下结构基底剪力减小约20%；由于初始模型中首层存在多个短柱，首层与上一层在X向和Y向刚度比均高达30以上，调整后楼层刚度比明显减小，趋于正常范围；而初始模型最大扭转位移比高达2.10，远超规范限值1.50，调整后模型最大扭转位移比为1.49，得到明显改善。

4.2 框架柱地震剪力对比

A1栋共计41根落地框架柱，由于柱底标高相差较大，针对结构扭转位移比严重超限问题，除了局部采用设置防震缝、增大长柱截面刚度的方法外，主要采用了加长短柱的方法。按从南到北、从西向东的顺序统计底部各柱柱长，大部分短柱加长1.5～3.5m，北侧西部柱加长4.5～5.5m，北侧东部柱加长3～8m。调整后，柱底标高相差最大为10.1m。大部分柱底标高趋于均匀，由南向北平缓过渡。调整前后各框架柱柱长对比见图11，各框架柱柱底地震剪力对比见图12。

图11 调整前后各框架柱柱长

图12 调整前后框架柱柱底地震剪力对比

调整前后A1栋主要整体指标对比 表4

从图12可见，调整前各框架柱柱底地震剪力相差较大，由于41号柱(东北角短柱)柱底标高最高，绝对标高为1 999.6m，与最低柱底标高相差18.1m，且柱长仅有0.6m，此区域结构刚度最大，因此在X向地震作用下41号柱柱底地震剪力占总地震剪力的比例最大，高达77%；而Y向地震剪力集中在6个柱子上，占总地震剪力的96%。说明原结构确实不合理，出现很多因刚度过分集中或扭转过大造成的受力异常，这也是应进行结构优化调整的原因。而按前述方法调整后的模型中，各框架柱的柱底地震剪力趋于均匀，与结构设计概念判断一致。另外，在Y向地震作用下，A1栋初始模型西南部的部分柱底地震剪力与其他柱剪力反号，这是因为西北侧接地高端的短柱刚度很大，通过刚性楼板对西南侧接地低端框架形成了一个中部水平支座，调整后此现象得以改善。

4.3 罕遇地震下的静力弹塑性对比分析

为进一步说明扭转位移比严重超限带来的问题，采用有限元分析软件Perform-3D对A1栋调整前后的模型进行罕遇地震下的静力弹塑性分析。分析基于如下假定：水平推覆荷载沿楼层分布采用小震下CQC法计算得到的水平地震力分布形式；框架梁两端设置M铰，框架柱两端设置纤维铰。

构件损伤评定标准 表6

按照抗震规范的6度罕遇地震反应谱，采用FEMA440等效线性法，将Pushover曲线中能力谱曲线与需求谱曲线的交点作为结构性能点。调整前后结构在性能点处基底剪力、最大层间位移角见表5。

结构在性能点处基底剪力与最大层间位移角 表5

从表5中可见，调整前后的模型在性能点处层间位移角均满足规范限值1/50的要求，仅从层间位移角难以评估结构及构件的具体损伤程度，也难以衡量两个模型抗震性能的优劣。因此，采用基于构件变形及材料应变层次的性能指标来评估各类构件的损伤程度。参考美国规范FEMA 356[8]，ASCE-41-13[9]及抗震规范附录M，对各类构件的轻微损伤、轻度损伤、中度损伤和严重损伤的量化评定标准见表6。以X向性能点处柱受压损伤情况为例，描述两个模型在构件损伤分布及损伤程度上的差异。图13,14分别为初始模型、调整后模型X向性能点处柱受压情况。从图13,14可看出，初始模型各柱受压损伤主要集中在短柱附近，其中41号柱损伤最为严重，达到严重损伤；调整后模型各柱受压损伤分布较为均匀且程度较轻，基本不超过中度损伤。

图13 初始模型X向性能点处柱受压情况

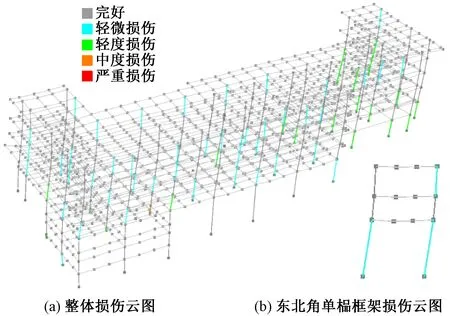
图14 调整后X向性能点处柱受压情况

两个模型在整个推覆过程中各构件损伤出现的顺序见图15。由图15可见，初始模型结构刚度较大，调整后结构刚度减小，结构整体延性得到改善。初始模型在X向推覆过程中结构的破坏机制为：首先柱钢筋受拉屈服，随后梁出现塑性铰；随着推覆的进行，出现塑性铰的梁数量不断增加，塑性转角不断增大，之后结构达到大震性能点；最后，柱混凝土被压碎。其中柱钢筋受拉屈服(41号柱)早于梁出现塑性铰，按现行规范抗震等级三级采取抗震措施仍难以保证实现“强柱弱梁”的屈服机制，而调整后模型则是梁先于柱出现塑性铰。

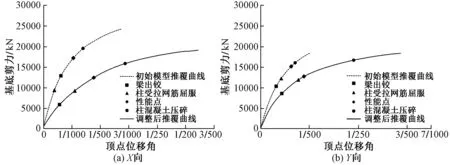
图15 主要抗侧力构件损伤状态出现顺序图

为进一步比较调整前后模型抗震性能的优劣，且考虑到实际地震震中烈度可能超出该地区的设防烈度，故将地震作用增大至7度(0.1g)、7度(0.15g)、8度(0.2g)罕遇地震，对比调整前后模型是否存在性能点。各性能点在能力曲线上位置如图16所示，各性能点对应的基底剪力、最大层间位移角见表7。

由表7和图16可见，调整前模型承载力及刚度均大于调整后模型，但延性较差，在8度(0.2g)罕遇地震下不存在性能点。而调整后模型延性较好，结构在维持稳定的前提下，变形能力较好，在8度(0.2g)罕遇地震下仍存在性能点，抗震性能优于调整前模型。

图16 不同地震烈度下调整前后模型性能点对比

综上所述，底部柱刚度差异越大，扭转位移比越大，地震剪力越容易集中在角部短柱上，短柱越容易破坏，结构整体抗震性能越差。因此，调整框架柱抗侧刚度使其趋于均匀，改善扭转位移比是必要的。

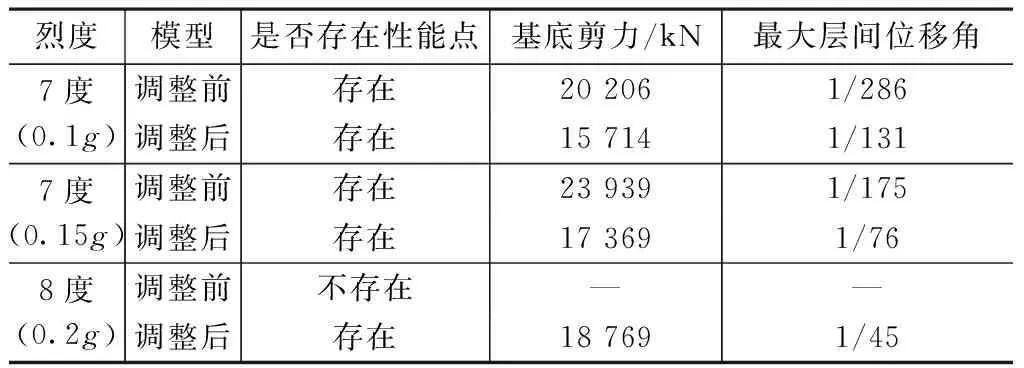
不同地震烈度下结构在性能点处整体指标 表7

5 基础设计

坡地建筑结构基础的设计重点为：1)建筑物基础对边坡整体稳定性的影响，《建筑地基基础设计规范》(GB 50007—2011)[10]在第3.0.2条中指出，建造在斜坡上或边坡附近的建筑物和构筑物，尚应验算其稳定性。同时在第5.4节中提出针对天然基础的具体控制方法。2)相邻基础间的相互影响，高处基础可能对低处基础产生附加应力。

本工程岩面高低起伏，基础形式以人工挖孔桩为主，局部采用墩基础或独立基础，桩端持力层为中风化石灰岩层(④层)，要求桩端阻力特征值不小于4 000kPa，桩径为1.2～1.8m。由于基础持力层为中风化石灰岩层(④层)，对边坡整体稳定影响较小。偏于安全考虑，设计时将高处基础基底45°影响线设置在低处基础基底以下，以避免高处基础对低处基础产生水平力。以轴为例，各柱底标高按照上述调整后确定，基础以此标高为依据，根据嵌岩深度、相邻基础影响线、以及柱底力确定基础形式、尺寸以及基底标高，如图17所示。

图17 轴地质剖面及基础布置立面图

6 结论

本文以实际项目为依托，针对坡地建筑结构的几个关键问题进行了详细的研究，并提出一些应对方法。其中，风荷载和地震作用按规范要求考虑放大系数。由于坡地建筑为不等高嵌固，其扭转位移比超限较多，为此本工程采用了加长短柱、增大长柱截面刚度、设置连系梁、设置防震缝、短柱设置为摇摆柱等方法，尽量使结构刚度均匀，扭转位移比控制在规范限值范围内。对比分析可知，调整后结构整体刚度趋于均匀，结构整体延性增强，地震响应整体减弱，各框架柱在地震作用下的柱底地震剪力趋于均匀。罕遇地震下，短柱首先发生破坏，与设计概念和实际案例现象一致，调整后结构抗震性能优良，满足抗震性能要求，因此控制结构扭转位移比是有必要的。另外，偏于安全考虑，设计基础时将高处基础基底45°影响线设置在低处基础基底以下，以避免高处基础对低处基础产生附加应力，结构整体传力路径清晰可靠。该工程于2017年11月通过验收并投入使用，工程整体性能与运行状况良好。