减少竖向荷载作用下高层扭转体型结构附加扭矩的措施研究
钱 鹏, 何冰冰, 包联进,3, 周建龙
(1 华东建筑设计研究总院, 上海 200002;2 上海超高层建筑设计工程技术研究中心, 上海 200002;3 同济大学土木工程学院, 上海 200092)
0 引言
随着经济的迅速发展和科学技术的进步,高层建筑也呈现出飞速发展的现象。扭转体型高层建筑作为高层建筑的分支,其楼层平面循环有序地旋转,使建筑的外部轮廓更加丰富,因此得到越来越多建筑师的青睐。近年来涌现出许多扭转体型高层建筑,如迪拜卡延塔、广州塔[1]、莫斯科进化大厦[2]、深圳世茂金融中心[3]、迈阿密Grove at Grand Bay[4]、巴拿马旋转大厦、芝加哥螺旋塔、瑞典马尔默旋转大厦和上海中心大厦等[5-6]。
建筑体型的扭转通常会使结构整体受力和构件受力状态发生新的变化,特别是像外框扭转框架-核心筒高层结构(简称扭转体型结构),由于外框的扭转,在竖向荷载作用下会对核心筒产生附加扭矩,这大大增加了结构设计的难度和结构的造价,使核心筒墙肢的设计更加复杂。迈阿密Grove at Grand Bay建筑总高度约74m,总扭转角为38°,为了抵抗附加扭矩,核心筒若采用混凝土剪力墙则墙厚高达1 800mm,为了减小墙厚,最终采用800mm厚的钢板混凝土剪力墙(钢板厚100mm)[4]。因此,此类扭转体型结构在竖向荷载作用下产生附加扭转的力学原理,以及采取何种措施来有效地减小剪力墙墙厚,成为此类结构研究和设计迫切需要解决的问题。
本文以扭转体型结构作为研究对象,采用结构分析软件ETABS[7]建立了不同的结构模型,剖析竖向荷载作用下扭转体型结构产生附加扭矩的力学原理,并以此为基础提出了4种可以减小核心筒附加扭转的措施,通过理论和数值分析的方法,研究了这4种措施对减小附加扭矩的效果和一般规律。最后,根据研究结果提出减小附加扭矩的最为有效措施,为扭转体型结构设计提出切实可行的设计对策。
1 竖向荷载作用下扭转体型结构的受力特点
1.1 研究对象及分析模型
本文采用ETABS软件建立基准模型,如图1所示。基准模型采用框架-核心筒结构体系,内筒为混凝土核心筒,外框柱采用钢管混凝土柱,混凝土强度等级均为C60,钢材材质均为Q345B。基准模型共60层,每层扭转角为0.5°,结构总高度为270m,楼层平面尺寸为54m×54m,核心筒平面尺寸为27m×27m,外框柱柱距为13.5m,结构主要构件的截面尺寸详见表1。
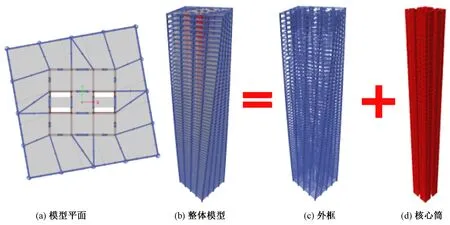
图1 基准模型平面图及三维图

结构主要构件截面/mm 表1
1.2 附加扭矩计算结果
竖向荷载作用下,扭转体型结构的核心筒和外框需承担附加扭矩,并且两者的附加扭矩大小相等、方向相反,如图2所示。
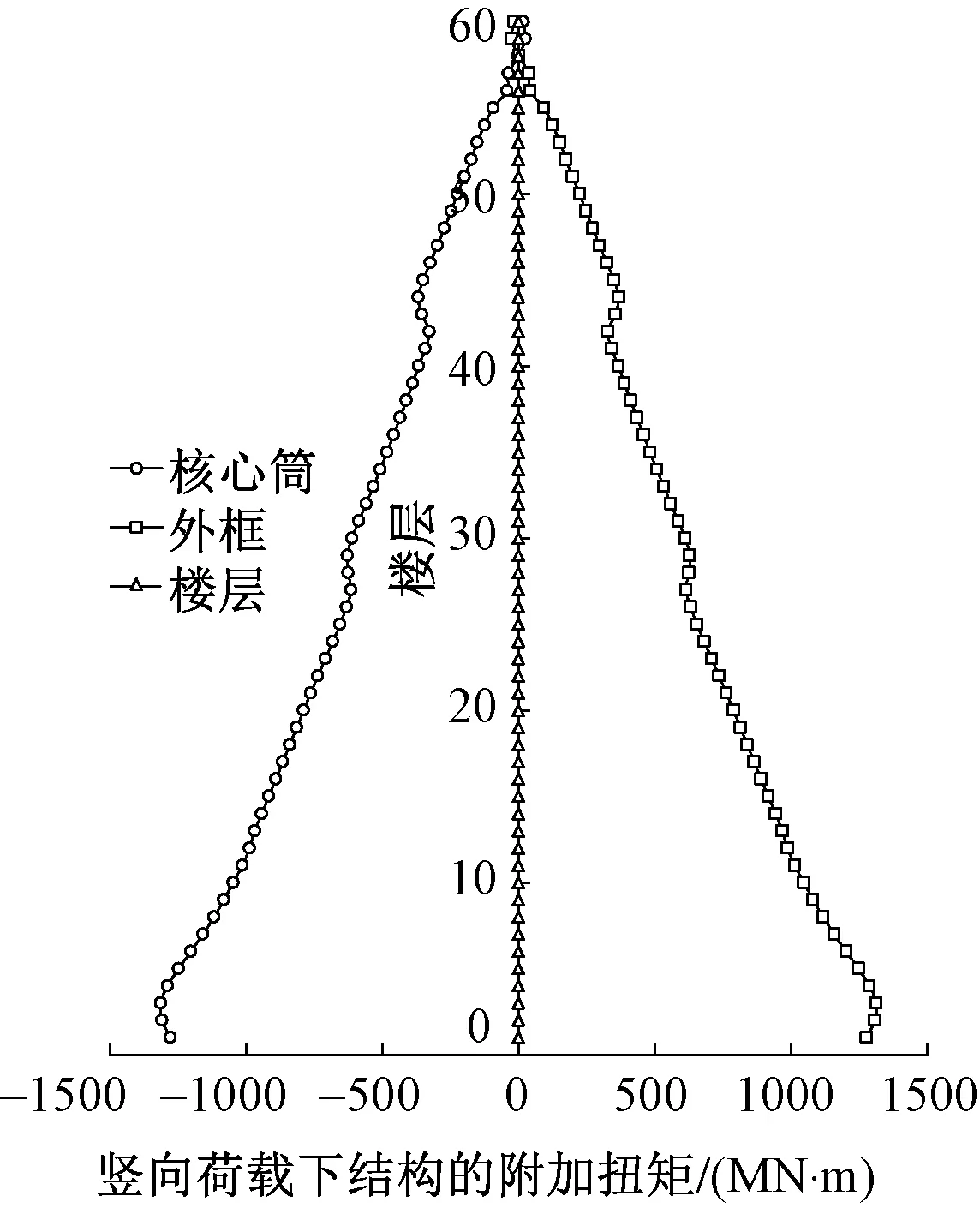
图2 竖向荷载下扭转体型结构 附加扭矩分布
1.3 附加扭转产生机理及影响因素
扭转体型结构中核心筒和外框的附加扭矩是一对互相平衡的内力,其产生的根本原因是外框斜柱的扭转变形受到核心筒的约束。如图3所示,竖向荷载作用下,楼面竖向力G可分解为沿斜柱的轴向力N和沿楼面边线的水平分力V,同一楼层面上的水平分力合成为一个作用于外框的扭矩T。当外框的抗扭刚度较弱时,该扭矩会使外框产生较大的扭转变形,而核心筒的抗扭刚度较大,将通过楼板约束外框的扭转变形,同时外框的扭矩也通过楼板传递给核心筒。外框的抗扭刚度越强,外框的扭转变形越小,核心筒对外框的约束效应也越弱,其承担的扭矩也越小。
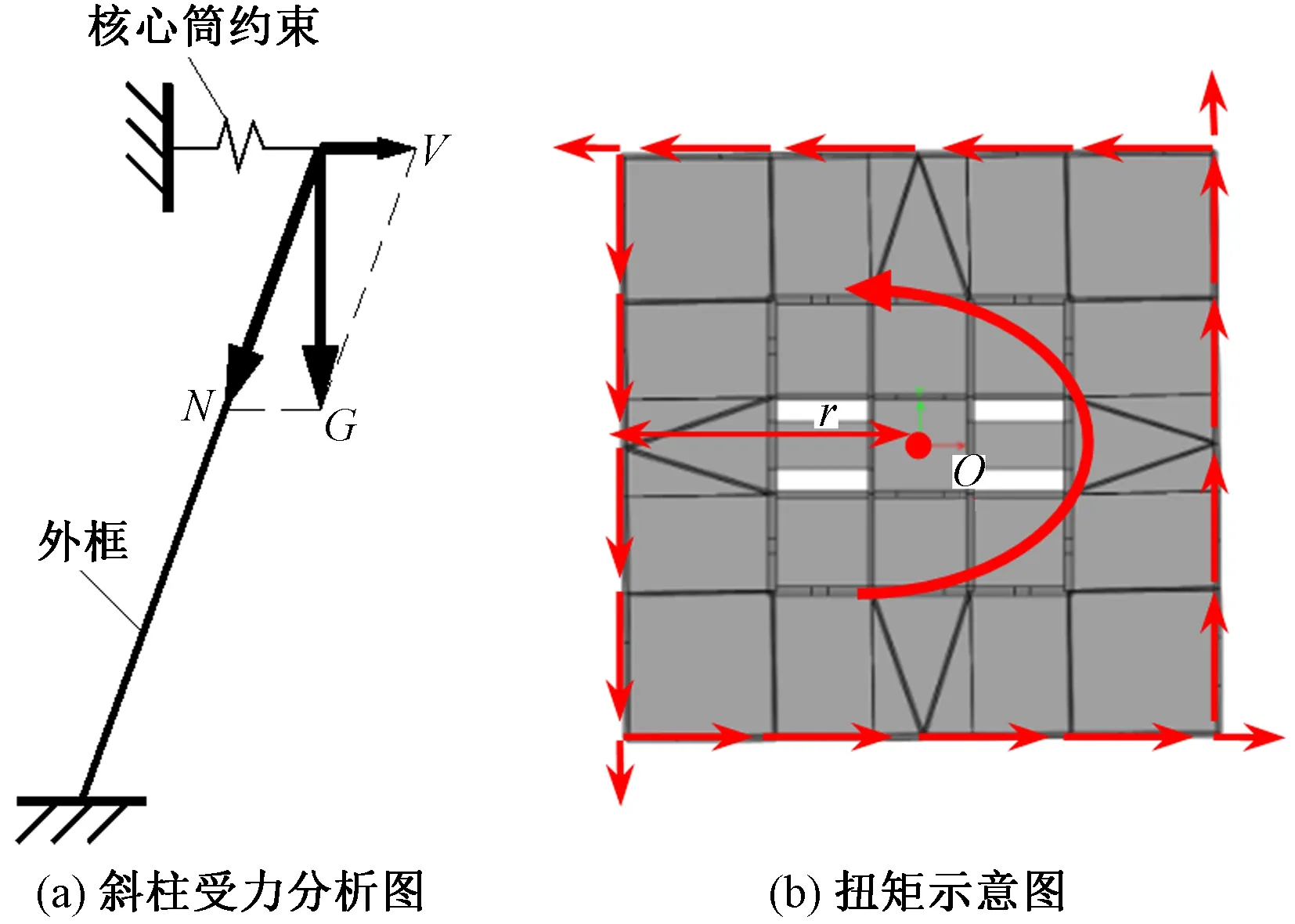
图3 附加扭矩形成示意图
为了方便对比核心筒与外框的抗扭刚度对附加扭矩的影响,将基准模型中各层的构件改为相同的截面,并调整核心筒墙厚,以改变核心筒与外框(简称内外筒)的抗扭刚度比,核心筒墙厚对附加扭矩的影响如图4所示。由图4可知,结构附加扭矩随核心筒墙厚的增大而增大,当核心筒墙厚大于300mm,即核心筒刚度达到一定值后,结构的附加扭矩基本保持不变。
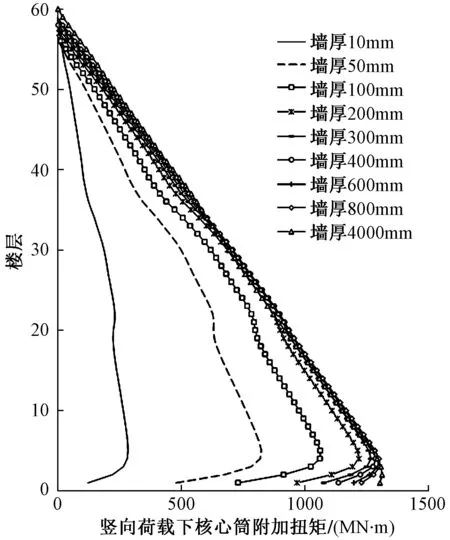
图4 核心筒墙厚对附加扭矩的影响
图5给出了附加扭矩-内外筒抗扭刚度比曲线,由图可知,附加扭矩随内外筒抗扭刚度比的增大呈非线性增长趋势,当内外筒抗扭刚度比超过50,核心筒的附加扭矩基本保持不变。常规的框架-核心筒结构的内外筒抗扭刚度比均大于50,所以可以近似将核心筒当作固定支座。

图5 内外筒抗扭刚度的影响曲线
对图6所示的某根斜柱进行分析,当结构楼层旋转θ时,外框柱倾斜角为α,α可根据式(1)确定。其中O为楼层刚心(剪心)。
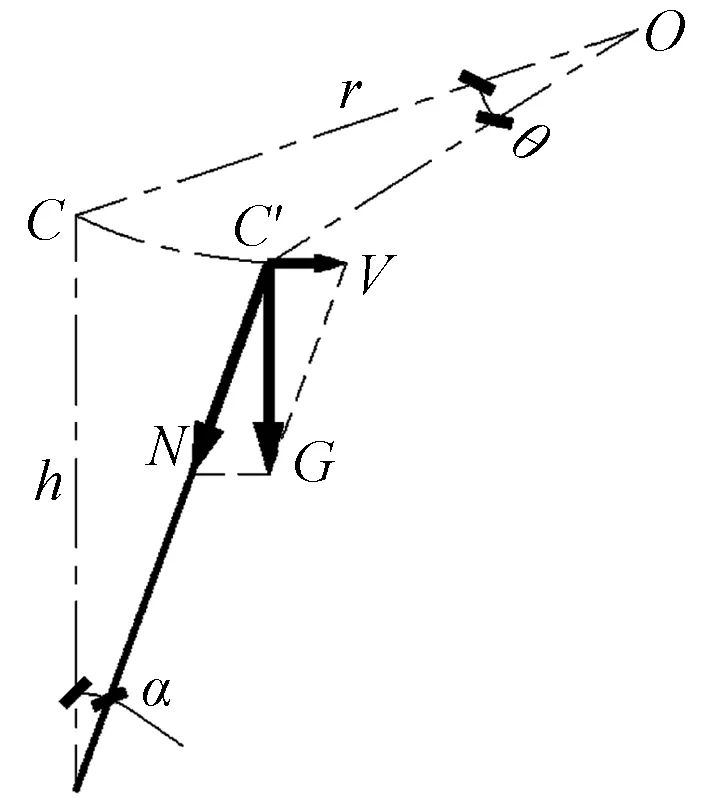
图6 斜柱受力简图
(1)
式中:θ为楼层转角;r为旋转半径;h为层高。
考虑核心筒的约束作用后,水平力在楼层平面内形成的扭矩T可按式(2)确定。
T=ηVr=ηGrtanα=ηGθr2/h
(2)
式中:α为柱倾斜角;G为竖向荷载;η为考虑核心筒约束刚度与外框刚度的水平力折减系数,η=f(kF,kC),η随kF的增大、kC的减小而减小,kF,kC分别为外框和核心筒的抗扭刚度。
由式(2)可知,核心筒附加扭矩主要与G,θ,r,h,kC和kF相关,且附加扭矩随θ,r,kC和G的减小而减小,随h和kF的增大而减小。
对于层高h、质量和结构布置沿高度均匀分布的扭转体型结构,每层竖向荷载引起的附加扭矩基本一致,将式(2)与图5中拟合曲线的表达式相结合,可以得到核心筒附加扭矩的计算公式,见式(3)。
(3)
式中:Gi为第i层传给外框的竖向荷载;Tk为第k层核心筒的累计附加扭矩;K为内外筒抗扭刚度比;θi为第i层的楼层转角;ri为第i层的旋转半径;hi为第i层的层高;ηi为第i层的考虑核心筒约束刚度与外框刚度的水平力折减系数;N为楼层总数。
将由式(3)计算得到的附加扭矩的理论值与ETABS模型得到的计算值进行对比,如图7所示。由图7可知:1)附加扭矩公式的理论值与ETABS模型得到的计算值较为接近,表明本文提出的附加扭矩计算公式具有较高的准确度。2)底部4层的ETABS模型得到的附加扭矩计算值较小,这是因为外框和核心筒的抗扭刚度随结构高度的变化趋势不同。在结构底部,核心筒的抗扭刚度主要由剪力墙的剪切刚度贡献(与GA/h相关),外筒的抗扭刚度由框架的弯曲刚度贡献(与EI/h3相关),随着层高h的减小,外框的抗扭刚度的增大幅度更大,使内外筒抗扭刚度比减小,核心筒附加扭矩随之减小。3)中间楼层有差异,是因为附加扭矩计算公式假定内外筒抗扭刚度沿结构高度为定值,而ETABS模型中的构件截面沿结构高度方向发生了变化。
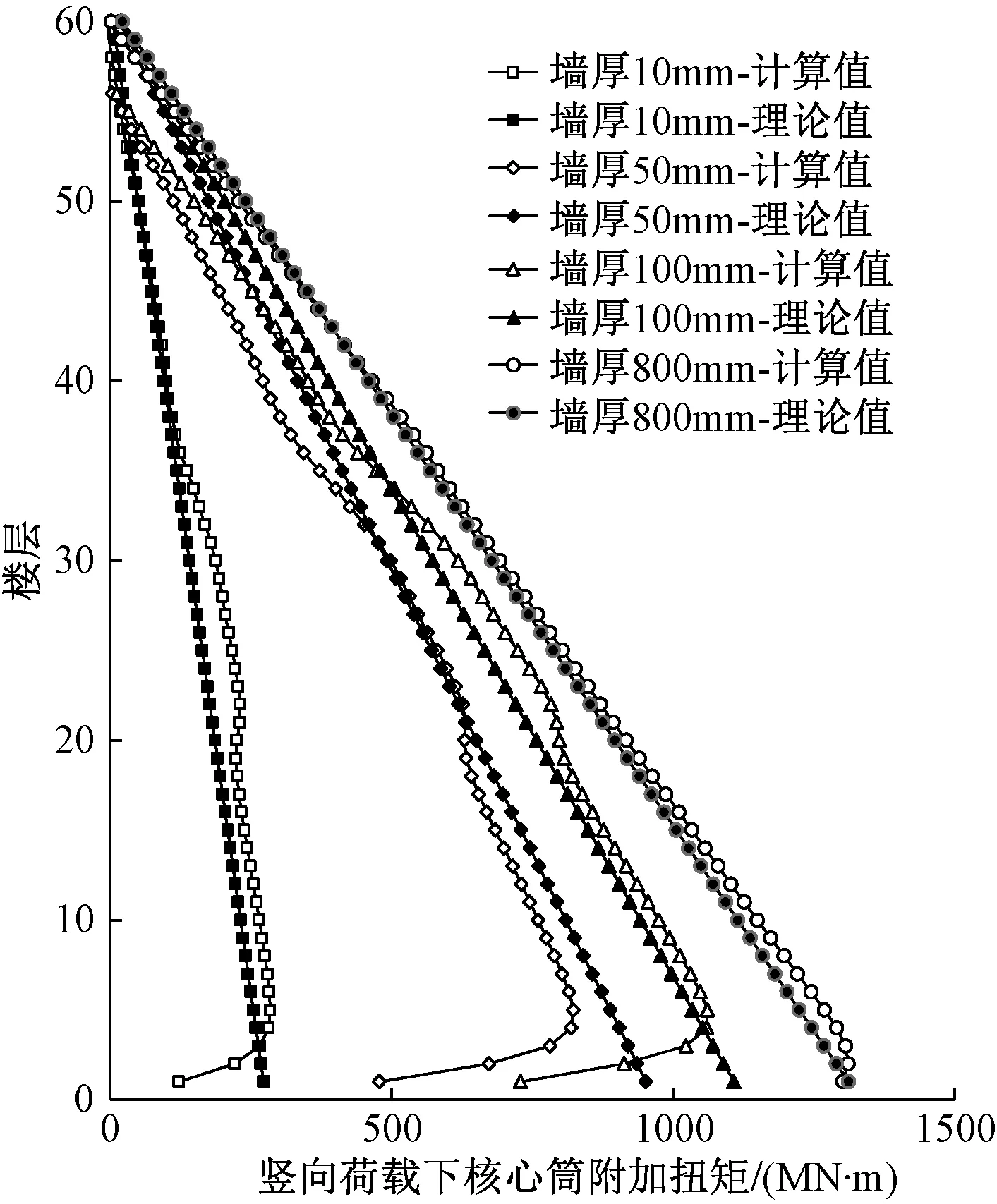
图7 附加扭矩的理论值与计算值的对比
2 减少附加扭矩的措施研究
由式(3)可知,通过减小θ,r,kC,G或增大h和kF,可以减小核心筒的附加扭矩,其中θ和h一般由建筑外型或功能确定,r和G可通过调整楼盖的布置改变结构的传力路径来实现,kF可增加结构外框的抗侧刚度来改变。
结合超高层结构常用的技术措施[8],以及已有的研究结果[9],可能减小附加扭矩的措施有:1)增加反向斜撑;2)增加中柱;3)增加环形桁架;4)增加伸臂桁架。
2.1 增加反向斜撑
分别在外框上分别增加1道、2道和4道与结构扭转方向相反的斜向支撑构件(简称反向斜撑),如图8所示,反向斜撑与钢梁的夹角为45°,其截面刚度应与斜柱相协调,模型中反向斜撑截面均为□1 200×600×40×40。
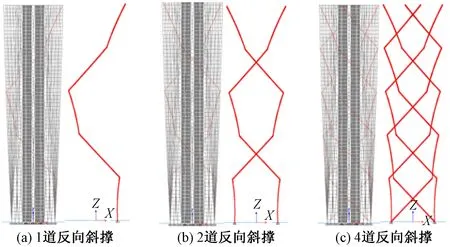
图8 反向斜撑布置图
增加反向斜撑前后,竖向荷载下核心筒的附加扭矩如图9所示。由图9可知:1)增加反向斜撑后,核心筒的附加扭矩明显减小;2)反向斜撑数量越多,核心筒附加扭矩的减小量越多,增加1道、2道和4道反向斜撑后,核心筒附加扭矩分别降低了14%,27%和45%;3)增加反向斜撑后,不同楼层核心筒附加扭矩的削减效果不同,反向斜撑与角柱连接的楼层(12,24,36,48,60层)核心筒附加扭矩的减小量较小。
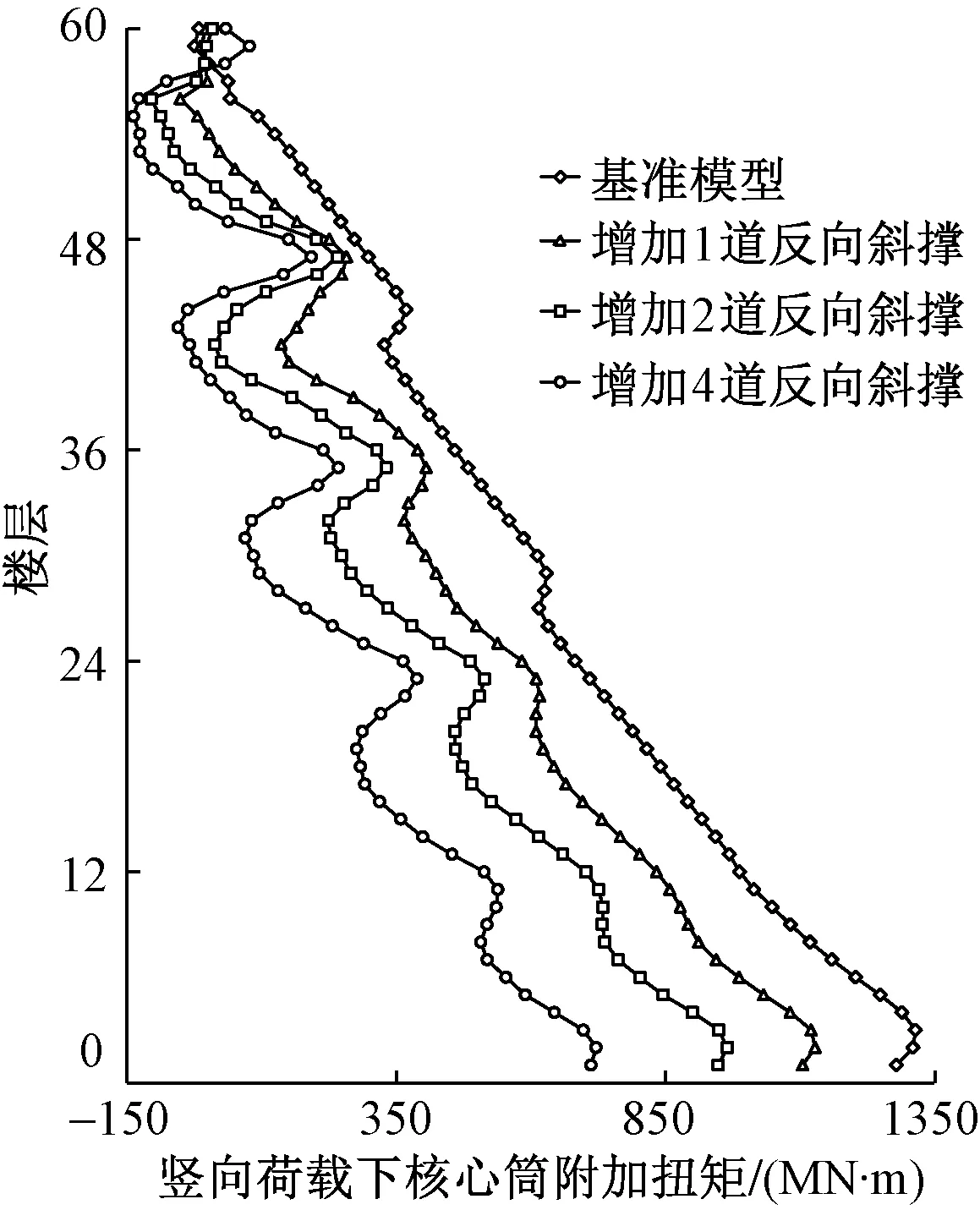
图9 反向斜撑对核心筒附加扭矩的影响
对于扭转体型结构,产生附加扭矩的主要原因是斜柱柱顶的水平位移。为了减小体型扭转对结构的不利影响,在外框中增加反向斜撑是十分有效的措施。一方面,反向斜撑承担了部分水平分力,减小了扭矩;另一方面,增加了反向斜撑的外框形成斜交网格,极大地提高了抗扭刚度,减小了外框的扭转变形,从而减小了扭转效应。理论上,当反向斜撑的截面刚度满足一定条件时,结构的扭转效应将完全消失。
如图10所示,将扭转结构某层的斜柱与斜撑取出,假定杆件端部均为铰接,图中α和β分别为斜柱、斜撑与竖直线的夹角,h为楼层层高。当斜撑使斜柱顶点在竖向荷载下的水平位移为0时,竖向荷载的水平分力全部由斜撑承担,扭转效应消失。
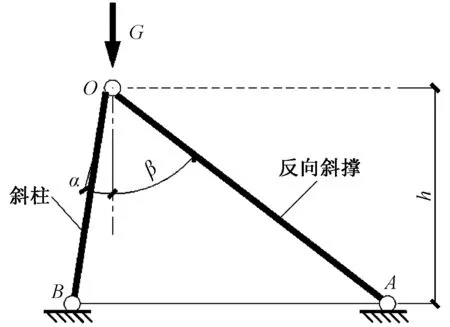
图10 斜柱-反向斜撑简化力学模型
采用图乘法计算竖向荷载G作用下柱顶O点的水平位移,如式(4)所示。竖向荷载G作用下,斜柱与斜撑的轴力图如图11所示,斜柱与斜撑的轴力
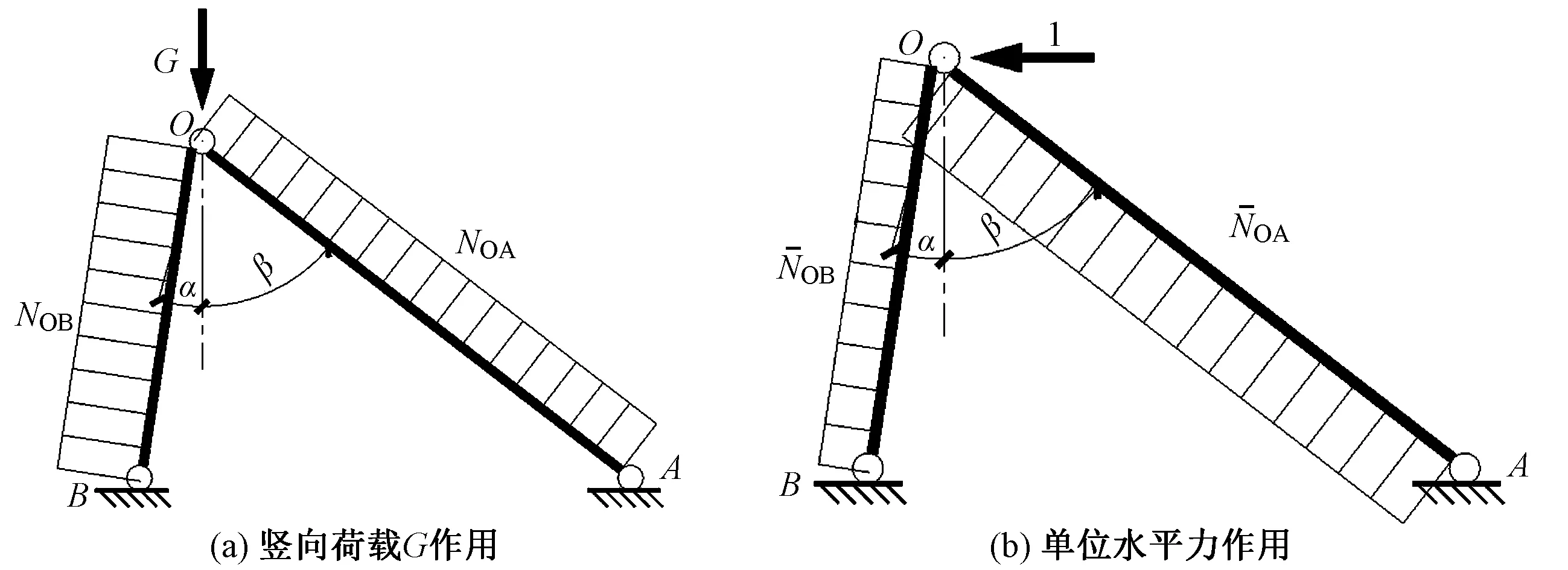
图11 斜柱与反向斜撑的轴力图
值见式(5)。
(4)
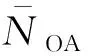
(5)
令Δ0H=0,可得到消除结构扭转效应所需的斜撑截面刚度,斜柱与斜撑的轴向刚度比(简称刚度比)见式(6)。
(6)
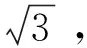

图12 约束条件的影响
由图12可知,当斜柱与斜撑两端铰接时,O点仅存在竖向位移,水平位移几乎为0,验证了式(6)的准确性;当斜柱与斜撑两端刚接时,O点的水平位移也仅为竖向位移的1.4%,表明端部约束条件对斜柱、斜撑的位移影响较小,也验证了简化模型的合理性。
将本节模型中的反向斜撑截面按照式(6)的计算结果进行调整,不同斜柱扭转方向示意图见图13。由图13可知,斜撑在外框中的位置不同,扭转半径不同,扭转变形与斜撑的夹角也不同,因此所需的斜撑刚度也不同。图中的A处柱、B处柱需要的刚度比分别为0.147和0.294,为了计算方便,全楼的刚度比取A处柱、B处柱的均值,即0.220 5。
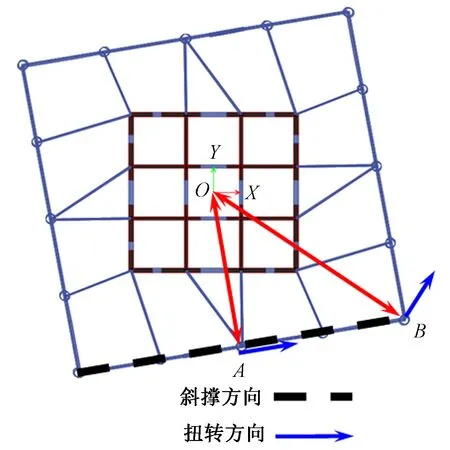
图13 不同斜柱的扭转方向示意图
当全楼刚度比分别为0.125,0.220和0.375,计算得到的核心筒附加扭矩如图14所示。由图14可知,当斜撑轴向刚度较小时,核心筒仍有较大的附加扭矩,因为斜撑不足以抵抗斜柱的水平变形;当斜撑轴向刚度较大时,核心筒也有较大的附加扭矩(扭矩符号相反),因为此时斜撑的水平分力超过斜柱,使斜柱朝反方向变形;当斜撑轴向刚度适中,核心筒附加扭矩较小。
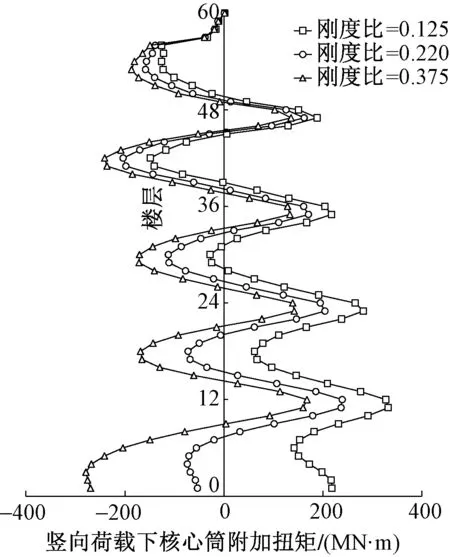
图14 刚度比对核心筒附加扭矩的影响
2.2 增加中柱
在外框柱和核心筒之间增加中柱,其截面与外框柱相同,增加中柱后的结构平面布置示意如图15所示。

图15 中柱布置示意图
增加中柱后核心筒的附加扭矩分布如图16所示。由图16可知:1)增加中柱后,恒载作用下核心筒的附加扭矩变化很小;2)增加中柱后,活载作用下核心筒的附加扭矩最大值减小了约8%。
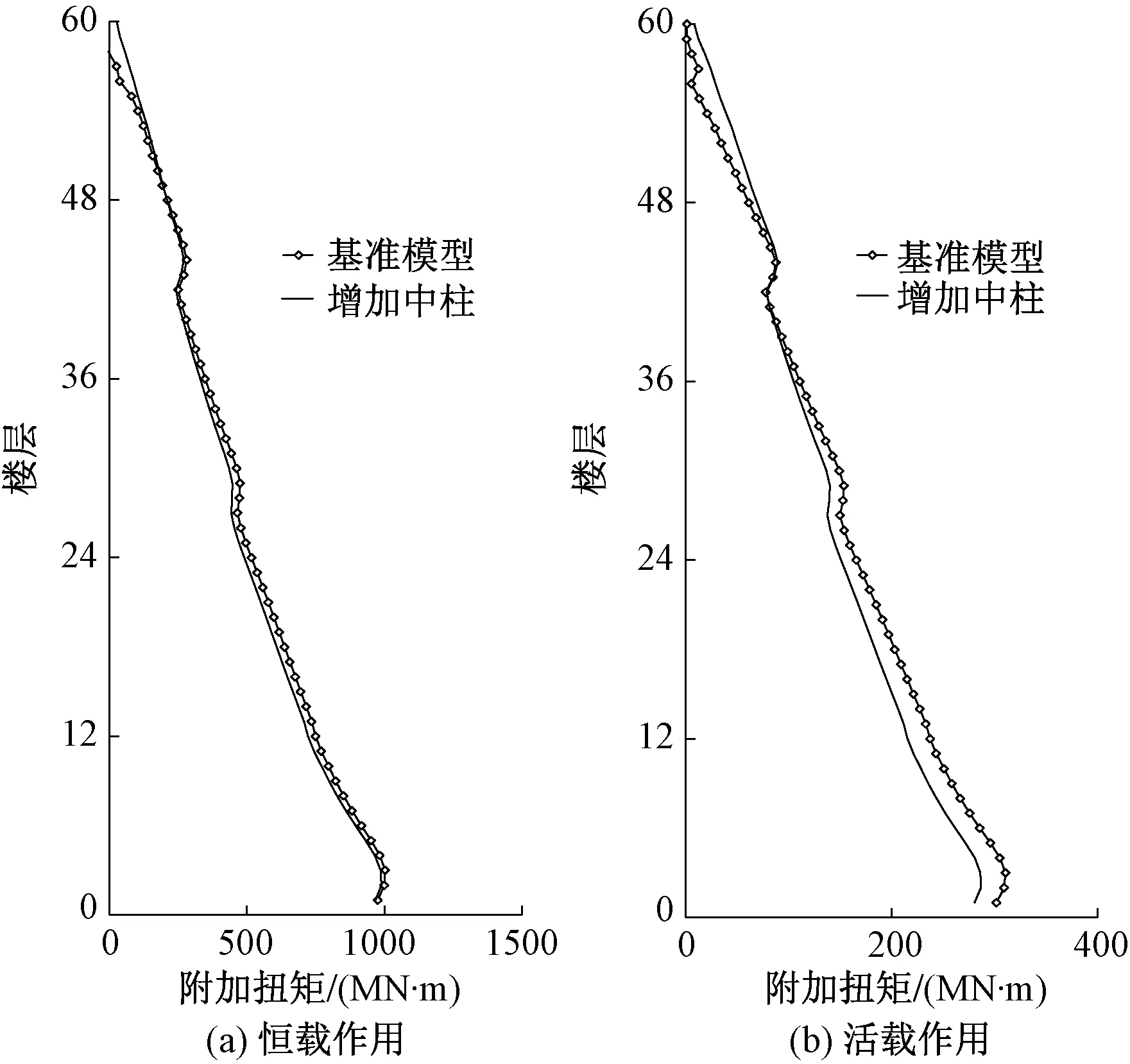
图16 中柱对核心筒附加扭矩的影响
由式(3)可知,扭矩的大小与扭转半径、竖向荷载相关。在核心筒与外框柱之间增加中柱后,大部分竖向荷载传递给扭转半径较小的中柱,从而减小了结构扭矩。
如图17所示,在扭转半径的中点增加中柱。假设核心筒以外楼面的竖向荷载为G,且中柱、边柱与核心筒的竖向刚度一致,则竖向荷载中0.5G传递给中柱,0.25G传递给边柱,根据式(2)求得核心筒的初始附加扭矩T1和增加中柱后的附加扭矩T2,见式(7)~(8)。理论上,在OC中点增加中柱后,结构扭矩最多可以降低约25%。
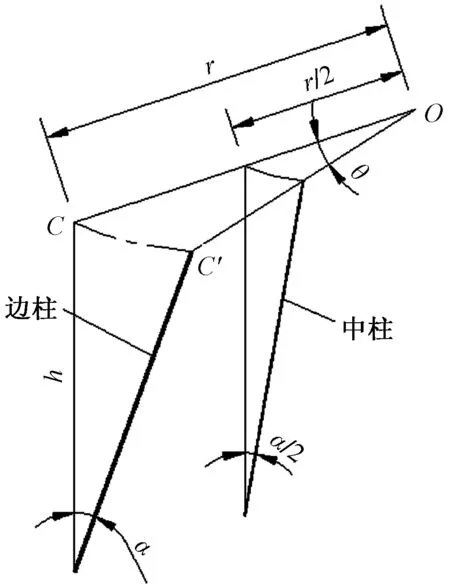
图17 增加中柱后的计算简图
(7)
(8)
式(7)和式(8)的分析均基于两个假定:1)OC中点有空间立中柱;2)竖向荷载完全按照负荷范围分配。
对于第一条假定,高层建筑的内部一般设置了核心筒,且核心筒的尺寸为建筑平面尺寸的一半,因此中柱与结构扭心的距离为0.75r,将中柱的位置代入式(7)重新计算,得到T2/T1=1.06,即增加中柱后核心筒的附加扭矩反而增加了6%。
对于第二条假定,高层建筑的外框柱截面尺寸较大,而中柱尺寸受建筑使用空间的限值,二者的刚度不同;同时外框柱与中柱的约束条件也不一致,其轴力的分配不一定与负荷面积成正比。
因此,增加中柱对核心筒附加扭矩的影响较小,甚至可能增大附加扭矩。
2.3 增加环形桁架
在结构30层和60层增加环形桁架,桁架腹杆截面为H800×400×20×30,环形桁架的布置示意如图18所示。

图18 环形桁架布置示意图
增加环形桁架前后,竖向荷载作用下核心筒的附加扭矩如图19所示。由图19可知,增加环形桁架后,桁架所在楼层以及相邻上下2~3层的核心筒附加扭矩削减效果很明显,其余楼层核心筒的附加扭矩基本不变。

图19 环形桁架对核心筒附加扭矩的影响
由1.3节的分析可知,外框与核心筒之间的层间扭转变形差值是引起核心筒附加扭矩的主要因素,环形桁架对核心筒附加扭矩的影响可通过图20说明。
图20(a)和20(b)的前3张图含义分别为:1)扭转变形。垂直于扭转半径的水平位移,u=rφ,r,φ分别为扭转半径和扭转角。2)扭转变形差值。同一楼层处,外框与核心筒扭转变形的差值Δi=uF,i-uW,i,uF,i,uW,i分别为第i层外框和核心筒的扭转变形。3)层间扭转变形差值。相邻楼层的扭转变形差值的变化量,即Δi-Δi-1。
如图20(a)所示,对于外框、核心筒抗扭刚度沿竖向均匀分布的结构,外框与核心筒受到的扭矩大小相等,其扭转变形沿高度方向均匀增大,各楼层的扭转变形差值增量基本相等,核心筒在各楼层受到的附加扭矩也基本相同,因此核心筒累计附加扭矩从上到下逐渐增大。
如图20(b)所示,设置环形桁架后,外框的抗扭刚度发生突变而核心筒的抗扭刚度不变,环形桁架楼层处扭转变形差值的增量为负值,因此该楼层的附加扭矩与其他楼层相反,该层核心筒累计附加扭矩减小。
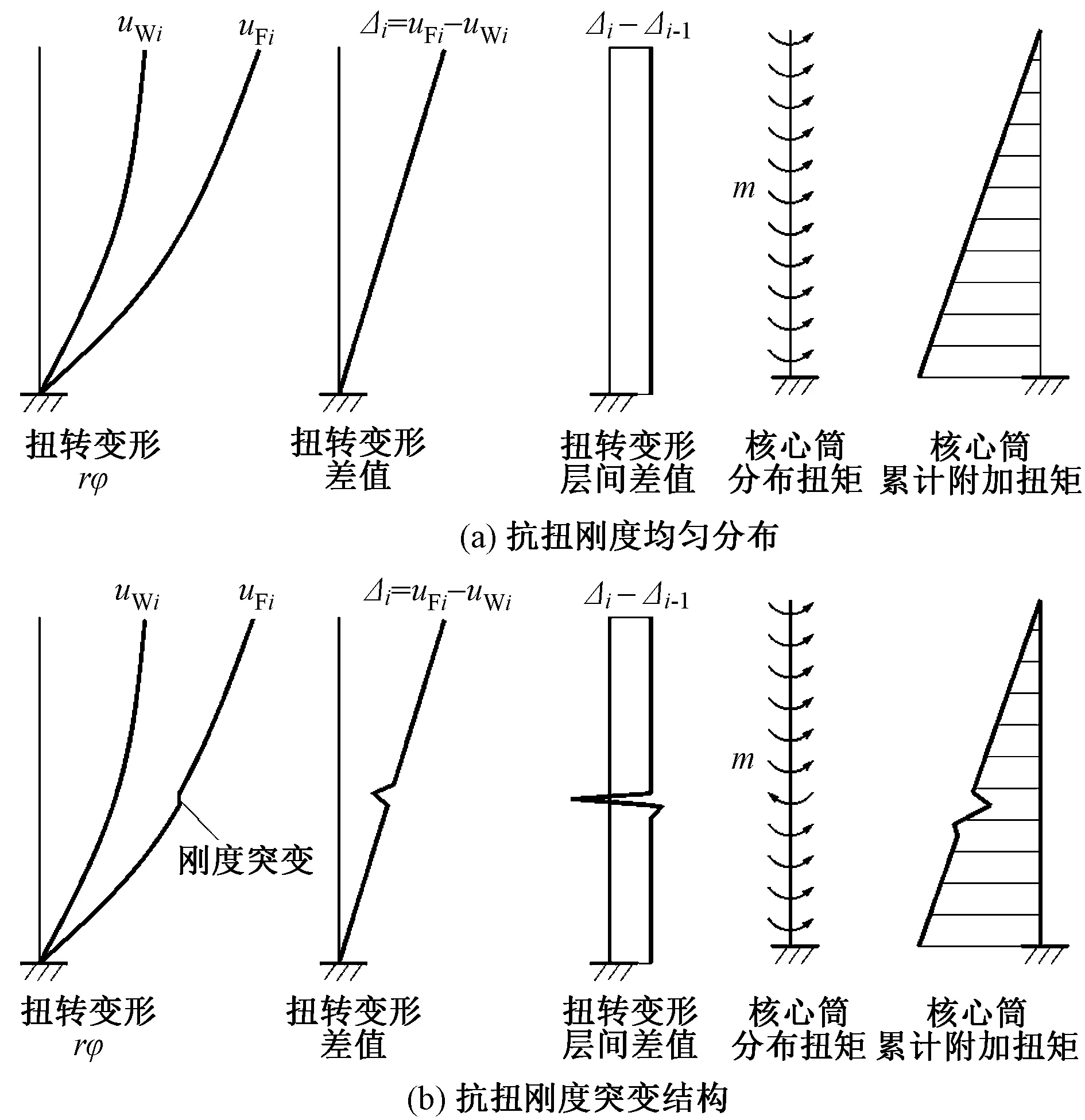
图20 核心筒附加扭矩的形成
根据上述分析,核心筒或外框的抗扭刚度突变(即核心筒与外框的抗扭刚度比)都会引起核心筒扭矩的变化,当外框的抗扭刚度增大时,核心筒的附加扭矩减小;当核心筒的抗扭刚度增大时,核心筒的附加扭矩增大,这与式(3)的计算公式相符。
2.4 增加伸臂桁架
在结构30层和60层增加伸臂桁架,桁架腹杆截面为H800×400×20×30,伸臂桁架的布置如图21所示。
图21 伸臂桁架布置图
增加伸臂桁架前后,竖向荷载作用下核心筒的附加扭矩如图22所示。由图22可知,增加伸臂桁架后,桁架所在楼层核心筒的附加扭矩突然增大,且伸臂桁架所在楼层越高,核心筒附加扭矩的增大量越明显;其余楼层的核心筒附加扭矩均有不同程度的减小,附加扭矩的最大值减小约5%。
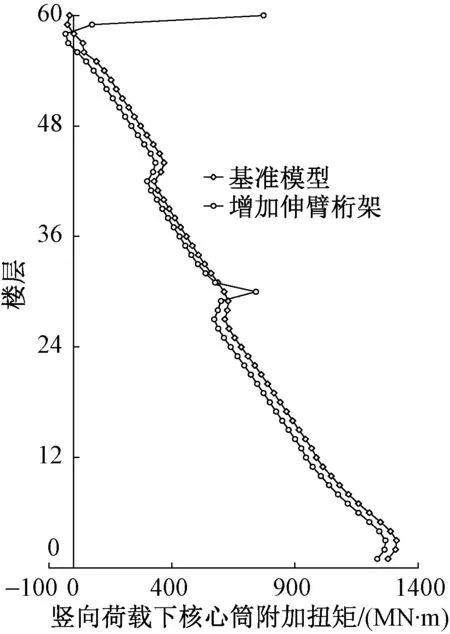
图22 伸臂桁架对核心筒附加扭矩的影响
高层结构中的伸臂桁架能够协调核心筒和外框柱的变形,使两类构件共同工作。伸臂桁架引起扭矩的过程如图23所示。在竖向荷载作用下,核心筒与外框柱的刚度差异引起二者的竖向沉降差,进而使伸臂桁架的上下弦杆产生附加轴力,如图23(a)所示。对于扭转体型结构,伸臂桁架一般不与核心筒外墙垂直,因此桁架弦杆的轴力会引起新的附加扭矩,如图23(b)所示,由于伸臂桁架上下弦杆的轴力符号相反,其所在楼层的扭矩方向也相反,如图23(c),(d)所示。
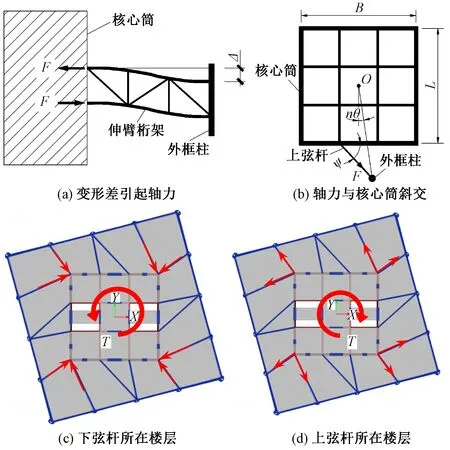
图23 伸臂桁架对核心筒的扭矩作用
在ETABS模型中,对外框柱施加向下的竖向沉降荷载,得到核心筒的附加扭矩分布如图24所示。由图24可知:1)伸臂桁架所在楼层的核心筒附加扭矩都会突然增大;2)伸臂桁架上、下弦杆所在楼层对核心筒的附加扭矩作用大小基本相同,方向相反;3)伸臂桁架所在楼层越高,其对核心筒附加扭矩的影响越大。
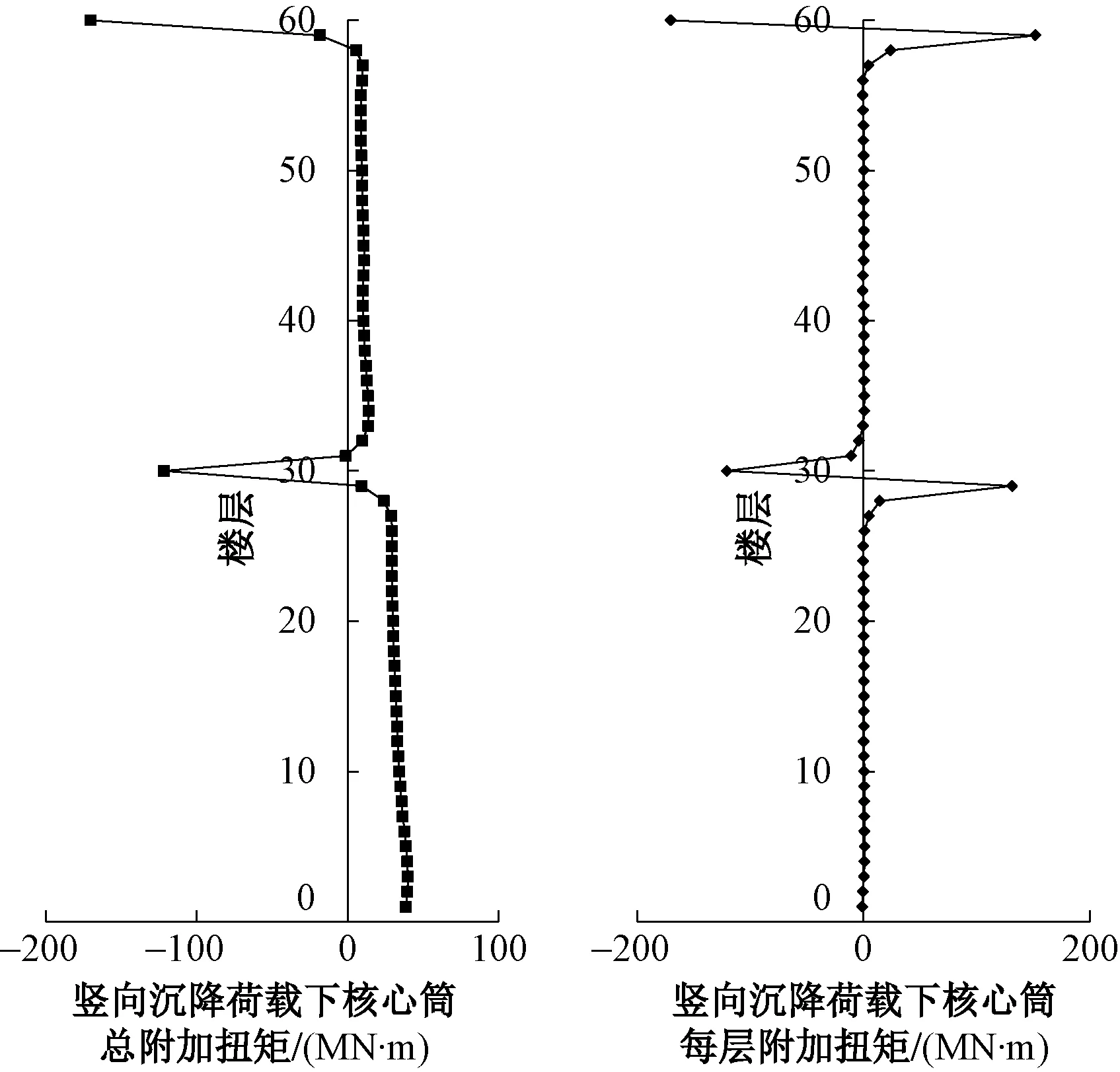
图24 不均匀沉降引起的核心筒附加扭矩
虽然伸臂桁架对核心筒的附加扭矩有一定的影响,但是在实际设计中不宜将其作为减小附加扭矩的一种措施。主要原因为:1)不同结构的内外筒沉降量不同,设置伸臂桁架后核心筒附加扭矩可能增大,也可能减小;2)高层结构的内外筒沉降差对结构本身有不利影响,一般都会通过施工先后顺序来消除沉降差[10]。
3 结论
(1)竖向荷载作用下,扭转体型结构由于斜柱的水平分力使外框产生扭转变形,核心筒为了限制变形而产生与变形方向相反的附加扭矩。
(2)核心筒附加扭矩主要与竖向荷载G、楼层转角θ、旋转半径r、层高h、核心筒抗扭刚度kC和外框抗扭刚度kF相关,且核心筒附加扭矩随楼层转角θ、旋转半径r、核心筒抗扭刚度kC和竖向荷载G的减小而减小,随层高h和外框抗扭刚度kF的增大而减小。
(3)增加反向斜撑可以有效地减小核心筒附加扭矩,当斜撑与斜柱的轴向刚度比满足一定条件时,核心筒附加扭矩达到最小值。
(4)增加中柱对核心筒附加扭矩的影响很小,甚至可能增大附加扭矩。
(5)环形桁架会明显地减小环形桁架所在楼层的核心筒附加扭矩,对其余楼层影响较小。
(6)伸臂桁架会明显改变伸臂桁架所在楼层的核心筒附加扭矩,但不建议将伸臂桁架作为减小核心筒附加扭矩的措施之一。

