浅谈《理论力学》习题的多变性和灵活性
李云涛
(中国石油大学(北京) 北京 102249)
1 研究背景与意义
《理论力学》是机械类等工科专业的基础课程,为学生学习后续课程如《材料力学》《机械设计基础》等奠定了必要的基础。《理论力学》具有科学严密性和应用灵活性,可以很好地培养学生逻辑思维能力、抽象简化能力、实践应用能力。
《理论力学》的学习需通过一定量的习题训练才能熟练掌握。目前国内高校普遍采用的教材大多较为经典,市面上已出版多本针对各类教材的课后习题解答。学生极易在文库等网络资源中找到课后习题答案,致使作业抄袭的现象较为普遍。但是,《理论力学》的习题一般具有多变性和灵活性的特点,基于此,教师可以对一些经典习题做出些许变化,或对解题方法做出必要的要求,并以“雨课堂”等网络辅助教学手段推送给学生,在一定程度上可以避免学生不加思考而抄袭作业的现象。
2 习题的多变性和灵活性
《理论力学》习题的多变性体现在,对于同一道题目,可以通过些许的变化,使题目的求解过程和答案发生较大变化,即“一题多变”。例如,对于一些机构,可以增加约束使其成为静力学问题;或是对于一些结构,可以解除部分约束使其成为运动学/动力学问题。当然,也可以改变主动力的作用位置等,对题目做出修改。这样做的好处是在有限题目的基础上,通过对课后习题的变形,将其转化为一道独特的题目,学生很难在网络上搜索到答案。即使搜到原来的题目,也需要加以思考,在充分理解的基础上,对变化后的题目做出解答。当然,如果学生直接抄袭原题解答,在批改作业时也能一眼识别。这就在一定程度上避免了抄袭作业的现象。
《理论力学》习题的灵活性则体现在,同一道题往往有不同的解题方法,即“一题多解”。以动力学题目为例,通常可以采用“动能定理”,或是“动量定理+动量矩定理”,又或者是“达朗贝尔原理”等多种不同的方法作答。而在对动力学题目做运动学分析时,又可以通过点的合成运动,或是对全局运动方程求导等多种方式进行求解。在使用动量矩定理时,也可以对定点取矩,或是对质心取矩,又或者是对瞬心取矩(当瞬心与质心的距离始终不变时)。这样组合起来,每道题就会呈现出更多的解法。而网络上搜到的题目答案,往往只是一种方法,若要求学生采用多种方法求解,那么也能在一定程度上避免抄袭作业的现象。
以下通过一道非常简单的例题加以体现。
3 典型示例
如图1(a)所示,将一个长度L,质量m的均质直杆AB(梯子)置于墙角。现在,我们增加一些条件,使该题目分别变为静力学问题和动力学问题,并通过多种不同方式对其中的动力学问题进行求解。
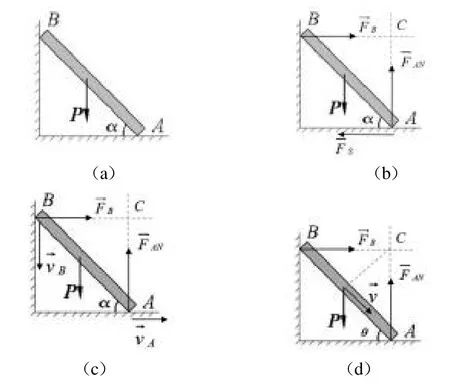
图1:题目示意图(a)原题(b)受力分析图(静力学问题)(c)受力分析图及速度分析(动力学问题)(d)质心速度(功率方程)
3.1 题目的多变性示例
如果AB杆处于静止状态,则该题为考虑摩擦的静力学问题。此时,该题目设置为:假设墙面光滑,地面粗糙,并已知梯子与地面的静滑动摩擦因数为f,求梯子与水平面夹角 的最小值。
对于该问题,分析时首先绘出受力图,如图1(b)所示,包括重力P,A点的法向力FAN,摩擦力FS,B点处的法向力FB。将库伦摩擦定律作为补充方程,建立FS和FAN的关系,进而建立力系平衡方程求解。当然,一种简便的方法是对FB和FAN的交点C取矩,可一步求解出摩擦力FS,此处不再赘述。
还是图1(a)所示的梯子,若假设墙面和地面均光滑,则AB杆将做平面运动,当AB杆与水平面夹角 时,由静止释放,求释放瞬时AB的角加速度。
如此简单的变化,该题由静力学问题转变为动力学问题,求解过程变得完全不同。分析该问题时,首先仍是绘出受力图。由于地面光滑,如图1(b)所示的受力图中应删去FS,如图1(c)所示。此类动力学问题的求解,可采用动能定理、“动量定理+动量矩定理”等多种求解方式,具体求解思路在3.2中进行阐述。
图1(a)所示的场景,不仅仅能变化成上述的两种题目。例如,同样是静力学问题,可以假设墙面与壁面均粗糙,并已知两处的静滑动摩擦因数,求梯子与水平面夹角的最小值。这样就变成了存在两处摩擦的平衡问题。又例如,对于动力学问题,可以假设AB杆在下落的过程始终与墙面相接触,求即将落地瞬间AB杆的角速度,以及A点的受力。这样不仅考察了动能定理,同时还考察了动量定理和动量矩定理,以及平面运动中求一点加速度的基点法,题目变得更加综合。
3.2 题目的灵活性示例
若墙面和地面均光滑,要求解AB杆由静止释放时的角加速度,则可通过多种方法实现。
方法一:动能定理。假设下降任意时间后,AB与水平面夹角为 ,如图1(d)所示。对于做平面运动的刚体AB,动能一般表示为随质心平动的动能和绕质心转动的定能之和。此时需要表示出质心的速度。而事实上,平面运动刚体动能的表达式,是由绕瞬心做定轴转动刚体的动能推导而来,因此,动能可表示为T=0.5Jc2,其中 是角速度,Jc是AB杆对瞬心的转动惯量,通过平行轴定理可求得为1/3 mL2。由动能定理可知,动能的增加量等于重力做的功即T=0.5mgL(sin-sin)。因此,对等式0.5mgL(sin-sin)=0.5 Jc2的等号两边同时求导,并令 = ,即可求出AB杆在释放瞬时的角加速度。
方法二:功率方程。同样假设下降任意时间后,AB与水平面夹角为 ,此时重力做功的功率为mg·v。其中,v是AB杆质心的速度矢量,其大小为0.5 L。由几何关系知速度v和重力mg的夹角为 ,如图1(d)所示。由功率方程,功率mg·v=0.5mg Lcos等于动能T=0.5 Jc2对时间的导数,题目得解。
方法三:动量矩定理(对质心取矩)。采用该思路的一般解题方法,都是建立质心运动定理和对质心的动量矩定理来求解,同时还需根据已知的A点和B点加速度方向,通过基点法建立AB杆角加速度与质心加速度的关系。对于该题而言,此种解题方法较为繁琐,此处不再赘述。
方法四:动量矩定理(对瞬心取矩)。在刚体平面运动的过程中,若瞬心与质心的距离始终保持不变,则可对瞬心使用动量矩定理。该题目中,瞬心与质心的距离始终为0.5L,满足定理的使用条件。由于A、B两点受力均通过瞬心C,其矩为零,通过对瞬心的动量矩定理可直接列出角加速度与重力之间的关系。相对其他方法而言,该方法仅通过一个方程求解,最为简单。
当然,该题目还可采用达朗贝尔原理(动静法)求解。可见,《理论力学》习题的解题思路较为灵活,在教学过程中可以引导学生尝试不同的解题技巧,加深学生对于知识点的理解和掌握,同时也能更好地培养其逻辑思维能力。
4 结论
《理论力学》习题具有多变性和灵活性。多变性体现在,对于同一道题目,可以对受力情况做些许变化,使题目的求解发生较大变化。灵活性体现在同一道题往往可以有不同的解题思路。本文通过一道简单的例题对这种多变性和灵活性进行了说明。该题目做出些许变化,即可由静力学问题转化为动力学问题。针对该简例的求解方法,可以覆盖平面任意力系平衡方程、考虑摩擦的平衡问题、平面运动、动量定理、动量矩定理、动能定理以及达朗贝尔原理等多个知识点,具有很强的综合性。在日常教学中,将题目加以变化或是要求学生采用多种解题方法求解,可以有效避免学生通过网络搜索答案并不加思考直接抄袭的现象。

