基于曲率约束的服装工业样板分割线提取方法

蔡晓秋

(黎明职业大学 新材料与鞋服工程学院，福建 泉州 362000)

近年来，随着计算机技术的发展和三维扫描仪器的广泛应用，扫描得到的几何细节层次特征更加丰富[1-2].同时，由于扫描规模的扩大和三维数据量的增加，传统几何表示方法的局限性也越来越明显.相关专家对服装工业样板分割线提取做了大量研究，张晶等[3]通过投影轮廓匹配策略对文本进行涂抹确定文本数量，在设定的方向上进行动态规划，搜索最小能量线，结合中线区约束获取最佳分割线，最终实现提取.黄锦洲等[4]首先利用不同边缘点误区匹配不同的特征点，再通过基于灰度相关的边缘点分类匹配方法进行计算获取点云数据，结合边缘曲率概念快速实现轮廓信息提取.上述两种方法虽然取得了非常满意的研究成果，但仍不能满足现阶段的发展需要，为此，提出了一种分割线提取方法.仿真结果表明，所提方法能够准确提取服装工业样板分割线.

1 曲率估计

1.1 数据预处理

为了简化曲率估计流程，采用p={pi}表示采样的三维点pi组成的一个点集，∏(pi)={qi,1,qi,2,...qi,k}表示采样点pi的k最近邻域点，与网格曲面点样本之间没有明显的拓扑联系信息[5]，因此无法确定样本点的邻域点，主要用于估计邻域点的微分属性.

在点采样曲面中网格曲面的几何连接信息能够通过k最近邻域点转换获取.通常情况下，初始曲面的近似值是通过对初始曲面进行密集采样得到的，因此只要选取适合k的值，采样点将不会存在较大的误差.在实际应用中，Kd-Tree的数据结构可以通过点采样曲面建立，使其能够快速找到采样点k的领域.

虽然三维数据采集设备日趋完善，精度也在逐步提高，但还是会受到测量方式和人为因素的影响，采样数据不可避免的有或多或少的噪声和误差[6]，会出现区域重叠或者数据过于稀疏的情况，为了提高点采样曲面对原始曲面近似表示的可靠性，需要对原始曲面模型或其他后续处理的几何微分性质进行精确估计，例如简化、曲面重构等.通常给采样数据点pi赋予一个权重wi，其中，权重是一个高斯核函数，表示如下：

wi=e-ai/r2.

(1)

上式中，wi代表权重取值；ai代表拟合系数；r代表二次曲面系数.

1.2 移动双三次B样条曲面

当获取到采样点pi的邻域点集∏(pi)时，利用邻域点集提供的局部信息来估计pi微分性质.一般来说，二次函数可以定义为pi的邻域设定点，此过程与估计网格曲面中顶点的曲率过程相同[7]，最后利用拟合的二次曲面来估计pi的曲率.这里不是简单地采用二次函数，而是利用双三次B样条曲面拟合.双三次B样条曲面具有许多优良的性质和相对简单的计算形式.因此，它被广泛应用于离散数据、图形等领域的插值和逼近.双三次B样条曲面曲率计算式为：

(2)

公式(2)中，Q(u,v)代表曲率估计值；Bi,j代表曲面控制点；Ni,k(u)代表u方向上对应的三次样条基函数；Mj,l(v)代表v方向上的三次样条基函数，其表达形式如下：

(3)

(4)

其中，Mj,l(v)所表示的含义与Ni,j(u)相似.

在用最小二乘法拟合双三次B样条曲面的过程中，需要针对每个采样点进行参数化处理，将平面投影参数转化为点集的邻域，并将所有点的尺度全部放到[0,1]×[0,1]平面上，然后得到每个采样点对应的ui,vi.依据公式(5)获取双三次B样条曲面的定义如下：

(5)

公式(5)中的各个字母分别代表不同的采样点参数值.

1.3 曲率计算

微分几何中，设定曲面上一点为正交的共轭方向，即曲面的主方向，主方向上的法曲率称为曲面的主曲率.当曲面上某一点的曲率向曲面的各个方向选择曲率最大值kmax和最小值kmin时，则kmaxkmin积曲面高斯曲率称为点kg，其平均曲面曲率(kmax+kmin)称为点km.

通过对双三次B样条曲面进行小方拟合[8-9]，利用公式(2)的偏导数可以得到采样点的各阶导数，其中经过偏导处理的结果如下：

(6)

上式中，Qu(u,v)代表导数偏导处理结果.

然后，利用公式(6)和曲率微分几何理论，计算曲面上任意点的高斯曲率和平均曲率：

(7)

(8)

上式中，kg代表高斯曲率；km代表平均曲率；B、M和S均代表不同曲率微分几何参数；Qv和Qv分别代表不同阶的导数.

当R=[Qu×Qv]·[QuuQuvQvv]，主曲率可由高斯曲率和平均曲率进行计算：

(9)

上式中，k1代表主曲率.

1.4 点采样的选取

在样点曲面中，点邻域中采样点pi的个数k是一个重要的参数，如果k值太小[10]，无法全面反映原始曲面的局部特性；如果k值太大，则局部特性的表现和计算量无法得到充分增加.当所有采样点使用相同的k值时，噪声和无噪声采样点能够估计对k值的影响，选择k值计算公式的缺点是方法过于复杂，需要反复迭代才能得到一个好的k值.对于样品表面，均匀点根据不同的取样给出上下密度k的值，认为k值足以反映原始表面3≤k≤50的局部性质，这也表明当k值在6～25之间时，可以准确给出k的上下限，因此k取值范围是16≤k≤25.

2 三维网格模型凹区域的提取

2.1 三维网格模型凹区域

根据微分几何，凹凸曲面的高斯曲率取决于点k曲率和平均曲率点H.任意点可分为(k<0)、抛物线(k=0)、双曲点和椭圆[11-12].由于噪声的存在，导致散射顶点本身无法确定研究区域，因此单纯考虑凹凸性.根据每个顶点面积的高斯曲率和平均曲率来确定凹凸性符号的面积.

(1)凸区域.如果顶点与高斯曲率域中的一个顶点同时到达，则该区域为凸区域.

(2)凹区域.如果顶点及其相邻顶点的高斯曲率为负，则该区域是凹的.

(3)脊面片区域.如果一个顶点和它的域顶点的一边是高斯曲率零点，一边是平均曲率正点，并且共享边的三角形法向量之间的夹角超过一定值，则该区域是背面区域.

(4)马鞍区域.如果平均曲率和高斯曲率的顶点及其相邻顶点为负，说明局部大部分是凹的，小部分是凸的，这个区域是马鞍区域.

(5)平坦区域.如果高斯曲率和平均曲率的相邻顶点均为0，则该点为平坦点，该区域为平坦区域.

2.2 凹区域提取算法

为了找到分割线面积，首先要找到凹面积网格模型，根据顶点的高斯曲率和平均曲率来确定凹面区域的网格.此外，由于离散曲率对噪声的敏感性，在凹面分割中容易产生很好的分割效果.为了进一步反映模型的整体特征和表面凹面区域，根据每个顶点的曲率分布对近场区域和凹面区域进行进一步扩展[13]，删除凹点设置，同时进行区域优化，促使凹区模型能很好地反映区域特征.凹面区域提取算法分为3个步骤：

(1)计算凹面点集.在计算过程中用凹点计算出3D_point中每个顶点的高斯曲率k和平均曲率H，Neil得到每个顶点的邻域节点；如果顶点i的邻域Neil中所有顶点的高斯曲率K和顶点i的平均曲率H满足K<0&&H<0，则顶点i被加到Concave_Region上[14]进行区域延伸，去除目标即优化凹点集，其中凹点区域会在更小的凹面区域后被删除.

(3)区域删除.删除区域内所有连通分量Concave_Region的计算，每个连通分量Vnum_bran计算定点数和连通分量中高斯曲率的平均值Gau_bran，然后找出Gau_bran>threshold2的区域，并在Concave_Region中删除连通分支.

2.3 服装工业样板分割线提取

结合曲率估计进行服装工业样板分割线提取，具体的操作步骤如下：

(1)通过凹区域节点连接形成相近邻域的三角面片区域，计算曲率估计连接边的边权；

(2)凹区域的边分别由外层边界和内部边组成；

(3)每一条边都会有一个权值递增，剔除右最小值的同时，结合细化算法，将该区域细化成一个包含凹凸特征的区域，将所获取的特征曲线设定为分区域划分的分割线，以此实现服装工业样板分割线提取.

3 仿真实验及结果分析

为了验证本文方法的有效性，测试图像来自MNIST数据库.实验的主要目的是测试服装工业样板分割线提取结果的准确性，在数据库内任意选取两幅图像进行分割线提取，对比方法为文献[3]方法和文献[4]方法，具体实验结果如图1～图4所示.

图1 测试对象1

(a)本文方法的服装工业样板分割线提取结果

图3 测试对象2

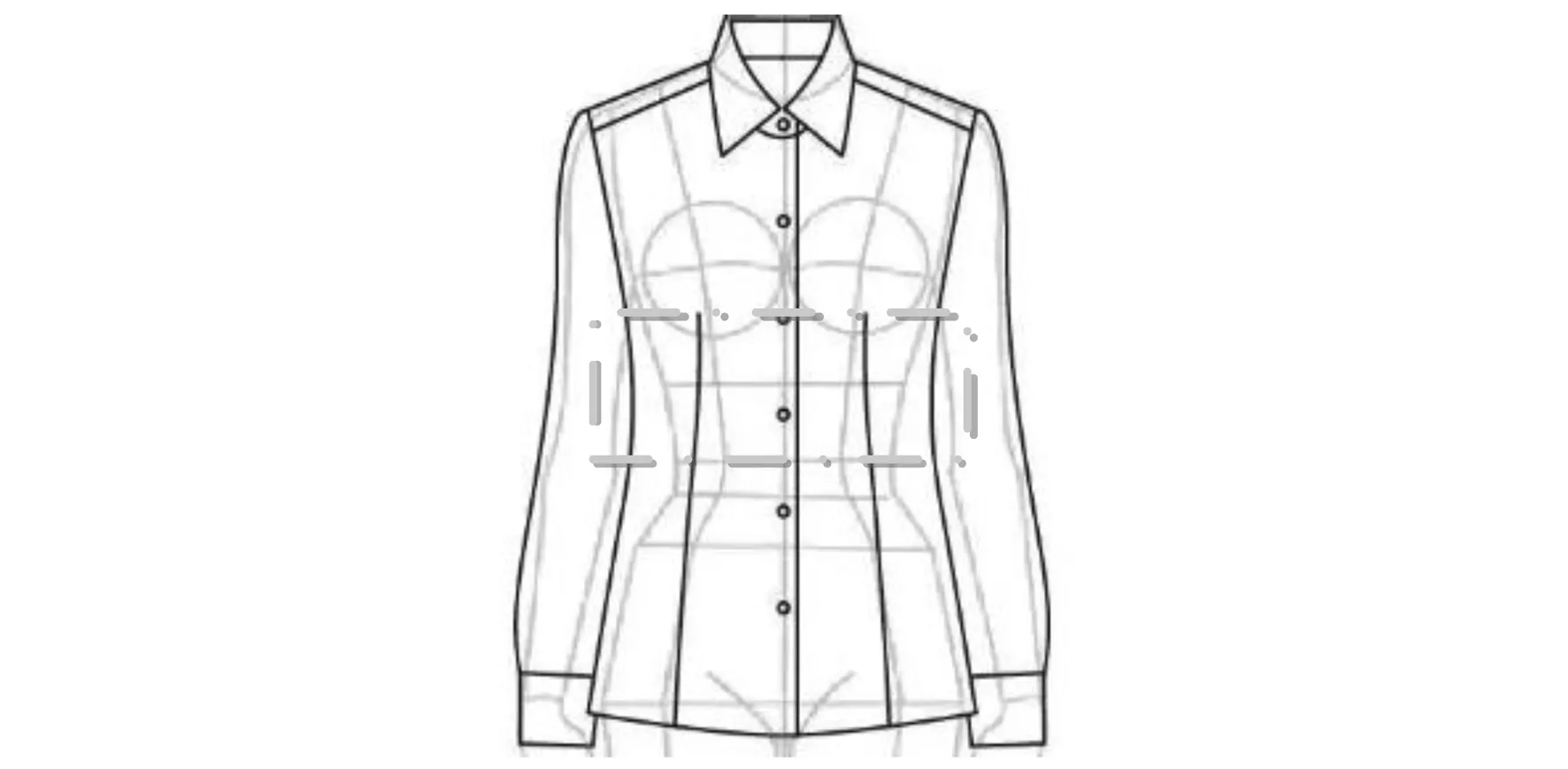
(a)本文方法的服装工业样板分割线特征提取结果

通过实验数据可知，所提方法能够精准提取服装工业样板分割线，有效地显示了分模线角度和片数的变化规律，并有效地降低了曲率约束分割线特征提取偏差对服装行业模板的影响，大大提高了准确率.同时，与其他两种方法相比，该方法具有较低的偏差和较高的精度.

4 结束语

针对传统方法存在的缺陷，提出了一种基于曲率约束的服装行业模板分割线特征提取方法.仿真结果表明，所提方法能够准确提取服装行业模板中的分割线特征.但是由于受时间及环境等多方面因素的限制，致使所提方法仍然存在一定的不足，后续将对其进行进一步完善和改进.