炸药爆炸在固体介质界面的压力计算与分析

刘 伟,郭子如,吴俊浩,杜宝强,刘 锋,何志伟

(安徽理工大学化学工程学院,安徽 淮南 232001)

同固体介质材料中应力波传播演化的关键控制方程一样,在高压冲击下,考虑材料自身物理力学性能,是掌握冲击波在传播演化的关键因素,描述高压状态下材料的冲击响应,就是材料的状态方程[1]。陈熙蓉等[2]以TNT作为爆炸加载,通过实验测量了冲击波在不同材料的隔板中不同位置的到达时间,进而得到隔板不同厚度处的冲击波压力和速度；王海福等[3]根据冲击波在密实介质传播中、前期的衰减特性,从介质温升效应出发,建立了一个近似计算模型,并利用该模型分别对铝、钢和有机玻璃介质中的冲击波衰减特性进行了计算；王远飞[4]在炸药与单层钢板或复合板接触爆炸条件下,测量金属板中的冲击波速度,结合实验结果研究了炸药在金属板中的冲击波衰减规律；韩秀凤等[5]研究了雷管输出冲击波在有机玻璃中的衰减特性；刘好全等[6]通过数值模拟了B炸药对铝、铜介质中爆轰波斜反射现象,得到了不同入射角度下金属材料的动态响应结果,得出了介质分界面处压力随入射角度的变化规律；Mithchell等[7]利用冲击阻抗匹配法,用二级轻气炮加压到20～430 GPa,测量了铝、铜、钽的冲击波压缩性曲线；Wall[8]采用高速摄影方法记录了钢样品中动力层裂传播的实验数据；王翔[9]利用金属状态方程精确测量技术,测量了Cu、Ta、Pt等材料在30～600 GPa压力下的Hugoniot数据,实验测量结果与国外公开发表的数据相比,具有极好的一致性。虽然他们在一定意义上描述了冲击波作用于固体介质的相关特性,但是,接触爆炸时,若采用一种较为准确的分界面爆炸压力理论计算式,即材料状态方程与分界面波后压力方程联立,就可以较为合理地计算冲击波在固体介质分界面的初始爆炸参数。在碎甲战斗部中,估算炸药与钢板分界面爆炸压力,可以分析冲击波作用于钢板后,钢板发生层裂的可能性,对改善碎甲战斗部的作功能力有一定参考意义。笔者在前人研究的基础上,介绍了3种冲击波作用下固体介质的状态方程,以文献中相关条件建立场景,运用这3种状态方程对同一场景进行计算,将计算结果进行分析和比较。

1 一维平面爆轰波理论

假定:①平面爆轰波在分界面上的透反射为一维的；②固体介质的冲击波阻抗大于爆轰产物冲击波阻抗[10]。当爆轰产物绝热方程PVγ=常数时,则分界面处反射冲击波与爆轰波之间有如下方程:

固体介质中冲击波阵面前的压力远小于阵面后的压力,因此,可以忽略。入射冲击波阵面后的介质运动速度ux为:

式中:ux为介质分界面的运动速度；Px为反射冲击波阵面后的压力；Vm0和Vmx分别为冲击波阵面前后的介质比容。

2 冲击波在固体介质中冲击响应

拟介绍3种描述固体介质中冲击压缩规律的计算式。第1种是在凝聚介质中冲击波速度D与其波后质点速度u之间,在相当宽的速度范围(或压力范围为1.7～200 GPa)内存在的线性关系[11]:

式中:D为冲击波速度；a、b均为不同材料的系数值；ux为介质分界面的运动速度。将式(4)代入冲击波动量守恒方程得

式中:ρ0m为介质密度。根据波后质点速度方程(2)与波后压力方程(5),利用作图法可求出炸药与固体介质分界面处的冲击波压力和波后质点速度。

第2种是固体介质中冲击波波速Us与波阵面后的粒子速度Up的线性关系式[1]。假定:①材料在冲击过程中不产生相变；②该材料为密实介质。

式中,S为经验系数。其中,钢的经验系数为1.49,铝的经验系数为1.34,有机玻璃的经验系数为1.52。将式(6)与冲击突跃条件联立形成一个新的控制方程,可以得到Vmx与Px之间的关系:

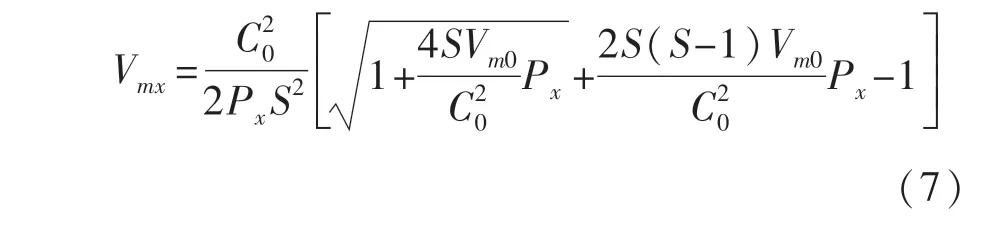
将式(7)代入式(3)得到ux与Px之间的关系,再结合式(2),可利用图解法求出炸药在固体介质分界面处的爆炸压力和质点速度。

第3种是根据材料体积模量K与压力P之间的线性关系:K(P)=K0+nP。其中,n为体积模量对压力的一阶导数在零压下的值,积分得到默纳汉状态方程,适用于等温、等熵、冲击绝热压缩过程[1]。

式中:A=ρm0C20/n；ρm0为固体介质密度；ρ0为炸药装药的密度；n为体积模量对压力的一阶导数在零压下的值,不同的实验者得到的实验值不同,一般取3～4。将式(8)与式(2)联立,利用作图法即可求出炸药在固体介质分界面处爆炸压力和波后质点速度。

3 场景建立与结果分析

场景1:文献[4]选用密度为1.777 g/cm3,ø100×50 mm的钝化RDX炸药药柱,采用1985年吴雄提出的ω-Γ公式计算得到钝化RDX炸药的爆速为8.668 km/s,爆压为34.178 GPa。绝热指数为2.980 6。利用光纤探针技术,实验测量钝化黑索金与钢板接触爆炸条件下,冲击波到达靶板中不同位置的时间,得到炸药在钢分界面冲击波压力为37.62 GPa。

场景3:文献[11]选用长度为50 mm,直径为45 mm的PETN/TNT(质量比50∶50)药柱,密度为1.57 g/cm3,采用ω-K法计算得到炸药爆速7.351 km/s,爆压为22.24 GPa,绝热指数为2.81。利用锰铜压力计测试法,得到药柱与有机玻璃隔板界面处冲击波压力值为15.62 GPa。固体介质相关参数见表1。

表1 固体介质相关参数

对于场景1,炸药在钢板分界面上采用第1种固体介质冲击压缩规律计算式,式(4)变为:

将式(11)与式(10)联立,利用作图法如图1所示,得到炸药在钢板分界面爆炸压力与波后质点速度为:Px=52.98 GPa,ux=1.16 km/s。同理,采用第2种、第3种固体介质冲击压缩规律计算式,得到炸药在钢板分界面的爆炸压力为52.94、39.69 GPa。按照上述计算方法,可以得到炸药在铝和有机玻璃分界面上的爆炸压力值,计算结果见表2。

图1 低碳钢界面处冲击波初始参数

通过分析可以看出:

1)3种状态方程从不同角度出发得到了冲击波在固体介质的冲击响应,第1种和第2种状态方程本质是描述固体介质中冲击波速度D与其波后质点速度u之间的关系,虽然取的常数值(a、b和C0、S)不同,但计算结果相近。3种状态方程本质上都是固体介质中冲击波后压力P与介质密度ρ之间关系的近似表达,为经验计算式。

2)根据3种冲击波在固体介质中的冲击压缩规律计算式,结合冲击突跃条件式,计算得到炸药在固体介质界面处爆炸压力值满足如下关系:状态方程1＞状态方程2＞状态方程3＞文献实验值,状态方程3(即默纳汉状态方程)更适合描述冲击波在固体介质中的冲击压缩规律,第3种状态方程得到的计算结果与实验值更为接近。