基于ABAQUS的网捕无人机动力学仿真分析

魏远旺，杜忠华，陈 曦，马瑞雪，史文辉

(南京理工大学 机械工程学院， 南京 210094)

1 引言

近些年来，随着国家对低空领域(飞行高度低于1 000 m的空域)的开放，无人机行业以前所未有的速度迅猛发展，并在全球范围得到了广泛应用。数据显示，全球无人机2015年的销量约58.7万架，其中97%为民用无人机，而民用无人机销量中约有39.9万消费级无人机[1]。无人机已经成为迅猛增长的新兴产业，广泛应用于航拍摄影、灾难救援、遥感测绘、环境监测、地质勘探、农业等各个领域。

调研表明，目前国内已经超过400家企业从事无人机的研制，但从事无人机安防的企业却寥寥无几[1]，监管反制手段的脱节、相关领域法律法规尚不完善，导致各种无人机“黑飞”现象频见报端。

网弹式拦截是目前无人机安防领域的热点方案之一[2-3]，其主要原理是通过对目标无人机发射网弹，并在与目标交汇位置实时开仓抛射飞网，折叠放置在网仓内的柔性绳网在牵引体惯性作用下拉伸展开，逐渐与目标接触碰撞，当网展开到最大极限时，由于自身弹性牵引体开始反弹导致柔性网收缩，并在牵引体的甩动缠绕下完成对目标的抓捕。

由于柔性绳网在执行捕捉任务中具有较大的容错能力，国内外许多学者对绳网捕捉类系统的动力学建模进行了广泛研究和讨论，赵国伟等[4]将网格离散为有限质量节点-杆单元模型，质量分别集中于节点和杆单元的中心，两者的相互作用力与节点与杆单元中心距离有关；Provot[5]将网目简化成质点-弹簧模型，质点与质点之间用弹簧相连，用弹簧的拉伸来模拟网的拉伸展开状态而建立起网系统的动力学模型；陈钦等[6]将柔性网简化为由多个质点-弹簧阻尼单元连接而成的多体系统动力学模型。综上可见,质量集中法是应用较为广泛的绳网类系统建模方法[7]，然而，虽然这类方法能够一定程度上反映柔性网的动力学特性，但由于实际柔性网在飞行展开过程中主要通过自身弹性变形来传递运动和力，网体在力的作用下有很大变形，内部单元相对之前折叠状态有较大的非线性位移和角位移，且这类方法未考虑网绳不受压的特性，因此在此基础建立的柔性网模型中研究网收缩时存在一定偏差。

本文在对比以上模型的基础上，根据绳网受拉不承压的力学特性，建立质点-Truss单元柔性绳网的有限元模型，将每段网绳离散为无限段极小的绳段单元，每小段绳段单元等效成“不考虑剪切扭转变形、只承受轴向拉力而不受压”的弹簧阻尼模型，对其动力学特性进行分析，而后在ABAQUS软件中，采用Truss单元模拟网绳，建立柔性网捕无人机的有限元模型，对柔性网的折叠展开以及捕捉目标的动力学过程进行仿真模拟分析。

2 柔性网捕系统动力学建模与设置

2.1 柔性网绳动力学建模

高柔性绳网系统属于缺乏约束的大变形柔性系统，一直是非线性仿真中研究的难点。一是比较难建立精确的数学模型，且因其属于非线性问题不满足叠加原理，无法得到解析解；二是大变形柔性系统缺乏约束，导致求解过程经常出现收敛困难[8]。

为了建立比较合理的柔性绳网模型，应对网绳的特性进行分析，除编织柔性网的材料非线性外，其最主要的力学性质是网绳只能承受拉力而不受压，这一特性将引起柔性网在展开过程中不同时刻的状态、响应、几何、接触均是非线性的，在综合分析绳网系统的非线性特点基础上，根据有限元原理将网绳离散成一段段绳段单元，每段单元看成是“受拉不受压”的弹簧阻尼模型，如图1所示。

图1 绳段Truss单元示意图

绳段ij两端点分别表示节点i和节点j，则绳段ij之间的张力Tij大小为：

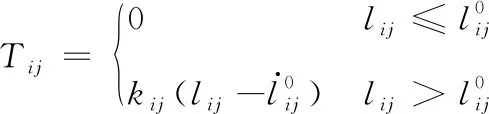
(1)

(2)

(3)

式(2)、式(3)中：E为网绳的弹性模量；Aij为绳段ij单元的的横截面积；ξ为阻尼比；mij为绳段ij单元的质量。

绳段ij单元的当前长度lij与变化率表示为：

lij=||rj-ri||

(4)

(5)

式(4)、式(5)中：ri和rj表示绳段ij单元两端节点在图1所示惯性坐标系下的位置矢量；eij表示方向由节点i指向节点j的单元矢量。

2.2 柔性网捕系统有限元建模

非线性有限元软件ABAQUS采用显式方法求解动力学仿真方程,在材料非线性、几何非线性(大位移、大应变和大转动)等复杂问题的求解上独具优势，本文采用ABAQUS/CAE模块建立网捕无人机的有限元模型，该模型研究的柔性网形状呈正方形，展开尺寸1.2 m×1.2 m，网孔规格为30 mm×30 mm，质量为1.65 kg，4个角点各系一个牵引体，如图2所示。

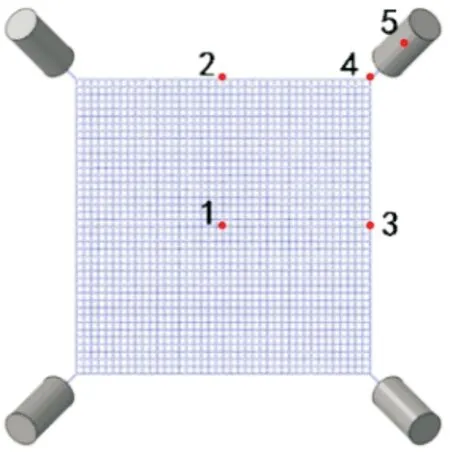
图2 柔性网有限元模型示意图

研究表明，通过对柔性绳网类结构有规律地折叠放置，不仅能够在发射过程中获得更好的稳定展开效果[9]，还能有效减小发射装置的空间尺寸。折叠方式多种多样，Gärdsback等[10]对网的折叠方式和网格构型进行了研究，重点通过对三角星、四角星的折叠方式进行对比探讨，指出可行的折叠方式是飞网成功展开的关键。由于发射前需要将其存储在较小空间的网仓内且要保证网绳不会发生相互缠绕导致展开困难甚至无法展开，本文采用“V”字型折叠方式，即对每小段网格单元均进行“V”型对折，如图3所示，经过折叠后的柔性网投影尺寸为40 mm×40 mm，显然在更大程度上减小了柔性网所占网仓空间。

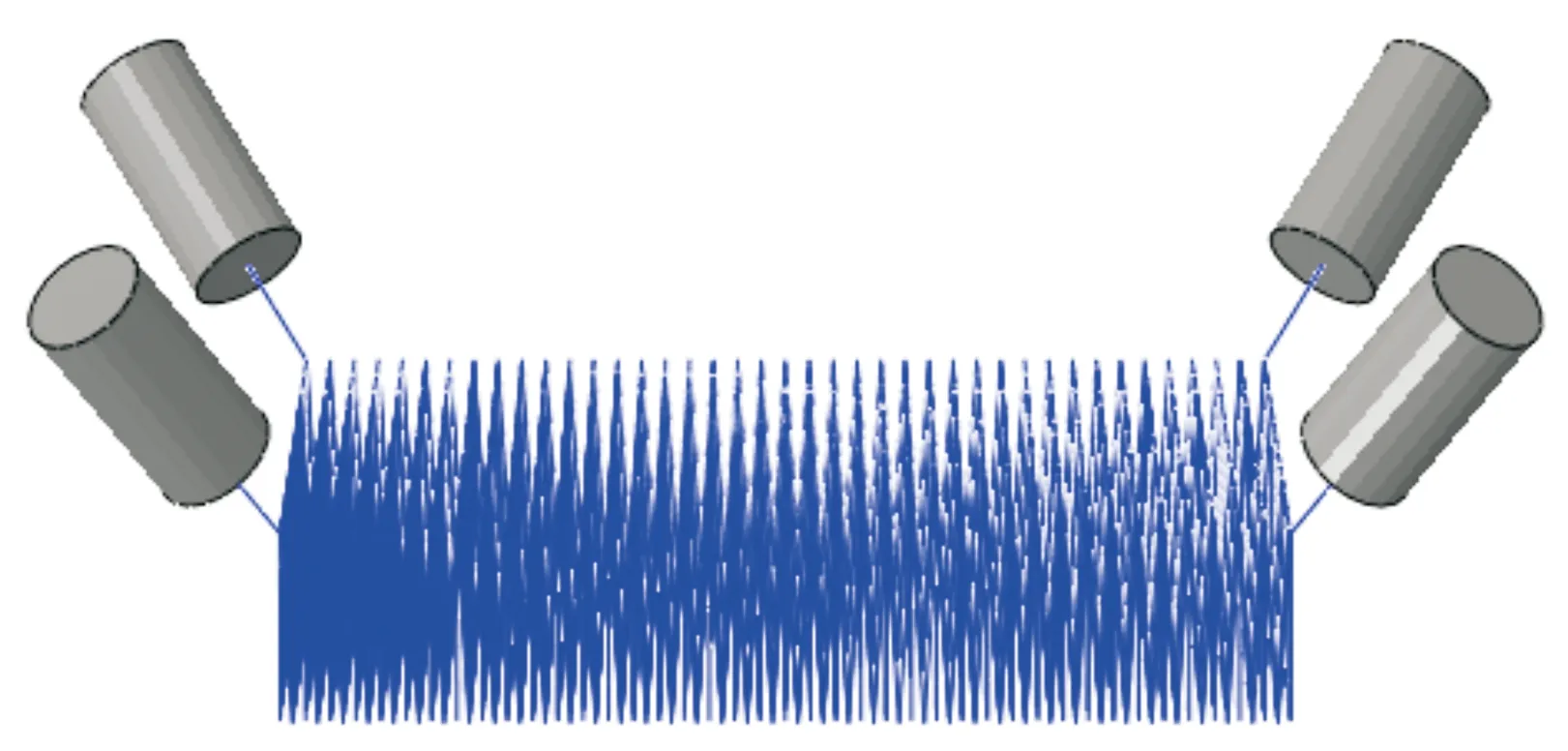
图3 “V”字型折叠的柔性网有限元模型示意图

无人机的建模以大疆的御Mavic Pro型号四旋翼无人机参数指标为参考，尺寸为83 mm×83 mm×198 mm，重量0.74 kg，本文重点研究柔性飞网的展开与捕捉目标效果，故无人机建模只画出大致形状，最终网捕无人机有限元模型如图4所示。

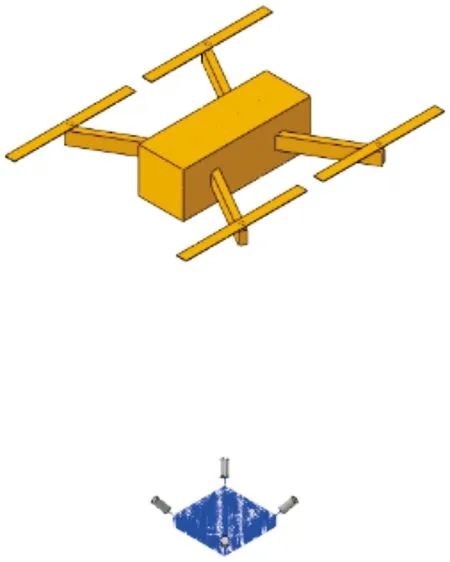
图4 网捕无人机有限元模型示意图

2.3 仿真要点与参数设置

在ABAQUS有限元模型中，柔性网绳采用Truss单元类型来模拟，牵引体采用三维实体单元模拟，两者通过建立相关节点的绑定约束可以真实模拟牵引体与绳网之间的相对状态，在此基础上设置仿真对象的材料等属性，得到有关仿真参数如表1所示。

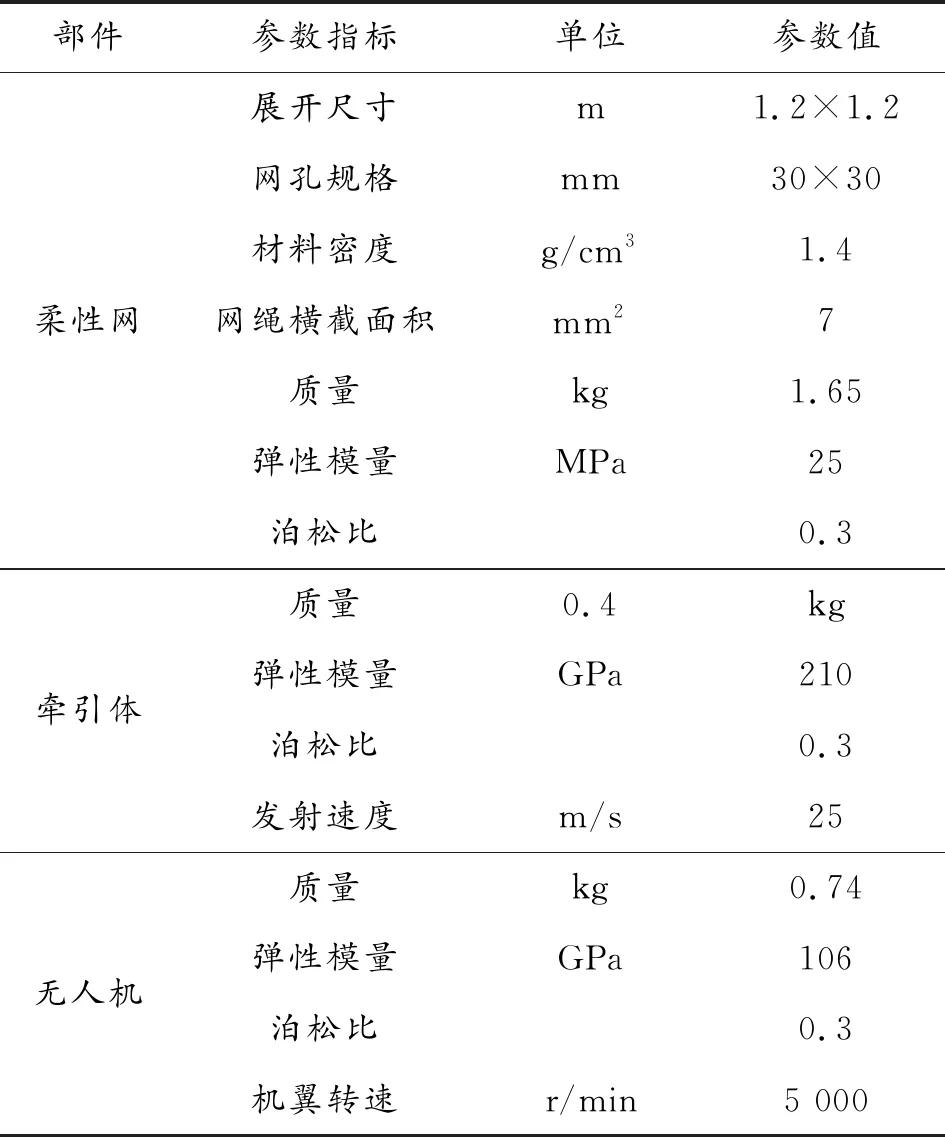
表1 仿真参数指标

网捕系统在仿真展开过程中主要受到牵引体的牵引力、重力、空气阻力、网绳互相拉伸的弹性内力等影响，重力施加在整个系统模型中，牵引力通过以一定初速度发射的牵引体产生，空气阻力在ABAQUS中可以通过建立流场来模拟，也可以转化为相关阻尼来近似模拟计算，本文采取后一种方式。此外，本文不重点研究无人机、牵引体的应力变化，故将无人机、牵引体简化为刚体来处理，可以有效降低仿真计算的复杂度与开销。

由于网绳线径远小于无人机尺寸，如果两者之间的接触关系处理不好，在计算过程中将出现“接触穿透”问题甚至是不收敛的情况。在ABAQUS仿真中采用罚函数建立网体的自接触、网绳边对无人机表面的接触，这样当网展开撞到无人机时，绳网只能沿无人机表面的切向进行表面滑动，而不是沿法向嵌透穿入无人机机体内部。而一旦绳网节点与无人机节点开始出现穿透，基于罚函数法建立的接触面之间会引入相对较大的法向接触力来防止网与无人机之间进一步穿透，该方法能够解决绝大部分绳网与无人机之间的接触穿透问题，其中法向接触力可以通过“弹簧弹力”来描述，表示为：

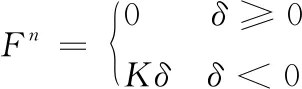
(6)

式(6)中：K为罚刚度；δ为接触穿透深度。

由库伦摩擦定律可得切向接触力，表示为：

Fτ=μFn

(7)

式(7)中，μ为网与无人机之间的摩擦因数。

在显示动力学仿真分析中，阻尼主要用于阻止非真实振荡，直接影响系统最终能否趋于稳态[12]，网捕系统结构阻尼矩阵C是质量矩阵M和刚度矩阵K的线性组合(如式(8)所示)，它描述了柔性绳网在拉紧和松弛过程中通过阻尼方式消耗能量的比率[6]。

C=αM+βK

(8)

式(8)中，α和β分别为质量矩阵和刚度矩阵的阻尼系数，本文仿真实例取α=5，β=4.8×10-6。

3 仿真结果与分析

以图4网捕无人机有限元模型和相关参数设置为基础，对柔性网捕无人机过程进行动力学仿真分析计算，仿真时间为1 s，对称分布的4个牵引体的发射角度θ均为45°，发射速度v为25 m/s,得到其动态展开状态仿真结果如图5、图6所示(分别为等轴测图和侧视图)。

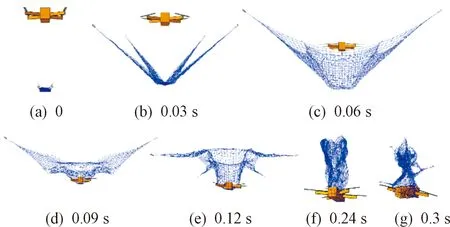
图6 网捕无人机动态过程仿真侧视图

由仿真结果可知，柔性网初始状态处于折叠松弛状态，随着牵引体的发射飞行对网进行拖拽而产生牵引力，折叠网在牵引力与网绳之间的弹性内力作用下逐渐拉伸展开，直至柔性网完全展开呈类抛物面状，而后与捕捉目标交汇碰撞，绳网达到最大拉伸状态后，由于网绳自身的弹性，牵引体开始逐渐反弹而使柔性网收缩，并随着牵引体的甩动缠绕将目标无人机完全包裹，最终在0.3 s左右完成对目标的捕获。

选取图2所示关键节点1(网中节点)、2(上弦中节点)、3(右弦中节点)、4(网角节点)、5(牵引体)进行研究分析，得出其位移、速度分别随时间的变化轨迹如图7、图8所示。

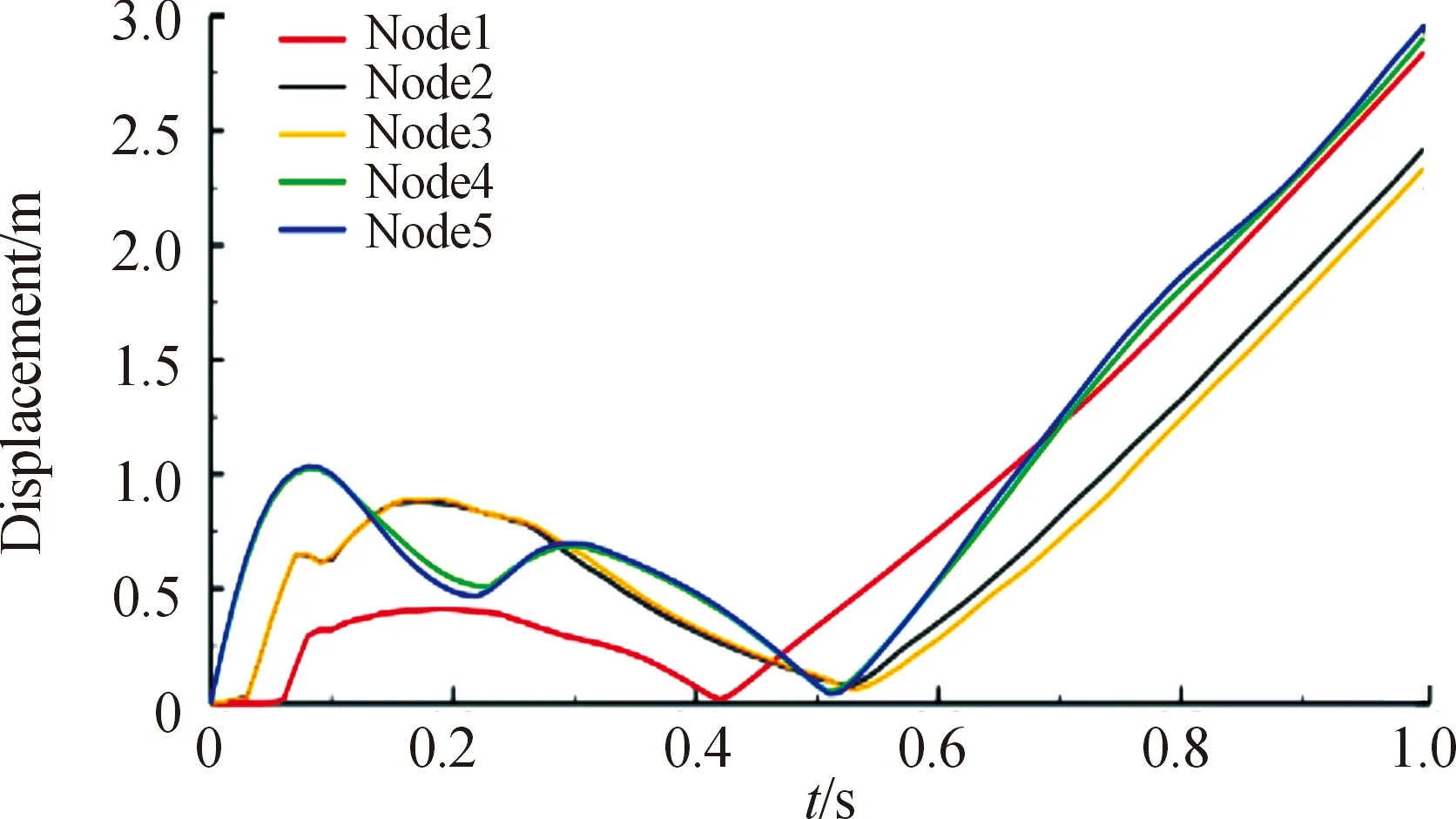
图7 柔性网动态展开过程位移-时间曲线

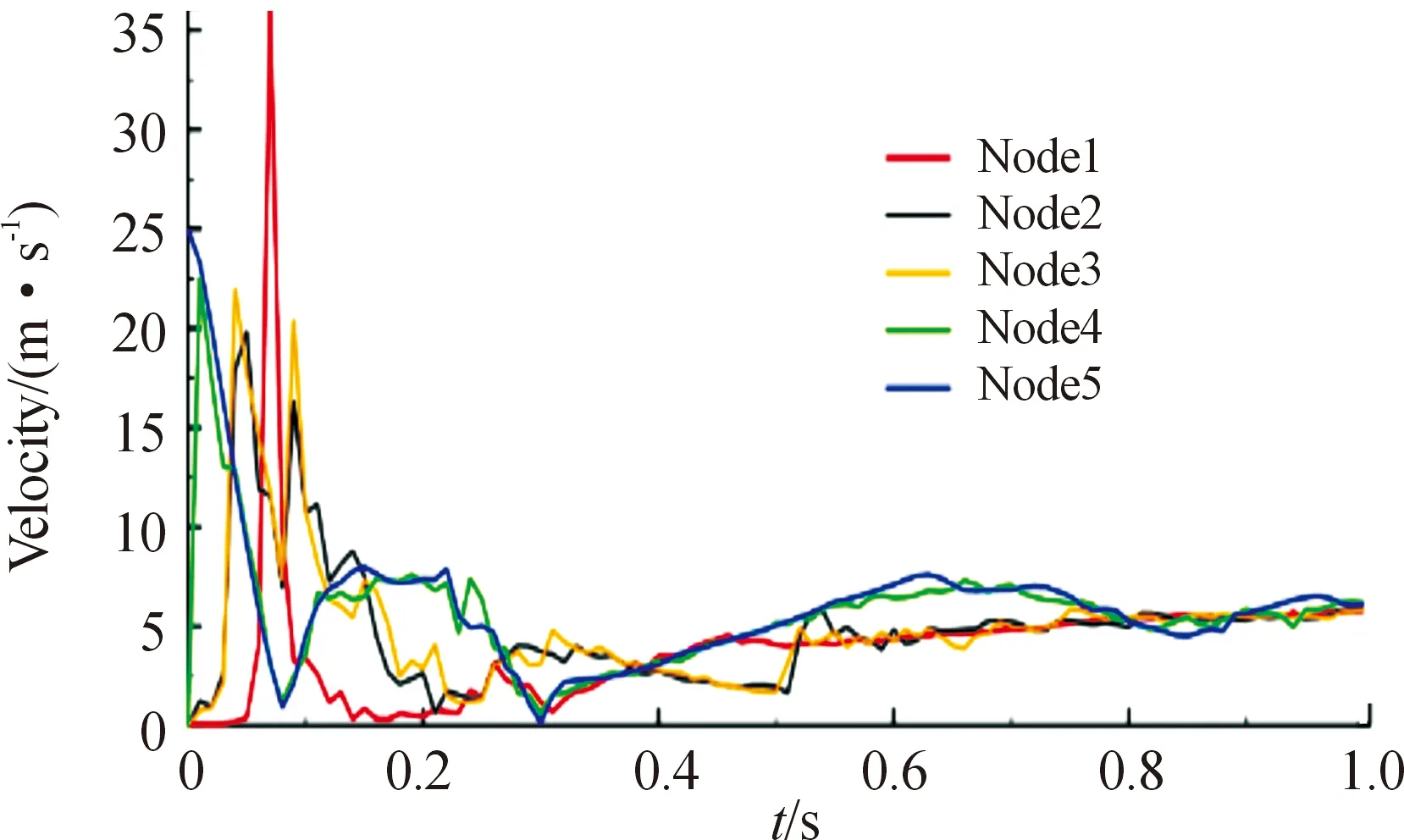
图8 柔性网动态展开过程速度-时间曲线

由图7位移轨迹曲线可知：网角节点和牵引体的位移变化轨迹大致相同、上弦节点与右弦节点的轨迹变化由于对称也几乎一致，这与直观预期想象相符。一开始随着网被逐渐拉伸展开，由于柔性网的材料非线性，各个节点位移轨迹随时间呈抛物线变化增长，而后网收缩反弹甩动并对无人机进行缠绕，故轨迹呈抛物线波动变化，最终对目标完成包裹捕获后网捕系统在重力的作用下自由下落，故轨迹呈自由落体趋势变化增长；此外在初始状态网未完全展开时，弦中节点和网中节点的位移出现一段时间保持为零的“死区”，即相对角节点和牵引体变化趋势有一定滞后，且网中节点的死区时间比弦中节点要长。

由图8速度变化轨迹可知：网拉伸展开过程，牵引体由初始发射速度25 m/s递减接近于零，而后反弹甩动缠绕而振荡变化，网中各观察节点则由于材料非线性速度随时间呈振荡变化，最终捕获目标后整体自由下落，故各节点速度随时间逐渐趋于一致。

保持其他仿真参数及设置不变，将牵引体的发射角度θ分别调整为30°、60°，得到网捕系统动态展开与捕捉过程如图9、图10所示，与图5对比分析可得，随着牵引体发射角度增加，折叠柔性网的展开速度加快，完全展开时间缩短；45°发射时网口收缩对目标形成有效包括缠绕的时间比30°发射时快0.1 s且收口效果更好；60°的展网速度虽然比45°略快，但是对目标形成有效缠绕的收口效果不如45°。图11、图12分别为不同发射角度下展网飞行捕获距离和展网投影面积随时间的变化曲线，对比分析可知：随发射角度增大，虽然展网速度略有加快，但45°下的展网最大飞行距离比30°和60°大，且45°下保持较大展网投影面积(柔性网平铺展开面积的60%以上)的相对时间更长，即45°发射角度下柔性网展开与捕获目标的时间容错性与空间容错性更大，故牵引体发射角度对柔性网的展开速度、捕获目标性能与容错能力有一定影响，在一定范围存在最优解。

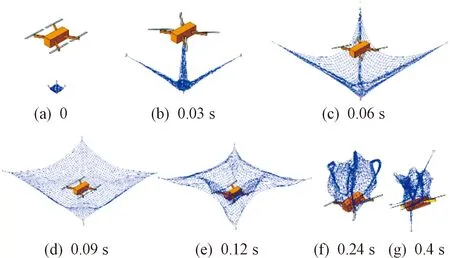
图9 网捕无人机动态过程仿真等轴测图(θ=30°)

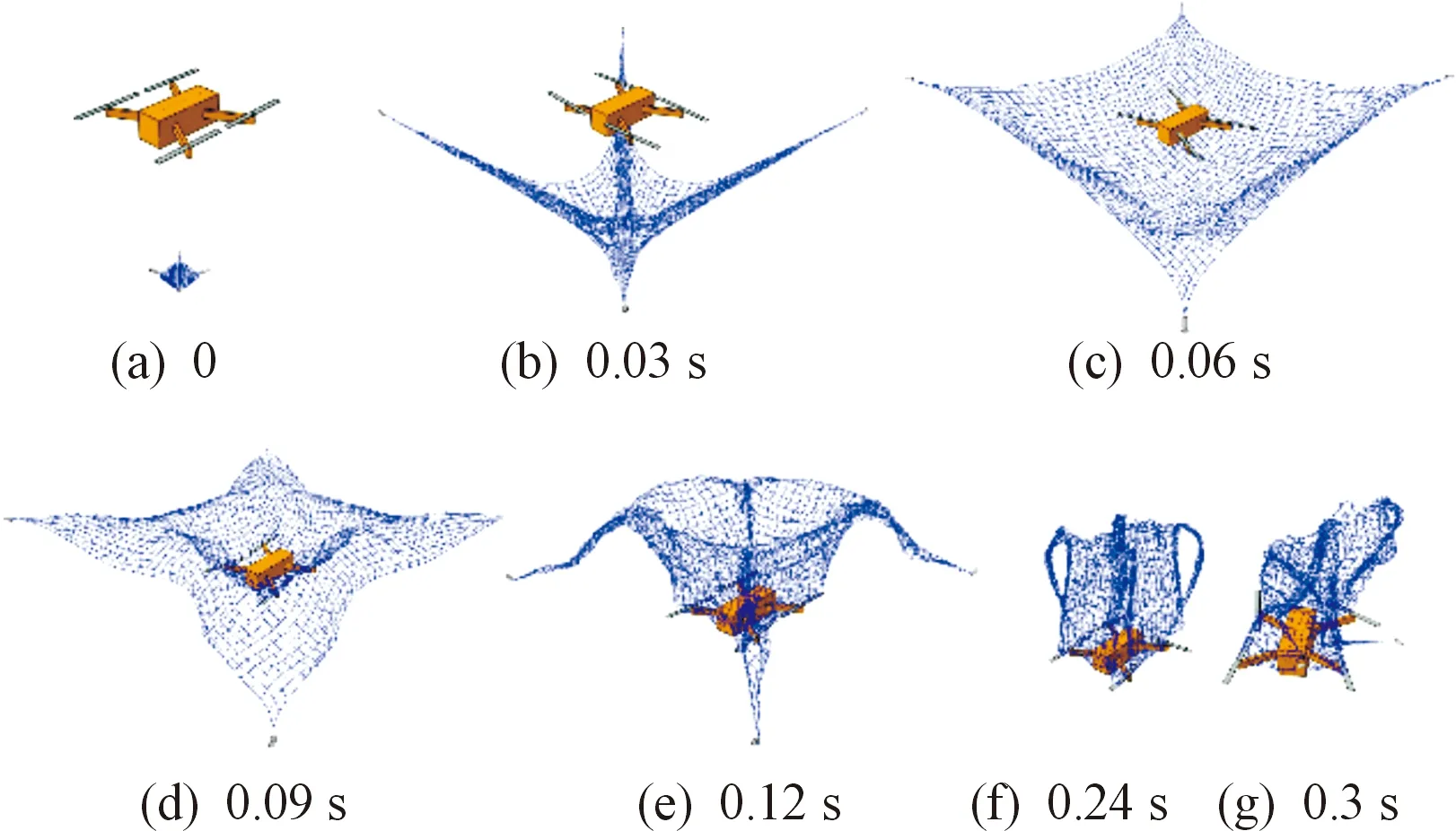
图10 网捕无人机动态过程仿真侧视图(θ=60°)Fig.10 Simulation of the dynamic process of the netting UAV (θ=60°)

图11 不同发射角度下展网飞行距离-时间曲线

4 结论

本文应用ABAQUS建立网捕无人机系统的有限元模型，对柔性网的发射动态展开与捕捉目标的动力学性能进行了初步研究，对仿真结果分析表明：

1) ABAQUS的Truss单元能够有效模拟网绳这类高柔性材料的非线性特性，可以为柔性网捕类系统的有限元建模与动力学仿真分析提供参考。

2) 柔性网完全展开与目标发生接触碰撞后，网绳之间的张力会拉动牵引体反弹收缩甩动，成功对目标形成有效缠绕包裹，实现对目标的可靠捕获。

3) 牵引体发射角度θ对折叠柔性网的动态展开速度、捕获目标性能、容错能力有较大影响，在一定范围存在最优解。