外置磁流变阻尼器高强筋材混凝土剪力墙抗震性能研究*

郭晓婧，赵 军，张香成，罗 京

(1 郑州大学土木工程学院，郑州 450001；2 郑州大学力学与安全工程学院，郑州 450001)

0 引言

作为可恢复功能混凝土结构的一种，自复位混凝土剪力墙具有良好的震后恢复能力[1]。文献[2-3]研究表明自复位剪力墙的震后残余变形较小，易于修复，但也存在着侧向位移过大、耗能能力低的缺点。

为提升可恢复结构的耗能能力，常用的做法是在结构中附加耗能元件。Kurama等[4]提出在结构上附加黏滞阻尼器来提高结构的非弹性耗能性能，主要通过裂缝张开时阻尼器的变形来消耗地震能量；Marriott等[5]研究发现安装外置耗能装置的预应力自复位剪力墙具有良好的耗能及自复位能力，耗能主要集中在外置的耗能装置上；Resrtepo和Rahman[6]在自复位剪力墙的墙体和基础之间增加了一种软钢钢筋型阻尼器，详细研究了该阻尼器对剪力墙耗能能力的影响；郭彤等[7]在自复位剪力墙与相邻重力柱连接处增设可拆卸摩擦消能器，并验证了其具有良好的抗震性能；马昕、吕西林[8]利用有限元软件建立自复位剪力墙的模型，并在墙底与基础交界处布置软钢阻尼器，分析了阻尼器数量、长度、位置等参数对结构抗震性能的影响；郑杰等[9]通过对设置金属阻尼器的缩尺竖缝剪力墙进行拟静力研究，发现该剪力墙的承载能力虽然较现浇混凝土剪力墙有所降低，但却有较好的变形和延性性能；黄信等[10]将连梁阻尼器置于剪力墙中，发现地震作用下连梁阻尼器能为结构提供附加阻尼并发挥耗能作用，且将阻尼器布置在结构中上部较为经济。

上述阻尼器属于位移型阻尼器，结构简单、方便实用，但在耗能时会产生塑性变形，不利于结构残余变形的恢复。而磁流变阻尼器(MRD)能耗低、阻尼力连续可调、响应快，是一种优秀的半主动控制装置[11]。因此，赵军等[12-14]提出了将MRD设置在自复位结构中，在不影响结构承载力和自复位能力的同时，利用MRD来增加结构的耗能能力，实现低残余变形和高耗能能力的目标。在此基础上，研究了MRD以及外置MRD高强筋材混凝土剪力墙和柱的力学性能。

为了深入开展MRD对剪力墙抗震性能影响规律的研究，本文采用ABAQUS软件建立外置MRD高强筋材混凝土剪力墙的有限元模型，对模型的滞回性能和破坏形态进行数值仿真分析，通过将有限元模型计算结果和试验结果进行对比，验证模型的有效性；然后，改变模型中MRD的阻尼力和位置，研究构件的滞回曲线、骨架曲线、耗能等抗震性能随MRD阻尼力和位置的变化规律。

1 外置MRD高强筋材混凝土剪力墙设计

共设计2个外置MRD的高强筋材混凝土剪力墙，其中1个为外置MRD的碳纤维复合材料(CFRP)筋混凝土剪力墙，编号为CFRPSW+MRD；另外1个为外置MRD的钢绞线混凝土剪力墙，编号为SSW+MRD，试件均由底梁、墙肢和加载梁三部分组成，墙肢高度(底梁上表面至加载梁中心线的距离)为2 360mm，截面尺寸为1 280mm×200mm。CFRPSW+MRD的边缘构件的纵向配筋为8根直径为12mm的CFRP筋和4根直径为8mm的HRB400级钢筋；SSW+MRD的边缘构件的纵向配筋是等配筋率的6根公称直径为15.2mm的钢绞线和4根直径为8mm的HRB400级钢筋。边缘构件中箍筋均采用直径为6mm的HRB400级钢筋，且采用矩形复合箍筋形式。墙体内所有分布钢筋均采用HRB400级钢筋。竖向分布钢筋和水平分布钢筋在距离底梁顶部600mm高度以上的配筋率均为0.7%，且竖向分布钢筋的间距为60mm，水平分布筋在距离底梁顶部600mm高度内的间距为50mm，在距离底梁顶部600mm高度以上的间距为70mm。试件尺寸及配筋见图1。

图1 试件的尺寸及配筋图

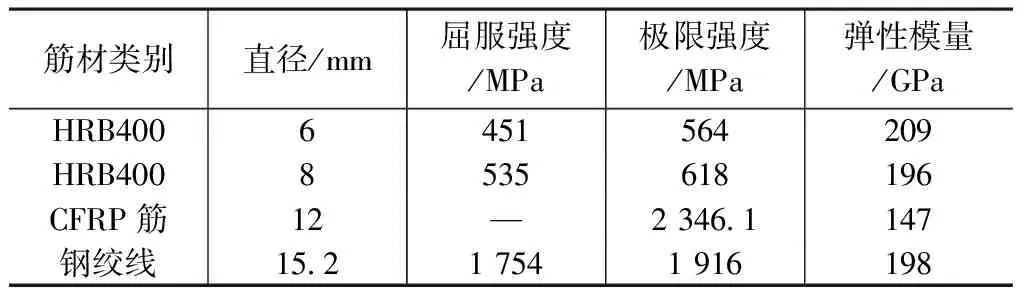
筋材的基本力学性能 表1

剪力墙外置的MRD的构造尺寸、拟静力作用下的力学性能等见文献[13]，MRD水平安装在墙体左右两侧距底梁上表面1 150mm处的中心位置，每个试件安装2个MRD。

2 数值建模

2.1 混凝土材料模型

混凝土本构模型采用ABAQUS中的损伤塑性模型(CDP模型)，模型的拉压应力-应变关系按《混凝土结构设计规范》(GB 50010—2010)[15]附录C.2中采用。CDP模型的拉压应力-应变数据在ABAQUS中以非弹性应力-应变的形式输入，ABAQUS通过式(1)将非弹性应变转化为塑性应变进行计算，轴心抗压强度按试验实测值选取。混凝土损伤因子按能量法[15]计算得到，ABAQUS中以非弹性应变-损伤因子的形式输入，拉压刚度恢复系数分别设为wt=0和wc=0.8。采用ABAQUS混凝土损伤塑性模型时，还需定义混凝土CDP模型的5个输入参数，见表2。

(1)

CDP模型输入参数 表2

2.2 筋材材料模型

在ABAQUS软件中普通钢筋、CFRP筋以及钢绞线采用了钢筋的滞回本构模型，该模型通过重加载刚度更“弱化”的钢筋本构关系和增加“滞回能耗影响系数”来描述混凝土与钢筋之间的粘结滑移损伤，是一种有效的数值分析手段[16]，具体模型见图2，图中各符号含义见文献[16]。在ABAQUS软件中每种材料需输入Es(初始刚度)、fy(屈服强度)、Esh/Es(硬化刚度与初始刚度的比值)，CFRP筋的应力-应变关系为线弹性，因此在输入时fy取其极限强度，Esh/Es取1。不同筋材的弹性模量及屈服强度采用表1的材性试验结果值。

图2 钢筋滞回模型

2.3 有限元建模

有限元建模过程中，底梁、墙体和顶梁采用整体建模的方式，可以提高整体计算效率，钢筋骨架嵌入到整个混凝土模型中，不考虑筋材与混凝土之间的粘结滑移。建模时，混凝土采用三维实体单元C3D8R，钢筋、CFRP筋以及钢绞线均采用三维桁架单元T3D2。网格划分通过布置种子来控制网格划分密度，软件自动生成相应尺寸的网格单元。生成网格后，在模型底梁底面的所有节点上施加三向位移约束，剪力墙的有限元模型如图3所示。

图3 剪力墙有限元模型

2.4 加载制度及加载方式

为尽可能做到数值模拟加载方式与前期开展的试验加载方式相吻合[12-13]，在模型加载梁顶端施加8.68N/mm2的恒定竖向均布荷载，并在模型加载梁侧面的节点上施加水平位移荷载，水平位移由图4中剪力墙的位移角乘以墙肢高度计算得到，同时在MRD安装位置的模型节点上施加28kN的水平荷载，水平荷载的方向始终与位移加载的方向相反。上述三种荷载均同步施加层间位移角对应的位移值见表3。

6月14日，全球高新技术工程和工业领域的重要领军者法国登莱秀集团（Groupe Delachaux）宣布已经于5月29日在武汉成立了新的工厂，以满足亚洲市场不断增长的需求和实现公司在亚太地区扩张的目标。截止2017年年末，亚太地区的销售额已经占其总销售额的29%。登莱秀集团武汉工厂占地面积14 000 m2，雇佣人数超过200人。该工厂生产登莱秀集团在铁路基础设施以及能源和数据管理系统设施领域的全系列产品，是登莱秀集团全球唯一在同一厂房内生产这两种类型产品的工厂。该工厂是登莱秀集团在亚洲的旗舰，充分体现了集团的技术实力，以及在管理、环境和安全方面的最佳实践。

图4 剪力墙和MRD的加载制度

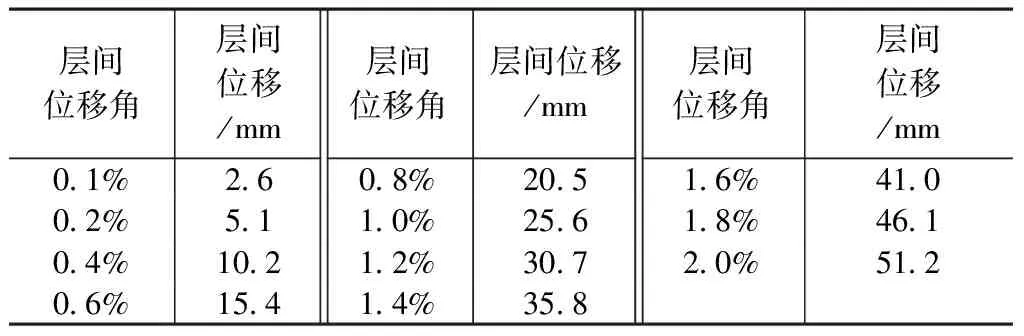
层间位移角对应的位移值 表3

3 数值模型计算结果及验证

为验证本文有限元模型的有效性，将模型计算结果与试验结果进行对比分析。

3.1 滞回性能对比分析

试件CFRPSW+MRD与试件SSW+MRD有限元模拟结果与试验结果对比如图5所示，各加载位移下水平荷载试验值与有限元模拟值见表4。从图5可以看出，在加载前期，试验和有限元模拟的骨架曲线均近似为直线，随着层间位移的增大，骨架曲线均表现出非线性的特征，在达到较大层间位移时仍具有较高的承载力，对于试件CFRPSW+MRD，由图5和表4可知，试验在层间位移为30.7mm时正向和负向峰值荷载分别为967.28，-993.38kN，而有限元模拟在层间位移为46.1mm时达到正向峰值荷载962.70kN，层间位移为41.0mm时达到负向峰值荷载-972.61kN，两者的峰值荷载比较接近。对于试件SSW+MRD，试验在层间位移为46.1mm时达到正向峰值荷载1 030.57kN，层间位移为41.0mm时达到负向峰值荷载-1 139.01kN，而有限元模拟在层间位移为46.1mm时正向和负向峰值荷载分别为1 118.21，-1 046.76kN。试件CFRPSW+MRD和试件SSW+MRD达到的峰值荷载吻合度较高。可以看出，各加载等级下的水平荷载与拟静力试验得到的数值误差较小，两者骨架曲线基本吻合。

图5 滞回曲线对比

3.2 破坏形态对比分析

试件CFRPSW+MRD与试件SSW+MRD有限元模拟受压损伤结果与试验结果对比分别见图6，7。

图6 试件CFRPSW+MRD受压损伤云图

由于采用了混凝土塑性损伤模型，在计算结果中可以通过查看混凝土的受压损伤因子的变化和分布情况对墙体的破坏特征进行判断。首先，墙体底部两侧混凝土出现损伤，随着水平位移逐渐增大，损伤位置逐渐上移，之后墙底角部混凝土损伤逐渐加剧，并沿斜向45°方向逐渐上升发展，和试验中发生的边缘根部压溃及墙体底部局部混凝土外鼓剥离的现象吻合良好。

以上分析结果表明：ABAQUS软件的模拟分析结果与试验结果基本吻合，说明所采用的有限元模型能够较准确地模拟试验，可用于参数分析。

各加载位移下水平荷载试验值与有限元模拟值对比 表4

图7 试件SSW+MRD受压损伤云图

4 参数分析

在第2节已建模型的基础上，改变模型中MRD阻尼力大小和位置，研究二者对剪力墙抗震性能的影响规律。MRD阻尼力的大小分别为28，84，140kN，距底梁顶面的水平安装高度分别为450，1150，1 900mm。

4.1 试件CFRPSW+MRD的抗震性能

4.1.1 滞回曲线

不同MRD阻尼力和位置工况下，试件CFRPSW+MRD的滞回曲线见图8。由图8可知，总体来看，在加载初期，试件CFRPSW+MRD的侧向变形均较小，初期刚度较大，滞回曲线近似为直线，墙体基本处于弹性状态；随着荷载增加，刚度逐渐表现出退化的趋势，滞回环的面积增大，耗能能力增大的同时也产生残余变形，在层间位移为41，46.1mm时达到峰值荷载然后开始下降至破坏。此外，随着MRD阻尼力的增大，滞回环逐渐饱满，滞回环面积增大，表明试件的耗能能力以及承载能力均增加；随着MRD安装高度的增加，MRD对试件耗能能力和承载能力的影响越来越明显，特别是安装高度较高时耗能随阻尼力增大的现象更明显。这是因为当MRD安装高度越高时，同级荷载作用下水平荷载随阻尼力的提升越明显所致。

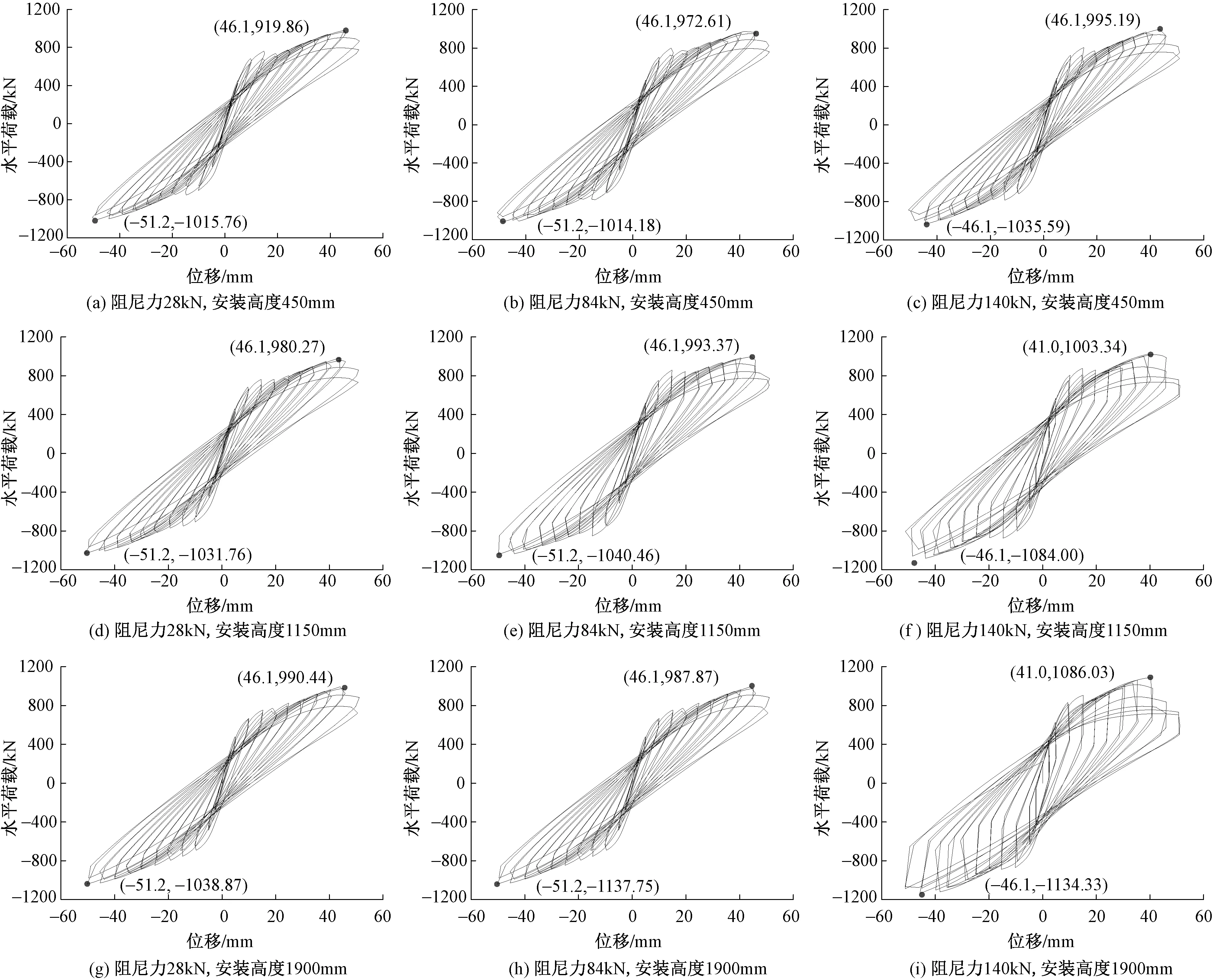
图8 试件CFRPSW+MRD的滞回曲线随MRD阻尼力和安装高度的变化规律

4.1.2 骨架曲线

图9给出了试件CFRPSW+MRD的骨架曲线随MRD阻尼力和安装高度的变化规律。由图9可知，当MRD安装高度为450mm时，MRD阻尼力对试件骨架曲线的影响非常小，三条曲线几乎重合。当层间位移为46.1mm时，与阻尼力28，84，140kN对应的骨架曲线侧向荷载分别为979.86，980.27，990.44kN，最大相差1.08%；随着MRD安装高度的增加，MRD的阻尼力对试件侧向荷载的影响越来越明显，当MRD安装高度为1 900mm，层间位移为41.0mm时，与阻尼力28，84，140kN对应的骨架曲线侧向荷载分别为951.32，996.78，1 086.03kN，最大相差14.16%。当MRD阻尼力恒定时，试件的峰值荷载随MRD安装高度的增加而略微增大。当阻尼力为84kN，层间位移为46.1mm时，与MRD安装高度450，1 150，1 900mm对应的骨架曲线侧向荷载分别为980.27，993.78，1 003.34kN，最大相差2.35%。此外，随着阻尼力的增加，试件的侧向刚度不断增大，并且在MRD安装高度较大时这种现象更加明显。

图9 试件CFRPSW+MRD的骨架曲线随MRD阻尼力和安装高度的变化规律

4.1.3 耗能曲线

通过计算各滞回环的面积，得到剪力墙试件的累积耗能及总耗能，如图10和表5所示。图10给出了试件CFRPSW+MRD的累积耗能随MRD阻尼力和安装高度的变化规律。由图10可知，当MRD安装高度为450mm时，MRD阻尼力对试件累积耗能的影响非常小，三条曲线几乎重合。当层间位移角为2%时，与阻尼力28，84，140kN对应的累积耗能分别为294.33，321.54，349.16kN·m，最大相差18.63%；随着MRD安装高度的增加，MRD的阻尼力对试件累积耗能的影响越来越明显，当MRD安装高度为1 900mm，层间位移角为2%时，与阻尼力28，84，140kN对应的累积耗能分别为364.44，549.33，710.51kN·m，最大相差94.96%。当MRD阻尼力大小恒定时，试件的累积耗能随MRD安装高度的增加而明显增大，当阻尼力为84kN，层间位移角为1.6%时，与MRD安装高度450，1 150，1 900mm对应的累积耗能分别为192.15，278.22，357.46kN·m，最大相差86.03%。

图10 试件CFRPSW+MRD的累积耗能随MRD阻尼力和安装高度的变化规律

综合以上分析，对于试件CFRPSW+MRD，当阻尼器设在距底梁顶面1 900mm位置且阻尼力为84kN时，无论承载力还是耗能能力，都表现良好。

MRD不同高度、不同阻尼力时试件CFRPSW+MRD模型的总耗能对比/(kN·m) 表5

4.2 试件SSW+MRD的抗震性能

4.2.1 滞回曲线

不同MRD阻尼力和位置工况下，试件SSW+MRD的滞回曲线见图11。由图11可知，试件SSW+MRD在加载前期的滞回性能与试件CFRPSW+MRD基本一致，随着加载等级的提高，滞回环的面积增大，耗能能力逐渐提高。当MRD安装在距基础梁顶面450mm位置处时，试件滞回曲线均呈细长的弓形，无明显的下降段，破坏荷载即为峰值荷载。随着MRD安装高度的增加，滞回环的面积明显增大，且在层间位移为46.1mm时达到峰值荷载，然后开始下降至破坏。此外，随着MRD阻尼力的增大，MRD对试件耗能能力和承载能力的影响越来越明显，且在安装高度较高时耗能随阻尼力增大的现象更加明显。

图11 试件SSW+MRD的滞回曲线随MRD阻尼力和安装高度的变化规律

4.2.2 骨架曲线

图12给出了试件SSW+MRD的骨架曲线随MRD阻尼力和安装高度的变化规律。由图12可知，当MRD安装高度为450mm时，MRD阻尼力对试件骨架曲线的影响非常小，三条曲线几乎重合。当层间位移为46.1mm时，与阻尼力28，84，140kN对应的骨架曲线水平荷载分别为1 043.39，1 035.52，1 039.62kN，最大相差0.75%；随着MRD安装高度的增加，MRD的阻尼力对试件水平荷载的影响越来越明显。当MRD安装高度为1 900mm，层间位移为46.1mm时，与阻尼力28，84，140kN对应的骨架曲线水平荷载分别为1 034.689，981.12，853.06kN，最大相差21.29%。当MRD阻尼力恒定时，试件的峰值荷载随MRD安装高度的增加而略微增大，例如，当阻尼力为140kN，层间位移为35.8mm时，与MRD安装高度450，1 150，1 900mm对应的骨架曲线水平荷载分别为1 018.82，1 088.85，1 092.61kN，最大相差7.24%。

图12 试件SSW+MRD的骨架曲线随MRD阻尼力和位置高度的变化规律

此外，随着阻尼力的增加，试件的侧向刚度不断增大，并且在MRD安装高度较大时这种现象也表现得更加明显。

4.2.3 耗能曲线

通过计算各滞回环的面积，得到剪力墙试件的累积耗能及总耗能，如图13和表6所示。图13给出了试件SSW+MRD的累积耗能随MRD阻尼力和安装高度的变化规律。由图13可知，当MRD安装高度为450mm时，MRD阻尼力对试件累积耗能的影响较小，三条曲线差距不大。当层间位移角为2.0%时，与阻尼力28，84，140kN对应的累积耗能分别为304.28，380.33，355.80kN·m，最大相差24.99%；随着MRD安装高度的增加，MRD的阻尼力对试件累积耗能的影响越来越明显，当MRD安装高度为1 900mm，位移角为2.0%时，与阻尼力28，84，140kN对应的累积耗能分别为316.41，526.96，674.42kN·m，最大相差113.15%。当MRD阻尼力恒定时，试件的累积耗能随MRD安装高度的增加而明显增大，当阻尼力为84kN，层间位移角为1.8%时，与MRD安装高度450，1 150，1 900mm对应的累积耗能分别为380.33，512.09，526.96kN·m，最大相差38.55%。

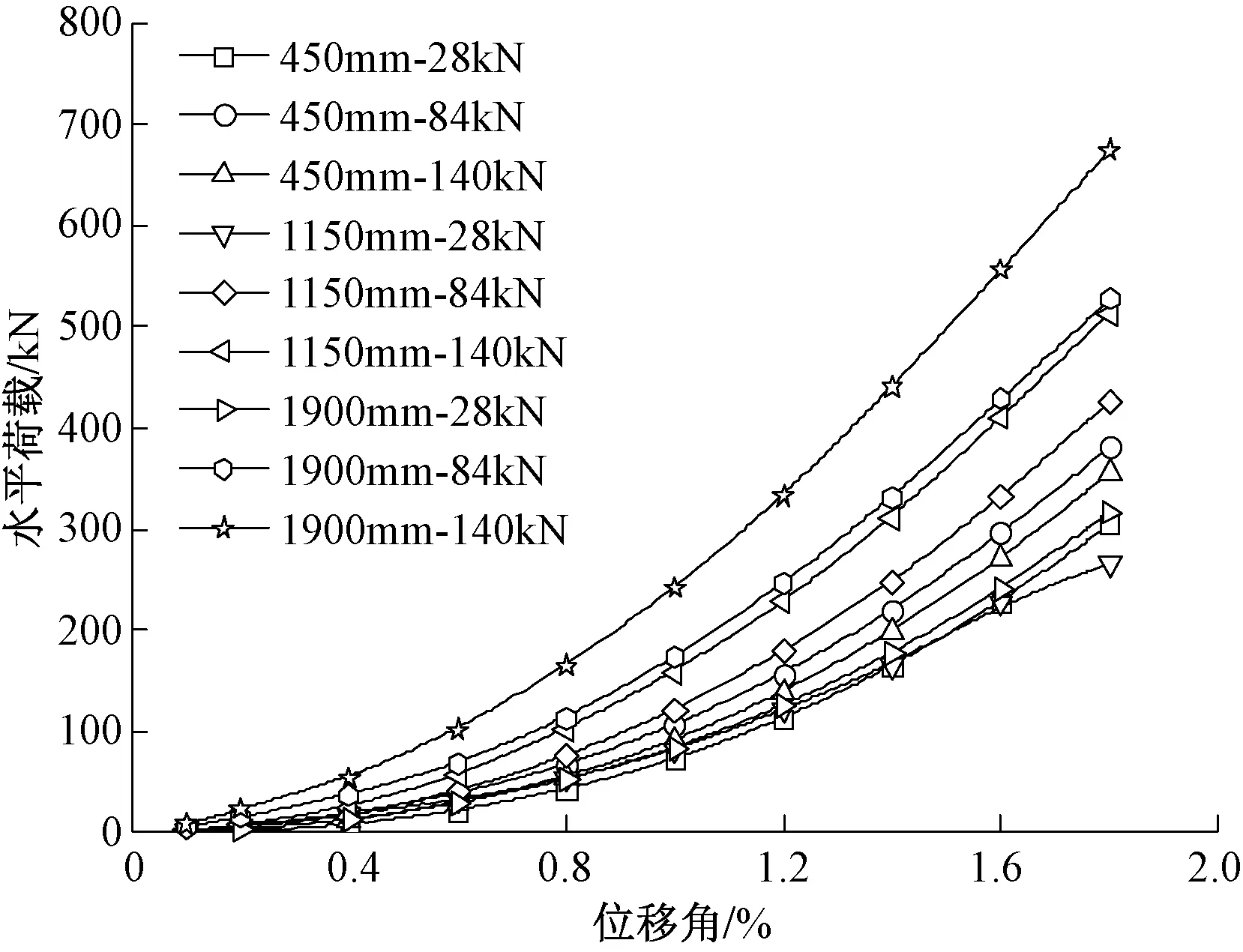
图13 试件SSW+MRD的累积耗能随MRD阻尼力和安装高度的变化规律

综合以上分析，对于试件SSW+MRD，当阻尼器设在距底梁顶面1 900mm位置且阻尼力为140kN时，无论承载力还是耗能能力，都表现良好。

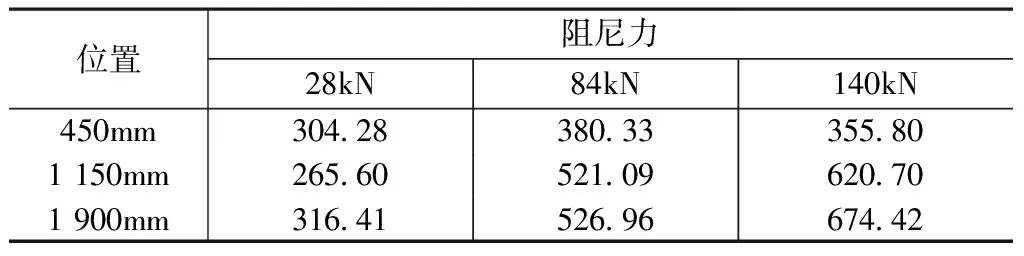
MRD不同高度、不同阻尼力时试件SSW+MRD模型的总耗能对比/(kN·m) 表6

5 结语

(1)本文建立的外置MRD高强筋材混凝土剪力墙的数值模型能有效地模拟该剪力墙的抗震性能随MRD的阻尼力和安装高度的变化规律。

(2)CFRP筋和钢绞线的高抗拉强度保证了剪力墙在较大变形下仍具有较高的承载能力，且两个剪力墙在加载结束后的耗能较大，体现出了良好的滞回性能。

(3)在高强筋材混凝土剪力墙外部安装MRD能增加其承载能力和耗能能力。随着MRD阻尼力的增大，试件的耗能能力、承载能力均增加；随着MRD安装高度的增加，MRD对试件耗能能力和承载能力的影响越来越明显。