一道2020年高考数列题的十种证法探究

武增明

(云南省玉溪第一中学 653100)

试题设数列{an}满足a1=3，an+1=3an-4n.

(1)计算a2，a3，猜想{an}的通项公式并加以证明；

(2)求数列{2nan}的前n项和Sn.

这是2020年高考全国Ⅲ卷理科数学第17题.

这道考题的第(1)问是以数列递推式为背景，求数列的通项公式问题，此问题符号优美，题面简洁，构思巧妙，立意新颖，让人赏心悦目，耐人寻味，回味无穷，涉及的数学知识和蕴含的数学思想方法非常丰富，逻辑推理性很强，具有很大的探究价值，具有很高的训练价值，具有很强的代表性，是一道训练数学思维的好题，很值得深入探究.于是，引起笔者极大的探究兴趣与热情.下面给出此题第(1)问的十种证法，旨在供同仁在教学过程中作参考，旨在对同学们在学习这类问题时有所帮助和启示.

证法1 (试验法)a2=5，a3=7.猜想an=2n+1，证明如下：

若an=2n+1，则an+1=2(n+1)+1=2n+3，

又3an-4n=3(2n+1)-4n=6n+3-4n=2n+3，

此时an+1=3an-4n成立，所以an=2n+1.

证法2 (数学归纳法)a2=5，a3=7.猜想an=2n+1，证明如下：

(1)当n=1时，由an=2n+1知，a1=3，符合题意，故当n=1时，an=2n+1成立.

(2)假设当n=k(k∈N*)时，an=2n+1成立，即ak=2k+1成立.

则n=k+1时，因为ak+1=3ak-4k=3(2k+1)-4k=2(k+1)+1，

所以当n=k+1时，an=2n+1成立.

由(1)，(2)可知，对于任意正整数n，an=2n+1成立.

证法3(正向思维迭代递推法)a2=5，a3=7.猜想an=2n+1，证明如下：

因为an+1=3an-4n，

所以a2-5=3(a1-3)，

a3-7=3(a2-5)，

a4-9=3(a3-7)，

……

an-(2n+1)=3[an-1-(2n-1)].

因为a1-3=0，

所以an-(2n+1)=0，即an=2n+1.

证法4(逆向思维迭代递推法)a2=5，a3=7.猜想an=2n+1，证明如下：

由已知可得an+1-(2n+3)=3[an-(2n+1)]，

an-(2n+1)=3[an-1-(2n-1)]，

……

a2-5=3(a1-3).

因为a1=3，即a1-3=0，

所以an-(2n+1)=0，即an=2n+1.

证法5(逆向思维迭代递推法)a2=5，a3=7.猜想an=2n+1，证明如下：

因为an+1=3an-4n，①

所以an=3an-1-4(n-1)，②

①-②，得an+1-an=3an-3an-1-4，

所以an+1-an-2=3(an-an-1-2)，

所以an-an-1-2=3(an-1-an-2-2)，

……

a4-a3-2=3(a3-a2-2)，

a3-a2-2=3(a2-a1-2).

因为a2-a1-2=0，所以an+1-an-2=0.

于是数列{an}是首项为a1=3，公差d=2的等差数列，故an=a1+(n-1)d，从而an=3+(n-1)·2，即an=2n+1.

证法6(逆向思维迭代递推法)a2=5，a3=7.猜想an=2n+1，证明如下：

因为an+1=3an-4n

①

所以an=3an-1-4(n-1)

②

①-②，得an+1-an=3an-3an-1-4，

所以an+1-an-2=3(an-an-1-2)，

所以an+1-an-2=3(an-an-1-2)=32(an-1-an-2-2)=33(an-2-an-3-2)=…=3n-1(a3-a2-2)=3n(a2-a1-2).

因为a2-a1-2=0，所以an+1-an-2=0.

于是数列{an}是首项为a1=3，公差d=2的等差数列，故an=a1+(n-1)d，从而an=3+(n-1)·2，即an=2n+1.

证法7 (逆向思维迭代递推法)a2=5，a3=7.猜想an=2n+1，证明如下：

令bn=an-(2n+1)，因为an+1=3an-4n，所以bn+1=3bn，从而bn+1=3bn=32bn-1=33bn-2=…=3n-1b2=3nb1.

所以b1=0，故bn=0，即an-(2n+1)=0，于是an=2n+1.

证法8(逆向思维待定系数法)a2=5，a3=7.猜想an=2n+1，证明如下：

设an+1+k(n+1)+b=3an+(k-4)n+k+b，则

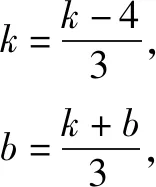
从而an+1-2(n+1)-1=3(an-2n-1)，

所以an-2[(n-1)+1]-1=3[an-1-2(n-1)-1]

……

a4-2(3+1)-1=3(a3-2×3-1)，

a3-2(2+1)-1=3(a2-2×2-1)，

a2-2(1+1)-1=3(a1-2×1-1)，

因为a1-2×1-1=0，所以an-2n-1=0，即an=2n+1.

证法9 (待定系数法)a2=5，a3=7.猜想an=2n+1，证明如下：

将an+1=3an-4n两边同除3n+1，得

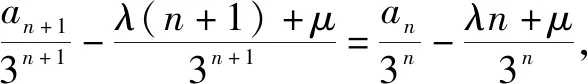
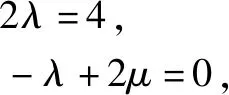
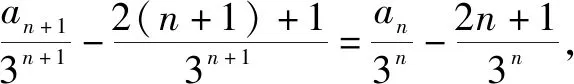
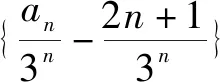
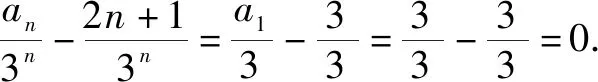
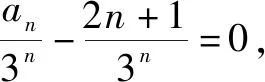
证法10 (迭加法)a2=5，a3=7.猜想an=2n+1，证明如下：

将an+1=3an-4n两边同除3n+1，得

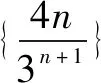
①

②

①-②，得

……

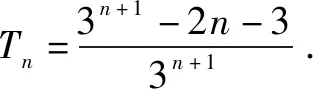
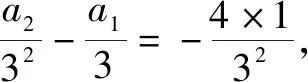
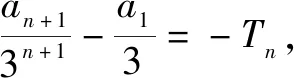
从而an=2n+1.

作为学生领路人的教师，一些前因后果需要我们教者从其背后去思考、挖掘，只有潜心研究高考试题，从中探究出更多潜在价值，才能在高中数学教学中高屋建瓴、有的放矢，才能确保对学生的指导方法得当、条理清楚、思路流畅.潜心研究高考试题，在寻求解法的同时，要领略考题的本质，挖掘其深刻的内涵，才能充分发挥考题的功能和作用.