一道高考压轴题引发的圆锥曲线定点问题探究

胡贵平

(甘肃省白银市第一中学 730900)

解析几何中证明直线过定点，一般是选择参数表示直线方程、数量积、比例关系等，根据等式的恒成立、数式变换，通过推理、计算，找出参数之间的关系，并消去部分参数，将直线方程化为点斜式方程，从而得到直线所过的定点.当定点具备一定的限制条件时，可先探索出定点，再证明该定点与变量无关.

一、试题呈现

(1)求C的方程；

(2)点M，N在C上，且AM⊥AN，AD⊥MN，D为垂足.证明：存在定点Q，使得|DQ|为定值.

本题综合考查直观想象、逻辑推理、数学运算等数学核心素，考查了椭圆的标准方程和性质，圆锥曲线中的定点定值问题.

二、试题解析

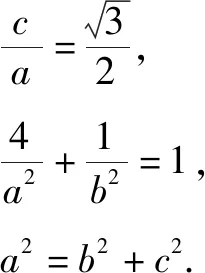
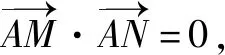
(x1-2)(x2-2)+(y1-1)(y2-1)=0

①

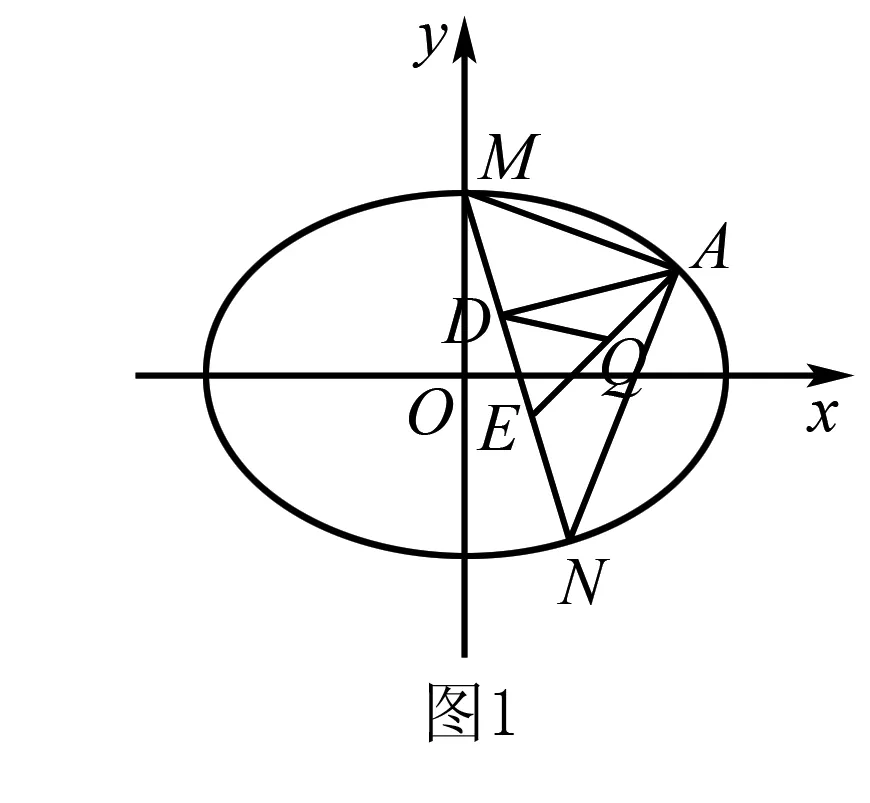
当直线MN的斜率存在时，设方程为y=kx+m,如图1.

代入椭圆方程消去y并整理,得

(1+2k2)x2+4kmx+2m2-6=0，

②

根据y1=kx1+m,y2=kx2+m,

代入①整理，可得

(k2+1)x1x2+(km-k-2)(x1+x2)+(m-1)2+4=0

将②代入，

整理化简得(2k+3m+1)(2k+m-1)=0，

因为A(2,1)不在直线MN上，所以2k+m-1≠0，

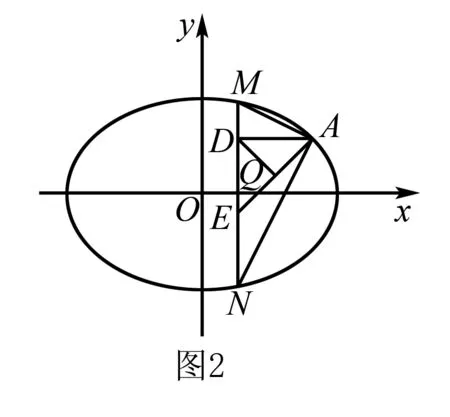
当直线MN的斜率不存在时，可得N(x1,-y1)，如图2.

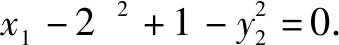
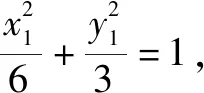
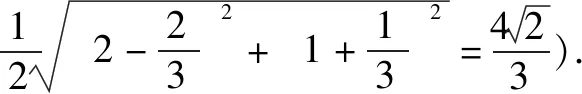
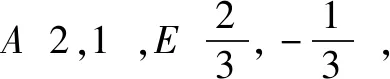
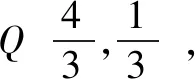
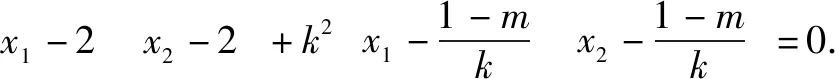
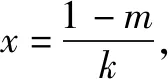
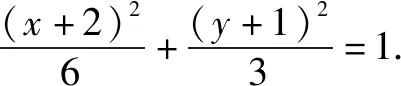
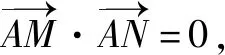
①

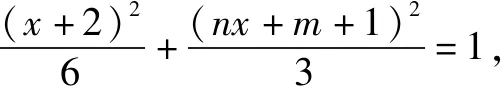
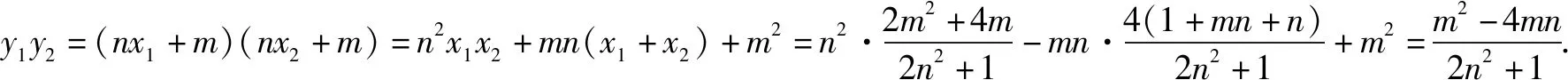
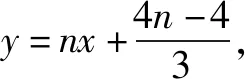
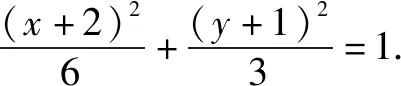
三、引申探究

对于椭圆上一点作张角为直角所对的弦是否都过定点呢？

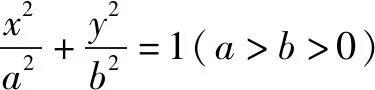
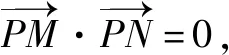
当直线MN的斜率存在时，设方程为y=kx+m,

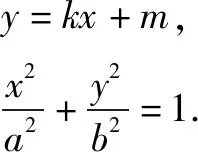
②

根据y1=kx1+m,y2=kx2+m,代入①整理，

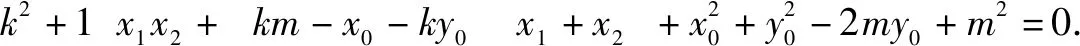
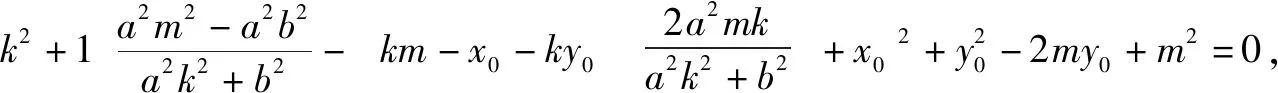
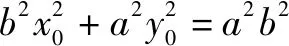
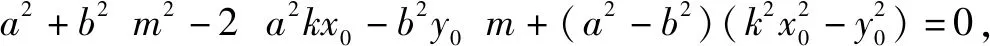
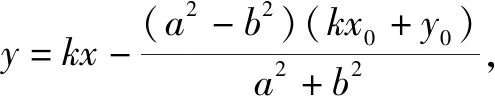
当直线MN的斜率不存在时，可得N(x1,-y1),

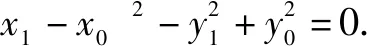
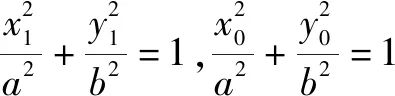
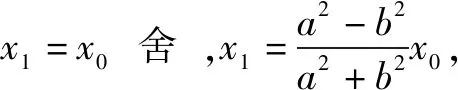
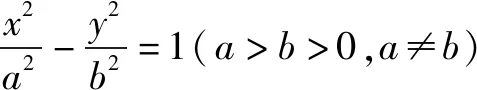
性质3 过抛物线y2=2px(p>0)上一点P(x0,y0)作两条互相垂直的弦PM，PN，则直线MN恒过定点(2p+x0,-y0).

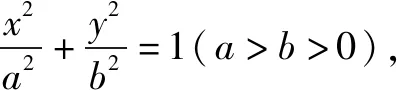
过圆锥曲线上一点P(x0,y0)作两条直线互相垂直加强到两条直线斜率之积是定值，是否仍然有张角所对的弦必过定点？

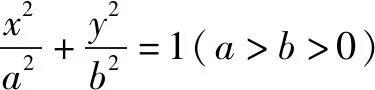
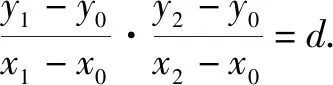
即d(x1-x0)(x2-x0)-(y1-y0)(y2-y0)=0,①

当直线MN的斜率存在时，设方程为y=kx+m,

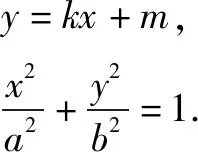
②

根据y1=kx1+m,y2=kx2+m,代入①整理，

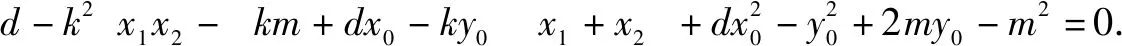
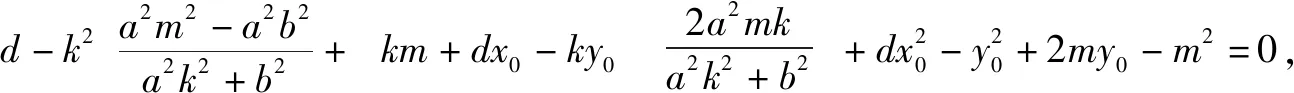
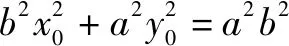
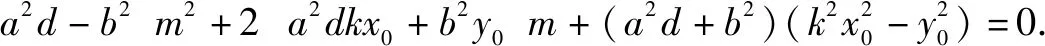
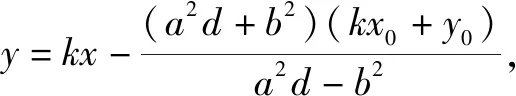
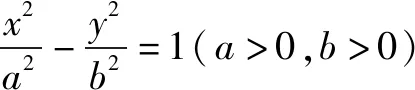
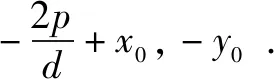
过圆锥曲线上一点P(x0,y0)作两条直线斜率之积是定值，拓展到两条直线斜率之和是定值，是否仍然有张角所对的弦必过定点？

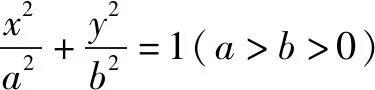
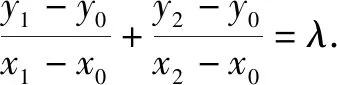
①

当直线MN的斜率存在时，设方程为y=kx+m,

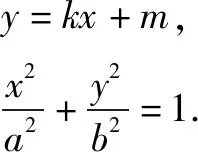
②

根据y1=kx1+m,y2=kx2+m,代入①整理，

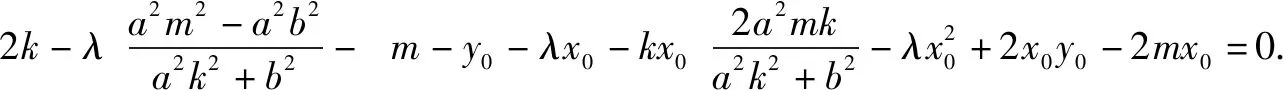
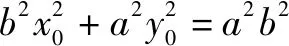
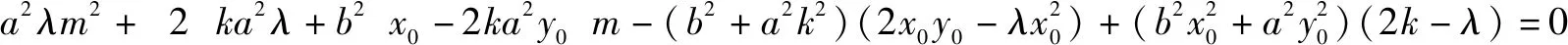
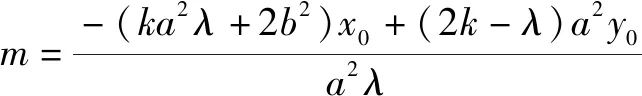
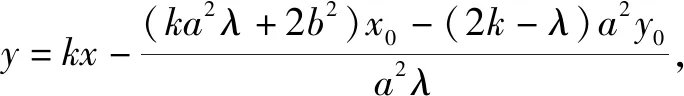
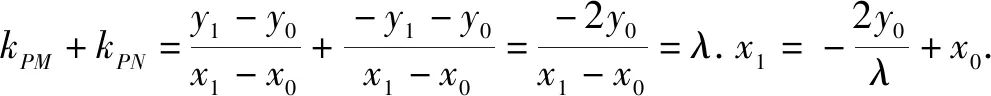
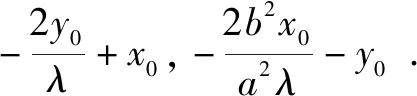
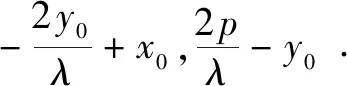
圆锥曲线上一定点P与另外两点M，N的斜率之和或斜率之积为定值时，在斜率存在时，可设MN的方程y=kx+m与圆锥曲线方程联立，根据斜率之和或斜率之积建立起参数k，m之间的关系(若是关于k，m之间是一元二次方程，要特别注意因式分解)，就可以得出直线过的定点，再在直线斜率不存在时单独验证.