高考中解三角形常考题的分类例析

范习昱

(江苏省镇江市丹徒高级中学 212143)

在高考中，相比其它知识点，对于解三角形这一内容来说，其常考题型和考查方式相对较为固定，难度也不算太大，是考生的基础得分处，其重要性不言而喻.在我的教学实践中，却总发现很多学生依然显得颇为困难，失分严重.在近十年的各地的高考试卷中，特精选了部分经典的高考题加以分类例析，从此类问题的常规解题思路出发，分析和总结了一些具有规律性的东西，希望对读者有帮助.

一、求解三角形中的角与边或其它相关要素

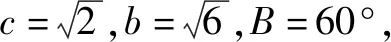
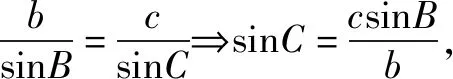
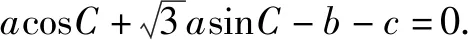
(1)求A；

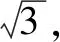
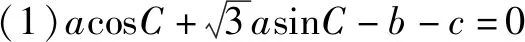
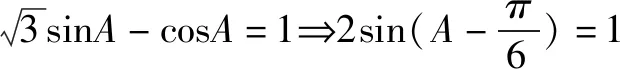
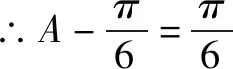
a2=b2+c2-2bccosA⟹4=b2+c2-bc,

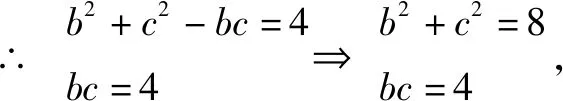
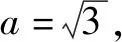
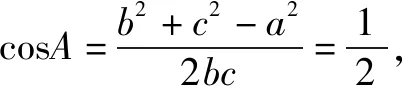
反思总结求解三角形的某个角或者边，是高考中解三角形常考题型中最为基础的一类，难度一般不大，主要考查正余弦定理的直接应用，解题的关键在与边角的合理互化，出现多解要注意检验取舍.一些高考题中还会考查三角形的外接圆的半径或者面积公式，但学生只要用对公式，有一定的转化能力还是可以顺利求解的.

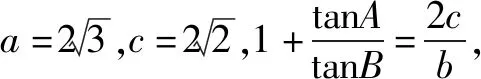
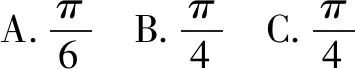
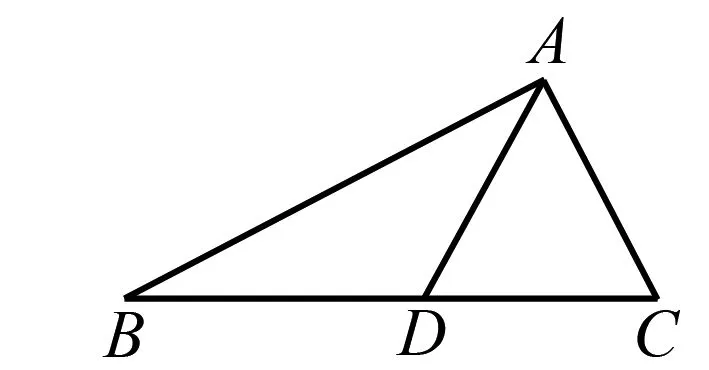
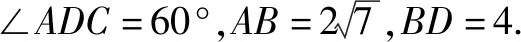
(1)求△ABD的面积.

(2)若∠BAC=120°,求AC的长.

练一练A答案：

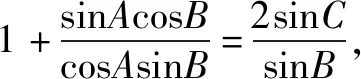
2.(1)由题意，∠BDA=120°

在△ABD中，由余弦定理可得AB2=BD2+AD2-2BD·AD·cos120°

即28=16+AD2+4AD⟹AD=2或AD=-6(舍)，

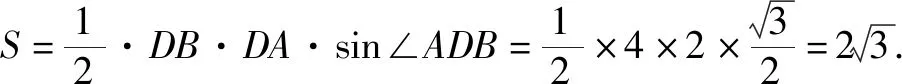
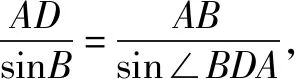
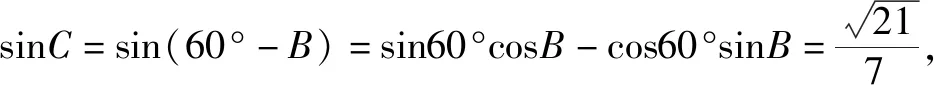
二、判断三角形的形状

例4在△ABC中，角A，B，C所对应的边分别是a,b,c，若c=2acosB,则三角形一定是( ).

A.等腰直角三角形 B.直角三角形

C.等腰三角形 D.等边三角形

解析∵c=2acosB,由正弦定理c=2RsinC,a=2RsinA,∴sinC=2sinAcosB

∵A,B,C为△ABC的内角，∴sinC=sin(A+B),A,B∈(0,π),

∴sin(A+B)=2sinAcosB,sinAcosB+cosAsinB=2sinAcosB，整理得sin(A-B)=0,

∴A-B=0,即A=B.故△ABC一定是等腰三角形.故选C.

例5 在△ABC中，角A，B，C所对的边分别为a,b,c，且b2+c2=a2+bc，若sinB·sinC=sin2A,则△ABC的形状是( ).

A.等腰三角形 B.直角三角形

C.等边三角形 D.腰直角三角形

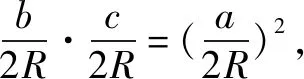
反思总结判断三角形的形状是高考中解三角形中常见的题型，频率很高，由于都是涉及三角形的核心知识并且起点低深受命题者的青睐.解题的关键是将题目的条件一般是含有边和三角函数方程统一为边或者角的形式，再进行化简就可以判断出来.值得注意的是，这类题往往会结合三角恒等变换，比如两角和与差的三角函数公式、二倍角公式等等，这对考生的三角恒等变换能力提出了很高的要求.

练一练B：1.△ABC的内角A,B,C的对边分别是a,b,c且满足acosB-bcosA=c，则△ABC是( ).

A.锐角三角形 B.直角三角形

C.钝角三角形 D.等腰三角形

A.直角三角形 B.钝角三角形

C.等腰直角三角形 D.等边三角形

练一练B答案：

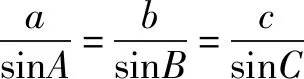
sinAcosB-sinBcosA=sinC,即sin(A-B)=sinC,

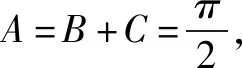
则△ABC为直角三角形，故选B.

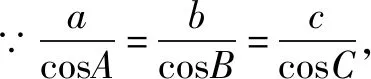
三、求解三角形中相关要素的最值或范围

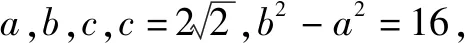
解析在△ABC中，由角C的余弦定理可知：

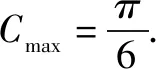
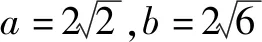
例7已知△ABC的三边a,b,c成等比数列，a,b,c所对的角分别为A,B,C，则sinB+cosB的取值范围是____.

解析∵△ABC的三边a,b,c成等比数列，

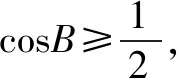
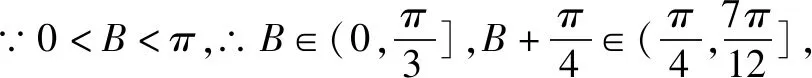
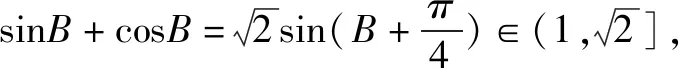
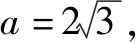
解析∵(b+2sinC)cosA=-2sinAcosC,

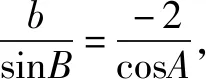
练一练C：

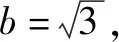
练一练C答案：

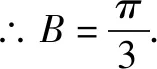
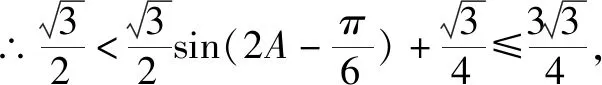
反思总结求解三角形中边、角或者面积等三角形相关要素的最值或范围是高考解三角形题型的常考题型，也是让学生感到较为困难的题型.解三角形题型的最值问题最为本质的方法是构建某个角的三角函数，再利用三角函数的图象和性质求其最值或者范围.有时也转化为边，这时可以利用基本不等式进行放缩求最值，但对于求范围来说并不理想，这也是转化为边之后处理方式的最大弊端，在学生作业中经常会出现求解范围不全的情况.弥补的方法是寻找边之间的其它不等关系，比如三角形中任意两边之和大于第三边等等一些边之间的关系，再次利用不等式的性质进行放缩求最值.

四、基于解三角形的简单综合问题

例9在△ABC中，内角A，B，C所对的边分别为a，b，c，已知m=(a,c-2b)，n=(cosC,cosA)，且m⊥n.

(1)求角A的大小；

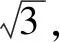
解析(1)由m⊥n，可得m·n=0，即2bcosA=acosC+ccosA，

即2sinBcosA=sinAcosC+sinCcosA，即2sinBcosA=sin(A+C)，

∵sin(A+C)=sin(π-B)=sinB，∴2sinBcosA=sinB，即sinB(2cosA-1)=0，

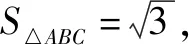
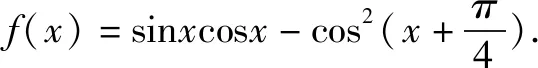
(1)求f(x)的单调区间；

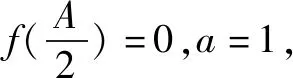
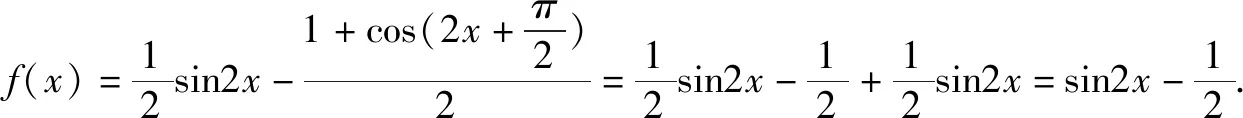
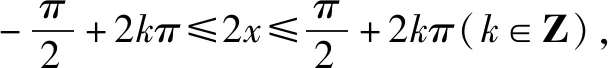
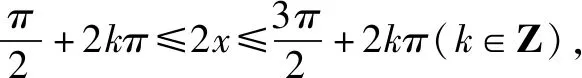
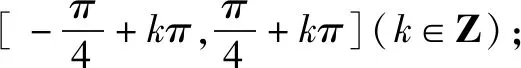
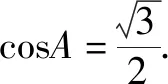
由余弦定理：a2=b2+c2-2bccosA，

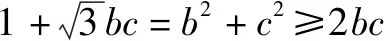
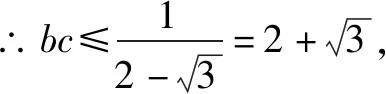
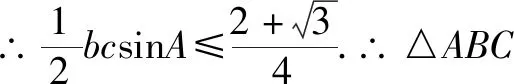
反思总结三角函数综合题有时以向量为背景进行命制，比如结合向量的坐标运算、向量垂直与平行的充要条件、向量的数量积等等，其本质依然是考察三角恒等变换或者三角函数的图象和性质.对于这类问题，我们的基本策略是将向量条件等价转化为三角条件，即关于三角形中边角的三角方程或者表达式，然后依照案例的方法就可以解决.

练一练D：

1.在△ABC中，AB=7,BC=5,AC=6,则AB·BC等于( ).

A.19 B.-19 C.18 D.-18

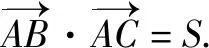
(1)求tan2A的值；

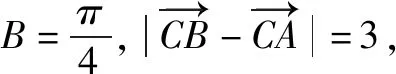
练一练D答案：

1.解析∵AB=7，BC=5，AC=6，

故选B.

2.(1)设△ABC的角A,B,C所对应的边分别为a,b,c.

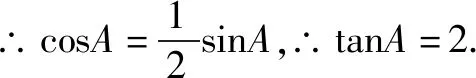
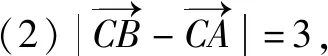
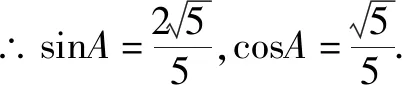
∴sinC=sin(A+B)=sinAcosB+cosAsinB

由正弦定理知：