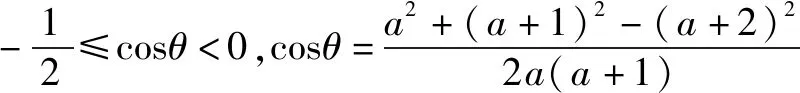在三角求值问题时要注意角的取值范围

田素伟

(上海泥城中学 201306)

在三角求值问题时很多同学由于忽略角的取值范围或是求错了角的取值范围而导致解题错误，如何能在解决这类三角求值问题时正确把握角的角的取值范围哪？下面就这个问题，举例说明：

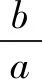
解由正弦定理

a=2RsinA、b=2RsinB可知，

∵△ABC是锐角三角形且B=2A.

评析边化为角时常用正弦定理，本题要充分挖掘寻找题中角的限制条件，求出角A的取值范围，很多学生常忽略角C的取值范围，要注意锐角三角形中三个内角都是锐角这一条件.

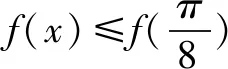
(1)求函数y=f(x)的解析式并写出其单调递增区间；

(2)若x为△ABC的最小内角，求函数y=f(x)的值域.

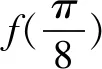
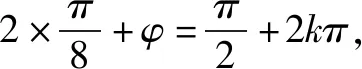
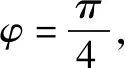
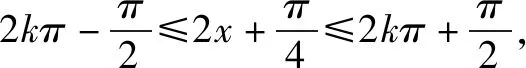
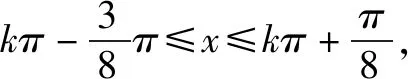
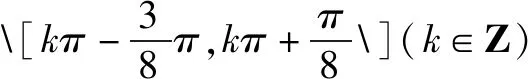
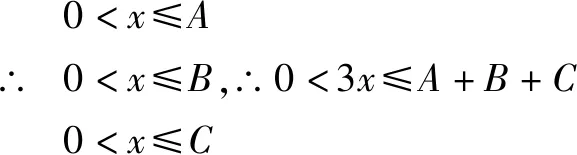
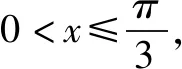
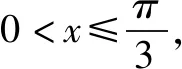
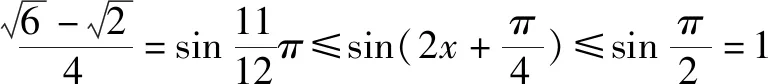
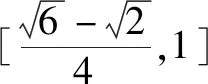
评析：本题中要明确△ABC的最小内角的取值范围，很多学生由于不理解最小内角的取值范围的推导，经常记错△ABC的最小内角的取值范围，本题考察在明确△ABC的最小内角的取值范围的前提下求给定区间的三角函数的最值和三角函数的性质.

例3在锐角三角形ABC中，若tanA=t+1，tanB=t-1，求t的取值范围.

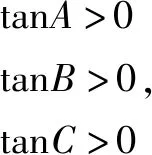
评析很多学生容易忽略角C的取值范围即tanC>0这一隐含条件导致解题错误.

要注意锐角三角形中三个内角都是锐角这一条件.

下面给出3道练习题，请同学练习

1.设锐角三角形ABC的内角A、B、C的对边分别为a,b,c,且bcosC=(2a-c)cosB.

(1)求角B的大小;

(2)求sinA+sinC的取值范围.

2.锐角△ABC中已知两边a=1,b=2，则第三边c的取值范围是____.

3.钝角三角形三边长为a,a+1,a+2,最大内角不超过120°，则a范围是____.

简答：

1.解(1)由条件及正弦定理得:

sinBcosC=(2sinA-sinC)cosB.

则sinBcosC+sinCcosB=2sinAcosB,

∴sin(B+C)=2sinAcosB,又sin(B+C)=sinA≠0,

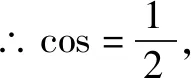
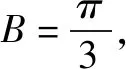
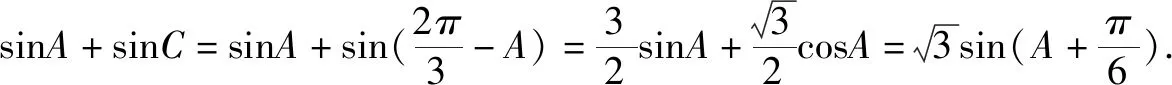
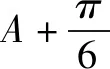
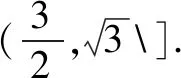
2.c2=5-4cosC∈(1,5),又B<90°,∴cosC>0,