再现椭圆定义 渗透核心素养

李小蛟

(四川省成都市树德中学 610091)

一、考题再现

(2)由题意得F(1,0),设P(x3,y3),则(x3-1,y3)+(x1-1,y1)+(x2-1,y2)=(0,0).

由(1)及题设得x3=3-(x1+x2)=1,y3=-(y1+y2)=-2m<0.

(1)求C的方程，并说明C是什么曲线.

(2)略.

即轨迹C为中心在坐标原点，焦点在x轴上的椭圆，不含左右顶点.

二、追本溯源

1.椭圆的第一定义

(1)

两边再次平方可得a2y2+(a2-c2)x2=a2(a2-c2)

(2)

两边同时除以a2(a2-c2)，

令b2=a2-c2，

2.椭圆的第二定义

平面上到定点距离与到定直线间距离之比为常数的点的集合(定点不在定直线上，该常数为小于1的正数)，该定点为椭圆的焦点，该直线称为椭圆相应焦点的准线.

这一定义又称为圆锥曲线的统一定义，在我们现行教材人教A版选修2-1中没有提出来，但有所呈现.

所以，点M的轨迹是长轴，短轴分别为10，6的椭圆.

3.椭圆的第三定义

平面内的动点到两定点A1(-a,0),A2(a,0)的斜率乘积等于常数e2-1的点的轨迹叫做椭圆.

这一定义也在我们现行教材人教A版选修2-1中同样没有提出来，但有所呈现.

解析设点M(x,y)，∵(-5,0),(5,0)

4.椭圆第二第义、第三定义的追本溯源

现行教材对椭圆的定义仅仅以第一定义的形式出现，第二定义、第三定义并没有给出正式定义，只是在教材例题中有所呈现.那么这三个定义之间是否有着必然的联系与完全的统一呢，让我们再从第一定义推导标准方程中去认真探究.

(3)

我们再看一下式a2y2+(a2-c2)x2=a2(a2-c2)，

移项可得a2y2=(a2-x2)(a2-c2)，

这即为椭圆的第三定义(平面内的动点到两定点A1(-a,0),A2(a,0)的斜率乘积等于常数e2-1的点的轨迹叫做椭圆).

三、迁移延伸

设A1(x1,y1),A2(x2,y2)为椭圆C上关于原点对称的任意两点，任取椭圆C上一点M(x,y)，若kMA1,kMA2均存在，则kMA1·kMA2=e2-1为定值.

分析∵A1,A2关于原点对称，∴x1=-x2,y1=-y2

又∵A1(x1,y1),M(x,y)在椭圆上，

显然椭圆第三定义实质上是这一延伸结论的特例.

四、拓展应用

解析一解析几何问题中求角三解形角度的最值，我们应选取这一角的某一三解函数值求解，由于正弦函数在(0,π)内不单调，而余弦函数严格单调递减.记∠F1PF2=θ,于是我们求解θ的余弦值.

解析二接解析一

在2.4中根据椭圆第二定义我们得到了椭圆的右焦半径公式|PF2|=a-ex，同理可行左焦半径公式|PF1|=a+ex.

根据题意，当x=0，即P为短轴上的顶点时，cosθ取得最大值，θ取得最小值，得证.

解析三本问题还可运用椭圆焦点三解形的面积公式求证.

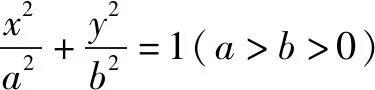
椭圆三个定义相互依存，相互联系，对椭圆三个定义的再现过程实质是就是学习解析几何用坐标来理解图形，对其相互联系的呈现既有解析几何运算的处理，也有转化与化归、数形结合等数学思想方法的体现，更重要的是在定义的推导，联系、运用、延伸、拓展中对数学抽象、逻辑推理、数据处理、数学运算等核心素养的渗透和发展.