例谈数据一般化方法的应用

刘大鹏

(辽宁省黑山县第一高级中学 121400)

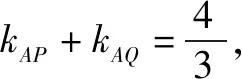
一、将数据一般化，探究定点坐标的表达式

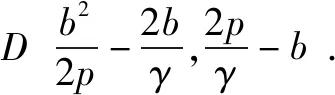
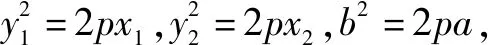
∴2p(2b+y1+y2)=γ[b2+b(y1+y2)+y1y2],

①

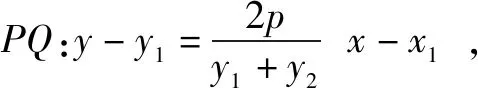
∴(y1+y2)y-y1y2=2px

②

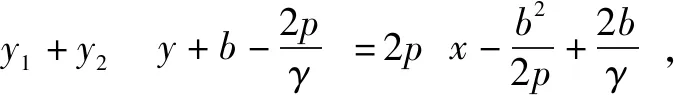
引例2(2013晋中名校联考)已知点A(x1,y1),B(x2,y2)是抛物线y2=4x上相异两点，且满足x1+x2=2,①略②若AB的垂直平分线交x轴于点M，求三角形AMB的面积的最大值及此时直线AB的方程.

二、将数据一般化，探究三角形面积最大值的表达式

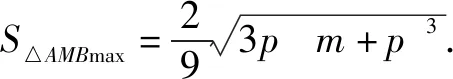
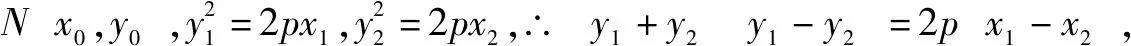
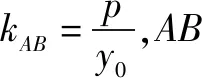
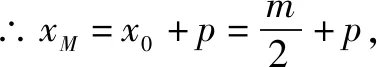
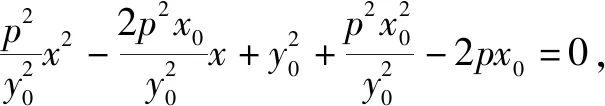
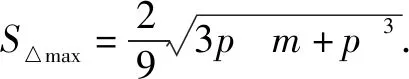
解法二由解法一得

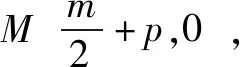
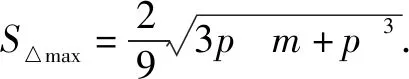
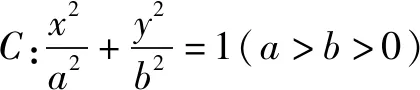
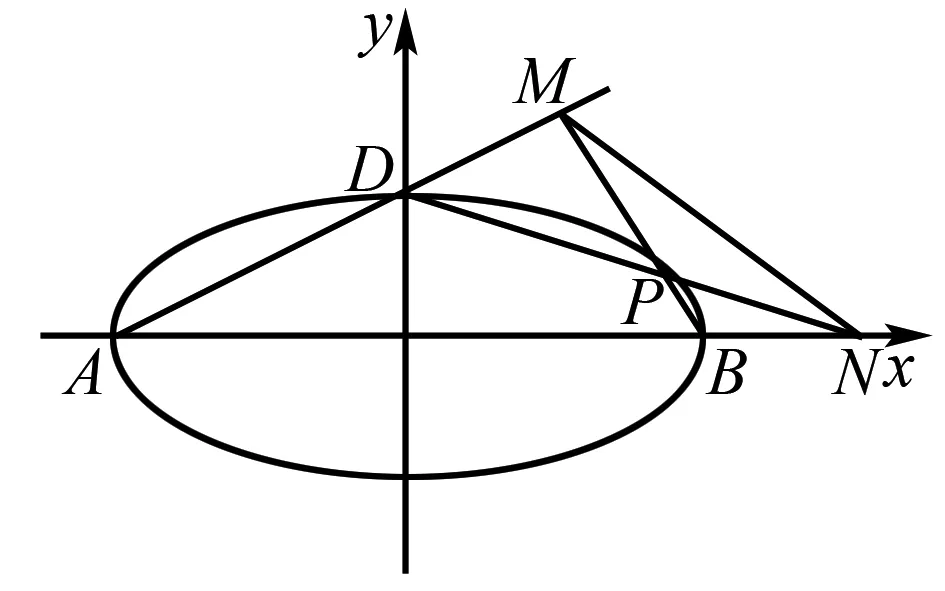
①求椭圆C的方程，②如图A,B,D是椭圆C的顶点，P是椭圆C上除顶点外的任意一点，直线DP交x轴于点N，直线DA交BP于点M，证明:2kMN-kBP为定值.

三、将数据一般化，探究定值的几何意义

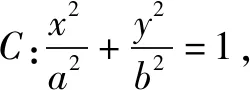
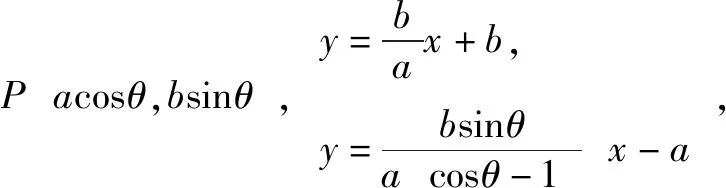
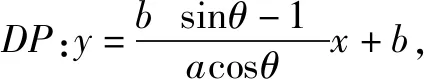
为定值.此定值是直线AD的斜率.即kAD,kMN,kBP成等差数列.

下面的题目留给读者练习

强化训练

请读者将题目中的数据一般化，从而找到隐藏在题中的圆锥曲线性质，并给出证明.

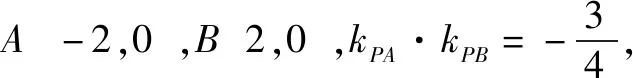
①求动点P的轨迹C的方程；

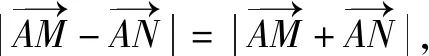
数据一般化的思维方法有利于培养思维的深刻性，有利于摒弃题海战术，有利于提高学习效率，在解析几何领域大有用武之地，希望本文对培养学生数学兴趣、提高师生数学核心素养方面能有所帮助.