从“乘1法”到待定系数法

谢贤祖

(广东省汕尾市华南师大附中汕尾学校 516600)

一、问题起源

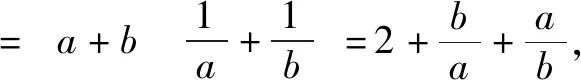
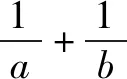
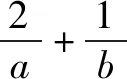
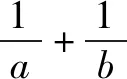
题4(造1法)已知a,b∈R+,a+3b=5ab，求3a+4b的最小值.

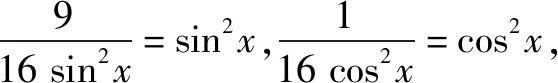
评注这道题考查得更加隐蔽，没有直接给出条件“1”，所以需要我们主动利用sin2x+cos2x=1来帮忙解题，最终使基本不等式得以使用，值得注意的是要验证取等条件，确保使用两次基本不等式后等号可以同时成立.下面再看一个“加1法”的升级版.

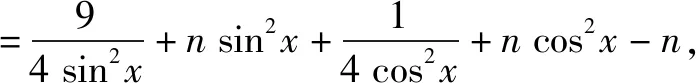
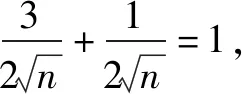
二、扩展延伸

由前面的例题展示，可以发现“用1”法的具体使用方向可以是：加、减、乘、除、代、造，尤其是“加n法”，其实就是待定系数版的基本不等式，更是解决竞赛不等式的利器.在遇到用基本不等式求最值的陌生题目，条件有出现“1”时，我们都可以尝试一下这些解题方向，不应该只局限于“乘1法”，遇到困难再切换方法.其实“1”可以去到目标式子里的任何位置，只要对我们的解题有简化作用，都可以尝试一下，下面继续举例说明.

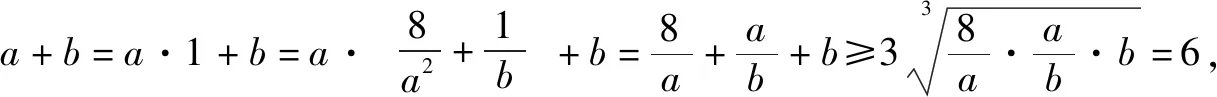
评注正如前文总结，“1”可以去到目标式子里的任何位置，只要对我们的解题有简化作用，如果一种方法遇到困难，我们需要继续调整策略，直至解题成功.下面再看一个用“代1法”来分析不等式的例子.

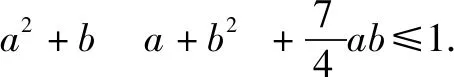
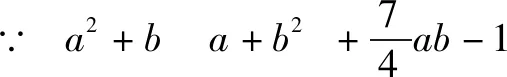
=0.

评注“1”可以去到目标式子里的任何位置，把“1”代入不等式中的一次项是为了实现“齐次化”，使得不等式的各项次数统一，容易化简.

受到前面题6的启发，可以考虑使用“加n法”.

原式

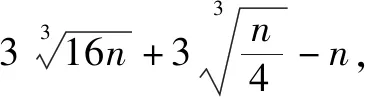
三、方法升级

前面的例题，笔者更多的是展示“加n法”，而且都是往缩小的方向使用平均值不等式，其实待定系数法的思想(也叫“平衡系数法”)在不等式中的应用很广泛，不应该只局限于前文所展示的这些方法.下面举例说明，继续发散思维，希望对读者有所帮助.

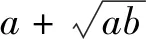
待定系数法还可以用到柯西不等式中.设x,y>0且x2+y2=1，

由柯西不等式得

≥a+ax+by=(1+x)a+yb

为了能够使用条件2a+b=2，使得(1+x)a+yb为定值，令(1+x):y=2:1，结合x2+y2=1，

四、总结反思

通过前面这一系列从易到难的例题展示，我们可以总结“用1法”的具体使用方向是：加、减、乘、除、代、造等等，还有待定系数法的作用更是强大，可以为我们解决最值问题指明方向，但一定要小心确认一下取等条件是否合理，以上的每道例题笔者都亲自计算确认无误，限于篇幅，验证取等条件的过程被笔者舍去，读者可以自行验证.