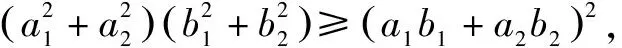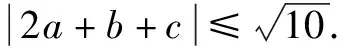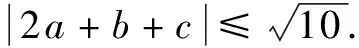不等式证明的几种解题方法
汤晓玲
(江苏省海门中学 226100)
一、通过作差来比较
要想证明a 例1 给定一个集合,M∈{x|-1 证明(a+b)2-(1+ab)2=a2+2ab+b2-(1+2ab+a2b2)=a2-1+b2(1-a2)=(a2-1)(1-b2). 由题可知,a的取值范围是-1 评析此题将平方作差法和因式分解法相结合,进一步确定在a,b∈M这个范围内,a2-1和1-b2的符号,借此来证明|a+b|<|1+ab|这个不等式是成立的. 小结作差比较法和作商比较法可以归纳为一类:比较法.比较法常用于处理多项式的大小的比较等相关问题,作差比较和作商比较是比较法中使用频率最高的两者方法.使用作差比较法时一般是求被证明的不等式的两端是分式、多项式和对数式;而使用作商比较法时,一般是求被证明的不等式的两边含有指数式、幂式或乘积式. 类似a2+b2≥2ab等题型,可以利用均值不等式进行分析. 例3若a,b满足条件a>0,b>0,且有a3+b3=2.证明a+b≤2. 所以(a+b)3≤8. 所以a+b≤2. 例4 已知有三个数x,y,z,且x>0,y>0,z>0,xyz=1,求证:x3+y3+z3≥xy+yz+xz. 证明由题意可以得到:x>0,y>0,z>0, 因此有:x3+y3+z3≥3xyz, x3+y3+1≥3xy, y3+z3+1≥3yz, x3+z3+1≥3xz. 把上述各个式子相加可以得到: 3x3+3y3+3z3+3≥3xyz+3xy+3yz+3xz. 又已知xyz=1,所以x3+y3+z3≥xy+yz+xz. 证明根据柯西不等式可以得到: 根据题目中的条件可以知道:4a2+b2+2c2=4. 因此我们可以进一步求得(2a+b+c)2≤10. 不等式两边同时开方,得 评析将原不等式转化成符合柯西不等式的结构以及要学会适宜的变形是使用柯西不等式证明的关键所在,要想使用柯西不等式对一个式子进行放大或者缩小就要求这个式子的左右任意一边要与柯西不等式具有相类似的形式,进而使得需要求证的问题得到证明. 小结通过分析可以发现,也可以将方法3、方法4、方法5进行一个归纳总结,将这三个方法归纳为综合法.证明不等式的最根本的方法之一就是综合法,综合法主要通过利用不等式的相关性质、实数的相关性质、已知的不等式等来进行证明.这几个相关性质是使用综合法的核心.根据“据因得果”的方法,利用已知的条件进行综合推理就能得出题目要求证明的不等式.其中最常使用的是不等式的相关性质和基本不等式,在运用这些性质进行解题时,要时刻关注这些性质成立的前提要求. 本篇文章主要对不等式证明的方法进行了探究和分析,在实际运用中,应该根据实际情况和解题的实际需要选择恰当的方法.关于不等式的证明方法是多种多样的,上述方法只是其中的几种,当题目表述简单明了,有较为清晰的条理时,就可以尝试用综合法求证,给定的代数式中存在有“和式”或者存在有“积式”时,那么此代数式的“题眼”就已知了,便可利用基本不等式求证.不等式的证明方法灵活,形式多样,需要同学们更多地拓展思维,灵活使用学习的知识去解题.二、利用作商来比较
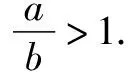
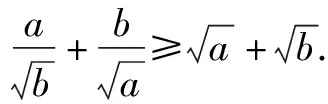


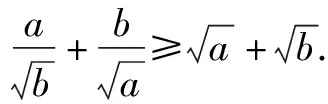
三、基本不等式及其变式法
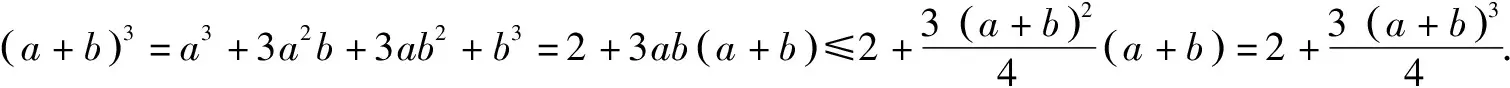
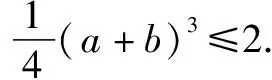
四、均值不等式法
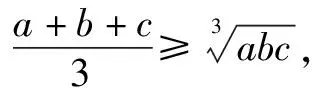
五、柯西不等式求解