论类比思维下的高中数学解题方法
张 宇
(福建省福州延安中学 350001)
所谓类比思维是指根据两个对象在某些属性上相同或相似,通过比较而推断出它们在其他属性上也相同的推理过程.高中数学解题中,在类比思维指引下可使学生尽快找到解题思路,提高解题效率,因此要认识到类比思维的重要性,为学生讲解类比思维在解题中的具体应用,使学生掌握相关的应用方法与技巧.
一、类比思维下方程习题的解答
众所周知,函数与方程有着密切的联系.对于无法直接求解方程根的习题,可通过转化为函数图象交点的问题进行突破.教学中为使学生掌握求解特殊方程根的方法,应结合学生所学知识,设计新颖的问题情境,鼓励学生运用类比思维进行解答,使其在认识到类比思维的重要性的同时,进一步拓展其视野,积累求解方程根的新思路.
例1求“方程log2x+log3x=0的解”时,可设函数f(x)=log2x+log3x,则函数f(x)在(0,+∞)上单调递增,且f(1)=0,因此原方程有唯一解x=1.类比上述思路,则方程(x-1)5+x-1=34的解集为____.
由于方程的根是对应函数与x轴交点的横坐标,因此在解答该高次方程时需要从题干中得到启示,进行合理类比,即先判断对应函数的单调性,从整体上把握方程根的个数,而后结合自身经验找到方程的根.该题难度并不大,解题思路可通过类比获得,判断高次函数单调性可借助导数进行分析.
根据给出的思路进行类比,令f(x)=(x-1)5+(x-1)-34,对其进行求导得到f′(x)=4(x-1)4+1,可知在x∈R上f′(x)>0,表明函数f(x)在x∈R上单调递增,即f(x)和x轴只有一个交点,方程只有一个实根.又因为25+2=34,因此,x-1=2,解得x=3,则原方程的解集为{3}.
二、类比思维下几何习题的解答
在平面几何中有很多与立体几何相类似的性质,在教学中可鼓励学生认真思考,推导平面几何中的一些性质是否在立体几何中也适用.为激发学生探究的热情,可从平面几何结论入手自然引入立体几何问题,要求学生运用类比思维进行分析、解答,亲身感受类比的过程,积累运用类比思维解题的经验.

该题目以学生熟悉的平面几何知识为切入点,要求其通过类比推导出立体几何中的相关结论,既能巩固学生所学,又能很好地锻炼学生的类比推理能力.该题目给出的已知条件并不多,解答时应能透过现象看本质,大胆设出相关参数,运用所学进行严谨的推理.
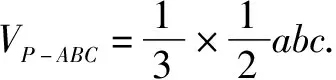
类比可知
VP-ABC=VO-ABC+VO-PAB+VO-PAC+VO-PBC
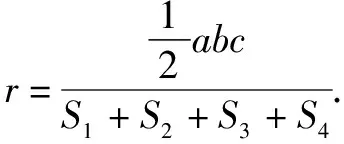



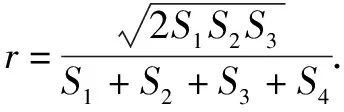
三、类比思维下数列习题的解答
数列是高中数学的难点知识,包括等差数列与等比数列,两者之间有着类似的性质.因此,一些测试中常涉及两者之间进行类比推理的习题,检验学生对数列知识的理解深度以及思维的灵活性.为了深化学生对数列知识的理解,掌握相关的解题方法,教学中应向学生展示一些经典习题,组织学生开展针对性训练活动,鼓励学生通过类比解答.

解题时要求认真分析已知条件中等差数列之和与项数之间的关系,吃透题意,把握其本质.如果学生不知如何下手,那么教学中可以引导学生先类比其“形”,猜想结论,必要情况下可代入特殊的数列进行验证,若类比的结论正确,再运用所学知识进行证明.
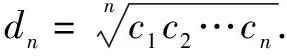
为使学生能够灵活运用类比思维正确解答相关数学习题,促进学生提升解题能力,教学中既要注重灌输相关的理论,使学生把握类比的思路以及注意事项,又要围绕例题,为学生做好解题示范,并鼓励其做好听课总结,真正消化、吸收所学,在解题中养成应用类比思维解题的习惯,不断提高思维的灵活性,真正掌握这一重要的解题思维.

