高考试题“充分与必要条件”归类赏析
廖永福
(福建省厦门第二中学 361009)
判断充分条件与必要条件,本质上就是判断命题的真假,常用的方法有:
1.定义法:若p⟹q,则p是q的充分条件,q是p的必要条件;若p⟺q,则p是q的充要条件,q也是p的充要条件.口诀:箭尾充分,箭头必要.
2.集合法:设A={x|x满足条件p},B={x|x满足条件q},若A⊆B,则p是q的充分条件,q是p的必要条件;若A=B,则p是q的充要条件.口诀:小充分,大必要,等充要.
3.等价法:应用等价的传递性,即“若p⟺q且q⟺r,则p⟺r”.
充分条件与必要条件涉及的知识面较广,常与函数、三角函数、平面向量、数列、不等式和立体几何等知识相结合.
一、以函数知识为载体
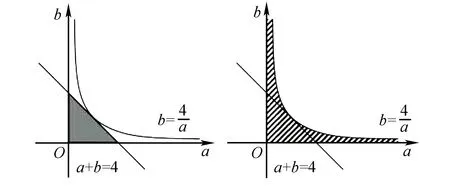
例1 (2020·上海卷)命题p:存在a∈R且a≠0,对于任意的x∈R,使得f(x+a) 命题q1:f(x)单调递减且f(x)>0恒成立; 命题q2:f(x)单调递增,存在x0<0使得f(x0)=0,则下列说法正确的是( ). A.只有q1是p的充分条件 B.只有q2是p的充分条件 C.q1,q2都是p的充分条件 D.q1,q2都不是p的充分条件 分析用定义法,只要判断命题“若q1,则p”和命题“若q2,则p”的真假即可. 解析若q1成立,当a>0时,x+a>x,因为f(x)单调递减且f(x)>0恒成立,所以f(a)>0,所以f(x+a) 综上可知,q1,q2都是p的充分条件,故选C. 点评本题以函数知识为背景,主要考查充分条件的判断,函数单调性的应用,考查推理和运算能力等,解题关键是把问题转化为判断两个命题的真假,属于中档题. 变式1 (2016·上海卷)设函数y=f(x)的定义域为R,则“f(0)=0”是“函数f(x)为奇函数”的( ). A.充分而不必要条件B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 变式2 (2016·浙江卷)已知函数f(x)=x2+bx,则“b<0”是“f(f(x))的最小值与f(x)的最小值相等”的( ). A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 答案:1.B 2.A 例2(2020·北京卷)已知α,β∈R,则“存在k∈Z使得α=kπ+(-1)kβ”是“sinα=sinβ”的( ). A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 分析用定义法,并对k的奇偶性进行讨论. 解答当k=2n(n∈Z)时,α=2nπ+β,此时sinα=sin(2nπ+β)=sinβ;当k=2n+1(n∈Z)时,α=2nπ+π-β,此时sinα=sin(π-β)=sinβ,即充分性成立. 若sinα=sinβ,则α=2nπ+β或α=2nπ+π-β(n∈Z),即α=kπ+(-1)kβ,即必要性成立. 所以,“存在k∈Z使得α=kπ+(-1)kβ”是“sinα=sinβ”的充要条件,故选C. 点评本题以三角函数知识为背景,主要考查充分条件和必要条件的判断,考查诱导公式和三角函数性质的应用,考查分类讨论思想等,解题关键是对k的奇偶性进行讨论,属于基础题. 变式1 (2020·上海卷)“α=β”是“sin2α+cos2β=1”的( ). A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件 变式2 (2019·北京卷)设函数f(x)=cosx+bsinx(b为常数),则“b=0”是“f(x)为偶函数”的( ). A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 答案:1.A 2.C A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 分析用等价法,结合向量的减法公式和向量的运算法则即可作出判断. 点评本题以向量知识为背景,主要考查充分条件和必要条件的判断,考查平面向量的模、夹角与数量积,考查推理和运算能力等,解题关键是对题设条件进行等价转化,属于基础题. 变式1 (2018·北京卷)设a,b均为单位向量,则“|a-3b|=|3a+b|”是“a⊥b”的( ). A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 变式2 (2017·北京卷)设m,n为非零向量,则“存在负数λ,使得m=λn”是“m·n<0”的( ). A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 答案:1.C 2.A 例4 (2016·天津卷)设{an}是首项为正数的等比数列,公比为q,则“q<0”是“对任意的正整数n,a2n-1+a2n<0”的( ). A.充要条件 B.充分而不必要条件 C.必要而不充分条件 D.既不充分也不必要条件 分析用集合法,先求出“q<0”和“对任意的正整数n,a2n-1+a2n<0”对应的集合,再根据两个集合之间的包含关系作出判断. 解答a2n-1+a2n=a1q2n-2(1+q),a1q2n-2>0.若对任意的正整数n,a2n-1+a2n<0,则1+q<0,解得q<-1. 因为“q<0”对应集合{q|q<0},“对任意的正整数n,a2n-1+a2n<0”对应集合{q|q<-1},且{q|q<0}{q|q<-1},所以“q<0”是“对任意的正整数n,a2n-1+a2n<0”的必要而不充分条件,故选C. 点评本题以数列知识为背景,主要考查充分条件和必要条件的判断,考查等比数列的定义和性质,考查推理和运算能力,解题关键是把问题转化为研究两个集合之间的关系,属于基础题. 变式1 (2018·北京卷)设a,b,c,d是非零实数,则“ad=bc”是“a,b,c,d成等比数列”的( ). A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件 D.既不充分也不必要条件 变式2 (2018·上海卷)设Sn为数列{an}的前n项和,“{an}是递增数列”是“{Sn}是递增数列”的( ). A.充分非必要条件B.必要非充分条件 C.充要条件 D.既非充分又非必要条件 变式3 (2017·上海卷)已知a,b,c为实常数,数列{xn}的通项xn=an2+bn+c,n∈N*,则“存在k∈N*,使得x100+k,x200+k,x300+k成等差数列”的一个必要条件是( ). A.a≥0 B.b≤0 C.c=0 D.a-2b+c=0 答案:1.B 2.D 3.A 例5 (2019·浙江卷)若a>0,b>0,则“a+b≤4”是“ab≤4”的( ). A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 分析若用定义法,只要判断命题“若a>0,b>0,a+b≤4,则ab≤4”和“若a>0,b>0,ab≤4,则a+b≤4”的真假即可;若用集合法,则应先求出“a>0,b>0,a+b≤4”和“a>0,b>0,ab≤4”对应的集合,再确定它们之间的包含关系,最后得出结论. 所以“a+b≤4”是“ab≤4”的充分不必要条件,故选A. 解法2集合M={(a,b)|a>0,b>0,a+b≤4}表示的平面区域为图1中的阴影部分,集合M={(a,b)|a>0,b>0,ab≤4}表示的平面区域为图2中的阴影部分. 图1 图2 由此可见MN,所以“a+b≤4”是“ab≤4”的充分不必要条件,故选A. 点评本题以不等式知识为背景,主要考查充分条件和必要条件的判断,考查基本不等式的应用,考查推理与计算能力等,解题关键是把问题转化为判断两个命题的真假或判断两个集合之间的关系,属于基础题. 变式1 (2020·天津卷)设a∈R,则“a>1”是“a2>a”的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 变式2 (2019·天津卷)设x∈R,则“x2-5x<0”是“|x-1|<1”的( ). A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 A.充分非必要条件 B.必要非充分条件 C.充要条件 D.既非充分又非必要条件 A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要条件 答案:1.A 2.B 3.A 4.A 例6 (2019·全国Ⅱ卷)设α,β为两个平面,则α∥β的充要条件是( ). A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行 C.α,β平行于同一条直线 D.α,β垂直于同一平面 分析用定义法,结合面面平行的判定定理和性质定理可得结论. 解析对于A,α内有无数条直线与β平行,α∩β或α∥β;对于B,α内有两条相交直线与β平行,α∥β;对于C,α,β平行于同一条直线,α∩β或α∥β;对于D,α,β垂直于同一平面,α∩β或α∥β.故选B. 点评本题以立体几何知识为背景,主要考查充分条件和必要条件的判断,考查面面平行的判定和性质,考查逻辑推理能力,属于基础题. 变式1 (2020·浙江)已知空间中不过同一点的三条直线l,m,n.则“l,m,n共面”是“l,m,n两两相交”的( ). A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 变式2 (2018·浙江卷)已知平面α,直线m,n满足m⊄α,n⊂α,则“m∥n”是“m∥α”的( ). A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 变式3 (2016·山东卷)已知直线a,b分别在两个不同的平面α,β内,则“直线a和直线b相交”是“平面α和平面β相交”的( ). A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 答案:1.B 2.A 3.A二、以三角函数知识为载体
三、以平面向量知识为载体
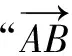

四、以数列知识为载体
五、以不等式知识为载体
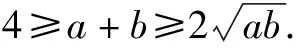



六、以立体几何知识为载体

