FRP复合材料工字梁结构性能研究*

李泳璋，吴 迪

(西安科技大学建筑与土木工程学院，陕西 西安 710054)

0 引言

FRP复合材料具有强度高、质轻、耐腐蚀等优点，但高昂的成本成为推广应用的障碍。本文提出将玻璃纤维(GFRP)与碳纤维(CFRP)结合的复合材料，即在混合复合材料中加入适量的CFRP/GFRP，既提高材料强度又降低使用成本。混合FRP复合材料在世界范围内进行大量的理论和试验研究。Summerscales等回顾碳-玻璃复合材料的许多研究，发现称为混合效应的现象。混合效应的观察归功于Hayashi，随后几位研究人员对此进行报道，但对混合梁的结构性能研究甚少。本文研究由多层碳纤维/E-玻璃纤维/乙烯基酯组成的混合FRP梁结构性能，以FRP工字梁为研究对象，通过梁的抗弯试验，研究混合FRP工字梁的结构性能，确定梁中CFRP和GFRP的最佳组成。

1 试验设计

试验在室内进行，所有横梁均采用树脂传递模塑工艺制造，由碳纤维-玻璃纤维/乙烯基酯树脂组成。试验2组不同的FRP工字梁，翼缘与腹板宽度之比(bf/bw)不同，NF为窄翼缘(bf/bw=0.43)，WF为宽翼缘(bf/bw=1.13)。工字梁尺寸如图1所示。在3 000mm跨度和1 000mm内部荷载跨度下，对梁进行简单支撑和4点弯曲试验。

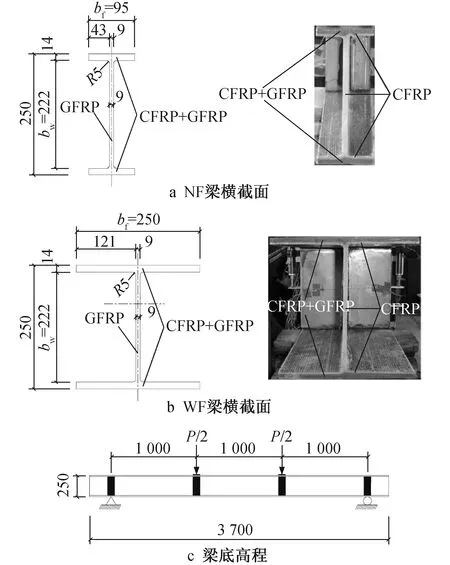
图1 FRP复合材料工字梁尺寸

所有工字梁的翼缘均由CFRP和GFRP制成，腹板仅由GFRP制成。腹板上的某些GFRP层延伸至每个梁翼缘。CFRP的角度相比纵向固定为0°，定义为CFRP-0；GFRP的角度固定为0/90°，±45°或多方向(连续纤维毡，CSM)，分别定义为GFRP-0/90，GFRP±45或GFRP-CSM，用来改善混合FRP层压板的机械性能。为从成本和强度角度研究合适的横梁设计，翼缘使用3种成分的碳纤维，含量分别为52%，33%，14%，如表1所示。本试验中使用的碳纤维和玻璃纤维力学性能如表2所示。腹板中安装钢制箱形加强筋，以防止支座处的挠曲和翘曲及加载点处的局部破坏[13]。测试设置和仪器如图2所示。

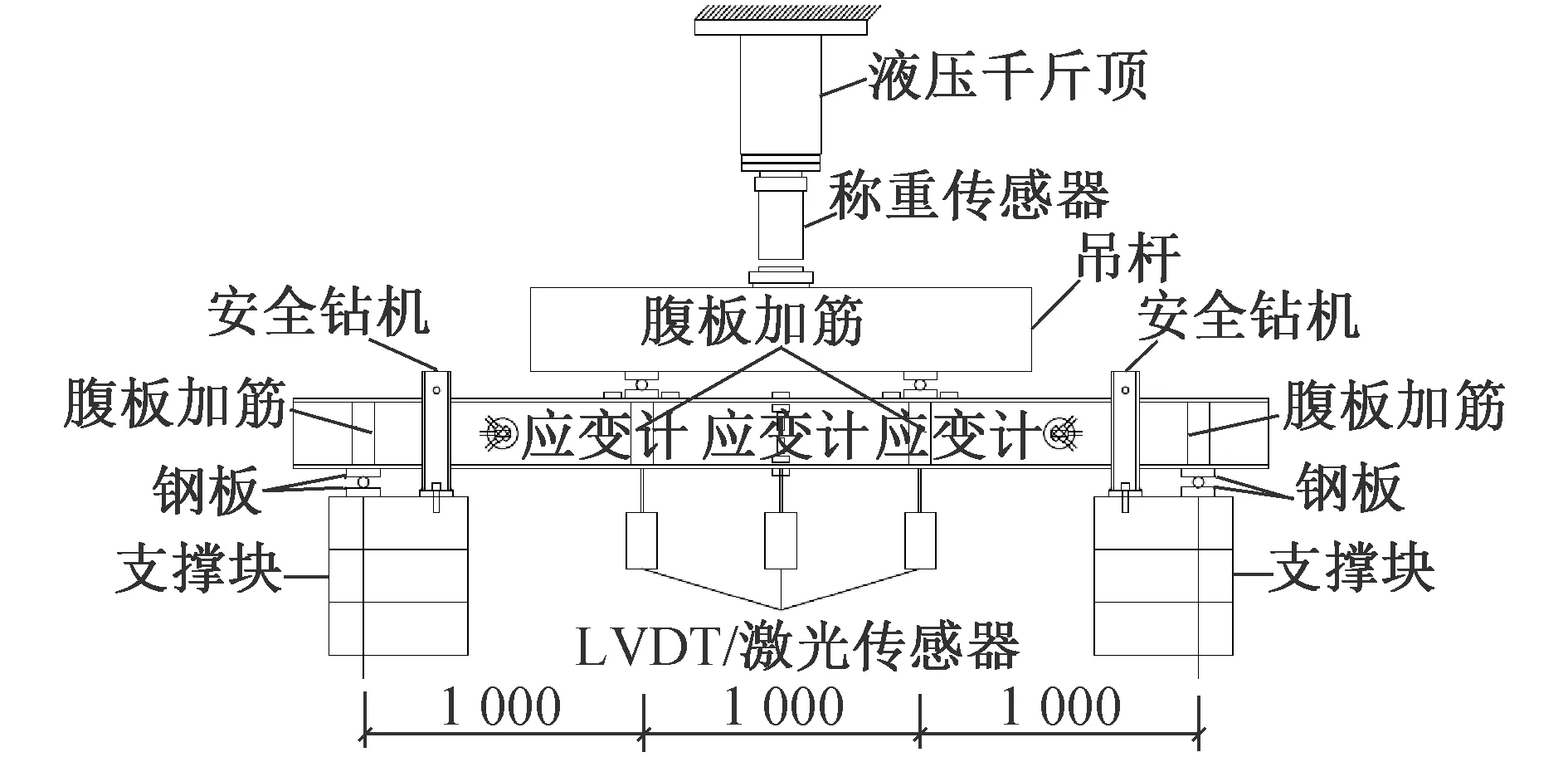
图2 测试设置和仪器

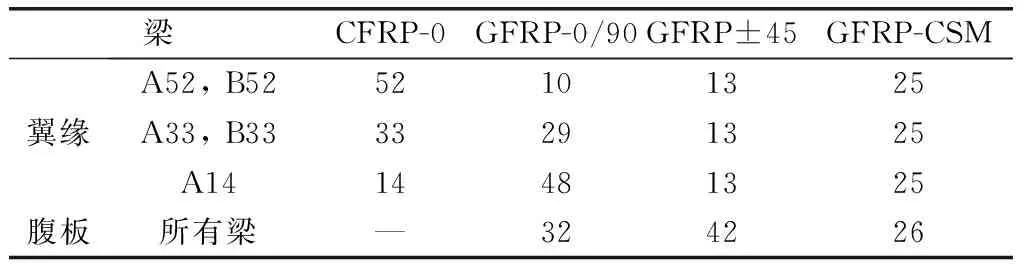
表1 FRP复合材料含量 %

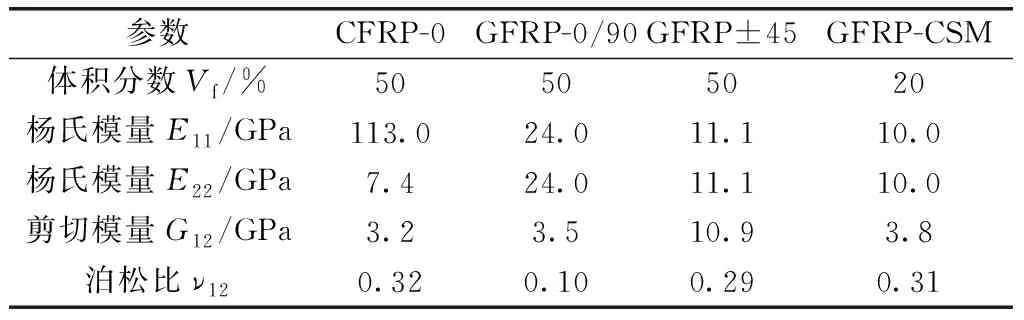
表2 材料力学性能

2 试验结果分析

2.1 NF梁抗弯性能分析

2.1.1荷载-挠度曲线

NF梁的荷载与跨中挠度关系如图3所示。可以看出，所有梁的性能几乎是线性的，直至失效，跨中截面处荷载-挠度曲线的斜率与翼缘中CFRP的体积含量成正比。

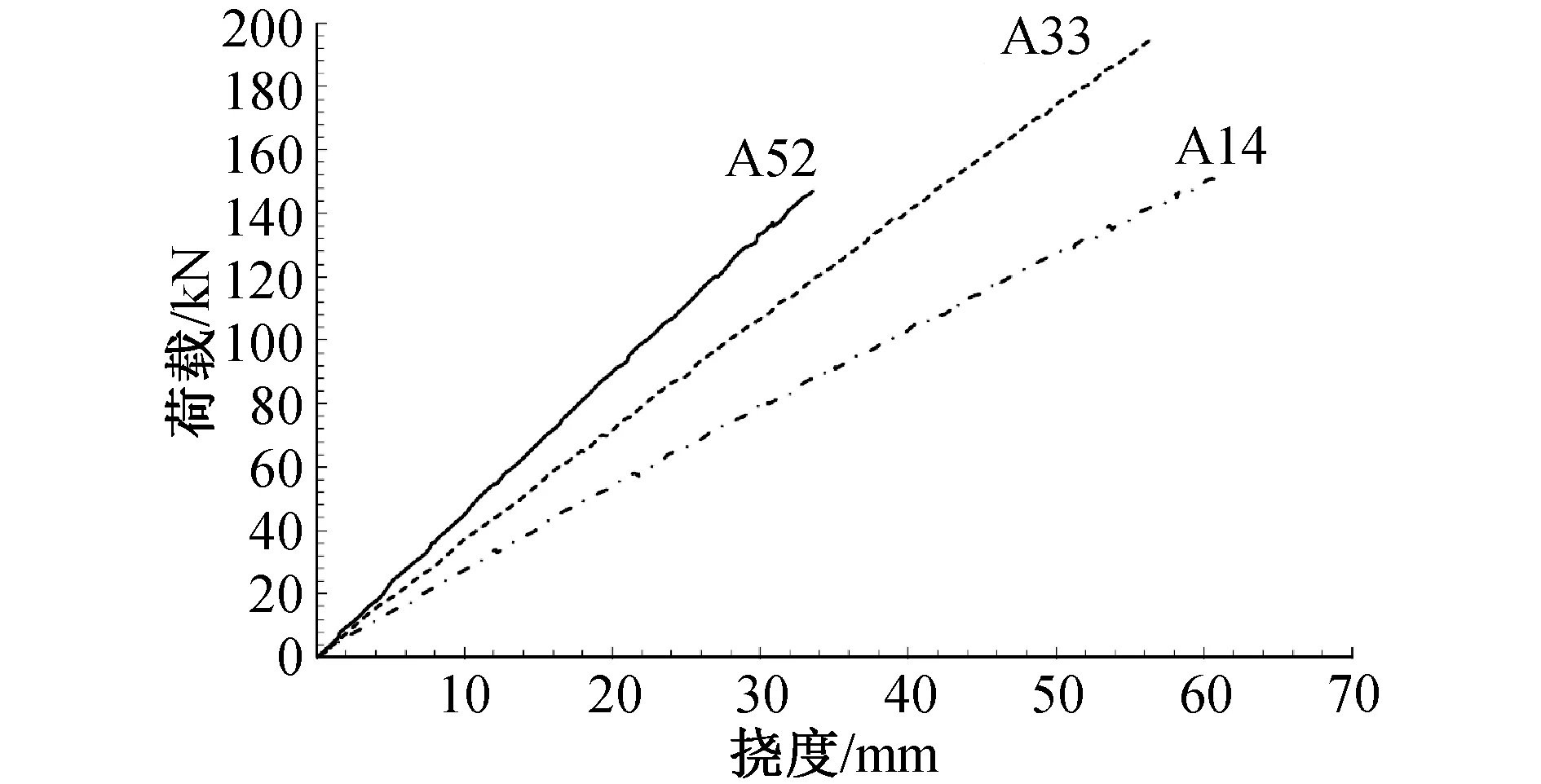
图3 NF梁荷载-挠度曲线

2.1.2荷载-应变曲线

荷载与跨中截面翼缘顶部与底部纵向应变间的关系如图4所示。结果表明，压缩应变和拉伸应变在破坏前均呈线性变化。梁A14中的最大压缩应变和拉伸应变值约为7 100με，约为40%的极限拉伸应变和70%的CFRP极限压缩应变，即碳纤维布的高强度不能有效应用于受拉翼缘，充分利用碳纤维布的强度优势还需进一步发展。

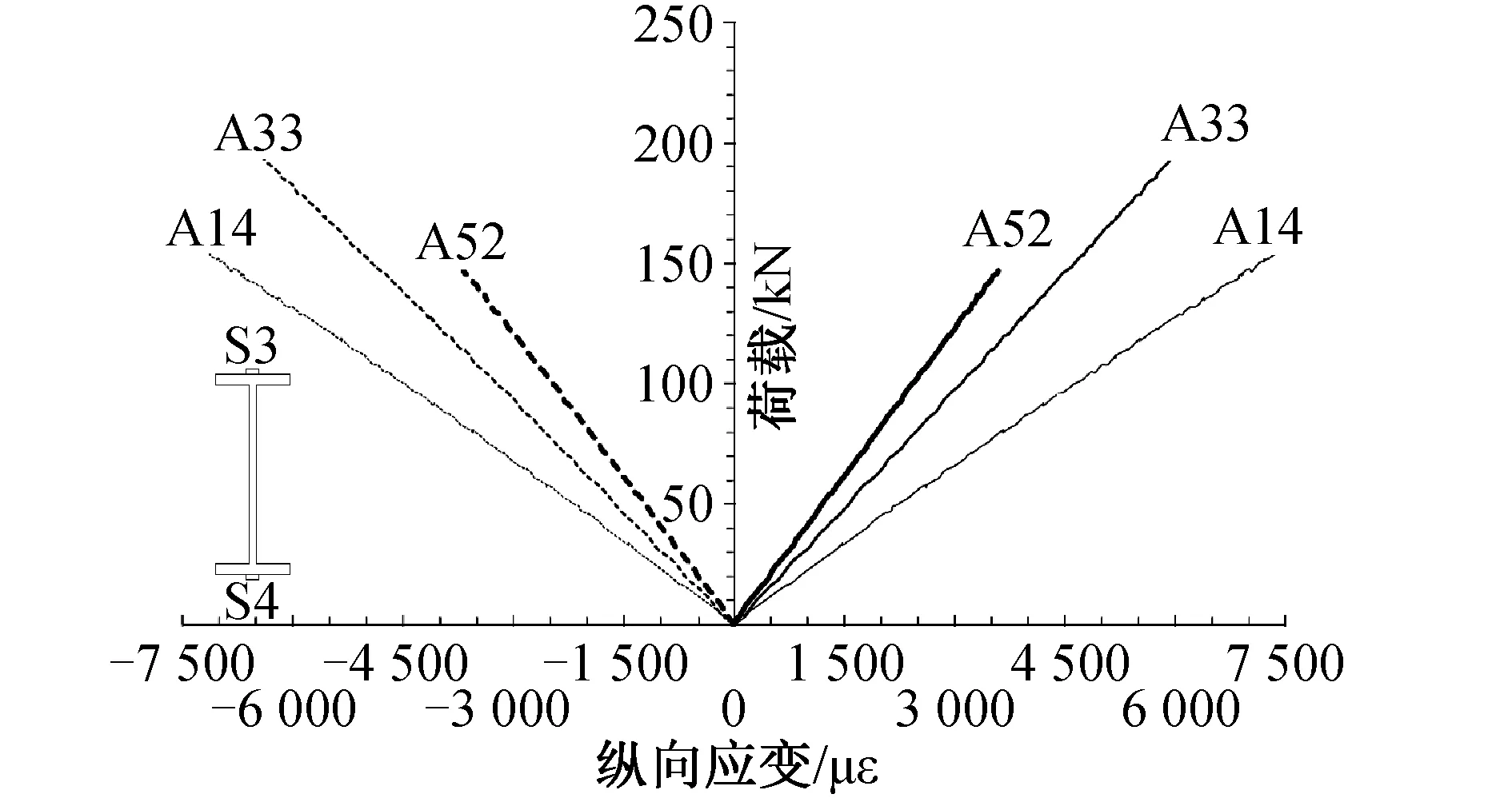
图4 NF梁翼缘荷载-纵向应变

腹板顶部和底部垂直应变如图5所示。腹板顶部的垂直应变为拉伸应变，腹板底部垂直应变为压缩应变。同一位置的水平和垂直应变与正泊松比(εy=-εxvxy)形成对比。因此，腹板顶部的水平应变是压缩应变，然后是拉伸垂直应变，腹板底部的情况正好相反。

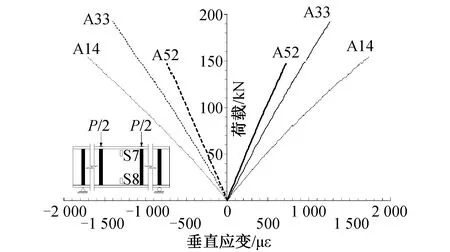
图5 NF梁腹板荷载-垂直应变

2.2 WF梁抗弯性能分析

2.2.1荷载-挠度曲线

WF梁测得的跨中截面荷载-挠度曲线如图6所示。B52，B33梁改变翼缘中CFRP的体积含量，在受压翼缘中观察到初始局部屈曲前，几乎呈线性行为，初始荷载高达200～210kN，破坏时的极限荷载几乎相同，为235kN。这些梁的最终破坏模式是受压翼缘的局部屈曲，导致翼缘层合板分离和腹板压碎。

图6 WF梁荷载-挠度曲线

2.2.2荷载-应变曲线

WF梁跨中截面上下翼缘处的荷载与纵向应变间的关系如图7所示。可以看出，当荷载超过200～210kN时，上翼缘的压缩应变表现为非线性，而下翼缘的拉伸应变对破坏呈线性响应，此外，梁的极限压缩应变和拉伸应变均未达到FRP材料极限应变。

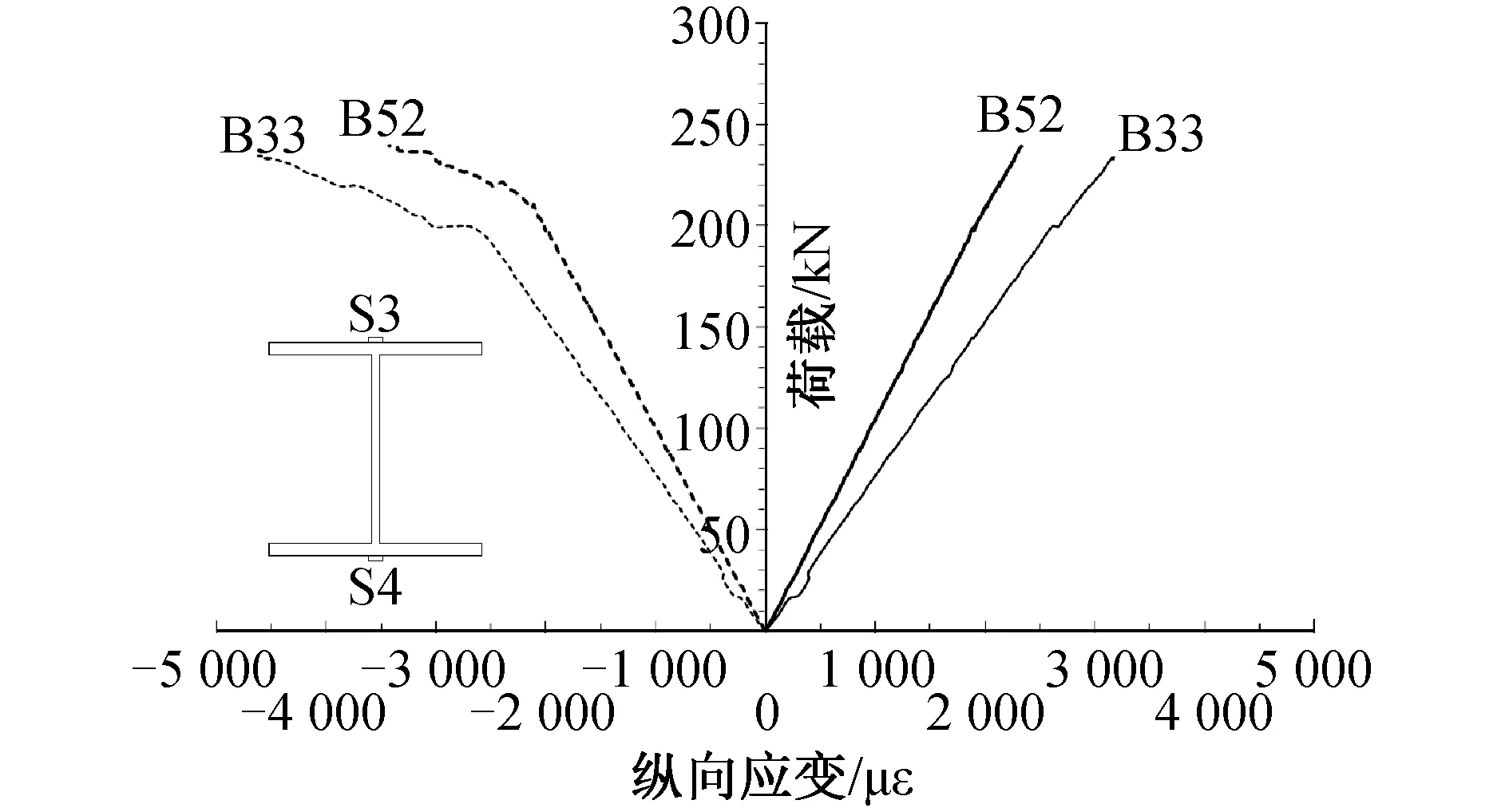
图7 WF梁翼缘荷载-纵向应变

B52，B33梁跨中截面顶部和底部腹板的垂直应变分布如图8所示。拉伸后的垂直应变在后屈曲区域中显著增加，在底部腹板中压缩应变的增加不显著(断裂处的极限拉伸应变约为5 000με，失效时的极限压缩应变仅1 300με)，即跨中截面腹板顶部的屈曲比腹板底部的屈曲更关键，腹板屈曲可能在受压翼缘屈曲后开始。

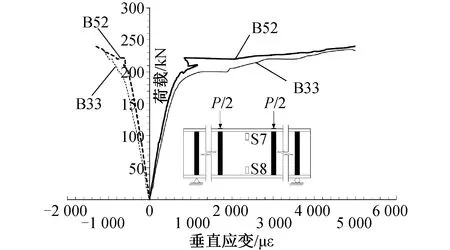
图8 WF梁腹板荷载-垂直应变

2.3 梁刚度计算

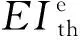
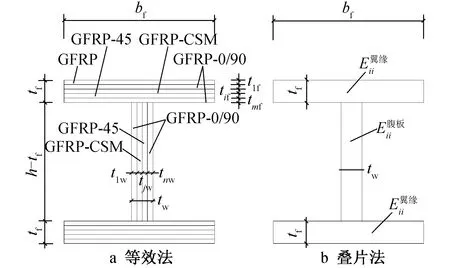
图9 变截面法计算转动惯量

(1)

(2)

(3)

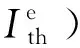
(4)

(5)

(6)

若If和Iw是翼缘与腹板的中性轴转动惯量(假设中性轴穿过梁截面的重心)，则M是凸缘总层，N是腹板总层。

(7)

(8)

式中：i为(1，m)，j为(1，n)；bf为翼缘宽度(mm)；tf为翼缘总厚度(mm)；tw为腹板总厚度(mm)；tif为翼缘i层厚度(mm)。

(9)

(10)

计算结果为：

(11)

(12)

(13)

(14)

式中：Eii根据CLT确定，E11和E22分别是翼缘或腹板在纵向和横向的等效杨氏模量；Aij是层压板的拉伸刚度；t是翼缘或腹板的厚度。

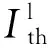
(15)

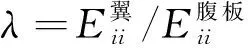
基于CLT的SF梁翼缘与腹板的杨氏模量E、剪切模量G和泊松比ν的计算值如表3所示。

表3 SF梁刚度计算汇总

3 有限元分析

3.1 有限元建模

本文讨论如何确定碳纤维布和玻璃纤维布的最佳组合，以便优化设计混合纤维布梁。采用非线性三维有限元分析方法研究NF梁的性能，该方法可精确求解混合FRP层合板的多层组合问题。使用MSC.Marc程序对NF梁进行建模。梁的翼缘和腹板采用8节点组合砖单元，每个翼缘46层碳纤维布、GFRP-0/90，GFRP-45和GFRP-CSM，腹板32层GFRP-0/90，GFRP-45和GFRP-CSM。加载点/支撑下的钢板和箱型加劲肋采用8节点砖单元建模。假设各层间存在完全复合作用。有限元几何结构和与局部坐标系11，22，33的网格如图10所示。有限元分析的输入数据如表4所示。通过比较试验结果，验证模型准确性。

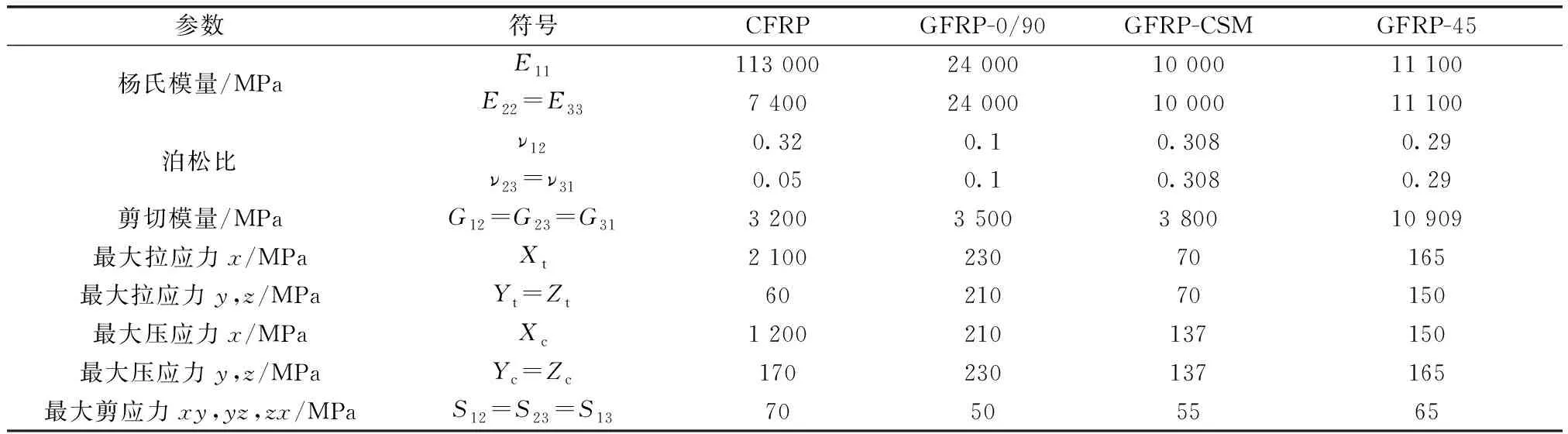
表4 有限元分析输入数据

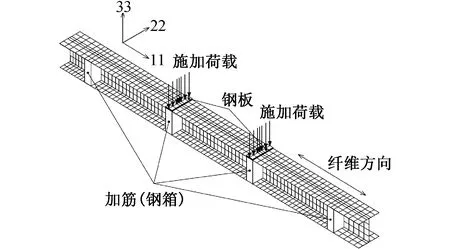
图10 有限元网格划分

3.2 有限元与试验结果对比分析

试验和有限元分析得到的NF梁荷载-挠度与荷载-应变曲线如图11，12所示。可以看出，有限元分析所得的荷载-挠度曲线与荷载-应变曲线及所有NF梁的试验结果基本相同。由表5可知，试验与有限元分析的平均破坏荷载差异<2%，并且2种方法得出的破坏模式相同，因此，有限元分析结果对预测混合FRP梁的强度具有重要意义。从表中可以看出，翼缘中含碳量不同所需的极限荷载也不同，其中梁A33所需极限荷载最大，梁A52次之，梁A14最小，因此有必要进一步确定含碳量，从而获得混合纤维复合材料的最大强度。

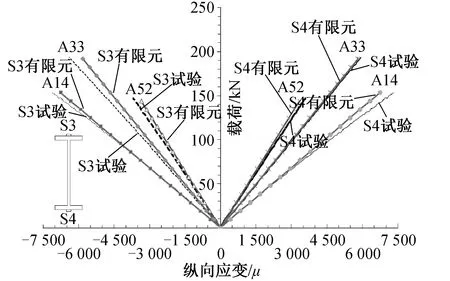
图12 荷载-NF梁上下翼缘的纵向应变

表5 有限元与试验结果比较

3.3 碳含量对梁破坏强度的影响

为确定翼缘中CFRP的最佳体积含量，对CFRP体积含量为5%～60%的NF梁进行参数化有限元分析。分析A5，A14，A25，A33，A45，A52，A60(每根梁表示CFRP在翼缘中的百分比)。

破坏荷载与CFRP体积含量间的关系如图13所示。可以看出，最大荷载随CFRP体积含量的增加而增加，从5%增加到25%。这一范围内，梁的破坏模式取决于跨中截面腹板中纤维的破坏。A25和A33梁的破坏荷载几乎相同，尽管这2个梁的CFRP体积含量相差8%。A25梁的破坏模式以跨中截面腹板的纤维破碎为主，A33梁的破坏模式是由于层间拉应力过大导致上翼缘分层。当CFRP体积含量从25%增加到33%时，破坏荷载不增加，但破坏模式可能由腹板压碎转变为分层。表明CFRP的最佳体积含量为25%～33%，建议在桥梁应用中设计FRP混合梁。

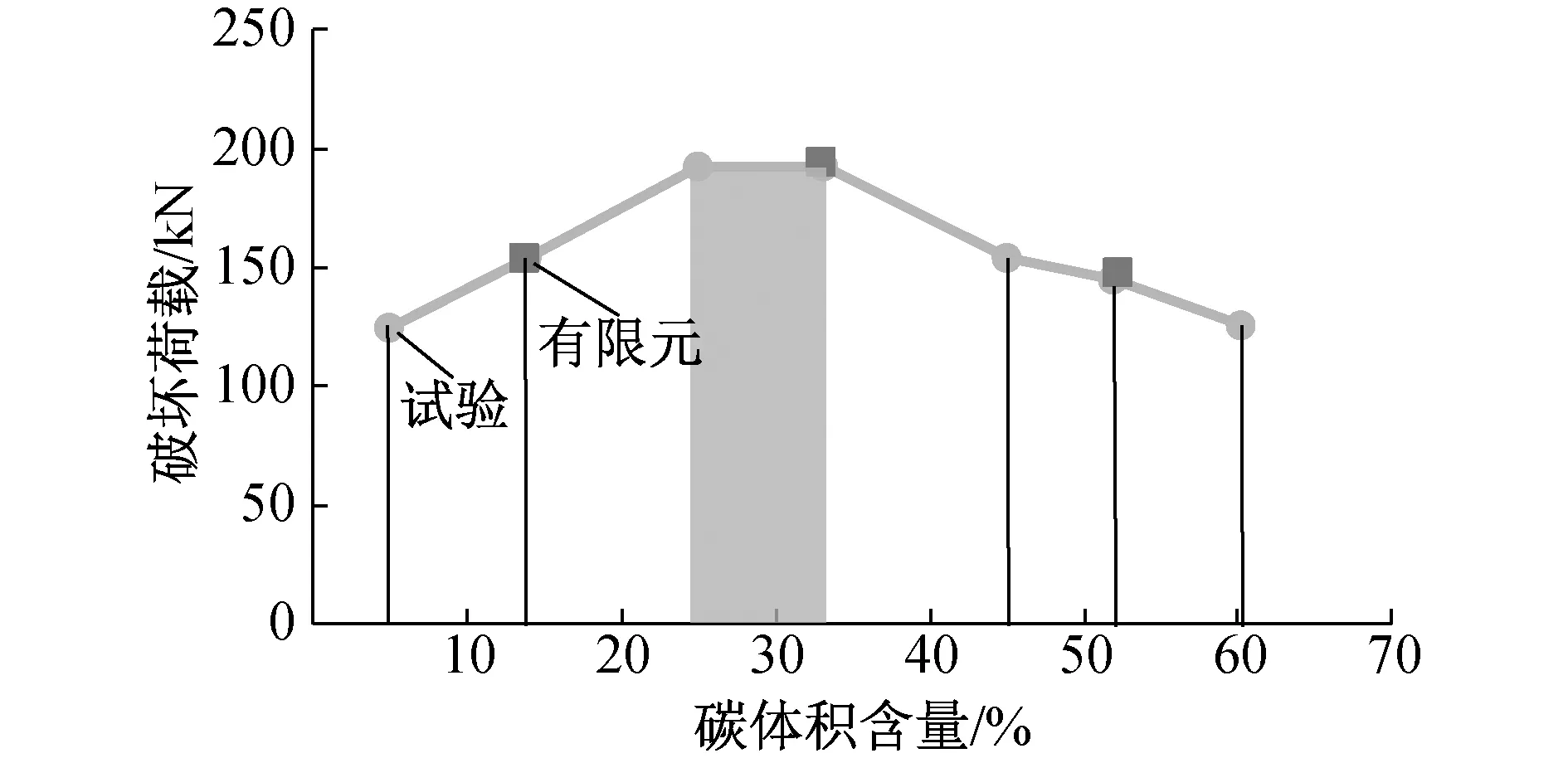
图13 翼缘碳体积含量与破坏荷载间关系

4 结语

1) FRP-i组合梁的翼缘与腹板宽度之比(bf/bw)对结构性能具有重要影响。NF梁(bf/bw=0.43)在弯矩作用下表现出稳定的线性行为，界面层受压翼缘脱层破坏为脆性破坏。WF梁(bf/bw=1.13)在屈曲和后屈曲区表现出不稳定的非线性行为，导致受压翼缘的脱层破坏。

2) FRP梁的破坏强度和破坏模式取决于翼缘碳含量。结果表明，碳含量越高，脱层程度越大，梁的破坏荷载越小。通过试验和数值计算，确定FRP梁翼缘最佳碳体积含量为25%～33%。

3)有限元分析与试验结果吻合较好，试验与有限元分析的平均破坏荷载差异<2%，并且2种方法得出的破坏模式相同，因此有限元分析可准确计算和设计混合FRP梁的强度。