升船机双塑性钢梁防撞装置设计研究

金 辽，廖乐康，王 可，胡吉祥

(长江水利委员会长江勘测规划设计研究有限责任公司，湖北 武汉 430010)

防撞装置是平衡重式升船机安全保障体系设计的重要设备之一[1-2]，本文提出了双塑性钢梁船舶失速拦防装置及其相关的分析和设计方法，该系统一方面通过两根塑性梁的前后布置，形成了对于失速船舶的冗余拦防，即使一根梁完全断裂，剩下的一根仍然具有设计拦防能力，增强了拦防的安全性；同时当一根防撞梁撞击受损，系统可继续工作直至升船机机中检修，解决了单根塑性梁受损更换影响升船机正常通航运行的问题。在单根塑性梁的设计公式推导方面，应力应变关系依然采用幂律本构关系，本构关系表达式根据钢材的试验应力应变关系构筑；塑性变形能的计算采用塑性应变比能在防撞钢梁全实体范围内积分的方法，物理概念更加严谨明确；同时利用泰勒公式和变量变换对相关表达式进行简化，使设计公式简洁明了，便于设计者应用。

1 工作原理

该防撞系统采用两级防撞梁前后布置的方式，形成对于失速船舶的两级拦防。防撞梁采用塑性设计钢梁，利用钢梁的塑性变形能吸收失速船舶的动能[3-4]。每一级防撞梁均具有单独吸收船舶全部动能的能力。当船舶失速时，与两级防撞梁的撞击梁碰撞，从而使撞击梁产生塑性变形。撞击梁和安全梁的布置间距保证撞击梁产生足够的塑性变形以便完全吸收船舶按设计速度行驶的动能；安全梁则形成船厢门保护的安全冗余，即使撞击梁被失速船舶撞损甚至丧失拦截功能，安全梁仍然以同样的能力通过塑性变形继续吸收剩余的船舶动能。与单塑性钢梁比较，由于采用双塑性梁方案产生了较大的安全冗余，因此可降低单根梁的截面尺寸，从而有效降低船舶与塑性梁的碰撞力，降低船舶撞击防撞梁的撞击载荷对船厢结构的不利影响(见图1、图2)。

图1 双塑性钢梁防撞装置布置图

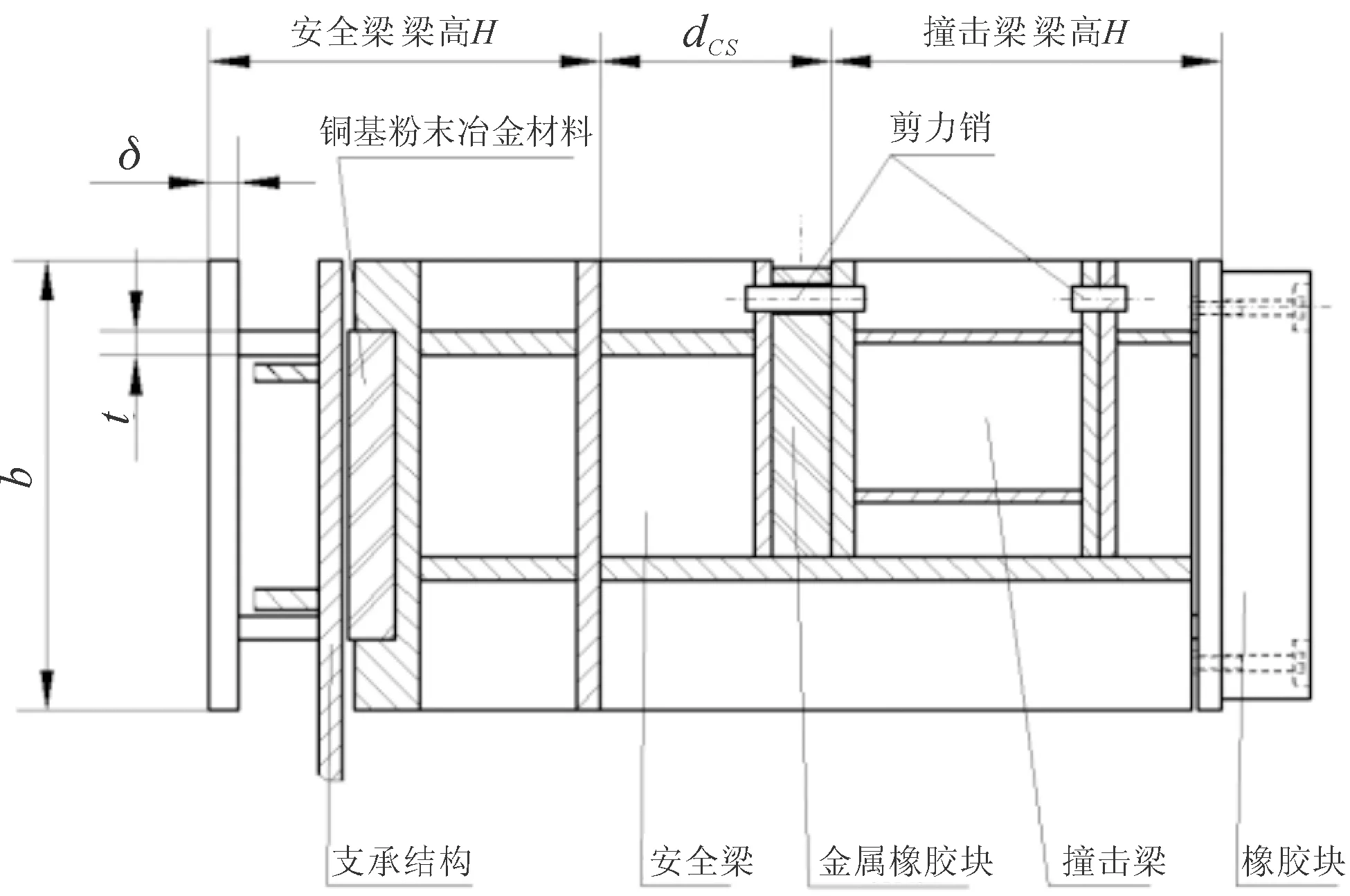
图2 双塑性钢梁防撞装置端部剖视图

2 双梁拦防系统的设计方法

2.1 塑性钢梁的吸能原理

如上所述，本文提出的双塑性钢梁船舶失速拦防技术的一个基本原则是每一根防撞梁均具有单独吸收船舶全部动能的能力。因此，对于单根塑性钢梁的设计方法的建立是该技术实施的基本前提。防撞梁和安全梁采用箱形断面。两根梁的主体断面相同，仅在端部结构上有所区别，因此为叙述方便，此处仅以防撞梁为例进行说明。为便于分析，防撞梁的计算模型假定为两端简支，在中间断面承受船舶撞击力P。

由于考虑利用钢梁的塑性变形吸收船舶动能，因此钢梁材料应力应变关系采用幂函数本构关系。幂函数弹塑性本构关系的形式为[5-6]：

σ=Aεn

(1)

式中：σ为应力；ε为应变；A、n为表征材料性质的常数，其值可通过所采用材料实际应力应变曲线的某些特征点来确定。

图3为钢材Q355D的材料应力应变关系曲线。红色曲线为Q355钢实测应力应变曲线[7]。根据该文献资料提取的两组数据，求得Q355的幂律本构关系参数为：n=0.21；A=873.7 N/mm2。因此其对应的幂律本构关系为

σ=873.7ε0.21

(2)

其本构关系曲线如图3中的蓝色曲线。从图3可以看出，采用幂律本构关系的塑性应变比能小于试验应力应变关系下的塑性应变比能。因此本文采用幂律本构关系推导的设计公式在防撞梁的强度计算方面是偏于安全的。

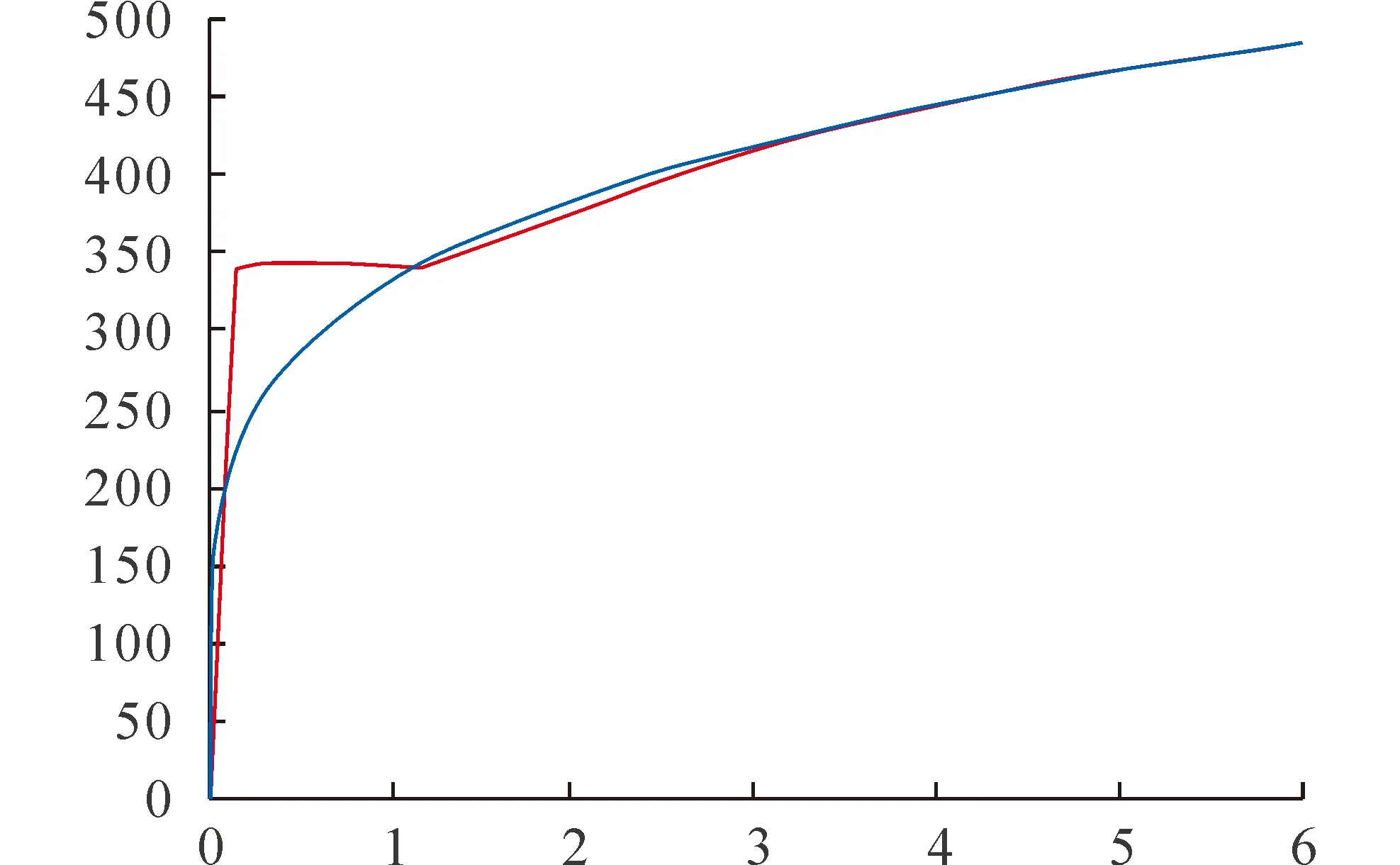
图3 Q355的应力应变关系试验曲线和幂率本构关系曲线

箱形断面为双腹板焊接件，其中上、下翼缘尺寸相同。截面参数：b为翼缘高度；δ为翼缘厚度；h为腹板高度；t为腹板厚度。

由于防撞梁的挠度相对于梁跨度较小，为便于分析，假定防撞梁满足小变形假设，此时，中心性轴长度不发生改变。假定防撞梁在x处曲率半径为R(x)，在该处取微段dx，可以求得处在距中性轴y处的梁纤维的应变为

(3)

式中：κ(x)=1/R(x)为梁的中性轴曲率；θ为微段dx与曲率对应的转角。将式(3)代入式(1)，得

σ=Aκ(x)nzn

(4)

截面弯矩为

(5)

根据泰勒展开公式，当h≪x时

式中，Rn为余项。

将上式中的f(x)以(x/2)n+2代之，可得

(6)

将式(6)代入式(5)，可得

M(x)=Dκ(x)n

(7)

式中：

(8)

令

(9)

则

(10)

式中，Sd为箱形梁的折算面积。

对于塑性防撞梁，由于是按设计船型的载重量来确定撞击质量的[8]，而设计船型的宽度只是略小于船厢有效宽度。因此可合理地假定撞击力作用在中间断面。由于防撞梁为两端简支，因此，当x≤L/2，其截面弯矩亦为

(11)

式中，P为船舶与防撞梁之间的撞击力。

将式(7)代入式(11)，可求得

(12)

将式(12)代入式(3)，得

(13)

防撞梁的塑性应变能为应变能密度在梁整个体积V内的积分

(14)

考虑结构的对称性，防撞梁的塑性应变能为

(15)

假设设计船舶(最大排水量)以设计允许的最大速度撞击防撞梁，则防撞梁与防撞梁之间产生最大撞击力Pmax，在其中断面(x=L/2)的最外侧(z=H/2)产生最大应力或最大应变。假设该应变为εmax，则根据式(13)，最大应变为

(16)

根据式(16)可求出最大撞击力为

(17)

将式(17)表示的Pmax值取代式(15)中的撞击力P，则求得防撞梁的最大应变能为

(18)

根据式(10)

(19)

式中，ξ=h/H为箱形梁腹板高度与梁高之比。

将式(19)代入式(18)，得

(20)

假定船舶失速的动能全部转化为防撞梁弹塑性应变能，即Tmax=Wmax，则根据式(20)

(21)

则防撞梁最大应变为

(22)

式(17)碰撞力可作如下改变

(23)

根据防撞梁的小变形假设，由式(12)

(24)

式(24)对x积分，可求得

(25)

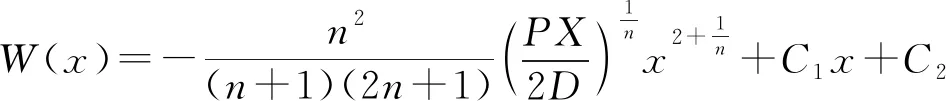
防撞梁为受对称载荷简支梁，其边界条件为中部转角为零和端部挠度为零。根据中部转角为零条件，求得

(27)

根据端部挠度为零条件，求得

C2=0

(28)

将式(27)和式(28)代入式(26)，求得

(29)

梁的最大挠度发生在中部，将x=L/2，P=Pmax代入式(29)，求得撞击梁最大挠度为

(30)

根据式(17)

(31)

将式(31)代入式(30)，得

(32)

2.2 计算实例

以三峡升船机为例进行计算。设计船型最大排水量(亦即船舶总质量)为ms=3 000 t，船舶在船厢行驶速度为0.5 m/s。防撞梁支承间距为L=18 m。

塑性钢梁采用Q355材料，并采用如图3所示的箱型断面，其尺寸为H=660 mm，h=560 mm，t=40 mm，δ=50 mm，b=760 mm，ξ=0.848 5。根据式(9)，求得Sd=96 271.5 mm2。将Q355的材料数据代入，并考虑物理量的量纲和船舶及其附连水体总质量按2倍的设计船舶总质量确定[9-10]，根据式(22)，得

式中，[ε]为最大允许发生塑性应变。

根据文献[7]给出的Q355钢工程应力应变全范围曲线，该钢材在断裂时的塑性应变达到60%。为保证钢梁不发生断裂破坏，最大允许发生塑性应变应远小于钢材强度极限所对应的塑性应变。本文推荐最大允许发生塑性应变不超过2%。

根据式(23)

式中，[P]为许用碰撞力。

将该载荷值平均分配至防撞梁的两端，用以计算双塑性钢梁组的支承构件与船厢主纵梁内腹板的连接焊缝。考虑4条长度为400 mm、高度为24 mm的剪切焊缝，并考虑1.5的应力分布不均，求得焊缝剪应力为53.8 N/mm2。说明碰撞力满足要求。

根据式(32)

取撞击梁和安全梁的最小间距为390 mm。按照该设计布置的双塑性钢梁防撞装置满足三峡升船机厢头布置和船厢有效长度要求。

3 结 语

1)本文针对现有单塑性梁防撞系统需在撞击后即时更换从而影响升船机通航的缺点，提出了双塑性钢梁冗余拦防的船舶失速防撞系统设计概念，阐述了该系统的设备布置和工作原理，并提出了该系统的设计控制条件。

2)在塑性钢梁吸能原理计算方面，利用幂律塑性本构关系，采用塑性应变比能在塑性钢梁全体积域内积分的方法计算钢梁塑性应变能，并通过动能与钢梁塑性应变能相等的原则，推导了单根塑性钢梁的设计计算公式。同时利用泰勒公式和变量变换对相关表达式进行简化，使设计公式简洁明了，便于设计者应用。

3)通过对三峡升船机防撞系统的实例计算，说明双塑性钢梁冗余拦防在升船机的应用具有可行性，可供升船机设计人员参考。