基于能量峰定位的经验小波变换及在轴承微弱故障诊断中的应用

张西宁,李霖,刘书语,雷建庚

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)

滚动轴承作为广泛使用的基础零部件,是旋转机械的关键支撑部件[1-2]。滚动轴承易于损坏,且寿命的分散性大,机械故障中21%是由滚动轴承损坏引起的[3]。一旦轴承出现事故,将导致整台设备停机,由此带来巨大的经济损失[4]。因此,开展轴承故障诊断方法研究具有重要的理论意义和应用价值。

时频分析可以同时展示信号在时域和频域的信息,是提取非平稳信号特征的有效工具。各种时频分析方法被广泛应用于轴承故障诊断[5],如短时傅里叶变换(STFT)[6]、Wigner-Ville分布(WVD)[7]、小波变换[8]、经验模态分解(EMD)[9-10]等,但存在各自的缺陷。STFT采用固定窗口,时频分辨率有限[11];WVD存在交叉项干扰[12];小波变换需要挑选合适的小波基函数;EMD能够自适应地分离信号中的分量,但缺乏数学理论,存在模态混叠和端点效应[13]。

针对EMD的不足,Gilles提出了经验小波变换(EWT)方法,该方法结合了EMD的自适应特性和小波分析的理论框架[14]。其核心思想是对频谱进行恰当分割,通过设计合适的小波滤波器组来提取信号的不同模态。

EWT方法提出以来,在机械故障诊断领域得到了广泛应用。陈景龙等将EWT方法用于风力发电机中轴承故障诊断[15],取得了良好效果。王友仁等提出能量聚集度EWT方法,成功实现了齿轮箱早期故障诊断[14]。祝文颖针对EWT分解对噪声敏感的问题,提出了一种单分量个数的估算方法,为经验小波变换中的Fourier频谱划分提供了一种解决思路[16]。Hu采用基于阶统计滤波器的包络方法对分割算法进行改进,但是作者没有确定选择最佳包络函数的准则[17]。邓飞跃等随后引入一个带宽可变的滑动频率窗口,自适应确定滑动频率窗口位置,使得信号频谱分割更为准确[18],但需要付出大的计算代价。

对EWT方法研究现状进行分析,不难得出其存在以下问题:①EWT方法是根据快速傅里叶变换(FFT)谱局部极大值点确定频谱分割边界的,而FFT谱易受噪声和非平稳因素的干扰出现“伪”局部极大值,分割边界错误直接导致EWT分解失败,可见频谱分割是EWT的关键;②基于包络或平滑的改进方法最优参数确定困难,分割效果参差不一,原因是单纯依赖一次包络或平滑结果便确定频谱分割边界显得过于武断,一旦包络或平滑参数设置错误,将直接导致EWT分解失败,有“一叶障目不见泰山”之感。

针对以上问题,本文提出了一种多尺度能量峰定位经验小波变换(EPL-EWT)方法。该方法首先从频谱能量角度出发,对频谱进行能量集中,降低噪声的影响。其次,提出一种多尺度寻峰定位算法,从原始EWT依赖“局部最大值点”转变为根据“能量峰位置”确定分割边界,从整体上考虑了频谱几何形状,可以自适应地确定频谱分割边界,快速、准确地提取并增强轴承故障特征。

1 理论基础

1.1 经验小波变换

EWT包括两个重要步骤:

(1)确定信号频谱分割边界;

(2)经验小波滤波器组的建立及模态提取。

考虑一个归一化的周期为2π的Fourier轴,为了符合Shannon采样定理,频率被限制在ω∈[0,π]。假设将Fourier支撑[0,π]分割为N个连续的子带,用ωn表示每个子带的边界(其中ω0=0,ωN=π),如图1所示。

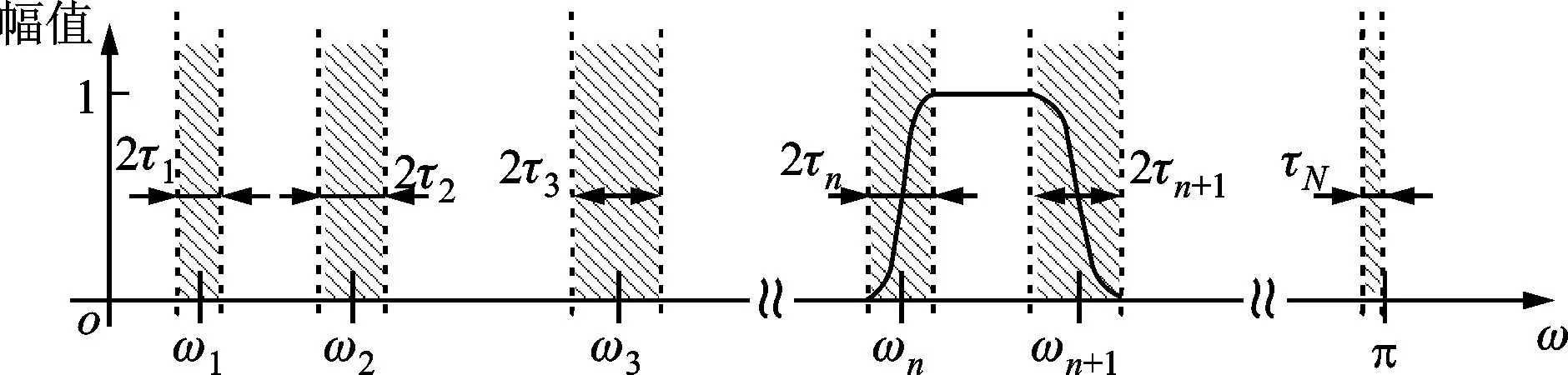
图1 傅里叶轴的分割示意图[11]Fig.1 Segmentation of Fourier axis

(1)

(2)

(3)

近似系数由信号和尺度函数的内积得到

(4)

式中:φ1为尺度函数。

原信号的重构为

(5)

根据这种形式,信号f的经验模态可以定义为

(6)

(7)

1.2 Tearger能量算子

Teager能量算子最早是在1980年由Teager提出,用于表征声音信号能量大小的一种方法。对于任意连续信号x(t),Teager能量算子Ψ定义为

(8)

Ψ(x(n))=[x(n)]2-x(n-1)x(n+1)

(9)

2 改进的经验小波变换EPL-EWT

轴承发生故障时,缺陷位置的瞬时碰撞会激起轴承固有频率发生共振,在频谱上表现为一个个“谱峰”,且固有频率会充当载波被轴承故障频率调制。从包络解调角度来看,每个谱峰对应的信号可以认为是一个固有模态,对这些模态做包络分析,可以充分暴露轴承故障特征。因此,本文提出了一种能量峰定位的经验小波变换(EPL-EWT)方法。首先利用Teager能量算子对傅里叶频谱进行谱能量集中,降低噪声和无关分量的影响。然后采用多尺度寻峰定位算法,准确识别能量谱中“峰”的位置,相邻峰位置的中点被确定谱分割边界,最后建立经验小波滤波器组,提取各个模态分量。方法的具体步骤如下。

(1)Teager能量算子频谱能量集中。傅里叶频谱对噪声比较敏感,极易出现伪“局部极大值点”。白噪声虽然会影响频谱中单个点的幅值,但其能量在整个频域上是均匀分布的。利用Teager能量算子,对频谱进行能量集中,有

(10)

从谱能量角度确定谱分割边界比单纯从幅值角度更为可靠,在很大程度上减少了噪声对分割的干扰。

对于给定N×1维输入序列v,定义峰值判别准则C,C是一个N×1维向量,初始化为0。

(Ⅰ)检测v中所有局部极大值点,组成集合P,并对C作第一次更新,令

∀p∈P,C(p)←v(p)

(11)

第一次更新C时使用v(p)的基本原理是,促进v中具有较大振幅的点作为峰值。将每次检测到的峰值存储在集合O中,即

O←P

(12)

(Ⅱ)使用S个不同宽度尺度si对信号v进行S次平滑,得到对应的平滑版本vi

vi=W(si)*v

(13)

式中:si=iN/(20s),i=1,2,…,S;W(si)表示标准化的高斯窗函数。

每次平滑后重新检测局部极大值,得到新的集合Pi,将新的局部极大值与之前O中的点相关联,并增加其C值,因为在不同的尺度下它们被多次挑选出来,表明它们确实是一个是“峰”。通过确定旧集合O中哪些元素最接近P的每个元素,从而建立P元素邻近的集合I

(14)

当识别出I后,增加相应的判据C,这里我们设定ΔC既依赖于信号值,又依赖于尺度s

∀p∈P,ΔC(I(p))=v(I(p))s2

(15)

使用s2目的是:在连续的平滑过程中显著突出保持峰值的点。此外,增加I的元素而不是增加P的元素是为了避免在每次迭代中增加不同点的C值,因为在不同的平滑尺度下局部极大值之间会发生漂移。

(Ⅲ)进行完S次尺度迭代后,根据C确定“目标峰”位置。若给定峰检测数目N,取C值最大的前N个点;若给定阈值ρ∈(0,1),则C>ρmax(C)。

(3)将挑选出来的相邻峰位置的中点作为经验小波谱分割边界,建立相应的经验小波滤波器组,提取相应模态分量。

(4)计算各分量的峭度指标值,选择峭度指标值最大的分量进行包络分析,诊断轴承故障类型。

提出的EPL-EWT方法流程如图2所示。

3 仿真信号分析

为了验证本文方法的优越性,以外圈故障为例,建立了一组脉冲信号来模拟故障轴承的振动信号。仿真信号如下

x(t)=e-αt′(0.4sin(2πf1t)+sin(2πf2t)+

1.5sin(2πf3t))

t′=mod(t,1/fm)

式中:α=800为衰减指数;fm=100为调制频率;f1=900 Hz、f2=2 500 Hz与f3=4 000 Hz表示载波频率,运算mod(a,m)返回a除以m后的余数。因此,模拟的滚动轴承故障频率为100 Hz,固有频率为900、2 500和4 000 Hz。采样频率为10 240 Hz。在信号中加入信噪比为-15 dB的高斯白噪声,模拟滚动轴承实际工作环境中的背景噪声和干扰信号,仿真信号时域波形图和频谱图如图2、图3所示。

图3 仿真信号时域波形Fig.3 Time domain waveform of simulation signal

图4 仿真信号频谱图Fig.4 Spectrum of simulation signal

对信号进行了基于原始EWT和改进的EPL-EWT分解,图5和图6为相应分割结果。

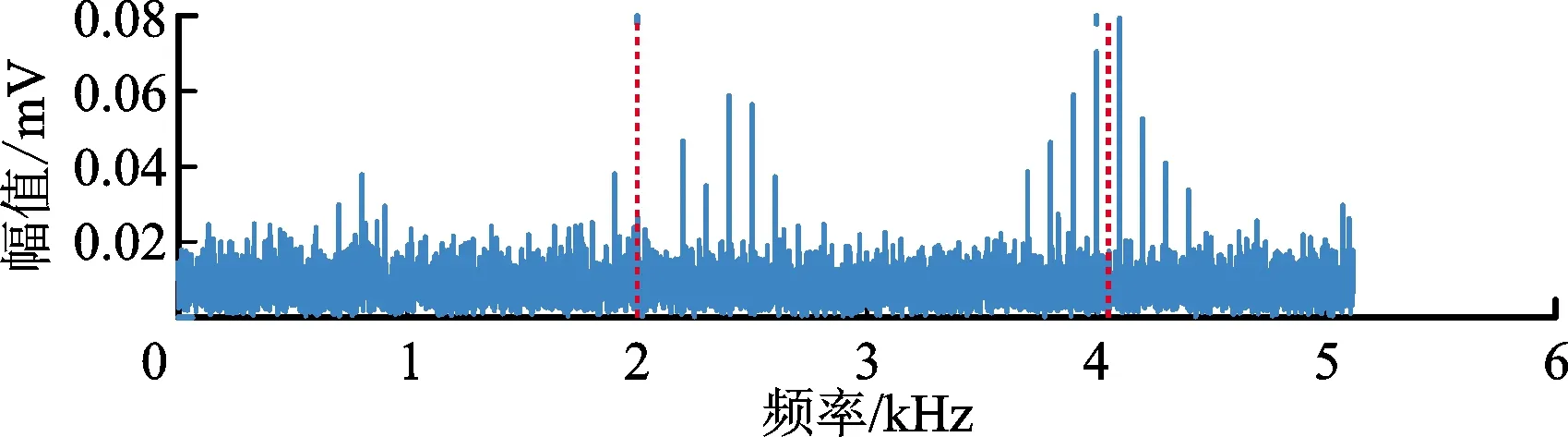
图5 原始EWT频谱分割结果Fig.5 Spectrum segmentation results of original EWT

图6 EPL-EWT频谱分割结果Fig.6 Spectrum segmentation results of EPL-EWT

对比图5、图6可以看出,采用原始EWT方法得到的分割效果并不理想。以第3个固有频率900 Hz为中心的模态检测过宽;以固有频率3 000 Hz为中心的模态虽然被检测出来,但左侧边界检测偏大;以固有频率为4 000 Hz的模态则完全分割错误,本来是一个完整共振频带被强行分成了两半。改进后的EPL-EWT方法能很好地检测出3个固有频率激起的共振频带,避免了原始EWT不当分割导致的频带破裂现象,故障信息保存完好。这种分解对于后续的包络解调分析十分关键,有利于故障特征的提取。改进前后的方法包络结果比较如图7和图8所示。为验证方法的有效性,定义轴承微弱故障特征显著性指标[21]为

(16)

图7 原始EWT挑选模态包络谱Fig.7 The original EWT selected mode envelope spectrum

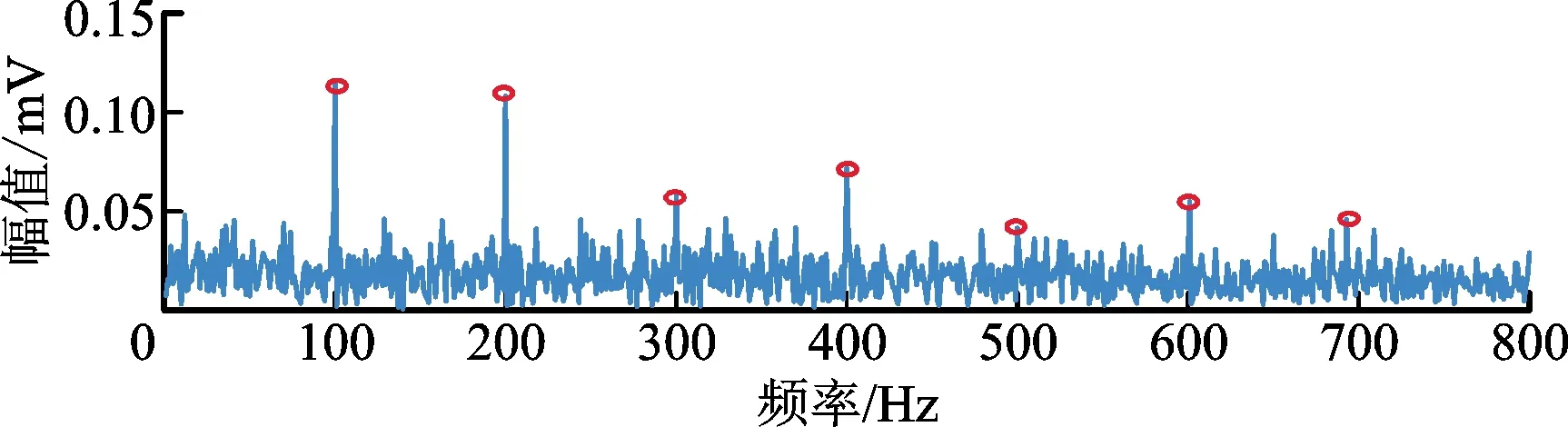
图8 EPL-EWT挑选模态包络谱Fig.8 EPL-EWT selected mode envelope spectrum

通过计算,原始EWT方法的Ibfc为0.010 237,改进后的EPL-EWT方法的Ibfc为0.046 239,改进后性能比原来提升了3.52倍。仿真结果说明,改进后的方法在提取轴承微弱故障特征方面具有较好的效果。

4 实验验证

为进一步验证EPL-EWT方法的有效性,开展了滚动轴承故障诊断实验。实验轴承类型为6308深沟球轴承,选取微弱故障轴承,局部故障通过激光在外圈和内圈的滚道表面中间及滚动体表面分别加工了直径为0.5 mm、深度为0.1 mm的凹坑。实验台如图9所示,所用传感器为IMI601A11加速度计,信号采样频率为10 240 Hz,采样持续1 s。轴承内圈实验转速约为1 200 r/min,外圈、内圈、滚动体故障特征频率分别为62.5、98.0、82.8 Hz。因外圈故障较容易识别,下面仅给出轴承内圈和滚动体微弱故障振动信号处理的结果。

图9 滚动轴承实验台Fig.9 Rolling bearing test bench

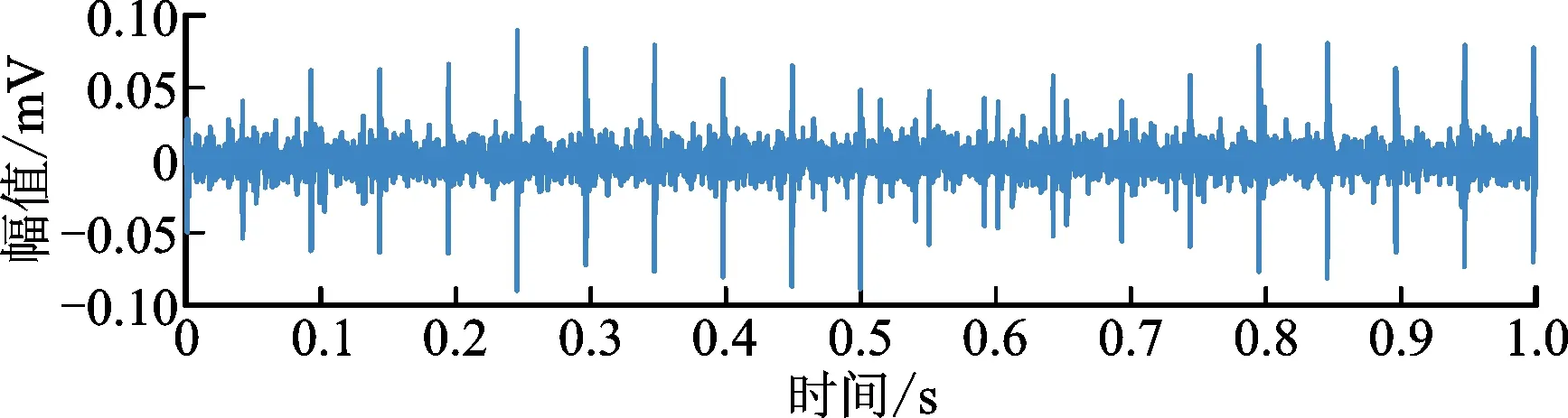
图10 内圈故障振动信号Fig.10 Inner ring fault vibration signals

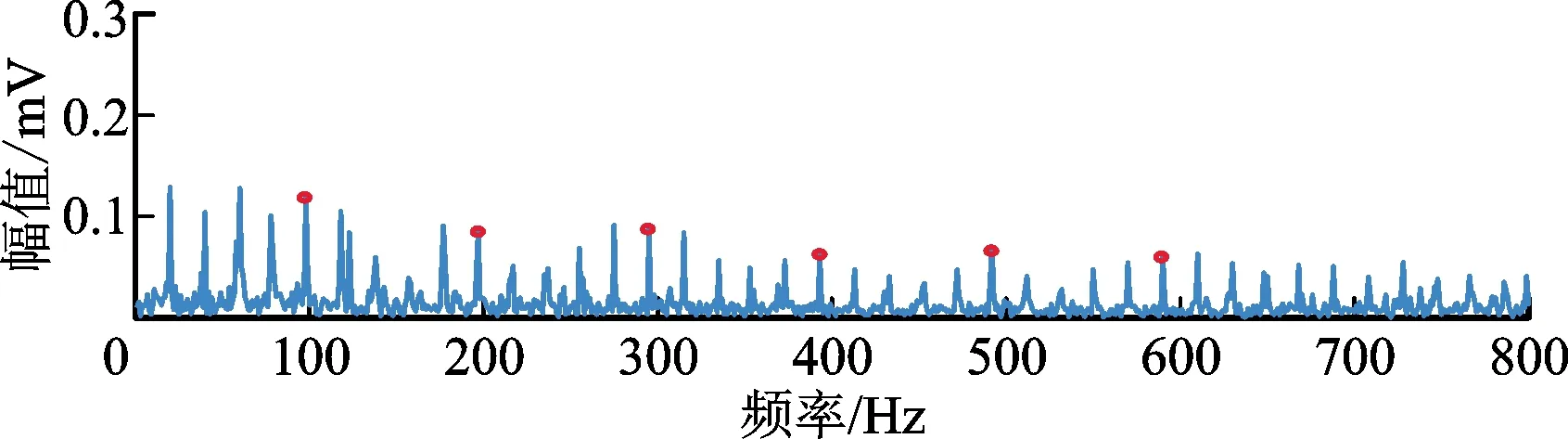
图11 内圈振动信号包络谱Fig.11 Envelope spectrum of inner ring vibration signal

原始信号时域波形和包络谱如图10、图11所示。从原始信号包络谱中虽然可以勉强找到内圈故障频率及其个别倍频,但幅值不明显,被转频及其他频率成分所淹没,很难充分判断发生了内圈故障。将内圈信号分别用原始EWT方法和改进的EPL-EWT方法处理,挑选峭度指标值最大的模态进行包络分析,结果如图12～图17所示。

图12 内圈故障振动信号原始EWT频谱分割结果Fig.12 Original EWT spectrum segmentation results of inner ring fault vibration signals

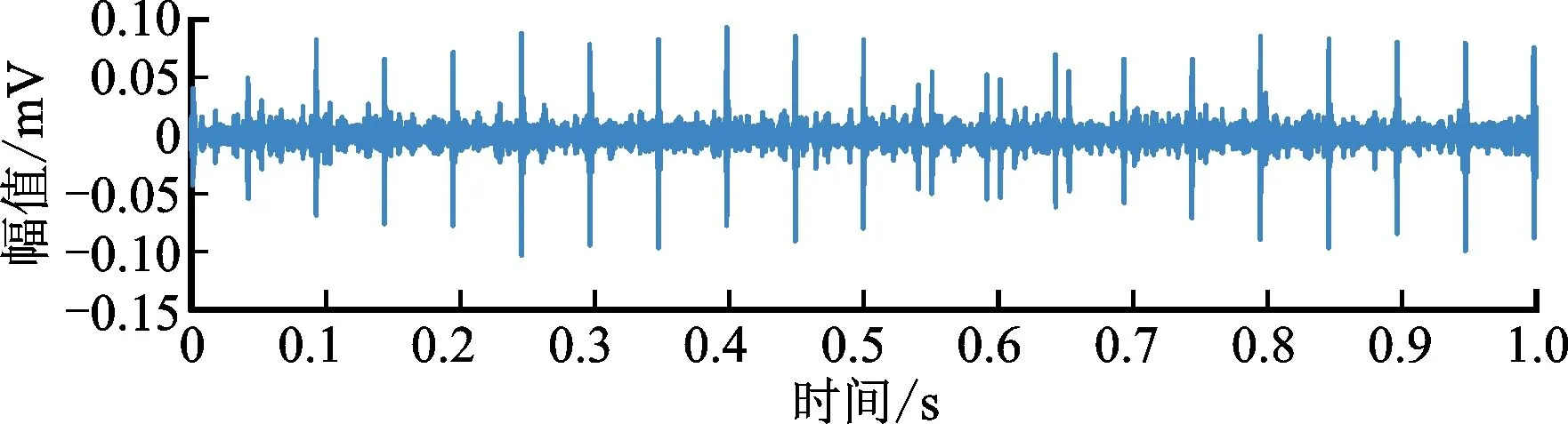
图13 原始EWT分解后峭度指标最大模态时域波形Fig.13 Time domain waveform of maximal kurtosis index mode after original EWT decomposition

图14 原始EWT挑选模态包络谱Fig.14 Original EWT selected mode envelope spectrum

从处理结果可以看出,原始EWT分割主要集中在低频段,不仅没有成功检测出共振频带,而且完整故障频带被错误分裂开。以至经EWT分解后,Hilbert包络谱(见图14)原始信号包络谱(见图11)相比效果提升不大。这反映了原始EWT方法依赖频谱局部极大值点确定分割边界的缺陷,受噪声和无关分量产生的伪值影响,原始EWT方法在轴承故障诊断中显得能力有限。

应用改进后的EPL-EWT方法,对轴承内圈微弱故障振动信号处理结果如图15～图17所示。

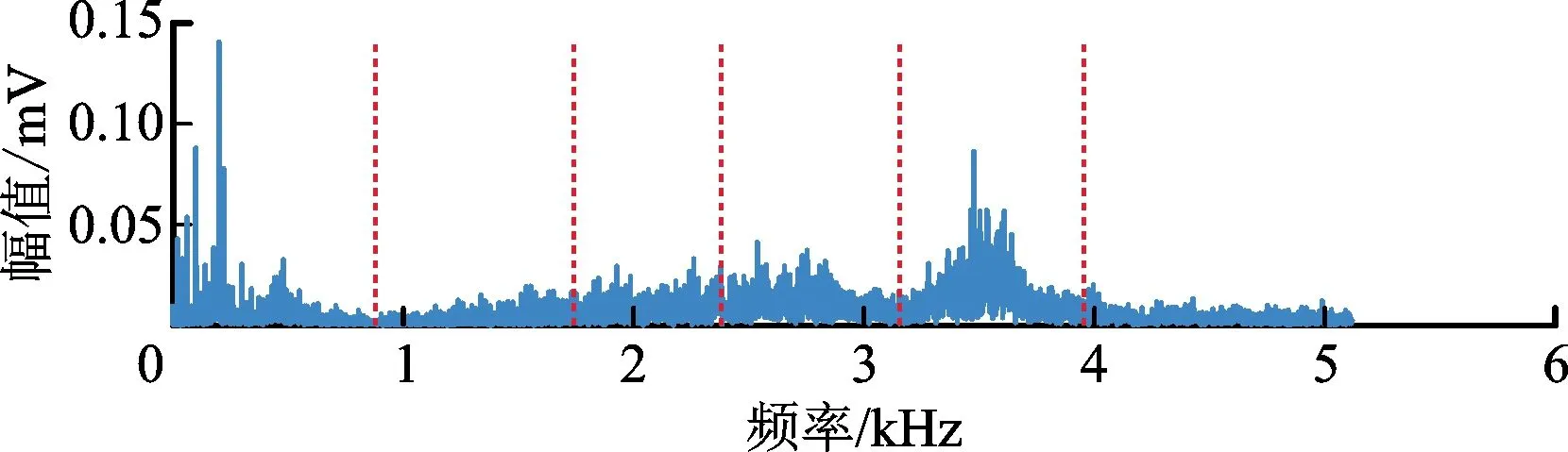
图15 内圈故障振动信号EPL-EWT频谱分割结果Fig.15 Results of EPL-EWT spectrum segmentation of inner ring fault vibration signals

图16 EPL-EWT分解后峭度指标最大模态时域波形Fig.16 Maximum modal time domain waveform of kurtosis index after EPL-EWT decomposition

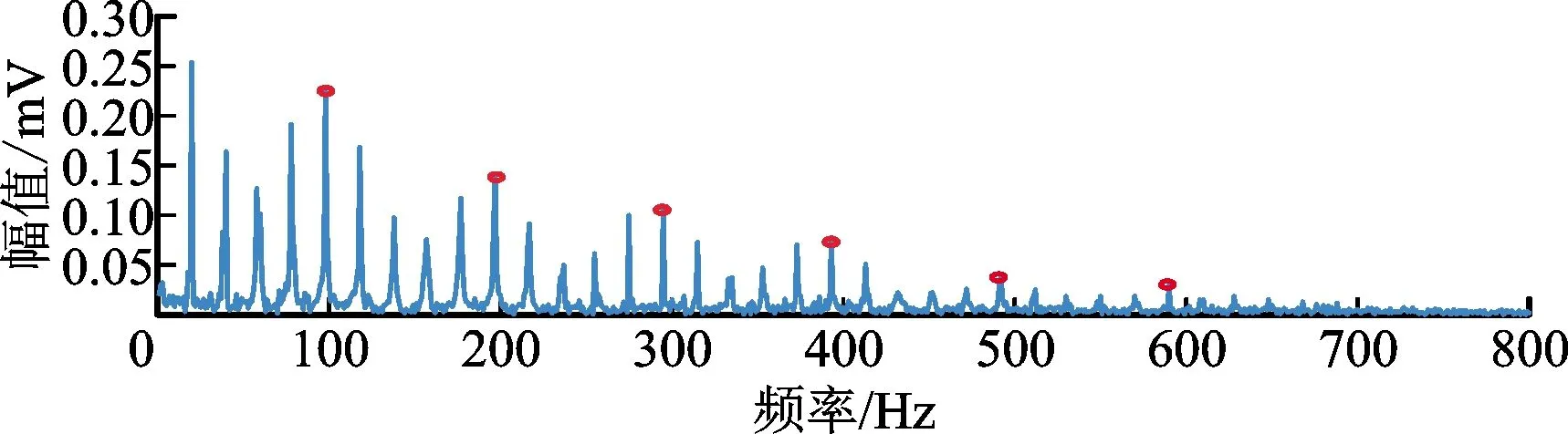
图17 EPL-EWT挑选模态包络谱Fig.17 EPL-EWT selected mode envelope spectrum

对比原始EWT方法,改进后的EPL-EWT方法频谱分割考虑到了频谱形状,成功检测出了轴承共振频带,分割更恰当。包络谱故障频率及倍频更明显,故障特征得到了增强。分别对改进前后的方法进行特征显著性指标计算,原始EWT方法的Ifea为0.213 92,改进后的EPL-EWT方法的Ifea为0.326 22,改进后性能比原来提升了52.50%。这得益于EPL-EWT方法从能量角度入手,提高了对噪声的鲁棒性,利用多尺度寻峰定位算法使得边界检测更加准确,能自适应地识别故障共振频带。包络分析结果证明分解的模态更加符合轴承振动物理意义。

对轴承滚动体微弱故障振动信号进行分析,原始信号时域波形与包络谱如图18、图19所示。

图18 滚动体故障振动信号Fig.18 Vibration signal of rolling element fault

图19 滚动体故障振动信号包络谱Fig.19 Envelope spectrum of vibration signal of rolling element fault

从滚动体微弱故障轴承原始信号的包络谱中看到的故障频率倍频有限,勉强可以找到一倍频,但幅值很低,若事先不知轴承故障类型,单靠以上信息很难妄下结论。这是由于包络分析需要选择合适的频带,单纯的直接对原始信号进行包络分析在微弱故障面前显得力不从心。对轴承振动信号应用原始EWT方法,分析结果如图20～图22所示。

图20 滚动体故障振动信号原始EWT频谱分割结果Fig.20 Original EWT spectrum segmentation results of vibration signal of rolling element fault

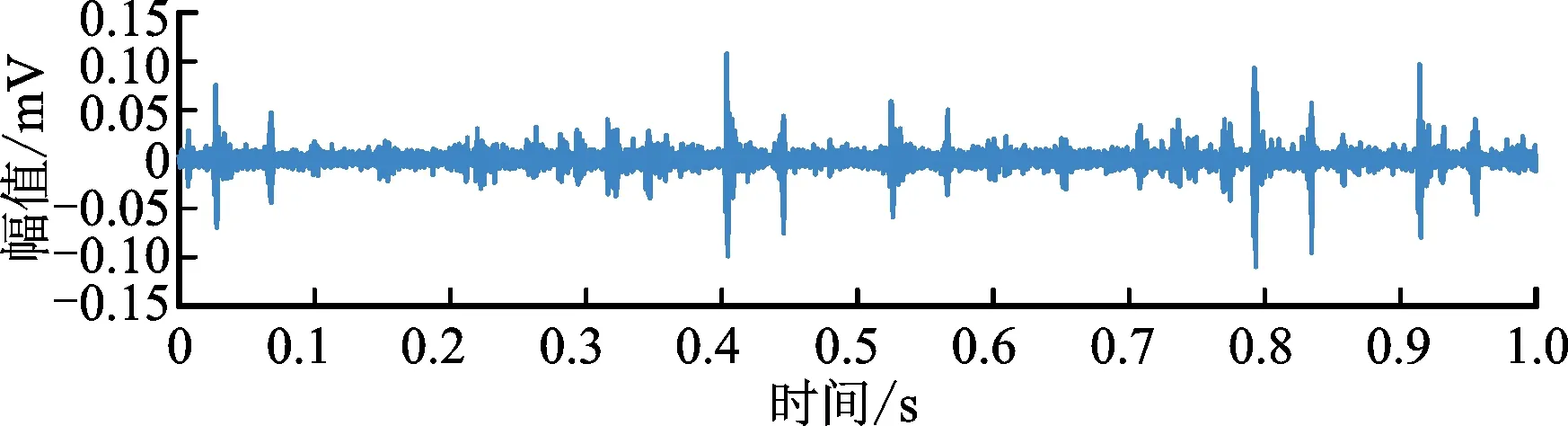
图21 原始EWT分解后峭度指标最大模态时域波形Fig.21 Maximum modal time domain waveform of kurtosis index after original EWT decomposition

图22 原始EWT挑选模态包络谱Fig.22 Original EWT selected modal envelope spectrum

显然,原始EWT方法出现分割不均、局部频带分割过细的现象,共振频带的检测以失败告终,挑选模态的包络谱中故障频率被其他成分所淹没。这是由于受噪声和无关分量影响导致频谱上低频部分同时出现多个“局部极大值点”,故原始EWT方法根据局部极大值点会在低频区确定多个相邻很近的分割边界。边界检测一旦出现错误,EWT分解必然失败,原始EWT方法缺陷暴露无疑。

对轴承滚动体微弱故障振动信号应用改进后的EPL-EWT方法,处理结果如图23～图25所示。

图23 滚动体故障振动信号EPL-EWT方法分割结果Fig.23 Spectrum segmentation results of EPL-EWT for vibration signals of rolling element fault

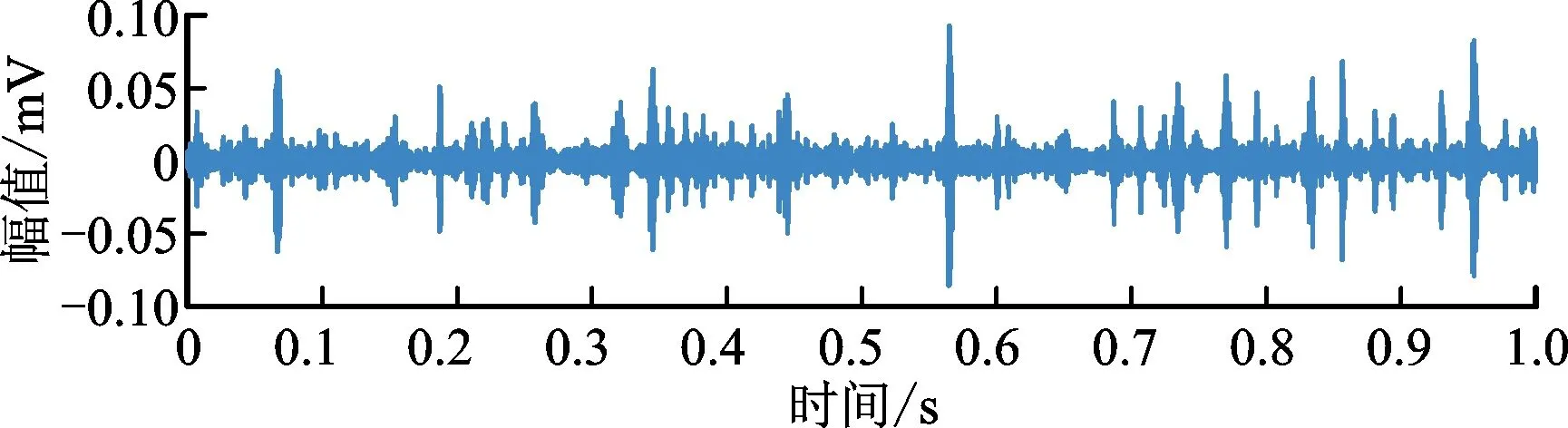
图24 EPL-EWT方法分解后峭度指标最大模态时域波形Fig.24 Time domain waveform of maximum mode kurtosis index after EPL-EWT decomposition

图25 EPL-EWT方法挑选模态包络谱Fig.25 EPL-EWT selected mode envelope spectrum

对比原始EWT方法结果,改进后的EPL-EWT方法自适应地检测到了轴承滚动体微弱故障的共振频带,频谱分割恰当,保留了完整的故障频带,有利于故障信息的集中。从包络谱可以看出,改进后的方法故障特征显著提升,故障频率一倍频幅值提高近30%,对原始EWT和改进EPL-EWT方法进行特征显著性指标计算,原始EWT方法的Ifea为0.013 144,改进后的EPL-EWT方法的Ifea为0.019 180,改进后性能比原来提升了45.92%,证明了所提方法的有效性。

5 结 论

本文针对原始EWT方法对噪声敏感、模态分解不当的问题,从频谱能量角度入手,利用多尺度寻峰定位提出一种自适应能量峰定位的EPL-EWT方法。在滚动轴承故障诊断实验中,本文方法与原始EWT方法相比,鲁棒性更强,故障特征更明显,诊断更准确。

(1)利用Teager能量算子对频谱进行谱能量集中,大大减少了噪声和无关分量对频谱分割的错误影响,提高了方法的鲁棒性。

(2)提出的EPL-EWT方法,可以自适应地检测分割边界,多尺度寻“峰”定位。与原始EWT依赖“局部极大值点”相比,避免了因单个“伪值点”造成的武断决策,使频谱分割更加恰当。

(3)改进的EPL-EWT方法考虑了频谱形状,可以自适应地准确识别故障轴承的共振频带,分解的模态符合轴承振动的物理意义。相比原始EWT方法,针对内圈微弱故障和滚动体微弱故障,改进后的EPL-EWT方法特征显著性指标分别提高了52.50%和45.92%,实现了特征增强,可用于轴承微弱故障诊断。