仿象鼻气动连续体机器人的运动学建模与运动控制
张启航,邵敏,任树雄,李源,王晶
(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学工程坊,710049,西安)
连续体机器人是一种新型仿生机器人,它模仿自然界中象鼻、章鱼臂等动物器官的运动机理,自身不存在离散关节,但能依靠连续柔性变形实现运动操作[1]。连续体机器人具有刚度小、柔性高的特点,在遇到外部障碍物时,能够改变自身形状适应外部环境。相比传统刚性杆件机器人,柔性机器人具有多项明显的优势,例如可以与环境实现安全交互、在受限空间内实现灵巧操作以及抓取非结构化物体等,因而在最近十余年成为了研究热点。
连续体机器人一般由低弹性模量的材料制成不具有可分辨的旋转关节,其形状由连续曲线表征,因此其精确位姿的获得是一个难点,这也导致了连续体机器人的控制存在一些困难[2-4]。研究人员提出了一些描述连续体机器人变形的方法,如基于Cosserat梁理论建立连续体运动学模型[5-6],该模型综合考虑了材料特性、负载和重力等因素,能够对连续体机器人的变形进行比较精确的描述。Ivanescu等通过分析章鱼的卷绕动作,提出了描述章鱼触手的卷绕物体的方程,并利用该方程对连续体机器人的动力学进行了研究[7]。Rucker等提出了一种精确几何模型用于描述同心管连续体的运动[8]。Anderson采用多段曲线的组合描述连续体机器人[9]。与此类似,也有研究人员采用样条曲线描述连续体机器人中心线[10-11]。Grazioso等认为连续体机器人的变形形成一些相互正切的螺旋线,利用微分几何和指数坐标为机器人的构型提供了直观有效的描述[12]。
上述模型大多涉及到高阶偏微分方程的求解以及材料力学知识,计算较为复杂,不利于对连续体进行实时控制,因此实际应用中并不多见。随着计算机技术的进步,研究人员提出利用机器学习的方法解决连续体机器人的运动控制难题[13]。Melingui和Merzouki将多层感知机和径向基网络引入到末端监督学习方案,求解RobotinoXT机器人的运动学[14]。Reinhart和Jochen采用单隐层线性回归网络学习连续体机器人的运动学[15]。谭宁等提出了一种零位调整神经动力方法,依靠机器人输入和传感器输出信息就可以实现对连续体的控制[16]。但是,这些模型却不能描述连续体的具体变形。由于连续体机构的结构特性,在无负载和小负载情况下,连续体构节变形接近于常曲率变形,故连续体机器人变形模型大多用常曲率圆弧表示[17-20]。大部分连续体机器人的运动学或动力学模型均是基于常曲率变形假设,该假设大大简化了描述构节变形的难度,使得机器人位姿的实时计算变得可行[21-23]。
本文采用常曲率模型,对一种自行研制的仿象鼻气动连续体机器人进行运动学建模,并用相应的实验,验证该模型对控制本气动连续体机器人运动的可行性。这项研究对于同类型连续体机器人的位姿控制具有重要的指导与借鉴意义。
1 机器人平台简介
本文以一种自行研制的仿象鼻气动连续体机器人作为研究对象,该机器人的结构如图1a所示。机器人由3个气动构节和一个气动抓手串联组成,每个构节由3个气动肌肉并联组成(120°均匀分布),如图1b所示。通过控制3个气动肌肉内气压的大小,便可使单个构节发生伸长或弯曲变形。3个构节组合在一起,可使该仿象鼻机器人实现复杂的变形运动。机器人的3个构节中间安装有间隔盘(数量为4,3,2),每个气动肌肉最外侧都安装有拉线传感器,用来分别监测9个气动肌肉的长度变化。
对于连续体机器人,运动学模型描述的是驱动器长度和机器人末端位姿之间的关系。仿象鼻气动连续体机器人的运动学模型如下
x=fD-H(f2(f1(l)))
(1)
式中:f1表示从拉线长度到构节变形参数的函数关系;f2表示构节变形参数转换为离散关节的函数关系;fD-H表示通过D-H方法建立的机器人齐次变换关系[24]。
2 机器人常曲率模型的建立
基于以下两个原因,做出“单个构节中心线上各部分曲率保持一致”的假设:①连续体机器人的设计通常都形成了一系列的连接截面;②每个截面内部势能均匀分布,构节内部的受力沿构节中心线均匀分布。本文气动肌肉构节符合这两个假设条件。
2.1 连续体构节变形模型
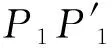

(a)构节变形模型

(b)某一小节弯曲内拉线关系示意图
(c)投影平面示意图
图2c中存在一个等腰三角形分别包含有r1和lc/n。G点为CC′的中点,k点为CC′与平面H的交点。通过拉线的空间位置关系可由h2、h3计算出hc,再通过三角形的相似原理,可得到到k1、k2和k3的表达式如下
(2)
(3)
(4)
3个拉线安装点和原点的连线与x轴的夹角分别为90°、210°和-30°,将曲率表现为极坐标向量形式为k1∠90°、k2∠210°和k3∠-30°。kx、ky分别表示中心线曲率在x轴和y轴上的投影,用k2和k3表示kx和ky,则得到
(5)
(6)
将图2a投影到构节弯曲平面,基于各小节变形情况一致这一特点,利用小节中心线的弧长与拉线长度(lc/n),计算出构节中心线总的弧长为
(7)

(a)参考平面K的构造

(b)平面K在弯曲 平面内投影
2.2 连续体构节变形逆解模型
构节变形的逆解模型是用弧长s、曲率k和偏转角度φ,计算拉线长度l1、l2和l3。设定与平面H平行且过构节末端面最低点的参考平面K,见图3a。将平面K和构节在平面K上面的部分投影到弯曲平面上,则可以得到图3b。
利用β=ks/2n、三角函数与相似原理,可用s、k、φ、d和n表示h2、h3、hc、h1。通过单个构节最内侧弦长加上2n倍的h2、h3、h1,可得到l1、l2、l3的表达式如下
(8)
2.3 连续体构节转化为离散关节变量
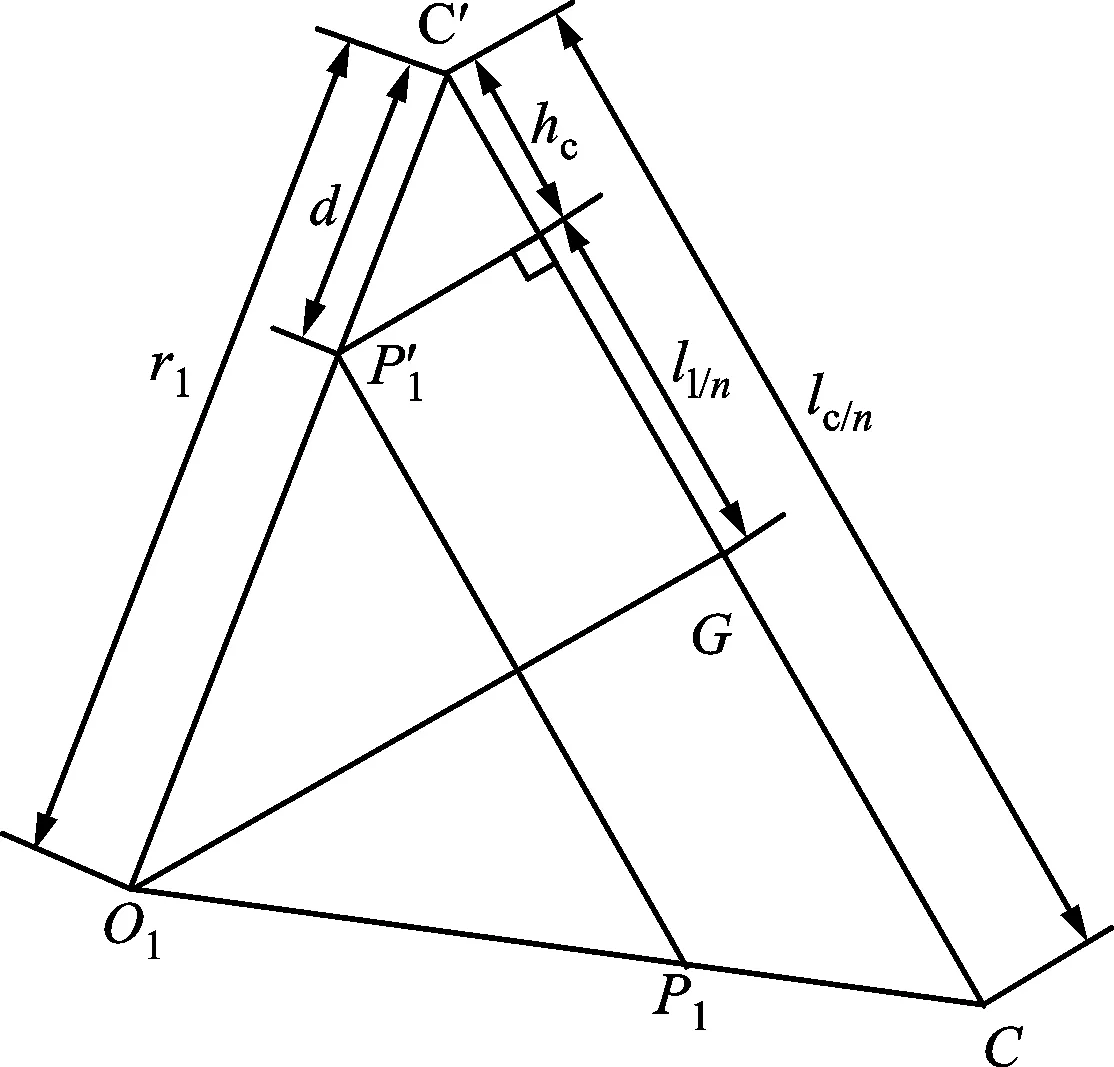
基于等圆弧假设及连续机器人结构特点,用s、k、φ代替传统的平移参数d和旋转参数θ。单个连续体构节可转化为5个关节,如图4所示。
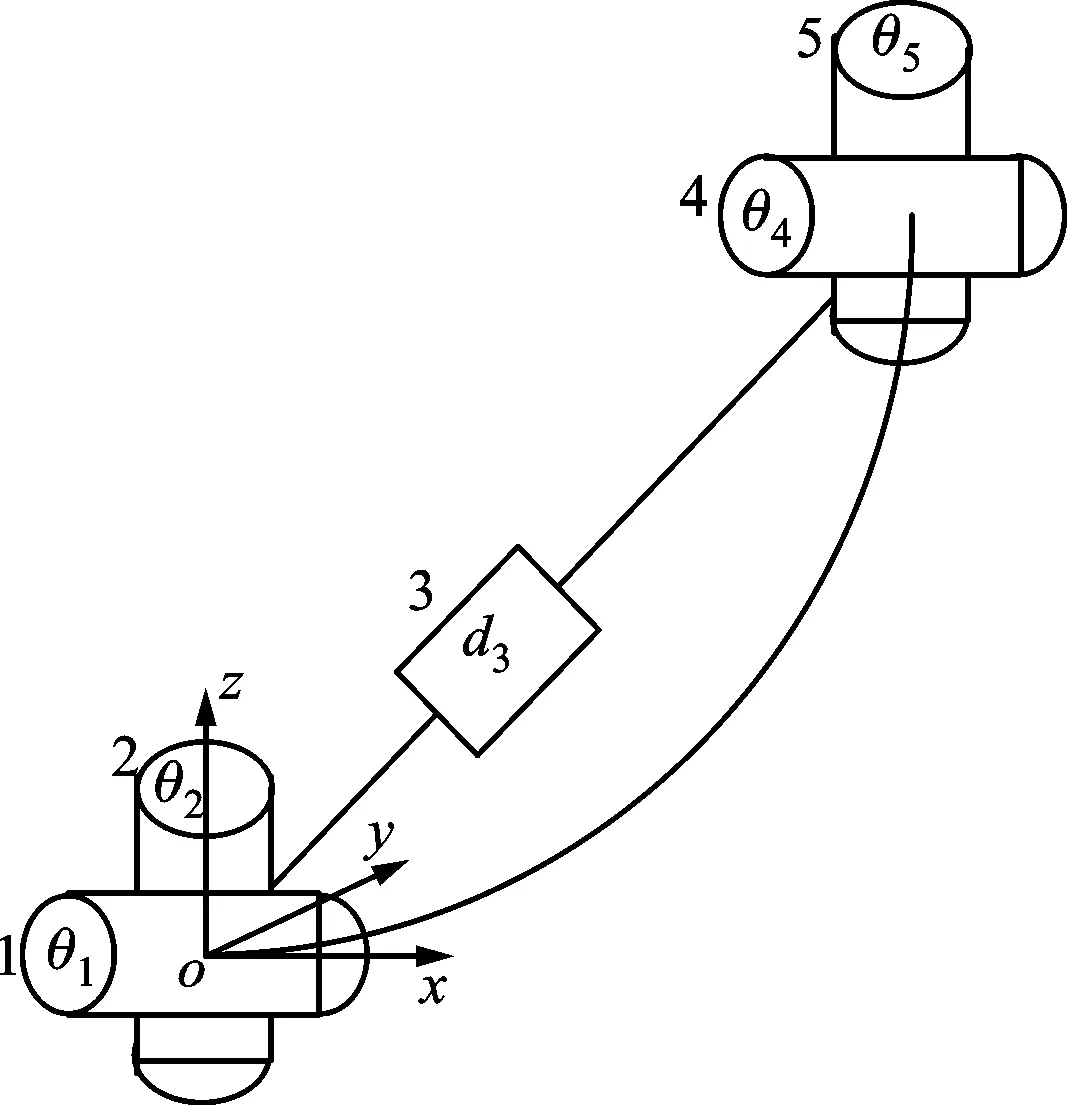
图4 构节转化为离散关节示意图Fig.4 Schematic diagram of transforming section into discrete joints
图4中关节1、2、4、5为旋转关节,旋转角度分别为θ1、θ2、θ4、θ5,关节3为平移关节,平移距离为d3。这样转化主要由于两点原因:引入了旋转关节1表示连续机器人扭转运动,但连续机器人运动过程中并不存在扭转,其仅在不同平面弯曲;引入平移关节3使得最终机器人末端姿态指向其弦的方向,而实际连续机器人末端姿态应沿着其末端切线向外。为了能正确表示机器人的姿态,必须引入与关节1、2对偶的关节4、5,对简化后的连续机器人的姿态进行校正。表1是构节变形参数与离散关节参数对应关系。
表1中θ、α表示关节绕z和x轴旋转,d和a代表关节沿着z和x轴平移量。按照D-H转换法,单构节中第i个关节变换矩阵Ai可表示为
(9)
连续体机器人单构节j的齐次变换矩阵Tj可表示为
Tj=A1A2A3A4A5
(10)
仿象鼻气动连续体机器人包含3个构节,并在末端安装了一个执行器。整机齐次变换矩阵计算式
T=T1T2T3TE
(11)
式中:TE为末端执行器相对构节末端板的平移变换矩阵。通过上述分析便可建立仿象鼻气动连续体机器人的常曲率运动模型。利用该模型,可以根据已知的拉线长度计算出机器人末端位姿。

表1 单构节变形参数与离散关节参数对应关系
3 机器人气动系统和运动控制
使用电气比例伺服阀控制9个气动肌肉内部气压实现机器人的运动,使用开关阀控制末端气爪,实现抓放功能。电气比例伺服阀(ITV)的输出气压与输入电信号成比例,特点是内部集成有PID控制器可对气压进行连续、无级调节。伺服阀输出随控制信号变化如图5所示,当控制信号为方波时,输出气压p与理论值(设定值)的跟随时间小于0.5 s,超调量近似为0,因此只需控制9个伺服阀的输入电信号便可使象鼻型机器人实现连续、平滑的运动。
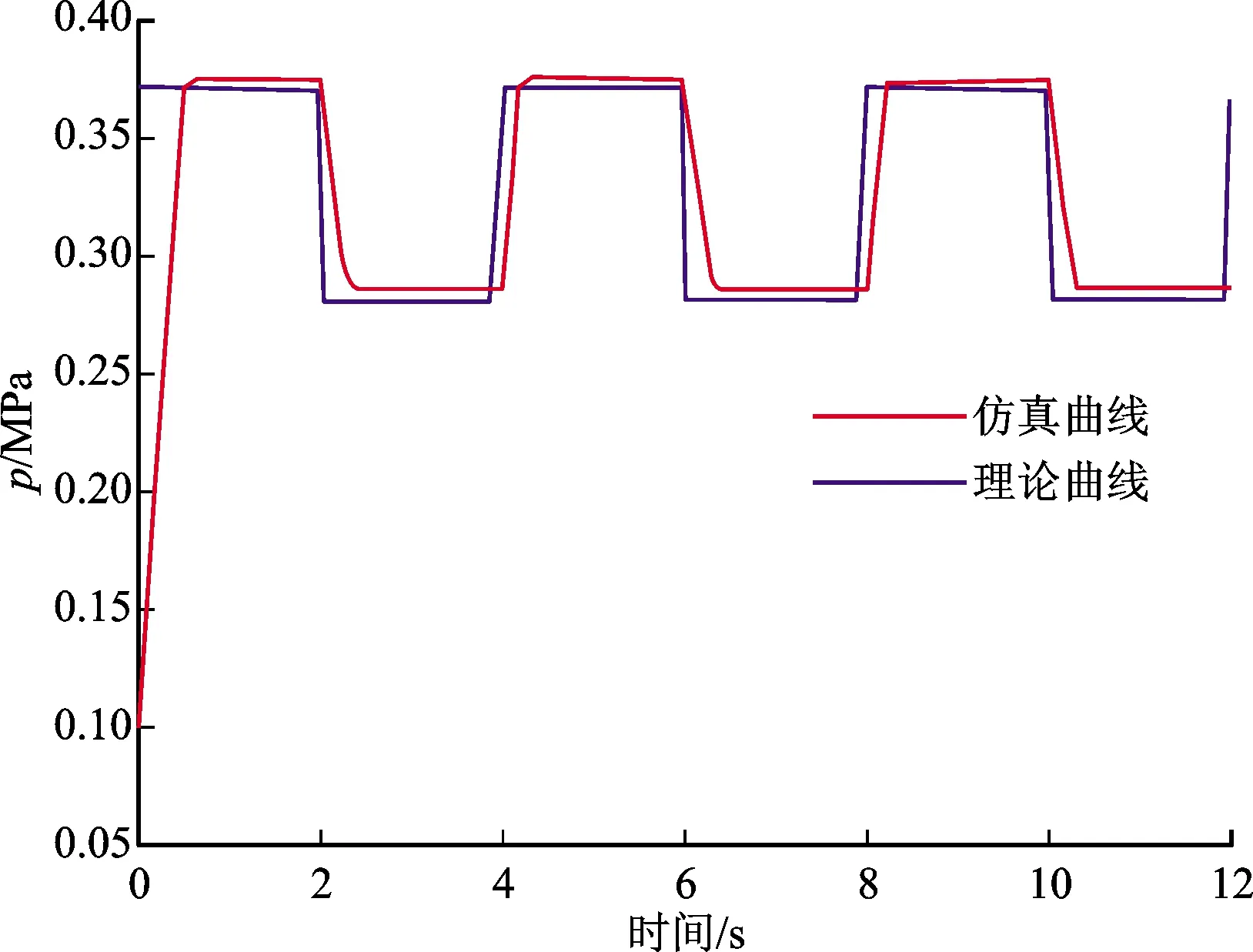
图5 气压伺服阀输出特性曲线Fig.5 Output characteristic curve of pneumatic servo valve
仿象鼻气动连续体机器人采用二级分布式控制系统,通过上位机输入期望的目标姿态或者直接输入一组控制气压,下位机在接收到上位机的数据后,将电压信号传送给电气比例伺服阀和二位三通电磁阀来控制机器人的运动和目标物的抓取。
机器人系统的直接控制量是气压值,运动学模型则是拉线长度和机器人末端位姿之间的关系,因此需要找到气压与拉线长度的关系。控制同一构节3个气动肌肉气压分别独立取0、0.03、0.06、0.09、0.12 MPa,并记录相应拉线传感器值。利用测得的125组数据,分别建立三元线性、三元二次、三元三次回归模型。三元线性回归模型方差为9.2×10-5,相关系数为0.947 4;三元二次函数回归模型方差为1.4×10-5,相关系数为0.979 5;三元三次函数回归模型方差为2.8×10-6,相关系数为0.990 8。采用三元三次函数回归计算并不复杂,对数据拟合也相对精确。图6为机器人的运动控制原理图。

图6 机器人运动控制原理图Fig.6 Motion control process of the robot
4 运动控制实验
图7是仿象鼻连续体机器人实验台照片,主要包括机器人本体、电气比例伺服阀、拉线传感器、计算机以及嵌入式系统等。控制9个气动肌肉的气压不断变化,机器人末端会在工作空间内留下一条轨迹,采用双目摄像机记录机器人末端的坐标,并用拉线传感器测量对应点的肌肉长度,得到的数据见表2。

图7 仿象鼻气动连续体机器人实验台照片Fig7 Experimental bench of pneumatic trunk-type continuum robot
将表2中的数据带入到常曲率运动模型中,计算出相应的坐标,将计算结果与摄像机测得坐标一起绘制成图,如图8所示。双目摄像机测得坐标为(0.02,0.27,-0.78)(0.02,0.297,-0.755)(0.03,0.335,-0.695)(0.03,0.366,-0.6)(0.03,0.415,-0.545)(0.03,0.449,-0.475),常曲率计算的坐标为(0.021 4,0.285 0,-0.718 4)(0.022 7,0.302 3,-0.703 3)(0.026 3,0.351 1,0.655 7)(0.030 2,0.403 5,-0.598 7)(0.033 1,0.441 7,-0.514 0)(0.034 6,0.461 6,-0.441 7),二者的误差向量e为[0.063 4,0.052 0,0.042 6,0.037 5,0.041 0,0.035 9],单位为m。
从图8看出,将常曲率模型运用到象鼻型机器人时,计算的运动轨迹与实际轨迹大致相同,但二者存在一定误差。越靠近工作空间下方底部位置, 各构节弯曲变形程度越小,此时构节中心线越不接近常曲率或者算出的曲率值相对误差越大,造成位置最大误差约为6.3 cm。越靠近工作空间上边缘的位置,构节弯曲程度越大,越接近常曲率,此时模型精度越高。为了进一步验证常曲率模型的精度,随机获取一组机器人拉线数据[l1,l2,…,l9]=[21.0,27.1,20.7,17.3,26.3,16.5,15.8,26.7,15.6] cm代入常曲率模型,得到点A(0.374,0.313,-0.264) m并在该点处放置网球(直径为6.5 cm)。由三元三次拟合模型计算出控制气压,控制机器人完成对目标物的抓取、向上偏转运动避障、再将目标物放到机器人实验台竖直下方一系列动作,气压变化与抓放过程照片见图9。重复进行十余次上述过程机器人均能成功抓放网球,这说明,在一定精度范围内可以采用常曲率模型实现对仿象鼻气动连续体机器人的运动位姿控制。
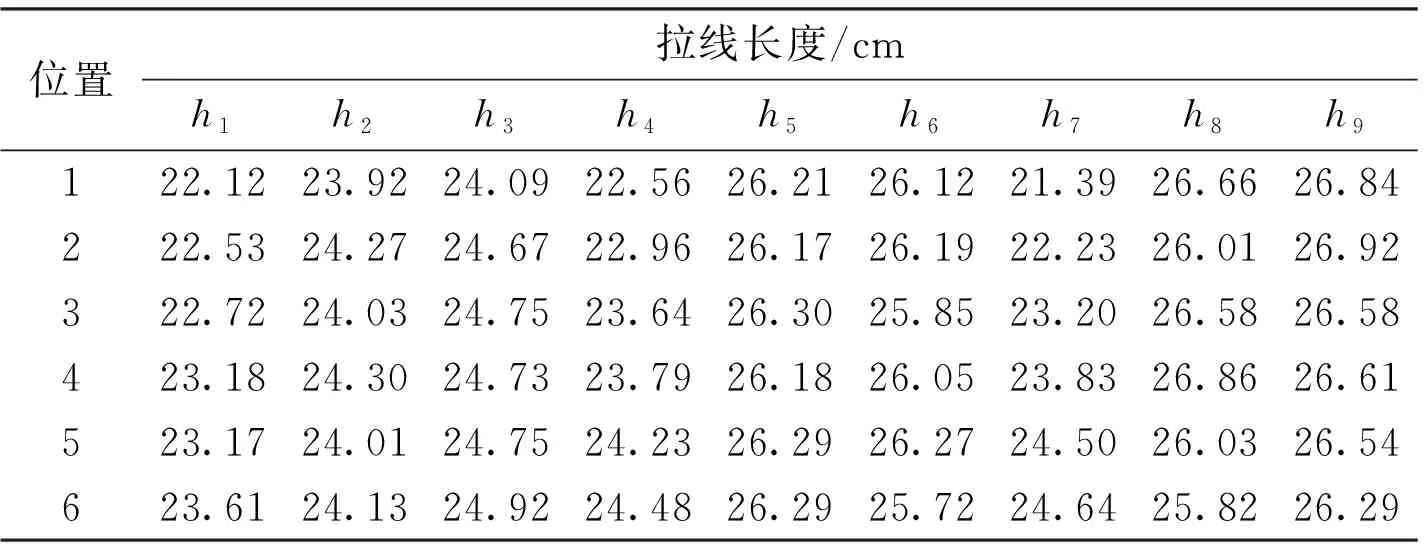
表2 机器人末端位置与拉线长度数据表

图8 机器人末端的计算轨迹与实际轨迹图Fig.8 Computational and actual trajectories of the robot’s actuator
通过有目标地控制9根气动肌肉的气压,记录末端执行器坐标,可得到机器人实际工作空间,在xoz平面内工作空间截面如图10a所示。对比之前采用蒙特卡罗方法[25]随机选取气压值,在三构节连续体机器人常曲率仿真模型中,仿真计算获得的工作空间截面,见图10b。由图可知,仿真计算工作空间与其实际工作空间基本一致,主要区别在于两侧对称性,这是由于仿真忽略了“机器人的结构是120°旋转对称而非轴对称”。在本机器人结构方案设计阶段,曾对四构节和五构节连续体机器人的运动空间作了分析,见图10c、10d。可以看出,仿真得到的四构节、五构节连续体机器人的运动空间的基本形状与三构节类似,呈“倒伞/球状”的特点。构节数量越多机器人的柔性越高,运动范围越大且位姿更加多样,总体工作空间越接近球状。综合上述实验结果可以看到,通过本文确定参数的常曲率模型可以用于本气动连续体机器人的位姿预测与运动控制,且其误差在可接受的范围内。

(a)抓取过程控制气压变化曲线

(b)抓放运动过程视频截图图9 机器人对目标物抓放的运动控制实验Fig9 Motion control experiment of robot grasping and releasing a target object
机器人运动实验误差的来源主要有以下3个方面:①系统误差,主要是机器人本身误差,机器人结构上有许多非标准件,这些误差导致机器人的结构不是严格一致。②测量误差,拉线传感器的数据不是气动肌肉真实长度,二者存在误差;摄像机与拉线传感器自身的测量精度,也会导致位姿计算存在误差。③模型误差,常曲率模型忽略了机器人自重与负载,但本文采用拉线传感器采集实际各构节变形数据,用于确定常曲率运动模型参数,事实上抵消了忽略自重和负载的负面影响,使所建运动模型更加贴近实际。进一步,可从减小上述3个误差入手深入开展研究工作。

(a)3构节实际工作空间截面
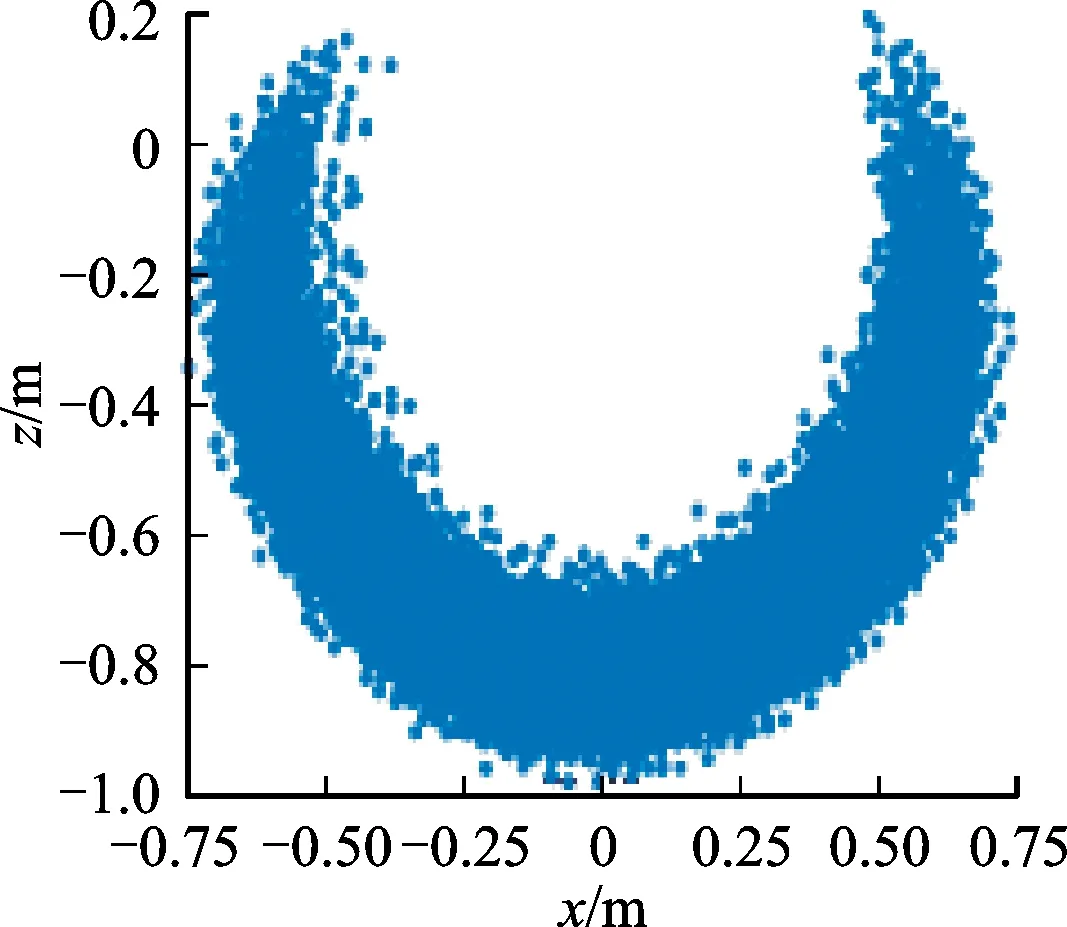
(b)3构节仿真工作空间

(c)4构节仿真工作空间
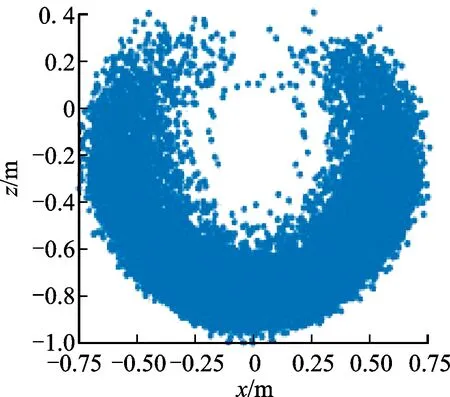
(d)5构节仿真工作空间图10 3~5构节机器人工作空间的截面图Fig.10 Workspace of robot with 3-5 sections
5 结 论
(1)在常曲率的假设下,通过几何变换推导可以得到仿象鼻气动连续体机器人的常曲率运动模型,得到拉线长度与机器人末端位姿的关系。该项研究为该类机器人的运动控制奠定了理论基础。
(2)采用拉线传感器采集机器人构节变形及末端位姿数据,用于确定常曲率运动模型参数,使所建运动模型更加贴近实际。通过所设计的目标物抓放实验表明,采用本文方法确定模型参数的常曲率模型,可实现仿象鼻气动连续体机器人的位姿控制。
(3)由于结构和材料特殊性,对软体机器人的位姿进行精确控制较为困难。本文的仿真计算和实验结果,以及确定常曲率模型参数的方法可以为同类或其他软体机器人的运动控制提供重要参考。

