伺服系统瞬态优化的模糊自适应深度强化学习方法
魏晓晗,张庆,2,蒋婷婷,梁霖,2
(1.西安交通大学机械工程学院,710049,西安; 2.西安交通大学现代设计及转子轴承系统教育部重点实验室,710049,西安)
learning; fuzzy control
伺服系统将控制信号转化为精确的机械运动,是机电装备向智能化、高精度和高效率发展的关键基础,也是生产制造数字化的核心载体。永磁同步电机(PMSM)具有密度大、几何尺寸小、重量轻、响应快、调速范围宽、控制方便等显著优点,已成为伺服系统中将电能向可控机械运动转化的最佳选择之一[1-4]。现代高精度生产线要求伺服系统能够稳定快速地达到控制目标,因此以平滑无超调与快速响应为中心的瞬态响应能力成为评价PMSM伺服系统性能的重要指标[5],也成为电机控制优化的研究热点。
PMSM伺服系统通过对电机的精确控制实现高精度加工要求,控制优化是目前研究的关键问题。胡强晖等采用全局滑模和变指数趋近率之间的切换控制,有效地消除了永磁同步电机伺服系统的抖振现象,但是由于包含大量的超参数,应用难度较大[6];吴振顺等提出一种模糊自整定PID控制器,对抑制干扰和噪声有一定的效果,但并没有考虑瞬态响应速度,整体性能优化效果有限[7];蔚永强等采用径向基神经网络对系统进行自适应补偿[8],有效地改善了直驱式伺服系统中稳态跟踪性能降低的问题,但仅限于仿真研究。由于传统方法在多目标优化能力的限制,现阶段对于伺服系统的研究仍局限于稳态误差消除与鲁棒性提升,然而对于高精度加工而言,提升系统响应速度与抑制超调同等重要。
作为一种适用于多目标优化的方法,深度强化学习方法搜索能力强、收敛速度快,在控制领域展现出了非常高的应用价值。Pane等结合Actor-Critic算法以及3D打印机伺服控制系统提出了一种针对伺服系统的稳态误差补偿方法[9]。陈奇石等针对双足机器人稳定行走问题,使用有监督学习中的稀疏在线高斯过程回归方法对强化学习中的函数进行拟合,实现了双足机器人快速、稳定行走的步态规划[10]。Han提出了一种基于强化学习的在线演化框架来预先检测和修改自动驾驶汽车控制器的不完善决策,兼顾了速度与安全性[11]。由于伺服系统瞬态性能优化中存在建模难度高、仿真运算量大导致优化效率低下的问题,深度强化学习尚未应用于这一领域。
在强化学习中,如何权衡知识的“探索”与经验的“利用”是影响强化学习效率与准确性的重要因素,也是贯穿于强化学习发展史并关系到应用效果的关键性问题。针对这一问题,Schaul等提出了经验回放方法[12],即根据重要性对经验池中过往经验样本进行采样。该方法避免了强化学习方法中随机抽取的弊端,提高了算法的收敛速度和准确性,但仅限于Q-Learning方式的强化学习算法,无法应用于采用神经网络等非线性策略的近似算法。作为经典的智能控制方法,模糊控制在强耦合复杂模型的控制问题中具有良好的技术优势,通过采用类似优先级采样的策略,有效改善了随机性采样缺陷。因此,通过模糊控制平衡“探索”与“利用”这一对复杂矛盾,是提高强化学习在控制优化领域应用能力的可行思路。
本文以伺服系统瞬态性能提升为目标,提出一种模糊深度强化学习算法,利用异步优势演员-评论家强化学习算法并行运算效率高、收敛速度快、搜索能力强的特点,结合模糊算法在复杂系统控制中鲁棒性强、适应性高的优势,建立基于模糊自适应深度强化学习的伺服系统瞬态性能优化方法。基于PMSM伺服系统的仿真计算模型,优化瞬态性能参数,并将模型计算参数应用于实际伺服系统。经验证,该方法有效缩短了永磁同步电机伺服系统调节时间,同时抑制了超调与稳态误差的产生。
1 问题分析
1.1 永磁同步电机伺服系统
永磁同步电动机主要由三相绕组固定定子和永磁体磁极转子组成。当三相交流电源供给定子绕组时,产生旋转磁场。旋转磁场与转子上的磁极相互作用产生电磁转矩,激发转子同步旋转。永磁同步电机原理如图1所示。
三相静止坐标系与两相静止坐标系下的定子磁链方程是关于角度θ的时变方程,为方便控制器设计,一般在交直轴两相旋转坐标系下对永磁同步电机进行分析。
在交直轴两相旋转坐标系下,伺服电机交直轴电压方程为
(1)
式中:ud为直轴电压;uq为交轴电压;Rs为定子绕组的电阻;id为直轴电流;iq为交轴电流;Ld为直轴等效电感;Lq为交轴等效电感;ψf为永磁体磁链;ω为转子角速度。
本文永磁同步电机伺服系统矢量控制原理采用id=0控制。在id=0控制方式下,直轴电压转化为
ud=-ωLqiq
(2)
直轴的电流为0时,不再贡献转矩电压。这时电机的所有的电流全部用来产生电磁转矩,只用需要控制交轴电流iq就可以控制电机的转矩,从而实现交直轴电流的静态解耦。
1.2 PMSM伺服系统瞬态响应
随着PMSM伺服系统在工业生产中的广泛应用,日益增长的高精度生产需求要求其动态响应能力快速提升。作为强耦合系统,PMSM伺服电机与负载系统的匹配质量直接影响电机启、停过程中的机电耦合状态,从而影响电机的响应能力。在PMSM伺服系统中,存在电动机驱动、控制参数与力学输出参数、电动机力学输出参数与负载系统等耦合关系,其中电机力学输出与负载耦合方程如下
(3)
(4)
式中:p为电机极对数;ψd为直轴等效磁链;ψq为交轴等效磁链;Te为电磁转矩;TL为负载扭矩;B为阻尼系数;J为转动惯量。
在伺服系统瞬态响应优化中,快速性和稳定性是控制的核心目标。从式(3)(4)可以得出,电机响应的快速性由转子角速度ω及其微分决定,而响应的稳定性则取决于电机输出转矩、角速度及其微分参数之间的平衡状态。因此,实现伺服电机动态性能优化,需要从伺服系统中的机电耦合关系出发,通过调节电动机的驱动、控制参数,改变电机运动形态,进而影响电动机力学输出参数,从而实现电动机在特定载荷下快速性与稳定性的平衡,使电机与负载系统达到最佳匹配状态。
随着相关研究者对PMSM的深入研究,许多对于闭环控制参数的优化控制方法如滑模变结构控制、模糊控制和自适应控制等[13-16],位置的响应速度与控制精度得到了显著的提升。传统参数整定寻优算法无法兼顾包括响应速度和控制精度在内的多个控制目标,或对于复杂耦合问题搜索能力欠佳,因此难以解决伺服系统中复杂耦合关系下的驱动、控制系统参数优化问题。寻求一种适用于多目标、多参数、复杂耦合问题的控制优化方法,是解决永磁同步电机伺服系统瞬态性能优化问题的关键。
作为一种适用于复杂控制、决策问题的机器学习算法,深度强化学习算法[17-18]在解决多目标、多参数问题中具有收敛效率高,稳定性强的优势,使之成为解决PMSM伺服系统瞬态性能优化问题的可行方案。在本文针对伺服系统瞬态性能优化问题,对强化学习算法进行模糊自适应改进,提高收敛速度以满足实际应用中时效性的要求。
2 模糊自适应深度强化学习方法
2.1 强化学习原理
强化学习是一种数据驱动的在线启发式机器学习方法,是行为主体从环境到行为映射的学习[19]。作为一种仿生算法[20],在强化学习中,智能体通过与环境交互实现学习过程。智能体从环境中以状态信号的形式接收状态信息,并根据策略函数π(s,a)采取相应的动作。策略函数π往往是随机的,通过与奖励函数结合实现对每一个可能的状态转换的评估,并根据概率选取动作。在算法的每一步执行动作时,环境将受到动作影响,根据状态转移函数与奖励函数转移到下一个状态s′,并得到瞬时奖励rt。根据状态St计算得到神经网络输出Vt作为本状态价值函数的估计,由新状态St+1更新输出Vt+1。经过N步后完成一个回合的运算,并得到回报函数Gt。根据Bellman方程,价值函数定义为t时刻状态St能获得的回报期望,其表达式如下
Eπ{rt+γVπ(St+1)|St=s}
(5)
式中:γ为折扣因子。
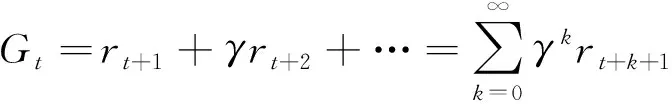
(6)
式中:A(s)为动作空间;p(s′,r|s,a)=Pr{St+1=s′,rt+1=r|St=s,At=a},即在状态St=s下实施动作At=a,得到下一个状态St+1=s′与奖励rt+1=r的概率。
在强化学习中,迭代运算的目标在于训练得到最优控制策略π(s,a)最大化累计奖励G。以价值函数最优化为方向进行迭代,即可实现累计奖励最大化。
2.2 异步优势演员评论家(A3C)算法
异步优势演员-评论家(A3C)算法是一种基于并行计算和Actor-Critic算法的深度强化学习算法。其中Actor-Critic算法包括Actor和Critic两个网络,Actor是一个以策略为基础的网络,通过奖惩信息调节不同状态下采取各种动作的概率;Critic是一个以值为基础的学习网络,可以计算每一步的奖惩值。二者相结合,在不断迭代中,得到每一个状态下选择每一动作的合理概率。在A3C算法中,创建多个并行的环境,每个并行环境同时运行Actor与Critic网络,让多个拥有副结构的智能体同时在并行环境上更新主结构中的参数。并行运算中的智能体互不干扰,而全局网络的参数更新则通过每个本地网络分别上传的运算后的更新梯度实现,这种更新方式降低了算法中经验之间的相关性,因此收敛性显著提高。
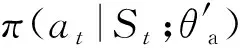
(7)

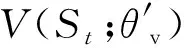
策略函数π(at|St;θ′)的损失函数为
cθ′H(π(St;θ))
(8)
式中:cθ′H(π(St;θ))为策略π(at|St;θ′)的熵项;价值函数的损失函数为
(9)
对参数进行梯度更新时,Actor网络和Critic网络采取的策略分别为
cθ′H(π(St;θ))
(10)
(11)
根据该更新策略迭代后输出最终的动作结果。
2.3 模糊自适应深度强化学习算法
在工业应用中,伺服系统由于工况复杂多变以及在寿命周期中的状态变化等问题,优化控制时需要考虑实时性需求,对强化学习算法的计算效率提出了更高的要求,因此必须对强化学习中的“探索”与“利用”机制进行综合平衡。参考生物对于经验的记忆程度的区别,采用的改进策略为:区分经验的优先级重要性,并根据经验的优先级对经验区别记忆。
针对包括Q-Learning在内的所有强化学习算法,区分经验重要性并实现记忆区分的一种可行思路为:通过经验中动作得到的奖励来区分经验重要性,并根据重要性调整学习率,从而实现经验记忆的优先级更新。这种方法借鉴大脑对于不同记忆的深刻程度的区别,对于“非同寻常”的经验印象更加深刻,而对于“司空见惯”的经验则记忆程度较低,能够保证生物在进行正常学习的同时保持对异常现象的警觉性,从而使生物获得的知识更全面。在强化学习中,动作奖励表示智能体所采取动作的优劣,而学习率影响每条经验的更新程度,即记忆程度。相应地,对于获得收益或惩罚较大的经验采用较大的学习率,对于其他一般经验采用较小的学习率,以期在提高收敛速度的同时保证准确性。
为实现该策略,需要寻找一种行之有效的手段,以得到经验优先级与记忆深度之间的映射。模糊控制算法[21]自1965年提出以来,广泛应用于工业控制领域,模糊隶属度作为多因素影响下的综合决策评价函数,在系统性能优化方面体现出强大的优势。因此,在强化学习过程中建立模糊控制器,解决经验优先级与记忆深度的平衡问题。针对奖励偏差及其变化率建立论域[-e,e],通过隶属度函数运算得到输入值的模糊语言,在模糊控制规则的条件语句中搜索对应学习率控制量的模糊语言,最后对控制量模糊语言进行清晰化,从而将推理得到的学习率控制量转化为学习率输出。算法流程如图2所示。
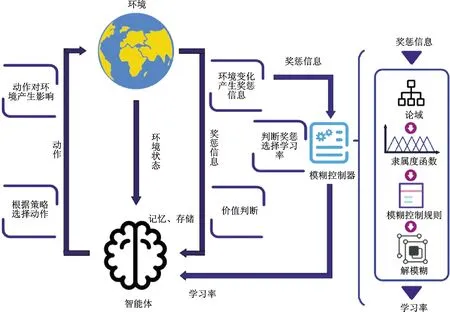
图2 模糊自适应深度强化学习算法流程Fig.2 Fuzzy adaptive reinforcement learning algorithm flow
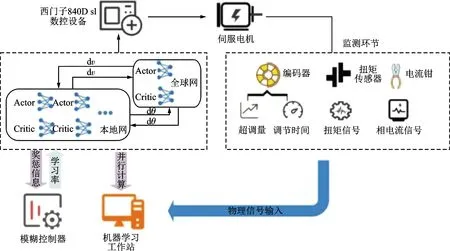
图3 基于模糊自适应深度强化学习算法的伺服系统瞬态性能优化Fig.3 Transient performance optimization of servo system based on fuzzy adaptive deep reinforcement learning algorithm
3 瞬态性能优化方法
在伺服系统瞬态性能优化中,需要同时考虑响应的快速性与稳定性两个方面,使系统响应速度得以提升,同时避免演化为欠阻尼系统产生超调量。针对该问题,基于深度强化学习的永磁同步电机伺服系统瞬态性能优化方法在PID环节中设计补偿环节,根据缩短调节时间、抑制超调量的多个控制目标建立评价指标,利用评价指标设计A3C算法奖励函数,并根据控制补偿环节确定A3C算法动作参数,确定最优补偿参数。
如图3所示,在机器学习工作站中建立伺服系统仿真模型,并根据实际伺服系统参数及运行结果拟合仿真模型,减小模型与系统偏差;建立A3C强化学习算法全局及本地Actor-Critic网络,根据缩短调节时间、抑制超调量的控制目标建立强化学习价值函数;在A3C强化学习算法中引入学习率模糊控制器,根据经验优先级调整学习率,提高运算效率。
3.1 价值函数设计
瞬态性能综合优化的目的在于缩短调节时间、抑制超调量,同时保证正常工作效率。因此,建立伺服系统调节时间ts、超调量σ%、效率指标η(电流与扭矩有效值之比)3个瞬态响应性能指标作为算法评价指标。设置评价指标向量即状态向量
St={σ%,ts,ηs}
(12)
其中
(13)
ts=t′
(14)
(15)
式中:ctp为伺服系统位置时域响应最大偏离值;c∞为伺服系统位置时域响应终值;t′为伺服系统位置时域响应稳定至终值98%所用的时间;Trms为伺服系统扭矩时域响应有效值;Irms为伺服系统电流时域响应有效值。
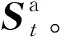
(16)
式中:i1、i2、i3为重要性因子。设置奖励函数和线性补偿函数为
(17)
(18)
式中:Rref为奖励函数参考向量;td为补偿截止时间。选择补偿放大增益K作为算法输出动作,作为Actor网络的输出,st和K作为Critic网络的输入。
3.2 Actor-Critic网络设计
由于径向基神经网络逼近精度高、结构简单、线性拟合,以及便于进行微分运算的特点,在Actor与Critic网络的参数化设计中采用该网络。
根据输入状态及动作分别设计Actor-Critic算法中Actor与Critic参数化网络参数φ(s),在[0,1]中等间隔设置神经网络中心,随机配置初始Actor网络权值参数θ与Critic网络权值参数ωi。径向基神经网络形式如下
(19)
式中:ci为径向基中心;n为隐含层网络节点数;k为输入层节点个数。
对网络参数ωi进行偏导运算
(20)
使用径向基网络设计的Actor-Critic网络,在进行梯度更新时,能够快速地通过微分运算得到新参数,从而提高计算效率。运行A3C算法迭代至收敛,即可得到伺服系统补偿参数。
3.3 模糊控制器设计
模糊控制器的设计包括论域划分、确定模糊集合、隶属度函数求解、模糊规则推理和解模糊等步骤。定义给定的奖励偏差为本回合本步收益与前N回合平均收益值之差,根据运算经验,设定奖励偏差e、变化率ec及输出值学习率rl的基本论域。输入量与输出量所取的模糊子集的论域都为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6},对应的模糊语言为{负大、负中、负小、零、正小、正中、正大}。隶属度函数选用三角形函数的形式,三角形隶属度函数分布曲线如图4所示。

图4 三角形隶属度函数分布曲线Fig.4 Triangular membership function distribution curve
三角形隶属度函数表达式如下
(21)
本文基于三角形隶属度函数a(u)设计输入与输出量隶属度函数A(u)如图5所示,图中{NB,NM,NS,ZO,PS,PM,PB}对应模糊语言{负大、负中、负小、零、正小、正中、正大}。
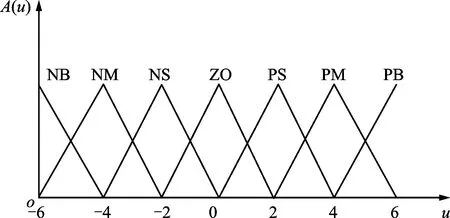
图5 输入量与输出量隶属度函数Fig.5 Membership function of input and output
根据隶属度函数可以得到特定奖励偏差e及其变化率ec对应的模糊语言。在进行模糊推理时,需要考虑在不同情况下奖励偏差e及其变化率ec的模糊语言之间的逻辑关系,并根据逻辑关系确定模糊推理结果。因此,根据学习率整定的工程经验建立模糊推理规则表,如表1所示。
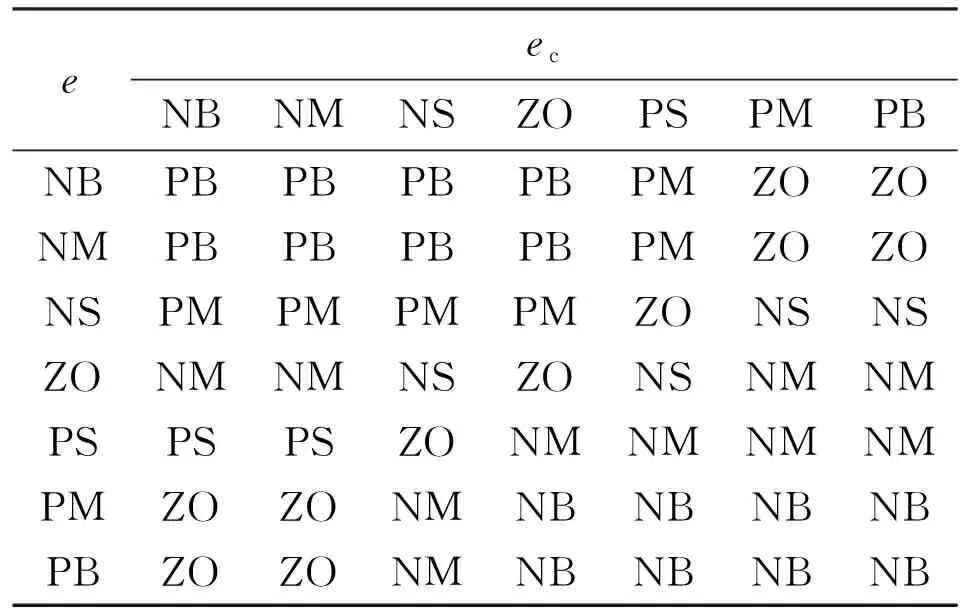
表1 输出值模糊规则表
表1中任意一条规则都可表示为IFeisAi1andecisAi2, THENrlisCi的形式。通过上述的逻辑及条件推理,总共可以将模糊规则表总结为49条模糊控制条件语句。
为得到精确输出值,需要根据学习率的模糊语言,结合隶属度函数,通过面积中心法对输出值进行反模糊化。面积中心法表达式如下
(22)
通过反模糊化,得出学习率rl的精确输出U。
4 仿真实验
为提高运算效率,同时确保系统安全性,本文利用仿真运算得到优化参数,在仿真模型中验证优化效果,继而应用于实际伺服系统。选择西门子840D sl数控系统为实验对象,包括驱动器、控制器、执行器与检测器件4个部分,控制参数如表2所示。
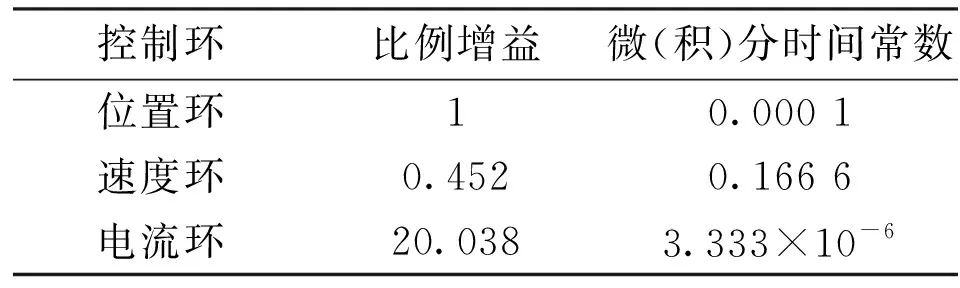
表2 西门子840D sl数控系统控制参数
驱动电机为西门子1FK7083-2AF71-1AA0永磁同步电机,参数如表3所示。
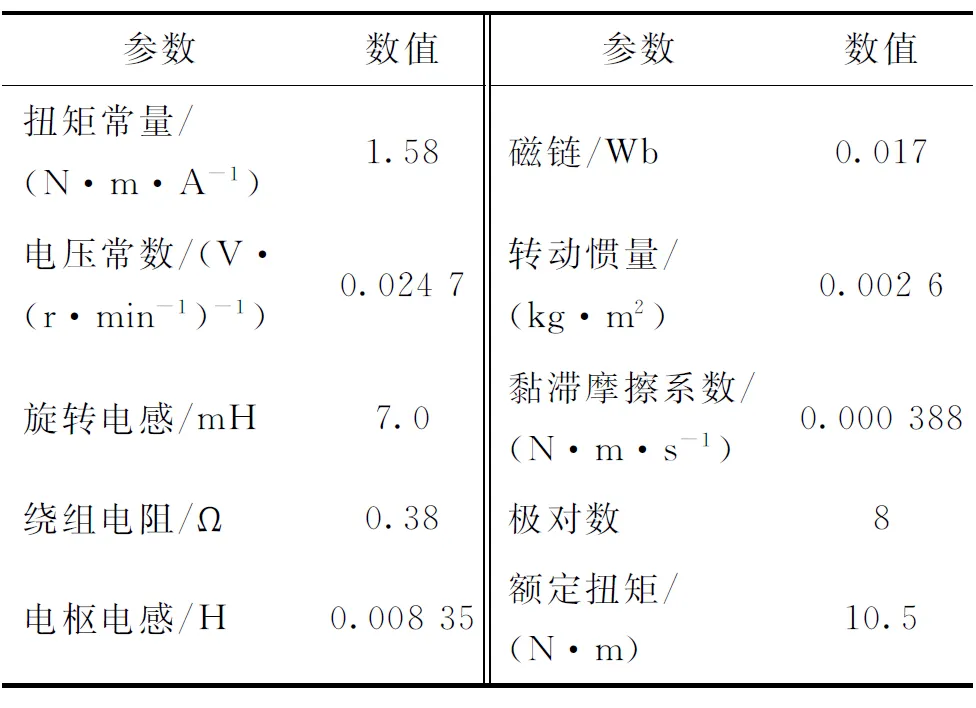
表3 永磁同步电机设计参数
4.1 伺服系统仿真模型
在Simulink仿真环境中,对PMSM伺服系统建立如图6所示的仿真模型,包括PID控制器、被控对象、执行、检测、比较、补偿6个环节。该伺服系统仿真模型采用位置控制方式,主要由通用电桥模块、永磁同步电机模块、空间矢量脉宽调制模块、PID控制器、坐标变换模块5个模块组成,模拟840D sl数控系统驱动进给轴运动过程。
根据伺服系统电机硬件参数与控制参数配置仿真模型,使模型逼近真实伺服系统。参照表2及表3,配置图7所示模型,经过仿真运算,得到相同行程下伺服系统运动轨迹。以600 mm行程为例,轨迹曲线如图7所示。
实际伺服系统±5%的调节时间为7.06 s,而仿真伺服系统±5%的调节时间约为6.47 s,两者差距为8.49%;实际伺服系统上升时间约为5.32 s,仿真模型上升时间约为5.02 s,两者之间差距为5.97%。本文所用到的仿真模型为简化模型,而西门子840D sl系统中存在复杂的驱动参数与通道控制参数,这导致伺服系统实际运行相应曲线与仿真曲线形状上略有差异,但从瞬态响应性能方面可以认为二者性能相近,符合实验要求。
4.2 结果及分析
进行仿真运算,加入模糊控制器后算法在大约第53回合收敛,最大奖励值为13.58,而未加入模糊控制器时算法大约在152回合收敛,最大奖励值为13.53。这表明,在加入学习率模糊控制器后,收敛准确性未受影响,而收敛速度得到提升。迭代过程中奖励函数变化与未加入模糊控制器变化表现对比如图8所示。
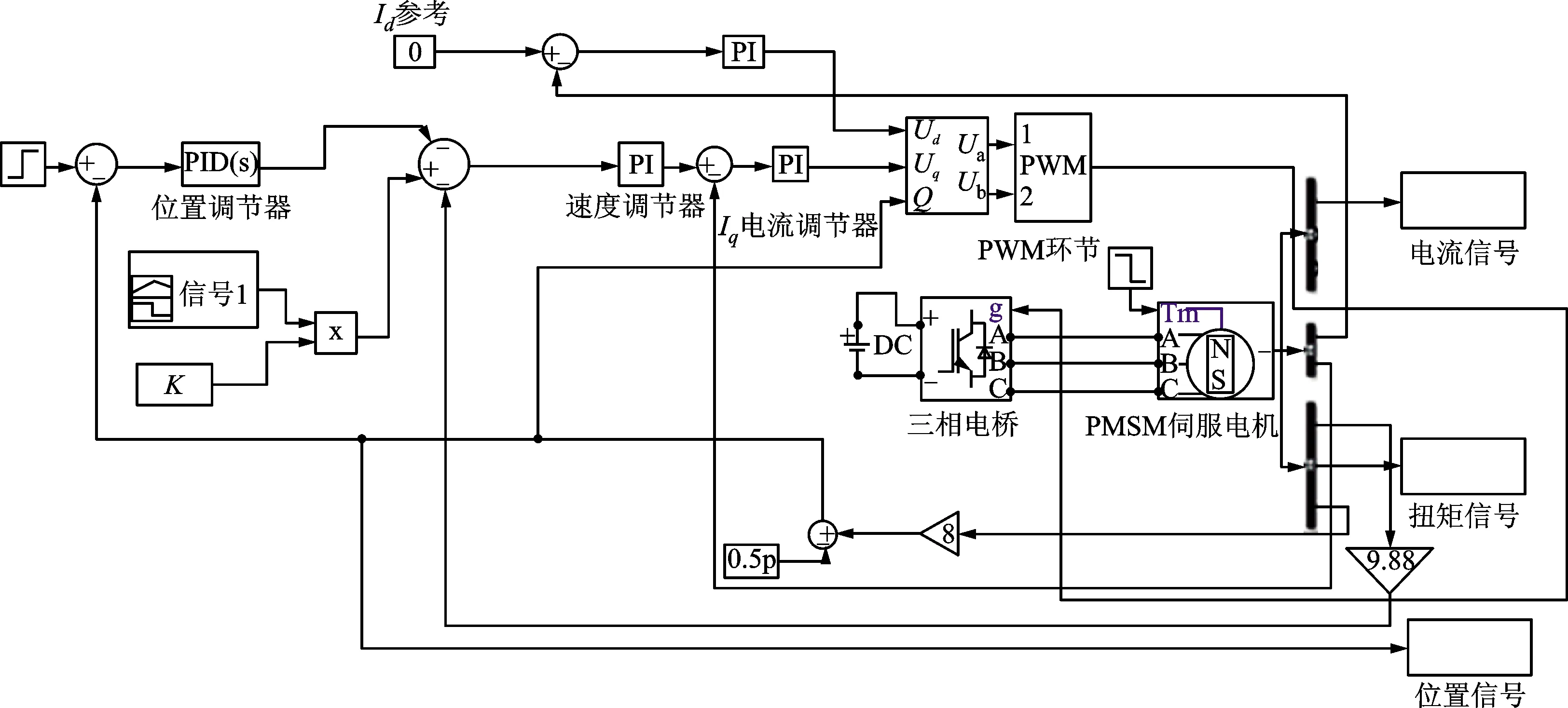
图6 永磁同步电机伺服系统Simulink仿真模型Fig.6 Simulink simulation model of permanent magnet synchronous motor servo system

图7 仿真模型与伺服系统响应曲线对比Fig.7 Comparison of simulation model with servo system response
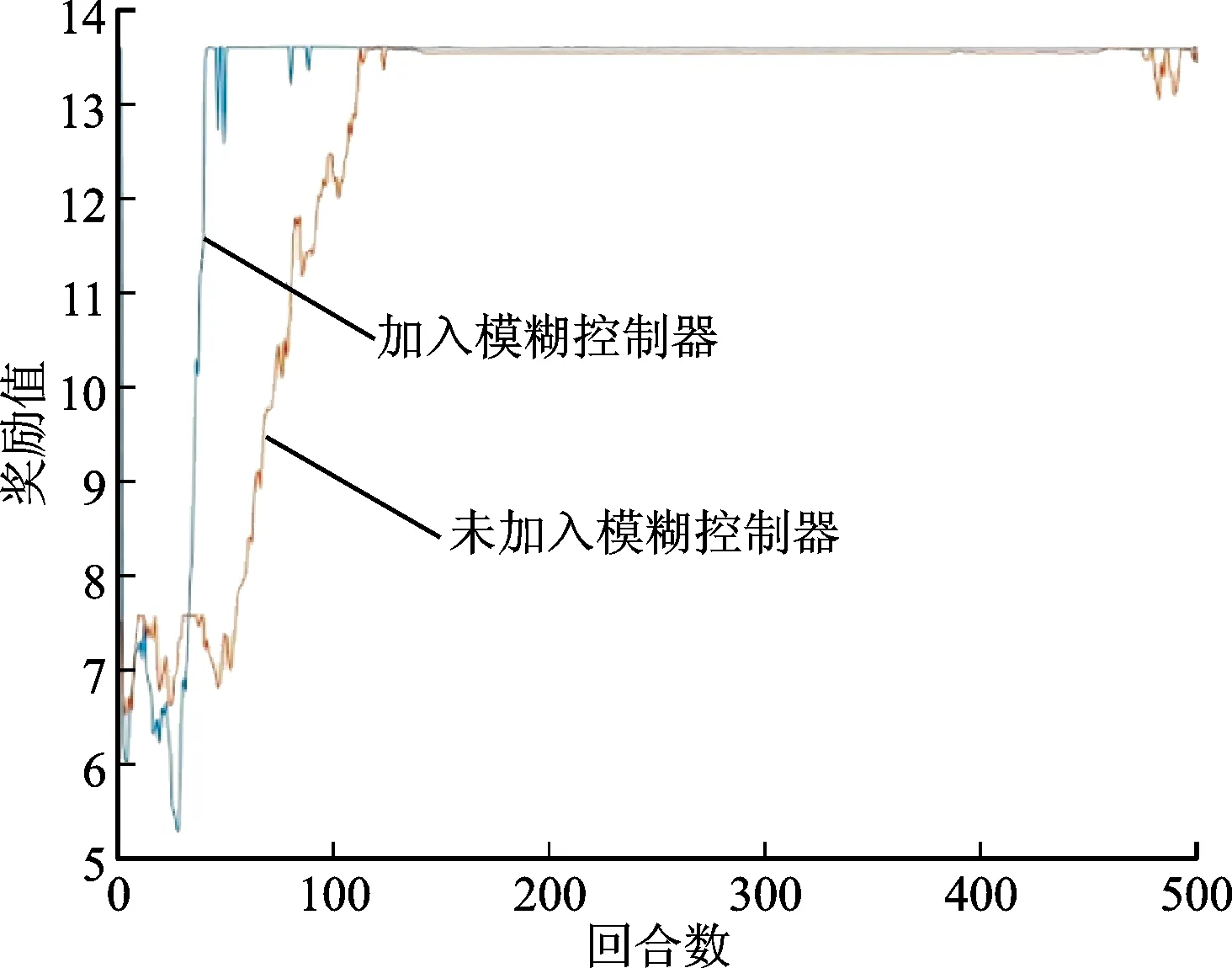
图8 优化仿真奖励函数变化过程对比Fig.8 Comparison of reward function change process in simulation
经过运算得到最优补偿增益K=53.564 5,加入补偿增益得到仿真补偿运行结果与原始运行结果对比如图9所示。根据响应曲线可以得出仿真前后主要响应指标如表4所示,补偿前的伺服系统调节时间为5.02 s,超调量为0;补偿后的调节时间为4.13 s,超调量约为0.3%。在未引入明显超调的前提下,调节时间缩短17.72%。
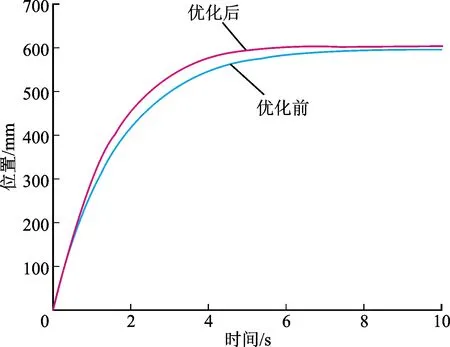
图9 仿真模型优化效果对比Fig.9 Comparison of simulation model optimization effects

表4 仿真系统优化瞬态响应指标对比
由仿真结果可知,模糊自适应深度强化学习伺服系统瞬态优化方法可以成功提高系统响应速度,伺服系统的调节时间和效率都有不同程度的提升。加入模糊控制器,在未影响算法准确性的同时,大幅提升了运算效率。
4.3 系统应用
实际系统如图10所示,包括SINAMICS S120驱动系统、SIMATIC S7-300 PLC 控制系统与HMI人机交互系统,负载装置选用三菱ZKB-XN磁粉制动器。

图10 西门子840D sl数控系统试验台Fig.10 Siemens 840D sl CNC system test bench
将仿真实验得到的优化参数输入实际数控系统中,运行数控伺服系统后得到补偿前后伺服系统响应对比如图11所示。补偿前的调节时间为5.32 s,超调量为0;补偿后的调节时间为4.75 s,超调量为0。优化后在没有引入超调的前提下,系统位置调节时间缩短10.71%。优化前后响应指标对比如表5所示。

图11 伺服系统实验台优化响应曲线Fig.11 Effect of servo system optimization
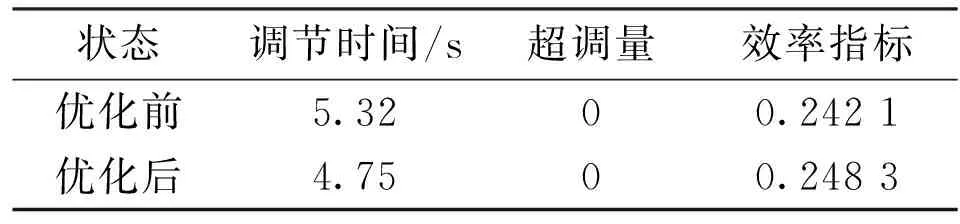
Table 5 Comparison of transient response indexes for optimization of servo system test bench
由实验可以得出,模糊自适应深度强化学习方法针对缩短调节时间与抑制超调的多目标优化问题,明显提升了实际伺服系统瞬态性能。在引入瞬态性能并行优化运算得到的优化参数之后,伺服系统的调节时间有较大程度的缩短。与此同时,补偿优化并没有引入额外稳态误差,对超调也有一定的抑制作用,验证了该方法在提升伺服系统瞬态性能中的有效性。
5 结 论
通过改进深度强化学习算法,建立伺服系统瞬态性能优化方法,针对伺服系统特点,即运行存在时滞性、欠阻尼系统存在超调的问题,设计奖励函数,利用A3C优化算法,得到优化补偿函数。结合伺服系统仿真模型进行优化仿真,并在西门子数控系统中验证了优化效果。结果表明,在没有引入超调量的前提下对伺服系统的响应时间产生了明显的提升。由于本文方法具有易实施的特点,在优化控制领域中将具有良好的发展潜力。

