考虑几何非线性的钢管混凝土拱桥徐变效应研究

于 翔¹，曹明辉²，谭建平¹

（1、长沙理工大学土木工程学院 长沙410114；2、中国建筑第五工程局有限公司 长沙410004）

0 概述

结构的变形是一个动态的平衡过程，结构实际发生的大转动、大变形效应，使得结构变形不能单纯依靠线性方程进行求解，需在几何方程中添加位移二次项式。一部分学者通过龄期调整有效模量法将混凝土的徐变效应与混凝土弹性模量相结合，以此考虑结构几何非线性与徐变效应［1］。该法在短期徐变分析中精度较高，考虑结构荷载长期作用下徐变效应时就存在较为明显的误差，而且几何非线性的变形与徐变变形应当是互相影响，不断迭代，最后达到动态平衡的过程，如果将其作为一个整体来分析计算，则会产生相应偏差［2］。另一部分学者通过推导考虑几何非线性的结构变形平衡方程，自编程序对其进行分析，在计算精度与效率方面较为符合工程需要［3］。

1 平面梁单元几何非线性理论

杆单元在不同时刻的变形可以用图1 表示，其中XY为全局结构坐标系，指向始终一致。引入共旋坐标系作为局部的单元坐标系，该坐标系随时刻发生的变形而改变，并且始终以单元i节点指向j节点为x轴，y轴为x轴逆时针旋转90°而成［4-7］。

初始时刻单元在全局坐标系中坐标分别为（xi，yi）和（xj，yj），计算时刻t梁单元总位移在全局坐标系中表示为d=［ui vi θ i uj vj θ j］T，共旋坐标系下的单元坐标系中表示为dl=［ui'vi'θi'uj'vj'θj'］T。其中u、v、θ分别表示节点水平位移、竖向位移、转角位移。单元变形前后情况如图1所示。

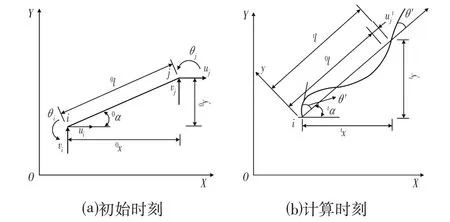
图1 不同时刻梁单元Fig.1 Beam Element at Different Time

共旋法的局部坐标下平面梁单元各节点位移可简化为：

式中：0l为初始时刻梁单元长度；tl为计算时刻t梁单元长度。其计算公式为：

式中：EA为抗压刚度；EI为抗弯刚度。

平面梁单元在大位移、小应变的几何非线性下的切线刚度矩阵Kt为：

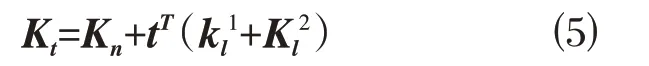
式中具体表达式由文献［7］推导给出。

2 初应变法计算徐变效应

共旋坐标系下单元的应变位移关系无需考虑非线性项，即：

式中：εe为节点位移产生的弹性应变矩阵；B0为线性应变矩阵。

考虑初应变的共旋单元坐标系下应力可表示为：

式中：ε0为混凝土徐变引起的初应变；D为应力矩阵。混凝土线性徐变应变εc表达式为：

几何非线性下徐变效应的分析是在叠加原理条件下在每一个时刻中进行迭代，直到其迭代精度达到要求后才会执行下一时刻的计算。邓继华等人［8］推导得出tn➝tn+1时段内，应变增量△εn+1c与应力增量△σ i表达式为：

由计算原理可明显得出：

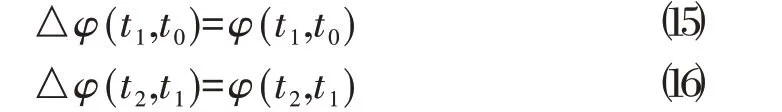
经推导后的递推公式可得出：

当n=0时：

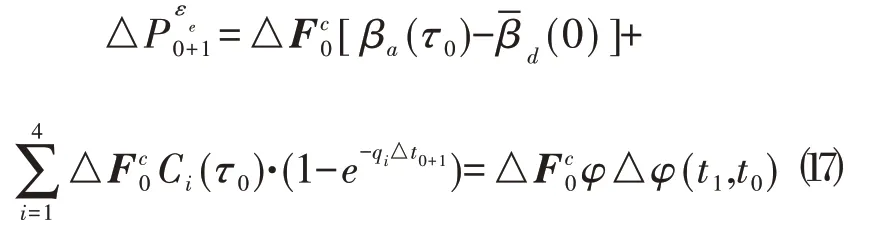
当n=1时：

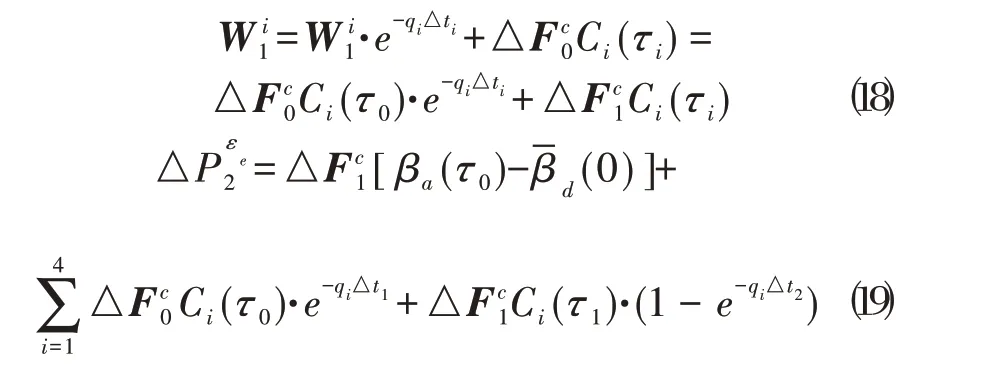
常规方法和递推公式都可得出如下公式：

3 算例

3.1 有限元模型对比

本文采用工程实例为湖南省南县的某大桥，以此建模并展开相应计算分析。该大桥为主跨368 m的大跨度自锚中承式钢管混凝土系杆拱桥，主桥跨径组合为（80+368+80）m。主跨线形为悬链线拱轴线，m=1.543，计算跨径L=356 m，计算矢高71.2 m，矢跨比为1∕5。利用ANSYS 中BEAM3 单元将三维立体的模型压缩成平面梁单元的茅草街模型，且数据与BEAM188 基本无异。然后通过格式化输出模型数据，导入以Fortran汇编了可分析几何非线性与徐变共同作用的程序。

整个模型共分为94 个节点，307 个单元。将空间模型压缩成平面模型，BEAM3 单元不支持蠕变功能，因此以BEAM3 单元自重作用下是否考虑几何非线性的跨中挠度为基准进行核对，以保证整个计算的说服性。具体如图2、表1所示。

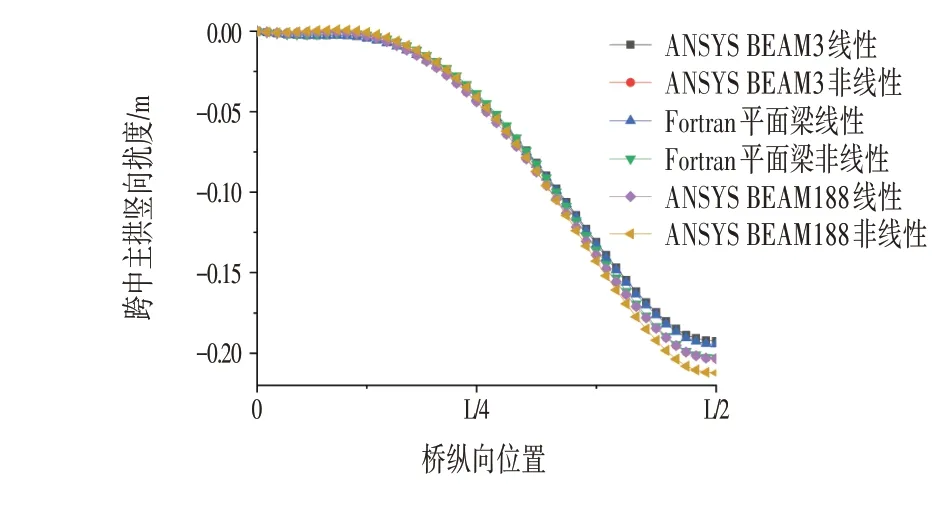
图2 不同单元计算的挠度Fig.2 The Maximum Deflection of Midspan Calculated by Different Software，Element Type and Calculation Method （cm）

表1 不同软件、单元类型、计算方式所计算的跨中最大挠度Tab.1 The Maximum Deflection of Midspan Calculated by Different Software，Element Type and Calculation Method （cm）

由图2 和表1 可知，ANSYS 与Fortran 平面梁单元计算结果差值1%以内，说明本文采用共旋坐标法的计算精度足以支撑整个计算。以Fortran 平面梁与ANSYS 空间梁BEAM188 的计算结果计算误差5%左右，后续计算徐变效应分析时将以BEAM188 计算数据作为参为依据，以加强数据的说服性。

3.2 误差对比

采用文献［10］中时步划分方法，以对数形式将1000d计算龄期划分为20个时步。初始加载龄期为10 d。

图3 和表2 显示2 种计算不同软件、不同单元类型、不同徐变分析模式计算下的差值从自重静力分析下的4.45%最终趋于0.61%的差值，此间差异是越来越小的。整个误差是正常的迭代误差，从数据层面上是可以说明Fortran 自编程徐变效应计算程序具有说服性。

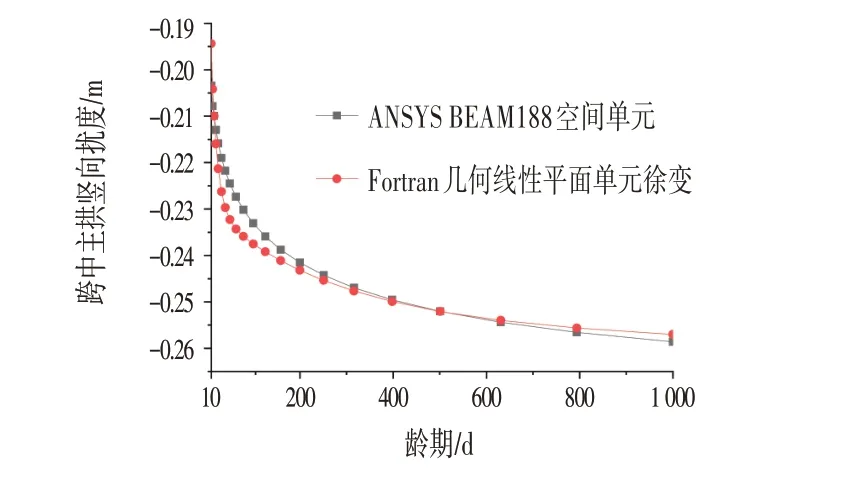
图3 ANSYS与Fortran不同龄期跨中拱顶竖向挠度徐变比对Fig.3 Comparison of Vertical Deflection and Creep of Mid Span Vault in Different Ages between ANSYS and Fortran （cm）

表2 ANSYS与Fortran不同龄期跨中拱顶竖向挠度徐变比对Tab.2 Comparison of Vertical Deflection and Creep of Mid Span Vault in Different Ages between ANSYS and Fortran （cm）

3.3 差异分析

在原有是否考虑几何非线性的自重作用下计算分析基础上，增加了是否考虑几何非线性与徐变效应的双重非线性数值计算。并比较四者的竖向挠度，寻找并发现差异所在（见图4、表3）。

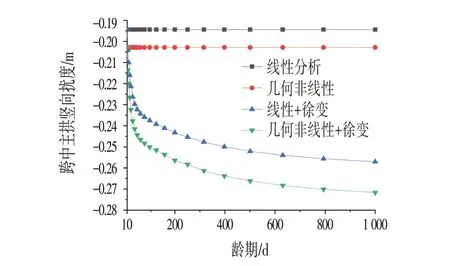
图4 各龄期下跨中拱顶竖向挠度Fig.4 Vertical Deflection of Middle Span Vault at Different Ages

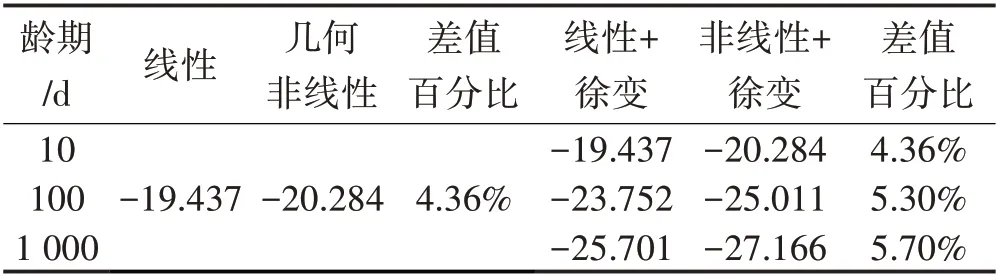
表3 4种计算方式下跨中拱顶竖向挠度比Tab.3 Vertical Deflection Ratio of Mid Span Vault under Four Calculation Methods （cm）

不考虑徐变的挠度与轴力不随龄期的发生而变化。随着龄期的增长，徐变速率由最初的急剧增长之后趋于平缓，同时钢管应力随着龄期的增长而增长，同时混凝土应力在徐变效应的影响下开始下降。

4 结论

通过基于共旋法推导了可考虑大变形、转动的平面梁单元的切线刚度矩阵，并在此基础上将徐变效应以初应变法作为等效节点荷载施加于梁上。以某大桥为实例建模，在ANSYA 建模基础上压缩为平面模型，并进行格式化输出，并将Fortran自编程序与ANSYS对比，以保证数据准确性与说服性。结论如下：

⑴将ANSYS 建成的BEAM188 空间模型转换成BEAM3 平面模型，并将关键数据格式化输出，导入Fortran自编程序。并与Fortran计算结果相比较，保证了计算精确性。

⑵以对数形式将1 000 d 计算龄期划分为20 个时步进行考虑，对自编程序进行了是否考虑几何非线性的徐变效应分析。结果发现，考虑几何非线性较之线性下的徐变分析而言，其数值相对于自重作用下的数值差异为5%左右。当计算荷载更为庞大、跨径更大等情况下，结构非线性更为明显，其双重非线性考虑则更有必要。