基于发展学生学科核心素养的物理教学实践研究

吴理 陆骅

摘 要：文章结合物理核心素养理念，探讨在教学实践中采用多种思路创设情境的方式方法，结合课堂内、外的教学情境研究如何引导学生发散思维，并在此基础上为培养学生的创新能力发展的教学研究提供有益的见解和实施策略。

关键词：创设情境;发善思维;创新能力

当前，以关注学生核心素养为核心的新课程改革正深入展开，而物理学科核心素养是学生在接受物理教育过程中逐步形成的适应个人终身发展和社会发展需要的必备品格和关键能力，是学生通过物理学习内化的带有物理学科特性的品质，是学生科学素养的关键成分;它包括物理观念、科学思维、实验探究和科学态度与责任。关注核心素养的培养就必然会进一步注重创新精神的培养，创新来源于问题，质疑是创新学习的重要环节，只有当学习者能质疑、会质疑，才有创新的可能，因此，质疑是创新的基础。物理课堂教学就是一个不断地引出问题、分析问题和解决问题的过程，同时也是学生思维展示的过程。孔子曾说过：“学而不思则罔。”明确告诉我们只读书而不思考，就等于没有读书。这句至理名言深刻地揭示了思维与学习的辩证关系。运用发散思维就是让学生进行“思维与灵魂的对话”，它不仅能够挖掘学生深层的智慧，而且也是培养学生创造能力的有效途径。实践中使我们深深体会到“纸上得来终觉浅，心中悟出方知深”的道理。培养和造就无数有灵气、会学习、有创新能力的人才，是教育改革的目标，那么引导学生学会科学的思维方法，不断地挖掘自身的创造潜能，提高学生的学习质量、科学文化素质和创新能力，也是我们当前首要任务和重大课题。

本课题是在我校推行“生态型学校课堂建设的研究与实践”的模式下进行物理课堂教学的探索与实践，是符合新课程上海新课程改革关于课堂教学改革的思想。实践是在课堂和谐的氛围下进行的，坚持以教师为主导、学生为主体，引导学生进行“发散思维”，强化课堂上学生思考问题的多向性、变通性、流畅性和独特性，即思考问题注重多思路、多方案，解决问题注重多途径、多方式，探索事物及其发展深层的信息，激发学生的创造潜能，创造出解决问题思路和方法。

一、 发散思维利于学生物理学科核心素养的培养

美国心理学家吉尔福特说：“人的创造力主要依靠发散思维。”发散思维的基础是思考，但它是高于思考问题的一种思维方式，是对给出的材料、信息从不同角度，向不同方向，用不同方法或途径探索新知识或寻求问题的多个答案的一种思维方式，是创造性思维的主要形式，也是高考物理要求的八种能力的一个集合。回顾物理学中重要规律的发现，如牛顿运动定律、电磁感应、相对论等，哪一个不是科学家发散思维的结果。如果说科学家具有发散思维能力的话，那么我们来看科学家出的题目：一位科学家涂了一条黑线条，让他的儿子不能擦掉，不能遮盖来把线条变细。他的儿子经过一番思考后，就在原来线条的旁边画出了一根同样的粗线条。这位科学家感到由衷的高兴。

发散思维就是求异思维，在求异中进行思维的扩散、思维的开放，也就是从一点出发沿着多方向达到思维目标，它是从一个知识点出发通过横向思维、逆向思维等建立与多个知识点的联系的方法。发散思维是不受已有知识的束缚，不受已有经验的影响，从各个不同的乃至不合乎常规思路去思考问题，采用探索、转化、变换迁移以及变形、组合、分解等手法增强学生思维的灵活性、拓展性，甚至可以让学生异想天开。这样不仅可以激发学生学习积极性，发挥学生的潜能，还能够达到培养学生的创造性思维，提高学生的物理学科核心素养。

二、 物理学科发散思维的类型

教学中本人从以下几个方面注重了学生发散思维的培养，虽然不够全面，但仍在探索中。

1. 题型发散是指将典型问题通过转换情景而变换成另一个类似的题目的一种思维。

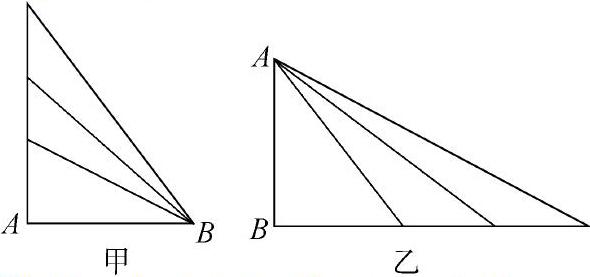
例1 如图所示，甲、乙是AB边长的相等的一系列光滑斜面，现有一个质量为m的小物体分别从不同的斜面顶端由静止开始滑下，试讨论物体下滑时间与斜面倾角的关系。

（把握住不变的边长，处理方法相似。）

2. 解法发散是一题多解、一题多问、一题多答或指多题一解来进行变通训练的一种思维。

例2 质量为m的物体，静止在粗糙的水平面上，在水平力F的作用下通过了位移s后撤去

F，物体继续向前滑行2s后停下来，求物体与水平面间的动摩擦因数。（先由学生讨论，教师点拨。三种解法，牛頓第二定律、动能定理和图像法。）

再如下图所示，三个完全相同的金属小球的质量均为m，已知三个小球都处于静止，且C球带有正电荷，求下图（1）、（2）、（3）中，绳OA对球的拉力、竖直挡板对小球的作用力及C球受到的电场力。（三题一解）

3. 过程发散是指由条件至目标或对物理过程进行的一种逆向思维。

例3 再如一个小球从固定斜面的底端，以某初速度沿着斜面向上运动3s到达最高点，求小球在第1 s、第2s、第3s内通过的距离之比。（匀减速直线运动的逆向可以看作初速度为零的匀加速直线运动的过程，则根据学过的知识可得到S1∶S2∶S3=5∶3∶1。）

4. 迁移发散是指利用函数式及图像在数学学科中与物理学中的不同含义来进行对比的一种思维形式，同时把物理中的公式、定理、定律和方法巧妙地迁移到数学或其他学科中去，达到化难为易的一种思维。

例4 甲、乙两辆汽车相距为S，沿着笔直的公路向同一方向运动，乙在甲的前面，且作初速度为零加速度为a的匀加速直线运动，甲以速度v作匀速直线运动，则甲、乙两辆汽车能相遇两次的条件是什么？（由运动规律可得，S=Vt―12at2，在数学中，t若有两个实数解，则需要根的判别式Δ>0，对于物理问题，若要相遇两次，也需要Δ>0，这样物理问题就在和数学问题的对比中解决了。）

5. 分解发散是指将一个复杂的命题分解成几个较为简单的命题，并逐一加以解决，然后再综合到一起进行解题的一种思维。例如：