流体饱和半空间二维地形三分量弹性波散射间接边界元模拟

梁建文， 吴孟桃， 巴振宁*

1 天津大学水利工程仿真与安全国家重点实验室， 天津 300350 2 天津大学土木工程系， 天津 300350

0 引言

震害调查和强震观测表明：局部地形(如凹陷、沉积和凸起)显著影响地震动的幅值及空间分布(张建毅等, 2012).而近年来，众多超高复杂建筑、重大交通工程和大型水利设施等不断出现，这些位于场地条件复杂地区的防震减灾工作亟需精确可靠的地震动参数.因此开展场地地震动局部地形效应研究具有重要的理论价值和巨大的社会效应.

局部场地地震效应，实质上是场地对弹性波的散射问题，近40年来，引起了国内外学者的重点关注.研究手段主要包括波函数展开解析解(Lee, 1984；袁晓铭和廖振鹏, 1993)和各种数值求解方法，例如有限元法(景立平等, 2005；宋贞霞和丁海平, 2013)、有限差分法(廖振鹏等, 1981；Zhang and Chen, 2006)、谱单元法(Komatitsch et al., 2004；周红等, 2010)、边界元法(Fu and Wu, 2001；Ge et al., 2005；梁建文和巴振宁, 2007)、广义R/T递推传播矩阵法(Chen, 1990, 1995；Ge and Chen, 2007)、离散波数法(Bouchon et al., 1989；Fu and Bouchon, 2004)和各种逼近方法(Fu, 2005；Hu et al., 2009；Yu et al., 2010； 管西竹等, 2011；Yu and Fu, 2012, 2014；陈高祥等, 2017).

从地形散射机理来看，依据入射波方向与地形轴线的关系可分为二维散射(入射波场与地形垂直)和三维散射(入射波场与地形不垂直).前者自Trifunac(1971)开创性地给出半圆凹陷地形对均匀半空间SH波的散射后，Wong和Jennings(1975)、Sánchez-Sesma和Campillo(1991)、Yuan和Men(1992)、杜修力和熊建国(1993)、刘晶波(1996)、Fu和Wu(2001)、Fu等(2002)、李伟华和赵成刚(2004)、梁建文等(2006)、Tsaur(2011)、Gao等(2012)、陈少林等(2014)、Lee和Liu(2014)、巴振宁等(2017)、Shyu等(2018)、高玉峰(2019)等相继对常规局部地形地震散射影响进行了大量深入研究.相对于二维散射，地形对三维地震波散射的研究成果还较少，主要有Sánchez-Sesma等(1983)、Mossessian和Dravinski(1989)、Sánchez-Sesma和Luzón(1995)、Chávez-García(2003)、赵成刚和韩铮(2007)、梁建文等(2014)、王铭锋等(2017)、Ba和An(2019)等采用各类方法求解了均匀或层状半空间中局部地形的三维响应问题，获得了二维模型无法反映的复杂场地三维动力响应特征.三维模型与二维相比有着本质差别，能够全面反映地震动的空间分布特征，但对计算内存需求大、求解耗时长，尤其对于时域响应解.

在不失一般性的情况下，建立二维地形的三分量散射模型(即2.5维模型)是一种计算量远小于三维，并能在一定程度上反映场地三维动力响应特征的有效方法.Pedersen等(1994)采用基本解为全空间格林函数的间接边界元方法(IBEM)研究了二维沉积谷地的三维散射问题，但该方法需要离散自由地表.Stamos和Beskos(1996)采用直接边界元方法(DBEM)求解了二维凹陷地形的三分量弹性波散射，其解也仅适用于均匀半空间情况.Ba和Liang(2010a, b)采用基本解为半空间格林函数的IBEM求解了层状半空间凹陷地形的2.5维散射问题.以上研究仅限于单相介质，而实际地表土层很多是饱和多孔介质，尤其是滨海地区的沉积谷地中沉积层多为饱和土.根据Biot理论(Biot, 1956)，波在流体饱和介质中的传播与弹性介质中的传播特征截然不同.目前关于流体饱和半空间二维地形的三维地震散射问题研究，仍鲜有报道.

本文将Ba和Liang(2010a,b)给出的方法进一步拓展到层状流体饱和半空间情况，推导建立了饱和土层及下卧基岩的三维精确动力刚度矩阵和移动线源下的动力格林函数，进而求解了流体饱和半空间中二维地形三分量弹性波散射问题.文中通过与已发表结果的比较验证了方法的可靠性和求解精度，并以梯形凹陷和半椭圆沉积地形为算例，在空间域内给出了一些时频数值结果，以期为揭示层状介质中局部地形地震波的三维散射机理提供一定参考.

1 理论模型及求解

如图1所示，流体饱和层状场地中存在一无限长任意截面形状局部地形，场地模型由水平成层的饱和土及其下的基岩半空间组成，局部地形与土层的交界面为S.地震体波(P、SV或SH波)由下卧面入射，入射波波阵面的法向量在水平面上的投影与y轴的夹角为θh(水平入射角)，在竖直面内与z轴的夹角为θv(竖向入射角).

图1 流体饱和半空间二维地形三分量弹性波散射模型示意图Fig.1 Sketch of three-component scattering of elastic waves by 2-D topography in a fluid-saturated half-space

由于弹性波斜入射下，半空间中局部地形沿其y轴的两个相邻截面的响应只存在相位差(因截面位置不同产生)，那么可仅选取任一截面进行离散和求解，然后通过沿地形轴向的波数拓展求得其他截面位置的动力响应.本文采用以移动斜线荷载(孔隙水压)动力格林函数为基本解的2.5维IBEM进行问题求解.具体求解时，通过波场分离将整体模型分解为开口的层状半空间(波场1)和闭合的局部地形(波场2)，并假定波场1中存在着自由波场和散射波场，波场2中仅存在散射波场.首先提出层状饱和场地自由波场(无地形存在)求解的精确动力刚度矩阵方法，然后通过在各离散斜线单元上施加一组沿轴线方向(y轴)移动的三坐标方向虚拟均布荷载和虚拟孔隙水压，求解位移和应力的格林影响函数来模拟散射波场.虚拟移动均布荷载和孔隙水压的密度，可通自由地表和地形的边界条件(位移、应力连续条件和透水条件)求得.对于时域响应则可通过对频域结果进行快速Fourier逆变换得到.

1.1 Biot理论及其一般解

根据文献(Biot, 1962)，流体饱和多孔介质体系的土体本构方程和渗流连续方程可表示为

σij=λ*eδij+2μ*εij-αδijpf,

(1a)

-pf=αMe+Mξ,

(1b)

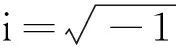
以土骨架位移U和流体相对位移w表示的饱和土动力控制方程为

(2a)

(2b)

其中，ρ=(1-n)ρs+nρf，n为孔隙率，ρ、ρs和ρf分别为两相土、土骨架和流体的质量密度；b、m、α和M均为饱和相关参数.

函数f(x,y,z,t)对时间t以及水平坐标x和y的Fourier变换及其逆变换可表示为

(3a)

f(x,y,z)=

(3b)

其中，上标“=”表示对空间分量(x,y)的Fourier变换，上标“～”表示对时间t的Fourier变换.对式(2)进行式(3a)的Fourier变换并进行求解，可得到土骨架位移以及流体相对位移在频率-波数域中解为

-kSzkxβ(ASVeikSzz-BSVe-ikSzz)-kyβ(ASHeikSzz+BSHe-ikSzz),

(4a)

-kSzkyβ(ASVeikSzz-BSVe-ikSzz)+kxβ(ASHeikSzz+ASHe-ikSzz),

(4b)

-(ASVeikSzz+BSVe-ikSzz)/β,

(4c)

-D3(ASVeikSzz+BSVe-ikSzz)/β,

(4d)

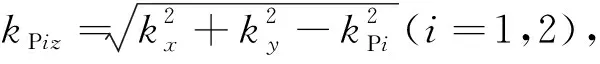
D3=ρfω2/(ibω-mω2)，AP1、BP1、AP2、BP2、ASV、BSV、ASH和BSH分别为上行和下行P1、P2、SV和SH波的幅值.kP1、kP2和kS分别为P1、P2和S波的波数，可由下式确定：

(5)

其中，

β1=[(mω2-ibω)(λ*+2μ*+αM)+ρω2M

-2αω2MρfB]/[M(λ*+2μ*)],

(6a)

(6b)

1.2 饱和介质三维精确动力刚度矩阵及自由波场求解

考虑上行和下行的波幅值，每一饱和土层上下表面处的土骨架位移和流体相对于土骨架位移可由式(7a)表示.结合式(1)和式(4)，同时令饱和土层上表面处的外力

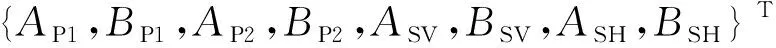
(7a)

[S]{AP1,BP1,AP2,BP2,ASV,BSV,ASH,BSH}T,

(7b)

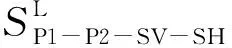
(8)

(9)

1.3 移动线荷载(孔隙水压)动力格林函数及散射波场模拟

流体饱和半空间层内部作用的移动斜线荷载(孔隙水压)如图2所示，荷载作用层厚度为d，px0、py0和pz0分别为沿坐标x、y和z方向的外荷载幅值，pf0为孔隙水压幅值.该移动线源在时间-空间域中展开形式为：

p(x,y,z,t)=p0δ(z-xtanθ)δ(y-ct),

(10)

(11)

如图2，在节点1、2处引入附加交界面以使荷载作用介质层固定，总响应涉及的特解、齐解和反力解可由直接刚度法方便求得.流体饱和半空间动力格林函数的详细推导过程可参考层状弹性介质的思路(Ba and Liang, 2010a)，不再赘述.

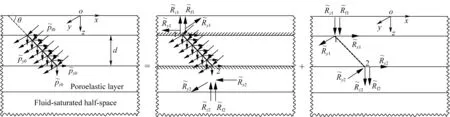
图2 流体饱和层中移动斜线均布荷载(孔隙水压)Fig.2 Moving distributed forces (pore pressure) acting on an inclined line in fluid-saturated layers

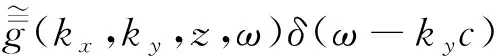
×exp(iωt-ikxx-ikyy)dkxdky

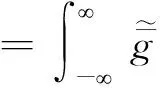
(12)

利用该基本解，我们得到散射波场在地形边界S各单元上产生的土骨架位移以及流体相对位移、应力和孔隙水压计算公式为

(13a)

(13b)

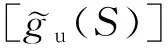
1.4 边界条件及求解

求解中涉及到的边界条件，按地形类型可分为：(1)零应力边界条件；(2)位移和应力连续边界条件.按是否透水则有：(a)排水边界(透水情况)；(b)不排水边界(不透水情况).注意到，对于透水情况，孔隙流体自由流动，孔隙水压为零；对于不透水情况，孔隙流体无法自由流动，流体较土骨架的相对位移为零.而无论是否透水，求解步骤均相同，以下给出一般性边界条件：

(1)零应力边界条件(如凹陷地形，以“Sc”表示)

(14)

其中[W(s)]为权函数，一般取为单位矩阵.将式(13)代入式(14)得：

(15)

其中，

(16a)

(16b)

(2)位移和应力连续边界条件(如沉积地形，以“Sv”表示)

(17a)

(17b)

同样，将式(13)代入式(17)得：

(18a)

(18b)

其中，

(19a)

(19b)

(19c)

(19d)

求解式(15)和(18)，可得层状饱和半空间中局部地形附近地表任意位置的位移和应力(孔隙水压)幅值，对于时域动力响应可通过快速Fourier逆变换求得.

2 退化验证和精度比较

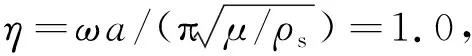
图3 本文结果与Liang等(2006)给出结果的比较Fig.3 Comparison of the solutions given by the present study and Liang et al.(2006)

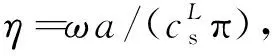
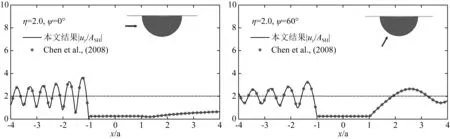
图4 本文结果与Chen 等(2008)给出结果的比较Fig.4 Comparison of the solutions given by the present study and Chen et al.(2008)

de Barros和Luco(1995)采用边界积分方程法首次给出弹性半空间中二维半圆沉积谷地三分量弹性波散射结果的数值解.在本文方法退化为单相介质情况的基础上，分别以均匀地形和层状地形对P波散射的求解模型为例，图5比较了本文方法和文献方法求得的三个坐标方向地表位移幅值在不同斜入射角度下的计算结果.相关参数取值如下：αv=2βv=βL，αL=2βL，αR=2βR=4βL，ρv=(2/3)ρL，ρR=(4/3)ρL，ζR=ζL=ζv=0.005，其中α和β分别为压缩波波速和剪切波波速，上标“v”、“L”和“R”分别表示与沉积内、沉积外和下卧基岩有关的变量.无量纲频率取为η=ωa/πβL=0.5，地震波入射角度取为θh=0°和θv=30°.由图5可见，无论在均匀介质还是在层状介质中，两种方法的计算结果均具有良好的一致性，较好地验证了本文方法的求解精度.

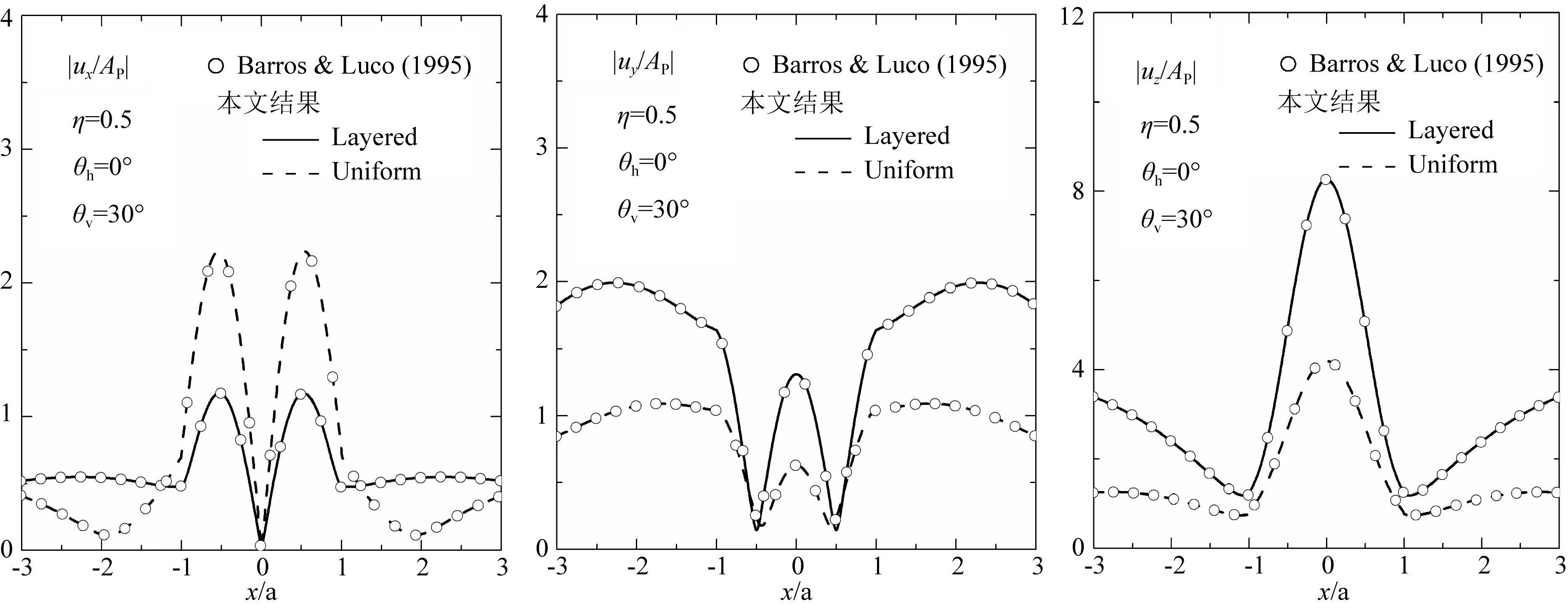
图5 本文结果与De Barros和Luco(1995)给出结果的比较Fig.5 Comparison of the solutions given by the present study and Barros & Luco (1995)

3 数值算例

3.1 凹陷地形对弹性波的三维散射

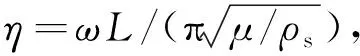
图6 地表透水时梯形凹陷附近的孔压变化(a) 透水：η=0.5, n=0.3, θh=0°, θv=30°; (b) 透水：η=0.5, n=0.3, θh=90°, θv=30°; (c) 透水：η=1.0, n=0.3, θh=0°, θv=30°; (d) 透水：η=1.0, n=0.3, θh=90°, θv=30°; (e) 透水：η=2.0, n=0.3, θh=0°, θv=30°; (f) 透水：η=2.0, n=0.3, θh=90°, θv=30°.Fig.6 Variation of pore pressure near the trapezoidal canyon with drained condition

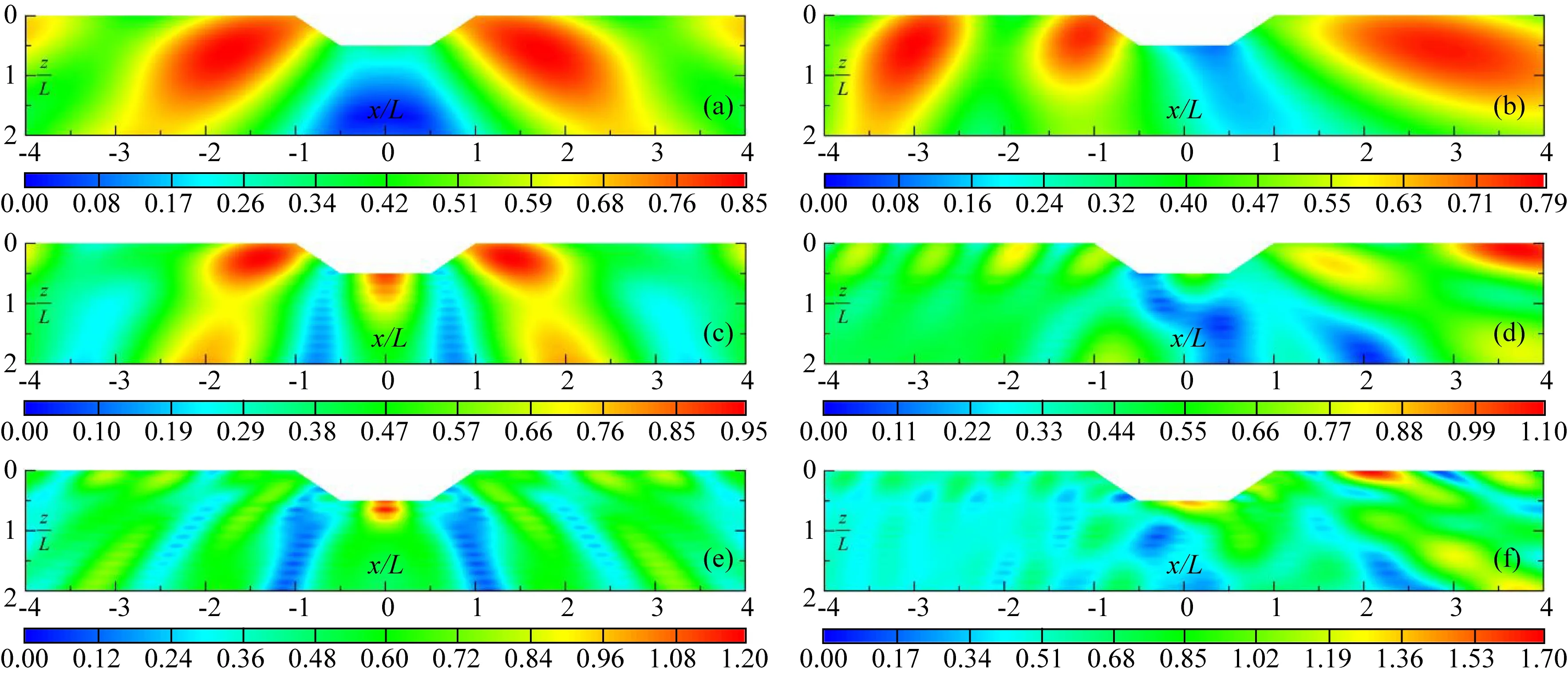
图7 地表不透水时梯形凹陷附近的孔压变化(a) 不透水：η=0.5, n=0.3, θh=0°, θv=30°; (b) 不透水：η=0.5, n=0.3, θh=90°, θv=30°; (c) 不透水：η=1.0, n=0.3, θh=0°, θv=30°; (d) 不透水：η=1.0 n=0.3, θh=90°, θv=30°; (e) 不透水：η=2.0, n=0.3, θh=0°, θv=30°; (f) 不透水：η=2.0, n=0.3, θh=90°, θv=30°.Fig.7 Variation of pore pressure near the trapezoidal canyon with undrained condition

结果显示，饱和排水情况(地表透水)和饱和不排水情况(地表不透水)的场地动力响应显著不同，且与入射波的频率、角度及观测点位置密切相关.总体上，饱和不排水时凹陷表面的孔隙水压幅值更大，原因在于孔隙流体的存在对波的传播有着耗能的作用，而随着观测点逐渐远离凹陷地形(x/a逐渐增大)，两者的幅值差异逐渐减小，地表是否透水的影响减弱.随着入射频率的增大，半空间中孔隙水压幅值的变化及分布逐渐变得复杂.η=0.5(较低)时，幅值响应主要由其自由波场决定，η=2.0(较高)时，起主导作用的则为凹陷地形引起的附加散射波场.随着水平入射角度的变化，凹陷周围土层孔隙水压幅值的空间分布变化较为明显.θh=0°时，孔隙水压幅值关于凹陷轴线对称，θh=90°时，孔隙水压幅值在波入射侧较大，且分布较为复杂.

表1 基岩上单一饱和土层中半椭圆沉积谷地材料参数Table 1 Material parameters of semi-elliptical alluvial valleys in a single saturated soil layer overlying the bedrock half-space

事实上，与经典的半圆和半椭圆凹陷地形相比(Wong and Jennings, 1975；袁晓铭和廖振鹏, 1993；Liang et al., 2006)，梯形凹陷的土层和地形放大效应研究还较少，本文仅给出了一个均匀凹陷三维散射问题的简单结果，后续可针对成层场地中更多复杂截面形状凹陷地形开展研究.已有结果表明，对于给定的入射频率和入射角度，层状饱和半空间中凹陷附近动力响应由层状场地自身的动力特性(成层场地自由波场)和凹陷截面形状(凹陷地形形成的散射波场)共同决定(巴振宁和梁建文, 2013)，而均匀饱和半空间情况仅取决于凹陷截面形状.因此为更为准确的确定凹陷地形附近的地震响应特征，需综合考虑凹陷附近的土层分布情况及其截面形状.

3.2 沉积地形对弹性波的三维散射

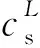
结果显示，沉积地形的存在(图中虚线位置)显著改变了饱和层状半空间中孔隙水压振幅的分布.对于入射P1波，孔隙水压幅值的空间分布十分依赖于竖向入射角θv，但对水平入射角θh相对不敏感，其幅值大小似乎随着竖向入射角的增大而逐渐增大.孔隙水压幅值的最大值出现在靠近谷地与土层交界面的右侧，这意味着这些区域具有较大的应变响应.当θv=90°(P1波垂直入射)时，幅值的分布关于谷地轴线对称，响应与水平角度无关.对于入射SV波，水平和竖向角度都对孔隙水压的变化(尤其是幅值)有着显著影响.比较图8和图9，可以明显看出SV波入射下谷地内部孔隙压力的空间分布更复杂，幅值也更大.其原因在于不同类型入射波幅值的差异主要是自由波场的差异，孔隙流体承担传递来的激励能量改变，孔隙水压自然不同.同样，当θv=90°(SV波垂直入射)时，幅值的分布具有对称性，这也为我们的结果提供了额外的信心.

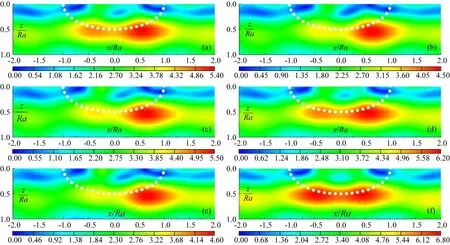
图8 P1波入射下半椭圆沉积附近的孔压变化(a) θv=45°, θh=30°； (b) θh=45°, θv=30°； (c) θv=45°, θh=60°； (d) θh=45°, θv=60°； (e) θv=45°, θh=90°； (f) θh=45°, θv=90°.Fig.8 Pore pressure amplitudes around the semi-elliptical valley under P1 waves incidence

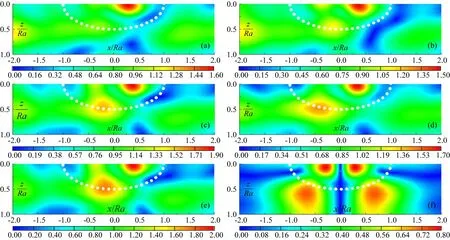
图9 SV波入射下半椭圆沉积附近的孔压变化(a) θv=45°, θh=30°； (b) θh=45°, θv=30°； ( c) θv=45°, θh=60°； (d) θh=45°, θv=60°； (e) θv=45°, θh=90°； (f) θh=45°, θv=90°.Fig.9 Pore pressure amplitudes around the semi-elliptical valley under SV waves incidence

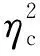
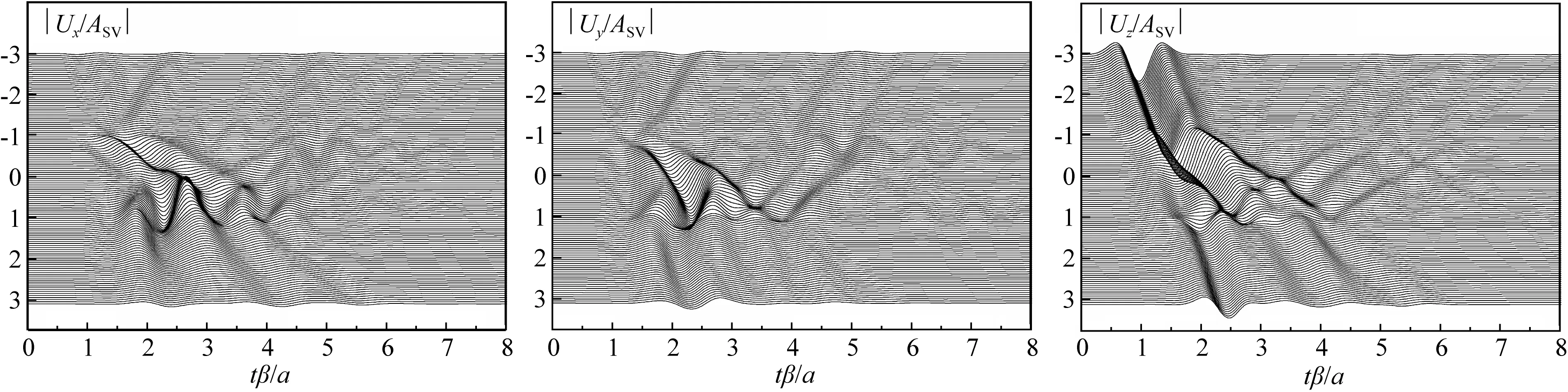
图10 均匀饱和半空间中沉积附近地表位移幅值时域结果Fig.10 Time domain solutions for surface displacement amplitude around the valley in a uniform half-space

图10展示了均匀半空间情况沉积附近地表位移时域响应，图中|Ux/ASV|、|Uy/ASV|和|Uz/ASV|分别表示三个坐标方向的无量纲位移.可以看到，沉积地形的存在使得谷地附近的位移幅值与自由波场(无沉积地形存在)存在明显差异，且由于局部不规则形成的反射波和散射波与入射波相互干涉，使得谷地附近位移幅值的持续时间明显长于自由波场情况.另外，SV波在整个半空间的传播过程在时域内可更为清楚的观察到，如谷地左侧(x/a≤-1.0)首先接收到直达波，随后接收到谷地左角点(x/a=-1.0)产生的散射波，最后接收到谷地右角点(x/a=1.0)产生的散射波.同时，入射波在较软的沉积介质中经过多次反射，导致谷地内部位移相较于外部的持续时间明显更长，且幅值更大.

4 结论

基于Biot理论，建立了层状多孔介质内部移动线荷载(孔隙水压)格林函数，进而提出了求解流体饱和半空间中二维局部地形三分量弹性波散射问题的间接边界元方法(IBEM).该方法优势在于离散仅限于地形边界(无须离散自由地表)，且格林函数计算不存在奇异性(荷载直接加在边界上)，因而计算精度容易控制，且对复杂边界条件具有很强的适应性.

文中以给出的方法具体研究了梯形凹陷地形和半椭圆沉积地形的三维地震效应，分别在频域和时域内进行了计算分析.频域结果表明，局部地形的存在显著改变了饱和层状半空间中孔隙水压的幅值及空间分布，且依赖于地震波类型、入射频率、入射角度和边界透水条件等影响因素.地形附近动力响应由半空间动力特性和地形截面形状共同决定.时域结果表明由于局部不规则形成的反射波和散射波与入射波相互干涉，使得地形附近位移幅值的持续时间明显长于自由波场情况.与均匀半空间相比，基岩的存在的位移时程的空间分布更为复杂，振动时长增加.层状半空间，土层自身特性(土层刚度、厚度等)对波的传播路径和持续时间有重要影响.

本文建立的以移动斜线荷载(孔隙水压)格林函数为基本解的IBEM在近地表复杂场地对地震波三维散射和土-结构相互作用方面有着重要应用前景.后续研究将进一步考虑有实际观测数据的场地，以期为区域地震危险性分析、烈度区划以及局部地形附近建筑物的抗震设防等工作提供一定理论基础.