含水平缝薄互层储层地震响应特征物理模拟

刘海浩， 丁拼搏* ， 李向阳

1 油气资源与探测国家重点实验室， 中国石油大学(北京)， 北京 102249 2 CNPC物探重点实验室， 中国石油大学(北京)， 北京 102249

0 引言

裂缝广泛存在于地下岩石中，是岩石中流体重要的储集空间和运移通道.特别是在油气勘探领域，裂缝对于油气藏的勘探与开发有着重要的意义.目前针对裂缝介质岩石物理建模(Hudson, 1981; Schoenberg and Sayers, 1995; Chapman, 2003; Li et al., 2020；林承焰等，2020)主要针对垂直定向排列的裂缝，相应的裂缝预测方法(尹志恒等, 2011; 李向阳和王九拴, 2016; Luo et al. 2017, 2020; Pan et al., 2017; Liu et al., 2018; Zhang et al., 2019；陈志刚等，2020；赖富强等，2020)也主要针对垂直定向排列裂缝.垂直裂缝模型对应于由构造运动产生的高角度裂缝，但在实际的储层中还存在着层理缝，这些裂缝沿着层理发育，展布方向近似平行于地层层理.通常在地层倾角较小的情况下，层理缝的空间展布近似水平(Swanson, 2007; 贺振建等, 2011; Cobbold et al., 2013; Luo et al., 2017; 朱维耀和马旭东, 2018; 李子宁, 2018).水平缝对储层特征有重要影响，对油气藏勘探开发也具有十分重要的意义.目前针对水平缝的研究多是从地质的角度出发，探讨其成因、发育规律、启闭机制等(Doolin and Mauldon, 2001; Laubach and Diaz-Tushman, 2009; 李子宁, 2018)，但是目前针对水平缝地震响应特征的研究较少.由于水平裂缝平行于地层层理，裂缝的地震响应与层理的地震响应互相混叠.特别是当水平缝发育于薄层或者薄互层储层中时，这种混叠会使地震波场极其复杂，这给水平裂缝的地震识别带来了巨大的困难.明确水平裂缝的地震响应特征，特别是在薄互层背景下水平裂缝的地震响应特征，对于含水平裂缝储层的勘探、开发具有重要的意义.

地震物理模拟是按照野外实际地质模型，选取合适的材料，按照一定的相似比制作物理模型，然后利用超声波或者激光超声波模拟实际野外地震勘探并得到相应的模拟地震记录.地震物理模拟能反映地震波的实际传播状态，所得到的结果相比于数值模拟而言，更接近于野外真实地震记录(Hilterman, 1970; French, 1974; 魏建新和狄帮让, 2006; Wong et al., 2009).地震物理模拟在观测系统设计及优化、地震成像、地震各向异性、储层预测、裂缝及流体识别等领域都发挥了重要的作用.例如Cheadle等(1991)利用物理模型资料讨论了正交各向异性介质的地震响应特征；Di等(2008)利用物理模拟方法讨论了宽、窄方位的三维地震采集对于砂体识别的影响；Wang等(2010)基于地震物理模拟手段讨论了流体替换在地震资料解释中的应用.在裂缝介质物理模拟方面，目前常用的裂缝模拟工艺主要有三种：有机玻璃薄片叠合法(Tatham et al., 1983, 1988; Johnson et al., 1989; Ebrom et al., 1990)、片状孔隙材料叠合法(Cheadle et al., 1991; 董良国等, 1999)以及嵌入式可控裂缝模拟方法(Ass′ad et al., 1992, 1993, 1996; Wei et al., 2008; Ding et al., 2014;丁拼搏等, 2015).这些裂缝模拟工艺都有其合理性，且在裂缝介质地震响应特征分析中发挥过重要作用.例如，Tatham等(1983, 1988)基于有机玻璃薄片叠合法模拟了裂缝介质，并详细讨论了裂缝密度与各向异性的关系，成功观测到了横波分裂现象.董良国等(1999)利用片状孔隙材料叠合法模拟了TI介质(Transverse Isotropy, 横向各向同性介质)，分析了其传播速度和反射波时差等特征.Ding等(2014, 2017, 2019, 2020)、丁拼搏等(2015)提出了一套可控裂缝人工岩样制作方法，并讨论了裂缝参数对地震波传播速度、各向异性等特征的影响.

本文利用地震物理模拟技术构建了含水平缝薄互层储层的物理模型，水平缝裂缝单元采用片状孔隙材料叠合法进行模拟，并在实验室条件下模拟采集了4条二维纵波测线的地震记录，利用开源软件Seismic Unix(美国科罗拉多矿院波场研究组CWP开发)和商业软件CXTOOL(英国地质调查局各向异性研究组EAP开发)对数据进行处理分析，获得了最终偏移剖面和叠前AVO道集.随后，对偏移结果和叠前AVO道集进行时频分析，获得了分频剖面及频变AVO响应曲线.时频分析方法采用了基于时频重排算法的平滑伪Wigner-Ville分布(Wu and Liu, 2009)，该方法适合于地震信号的时频分析，具有较高的时频聚集性和分辨率，可以较为准确的刻画地震信号的频率特征.基于此，本研究分析了含水平缝薄互层储层的频率特征及频变AVO特征.频变AVO反演方法最早由Wilson等(2009)提出，并将其应用于流体检测.随后，吴小羊(2010)进一步优化了频变AVO反演算法，并将其应用于北海地区流体检测；郭智奇等(2016)分析了非弹性层状介质的频变AVO响应特征；Qin等(2018)、秦喜林(2019)利用频变AVO反演方法，对缝洞储层进行流体检测；Alshangiti(2019)讨论了基于不同AVO近似公式的频变AVO反演结果.本研究通过对地震物理模拟数据的频变AVO分析，旨在验证频变AVO方法应用于含水平缝薄互层储层识别的可行性，为后续含水平缝薄互层储层识别提供支撑.

1 模型设计及制作

1.1 裂缝单元的设计及制作

在本研究中，首先预制了一系列的裂缝单元，然后将这些裂缝单元嵌入到物理模型中.裂缝单元是采用片状孔隙材料叠合法，首先利用孔隙材料制作若干薄片，然后将这些薄片粘合压实，粘合剂为环氧树脂和硅橡胶的混合物.制作裂缝单元前，首先按照设计好的尺寸制作模具；然后在模具中一片片地粘合片状孔隙材料薄片，薄片与薄片之间需要涂抹粘合剂，粘合剂的涂抹应当尽量均匀；最后对这些粘合的薄片进行压实固化，为了保证压实固结的质量，一块裂缝单元的制作可分若干次进行.此外，为减少裂缝单元边缘位置不光滑所带来的绕射波干扰，在整个裂缝单元制作完毕后，还需要将其边缘打磨光滑.裂缝单元制作完毕后，测量其相关参数如表1所示，图1所示为制作好的裂缝单元实物照片.

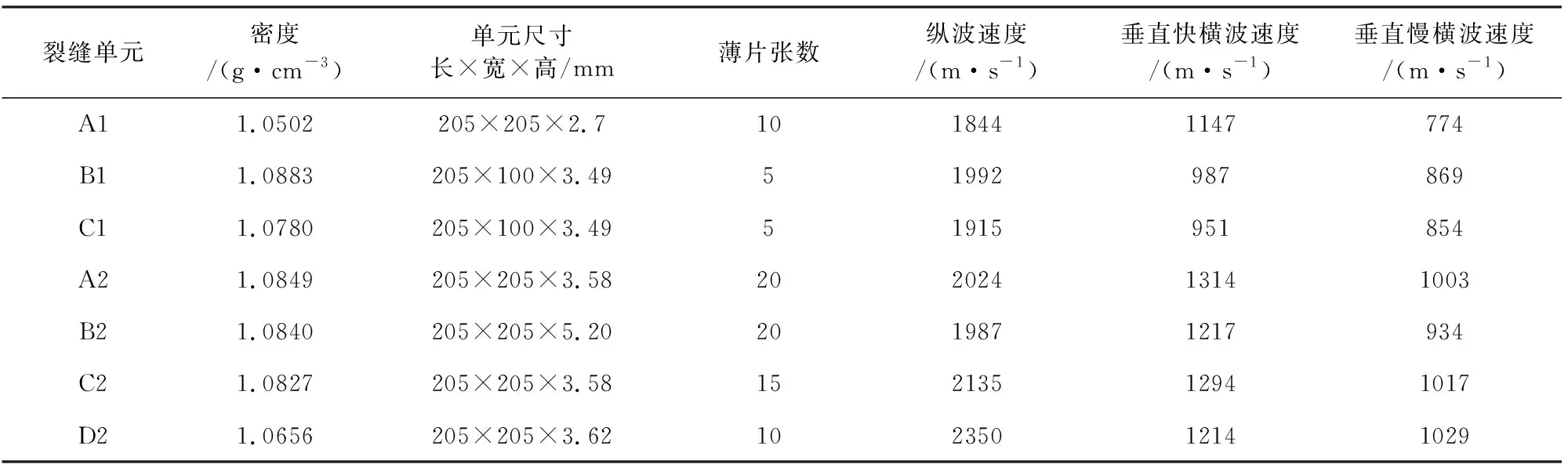
表1 各裂缝单元参数Table 1 Parameters of fracture elements

图1 裂缝单元实物照片Fig.1 Pictures of fracture elements

1.2 模型整体浇筑

本研究中，物理模型设计图如图2a所示.物理模型整体长、宽、高分别为800 mm、600 mm、134.6 mm.中间的目的层是由10套薄互层交互构成，在第2层和8层分别有裂缝单元镶嵌其中，如图2a中黑色箭头所示的位置，模型基底为高速层，盖层为低速度层.第2、8薄层中裂缝单元在横向上的位置和分布如图3和图4所示.将薄互层第2层记为裂缝层1，裂缝单元A1、B1、C1分布其中如图3所示；将薄互层第8层记为裂缝层2，裂缝单元A2、B2、C2、D2分布其中，其具体位置如图4所示.在模型制作过程中，按照由下而上顺序层层浇筑.基底和盖层分4次浇筑，每次浇筑的部分完全固结以后，再浇筑下一部分，以防止层位过厚会造成在固结过程中产生变形.地震物理模拟依据的是相似性原理，模型尺寸、传播速度以及地震波频率、信号采样率等参数均需设置一定的相似比，在本论文中，相似比定义为实验室物理模型相关参数与野外地质模型相关参数的比值.本研究中，尺寸相似比为1∶ 10000，即模型中的1 mm对应实际地质模型的10 m；此外，速度相似比为1∶ 1，即地震波在物理模型中的传播速度与在野外地质模型中的传播速度保持一致.表2中列出了物理模型中各层的厚度及其对应的地质模型厚度、以及纵横波速度和密度等参数.基于以上设定，与本研究中的物理模拟问题等效野外地震观测问题可以表述为：在长度为8000 m、宽度为6000 m的工区范围内，对地表以下1346 m范围内的地层进行地震勘探；各个地层地震波传播速度如表2所示；观测的重点是地层中某些位置发育的水平裂缝，水平裂缝发育的具体位置如图2、图3、图4所示，水平裂缝相关的参数如表1所示.

图2 (a) 物理模型垂向示意图; (b) 实物照片Fig.2 (a) Vertical schematic diagram of the physical mode; (b) Corresponding picture

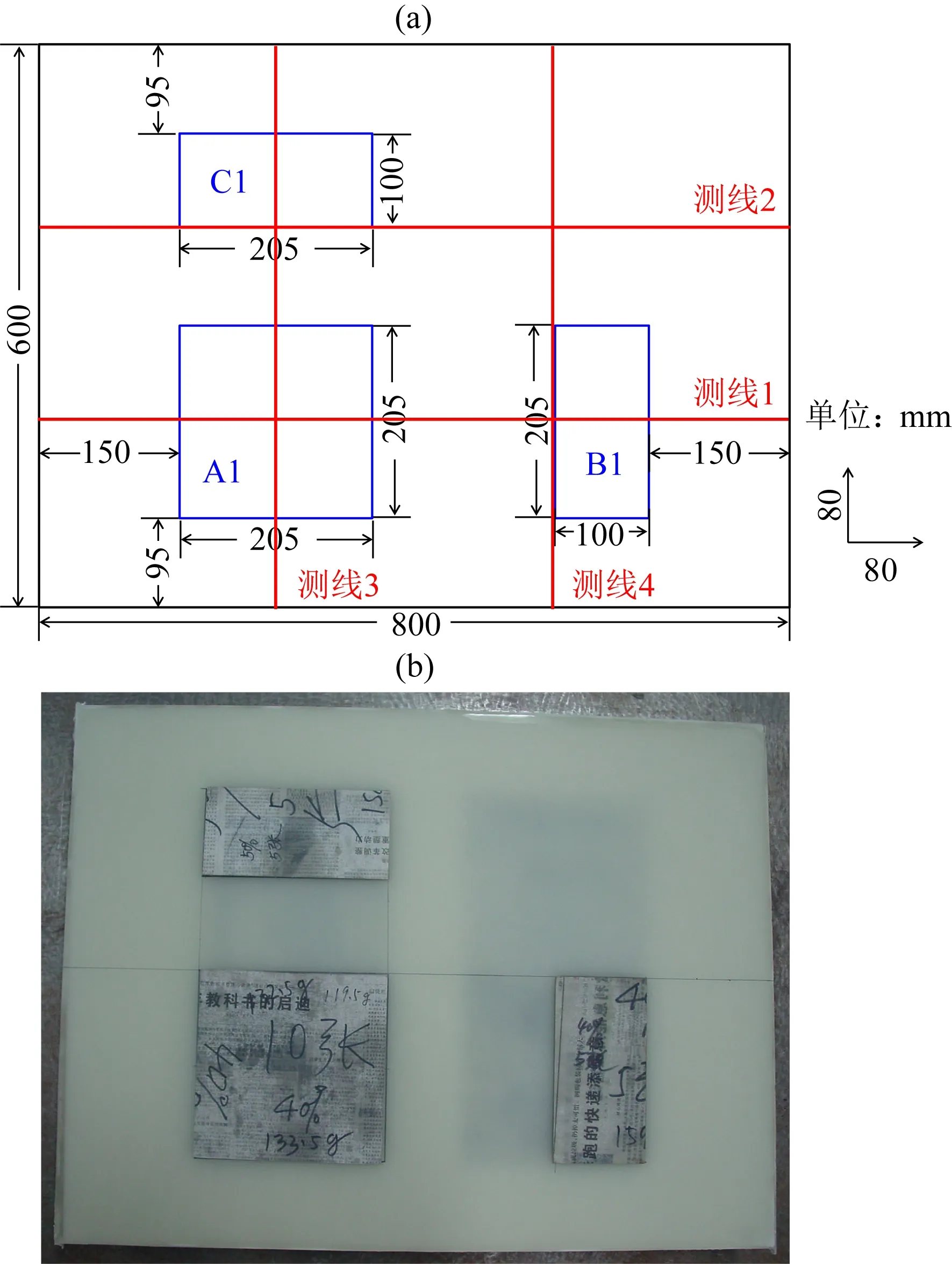
图3 裂缝单元横向分布(a) 裂缝层1(第2薄层); (b) 相应实物照片.Fig.3 Horizontal distribution of fracture elements(a) Schematic diagram of fracture layer 1 (thin layer 2); (b) Corresponding picture.

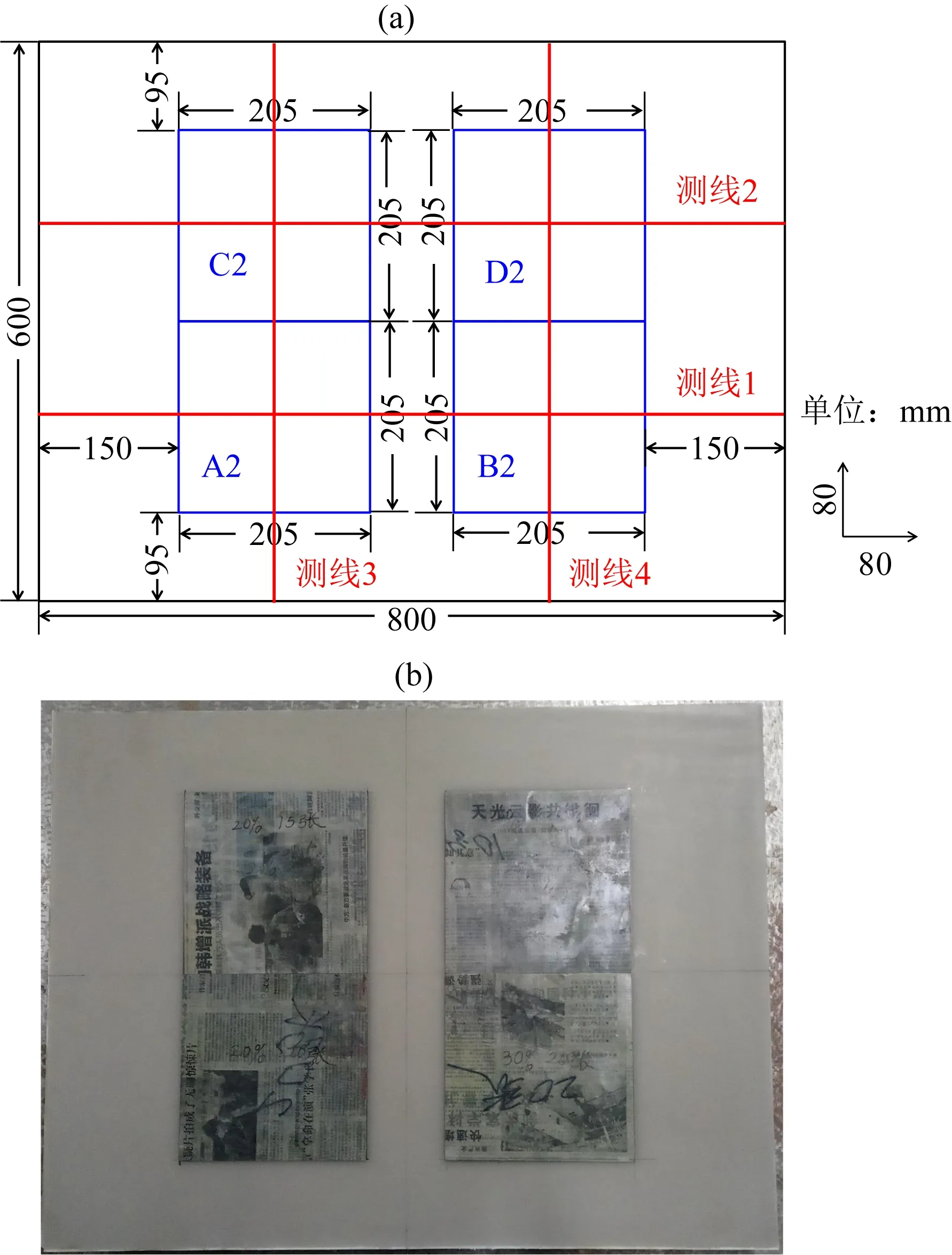
图4 裂缝单元横向分布(a) 裂缝层2(第8薄层); (b) 相应实物照片.Fig.4 Horizontal distribution of fracture elements(a) Schematic diagram of fracture layer 2 (thin layer 8); (b) Corresponding picture.

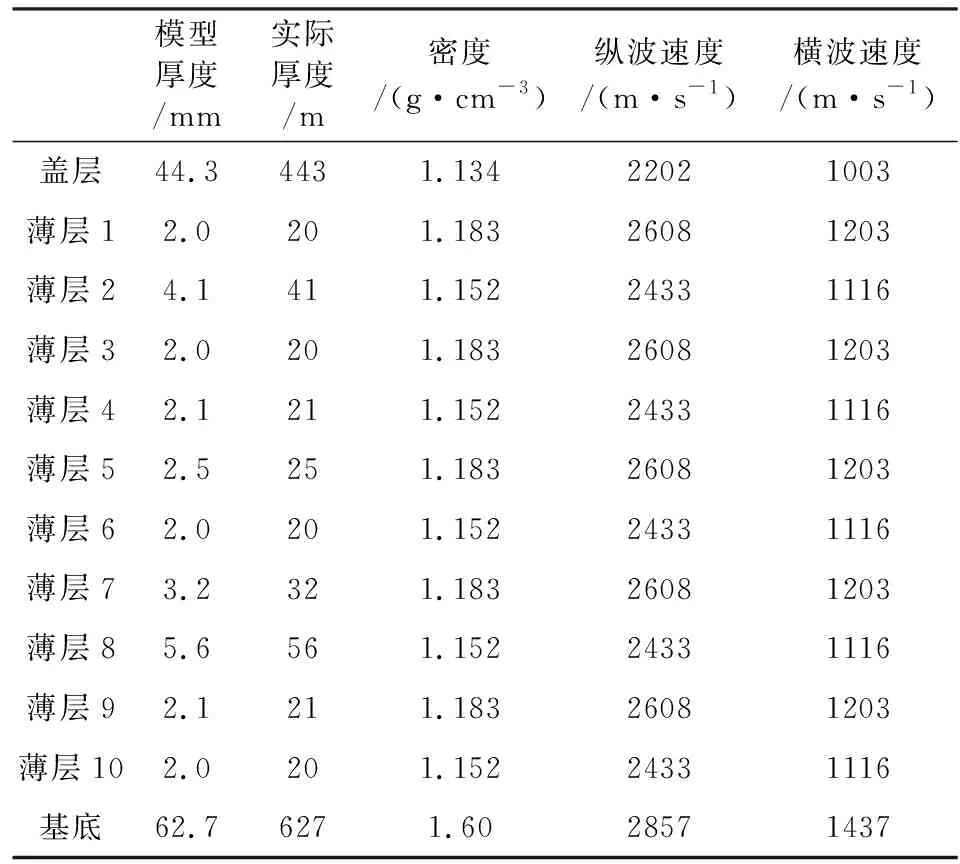
表2 物理模型各地层参数Table 2 Parameters for all layers of the physical model

2 数据采集及处理

2.1 数据采集及转换

受实验设备和实验场地的限制，在实验室条件下无法直接获得与野外地震频带接近的模拟地震数据(<100 Hz).因此，想要获得与野外地震频带接近的模拟结果，需要分两步进行：首先，在实验室条件下按照一定的比例尺制作物理模型，并按照物理模型实际尺寸模拟超声频带的地震记录(>20 kHz)；然后按照相似性原理，将实验室物理模型上超声频带地震数据(>20 kHz)转换成野外地质模型上接近实际野外地震频带的模拟地震数据(<100 Hz).这种转换需要设置一定的相似比，如前文所述，本研究中尺寸相似比设定为1∶ 10000(物理模型实际尺寸与对应野外地质模型尺寸之比)；速度相似比设定为1∶ 1(地震波在物理模型中的传播速度与在野外地质模型中传播速度之比).除此以外，还需要设定频率相似比和采样率相似比，频率相似比定义为实验室环境下激发的地震波频率与对应的野外地震波频率之比，在本研究中设定为10000∶ 1；采样率相似比定义为实验室环境下采集地震波的采样率与野外采集地震波的采样率之比，在本研究中设定为1∶ 10000.表3中给出了实验室采集参数与对应的野外采集参数，以及相似比.需要说明的是，在实验室采集过程中需要将模型置于水中，并使激发换能器和接收换能器都紧贴水面，这样做优点是可以较好的解决换能器与模型的耦合问题，使采集的地震数据的信噪比较高.实验室实际水深105 mm，按照本研究选定的尺寸相似比(1∶ 10000)，对应的地质模型上水深为1050 m(表3).

表3 实验室采集参数及野外采集参数Table 3 The laboratory acquisition parameters and field acquisition parameters

因此，本研究中物理模拟地震数据的采集可以表述为这样一个过程；首先在实验室条件下针对长度800 mm、宽度600 mm、水深105 mm、地层厚度为134.6 mm的实验室物理模型，采集一套震源主频为300 kHz、采样率0.1 μs的地震数据；随后，将该地震数据转换为在一个野外地质模型上采集的震源主频30 Hz、采样率1 ms的地震数据，该野外地质模型长度为8000 m、宽度为6000 m、水深1050 m、地层总厚度为1346 m，并且该野外地质模型中的水层以及各地层的速度和密度与实验室物理模型中的速度和密度(表1、表2)保持一致.转换的依据是相似比，转换的过程由物理模拟系统自动完成，本论文中后续所有的数据分析，均是基于转换后的地震数据，即在野外地质模型上采集的震源主频30 Hz、采样率1 ms的地震数据.

在本研究中共采集了4条测线，测线的分布如图3a、图4a中红线所示，其中测线1和测线2沿X方向，测线3和测线4沿Y方向.首先沿着各条测线进行了一次覆盖采集，其采集方式如图5a所示.在一次覆盖采集的过程中，单炮激发，单道接收，炮检距(激发换能器与接受换能器的间距)为200 m (对应实验室物理模型上的距离20 mm)，且固定不变，每次炮点前进10 m (对应实验室物理模型上的距离1 mm)，共采集781道数据.随后，对4条测线进行多次覆盖采集，4条测线的多次覆盖采集参数相同，如表3所示.由于模型的长度和宽度尺寸不同，测线1、2和测线3、4的长度略有差异，导致其炮数不同，测线1、2共有356炮，测线3、4有254炮.

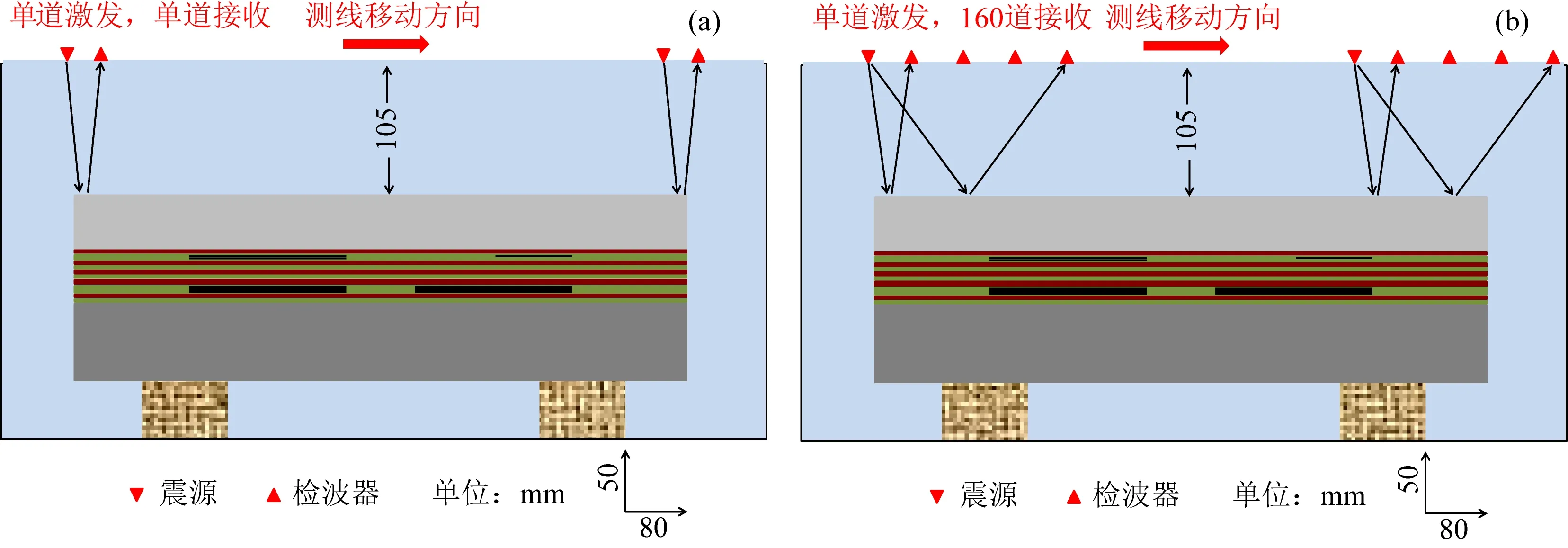
图5 采集方式意图(a) 一次覆盖; (b) 多次覆盖.Fig.5 Schematic diagram ofacquisition geometry(a) Single coverage; (b) Multiple coverage.

2.2 原始数据分析及数据处理

一次覆盖采集所得的剖面与自激自收剖面类似，但由于激发换能器和接收换能器的间距，激发点和接收点并不完全重合，存在着一定的偏移距，因此并不是严格的自激自收剖面.最终所得的一次覆盖剖面如图6所示，从图中可以看出模型底界面的反射波走时约为2.6 s，全程多次波走时晚于模型底界面反射波，这说明采集参数和水层深度选择恰当，可以避免全程多次波的影响；此外，从一次剖面中可以很清晰的识别出水层以及模型的各个部分，其结果被标注在图6中.

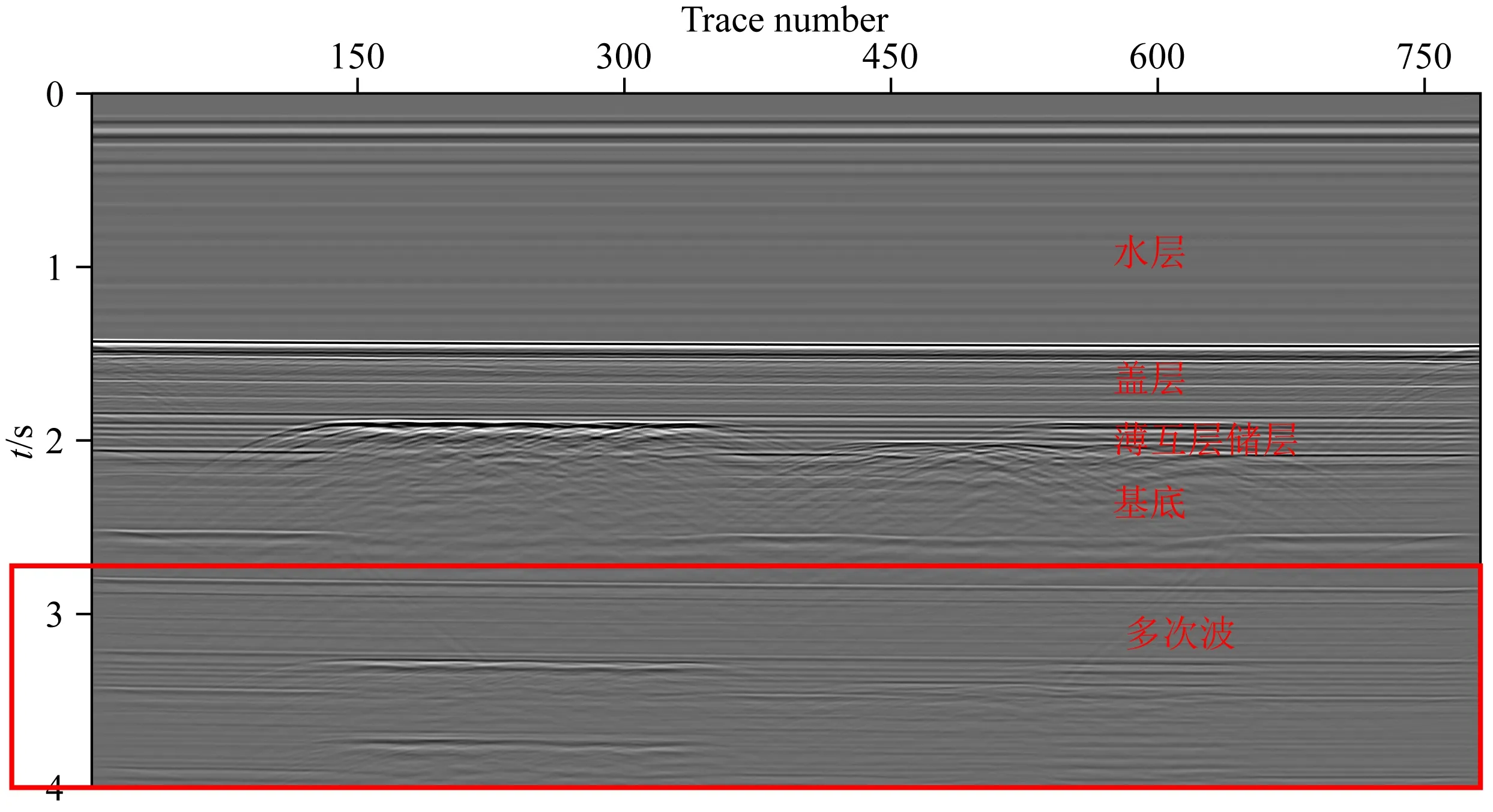
图6 测线1一次覆盖剖面Fig.6 Single coverage section for line 1

多次覆盖采集所得单炮记录如图7所示，各个界面的反射波及多次波被标注在图中.由于物理模拟所采集的模拟地震资料信噪比相对较高，在切除直达波并进行简单的滤波处理以后，可以直接进行速度分析，然后进行叠加偏移处理.本研究以测线1为例，分别测试了有限差分法叠后时间偏移(由开源软件Seismic Unix提供)和克希霍夫积分法叠前时间偏移处理(由商业软件CXTOOL提供)流程，获得了叠加剖面、叠后偏移剖面以及叠前偏移剖面，测线1的测试结果如图8所示.

图7 单炮记录Fig.7 Record of single shot

图8a显示是测线1的叠加剖面，从图中已经可以清晰的识别出模型顶、底界面以及薄互层部分.叠加剖面上红色箭头标注的是由裂缝边缘产生的绕射波，尽管在制作裂缝单元过程中，已经尽可能使其边缘光滑，但是由于裂缝单元的边界与周围岩层存在弹性性质的差异，从而不可避免的产生绕射波并对识别裂缝单元造成干扰.此外，绿色箭头指示的是模型的边界效应，实际地层在水平方向可以看作是无限延伸的，但是在制作物理模型的过程中必须进行截断，因此会产生人工边界，导致边界反射.对于底部边界产生的边界反射，可以适当控制模型的厚度以及采样时长，避免这些边界反射干扰有效信号；但来自侧面的边界反射则很难避免.图8b为叠后偏移的结果，对比图8a和图8b可以发现，裂缝单元边缘位置的绕射波干扰问题得到了一定程度的改善，但是截断边界的反射波仍然不能收敛，边界反射的问题仍然存在.图8c为叠前时间偏移的结果，边界反射及绕射波的问题都得到了较好的解决，为后续地震响应特征分析提供了良好的基础.

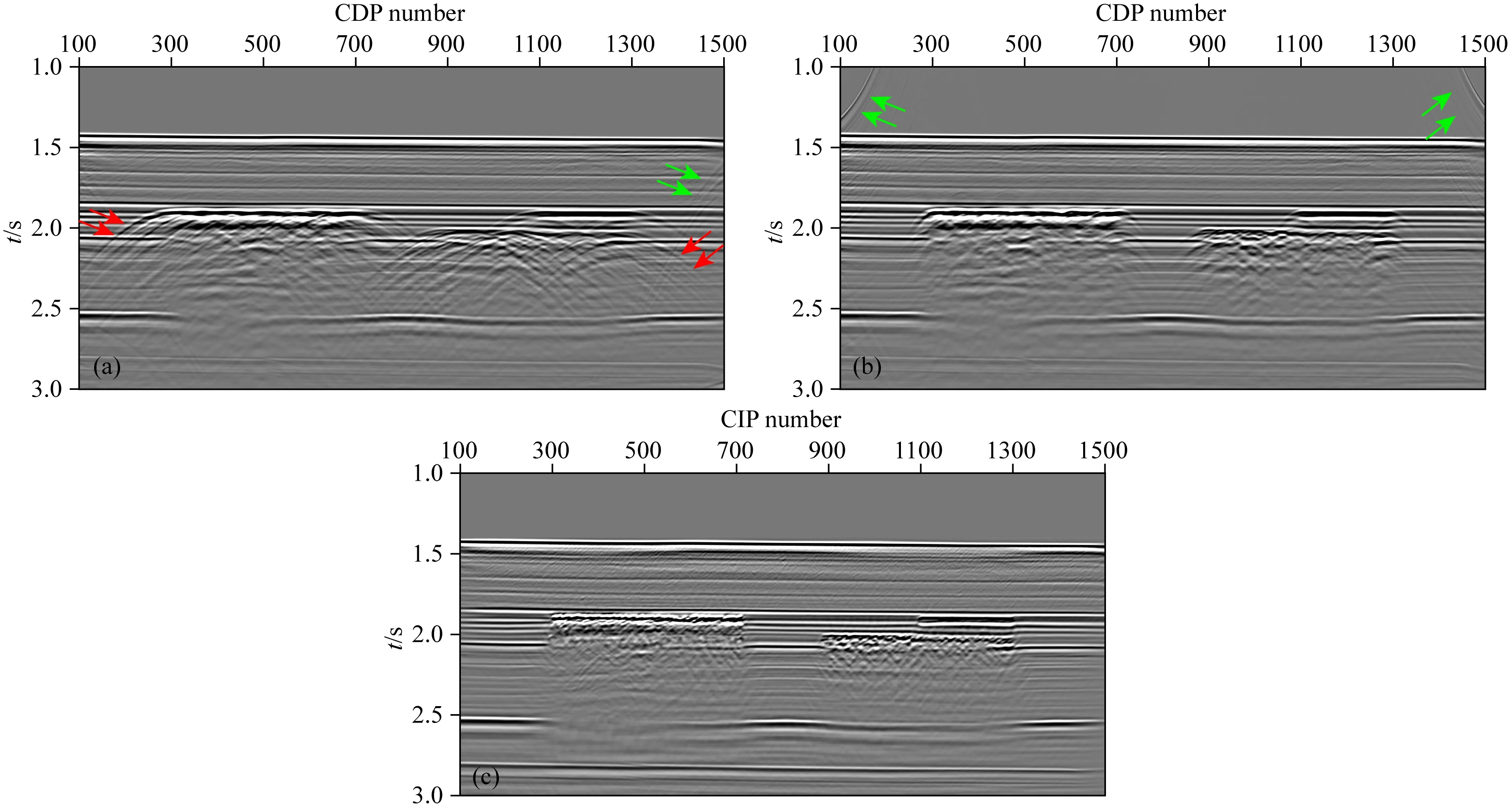
图8 测线1数据处理结果(a) 叠加剖面; (b) 叠后偏移剖面; (c) 叠前偏移剖面.Fig.8 Processed data for line 1(a) Stacked profile; (b) Post-stack migration profile; (c) Pre-stack migration profile.

此外，无论一次覆盖还是多次覆盖的结果，在模型顶界面反射与薄互层反射之间，存在着一些微弱的反射界面(图6、图8).在本研究中为了尽可能的降低模型顶底界面的边界反射，盖层和基底的厚度都设计的比较大；为了保证大厚度的盖层和基底在胶结过程中不发生变形，保证胶结固化的质量，盖层和基底均是分4次胶结而成.无论是对盖层还是对基底而言，尽管所用材料相同，每一次胶结的接触部位仍会产生一个微弱的反射界面，即“浇筑痕迹”.盖层中的浇筑痕迹较为明显，基底中的浇筑痕迹因为受到多次波和绕射波的影响，并不明显.从地震剖面上看，浇筑痕迹的反射波能量比目的层反射波能量弱得多，因此，浇筑痕迹的存在对后续响应特征分析的影响不大，可以忽略.

3 地震响应特征分析

3.1 处理结果分析

目的层的处理结果如图9所示，通过有“水平缝”的位置和无“水平缝”的位置的地震记录进行对比，可以明确“水平缝”产生的地震波异常.总的来说，有裂缝的位置产生明显的振幅异常增强、极性反转、同相轴错断等现象，裂缝特征清晰明显，这也说明本研究模拟方法的有效性.这种地震波异常实际上是由嵌入地层中的“水平裂缝单元”产生的.在制作这些裂缝单元的过程中，考虑了水平裂缝产生的层理结构以及裂缝的内部空间，每个裂缝单元包含多条裂缝，其在构成上更接近“一组定向排列的裂缝”或者“裂缝带”.不同裂缝单元之间以及同一个裂缝单元的不同位置之间，地震响应特征会出现差异，反应了裂缝物性特征的变化.裂缝介质是用片状材料叠合法来模拟的，在制作的过程中将粘合剂涂抹到片状材料上，然后将片状材料贴合在一起，经过机械压实后晾干固结.对比图9—图12可以发现，薄片的张数越多，裂缝介质的反射特征在剖面上就越明显.另一个影响裂缝性质的重要因素是裂缝单元的压实程度.在裂缝制作过程中，粘合剂可能会进入片状材料的孔隙空间中，当所有的片状材料孔隙均被粘合剂充填时，模拟的裂缝接近干裂缝；但是压实程度不够或者不均匀时，胶结物无法进入片状材料中的孔隙空间，导致片状材料孔隙中充填物较少，空气被封存在孔隙中，此时裂缝更接近含气裂缝.

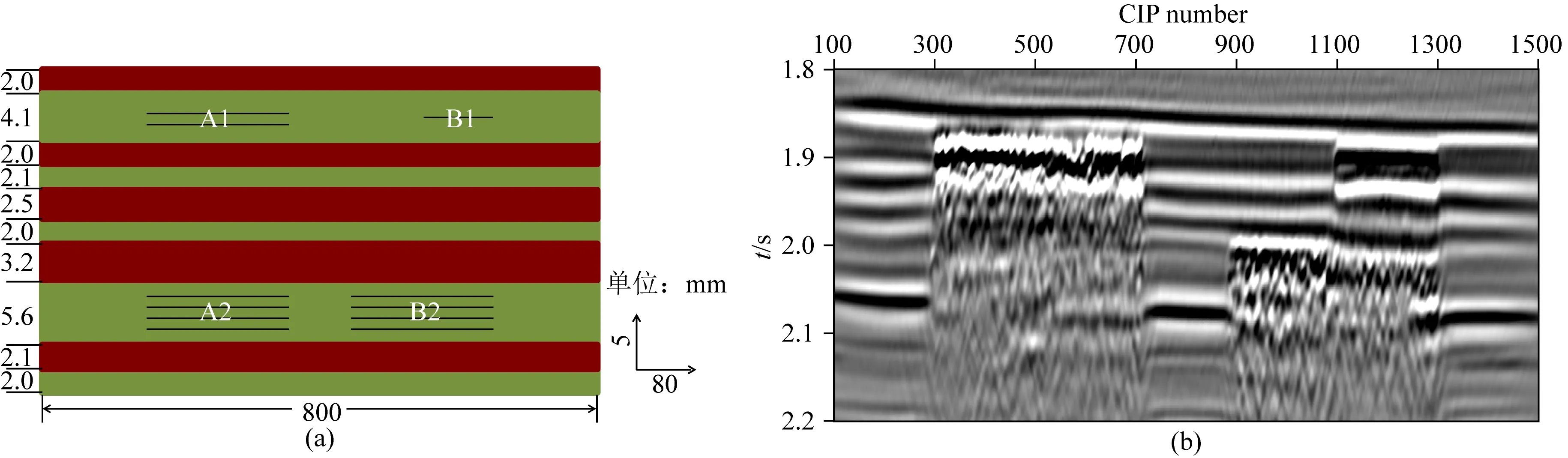
图9 (a) 测线1薄互层垂向结构示意图; (b) 相应叠前偏移结果Fig.9 (a) Sketch showing vertical structure of the thin inter-bed layers for line 1; (b) Corresponding pre-stack migration result

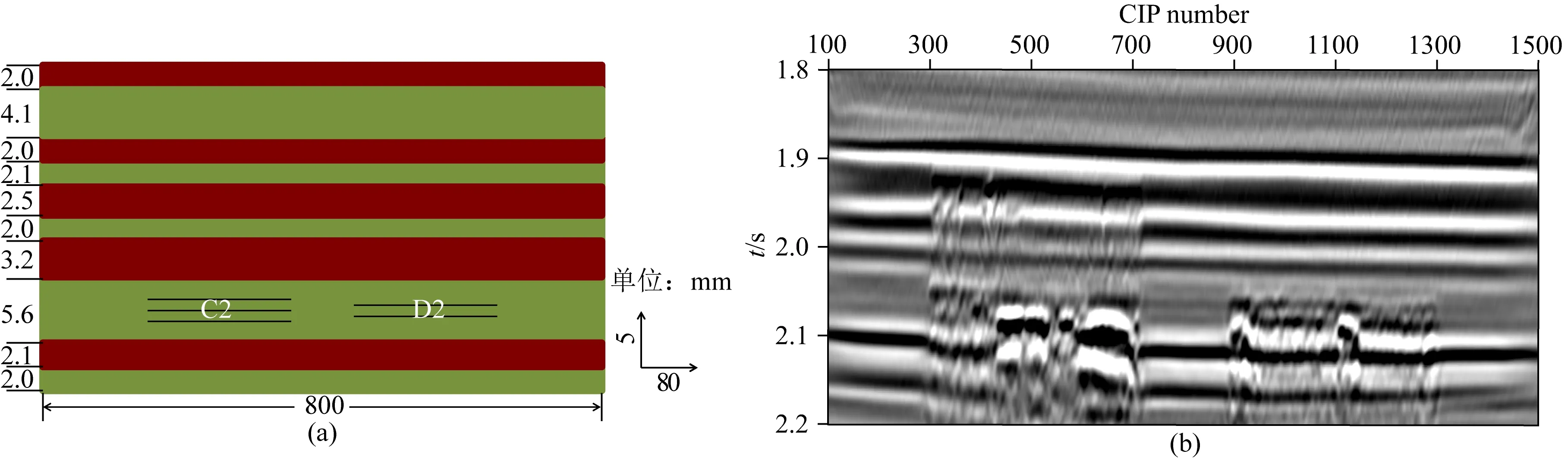
图10 (a) 测线2薄互层垂向结构示意图; (b) 相应叠前偏移结果Fig.10 (a) Sketch showing vertical structure of thin inter-bed layers for line 2; (b) Corresponding pre-stack migration result

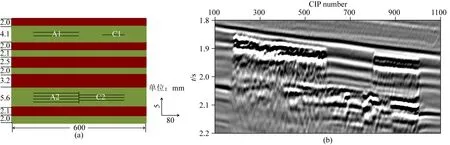
图11 (a) 测线3薄互层垂向结构示意图; (b) 相应叠前偏移结果Fig.11 (a) Sketch showing vertical structure of thin inter-bed layers for line 3; (b) Corresponding pre-stack migration result

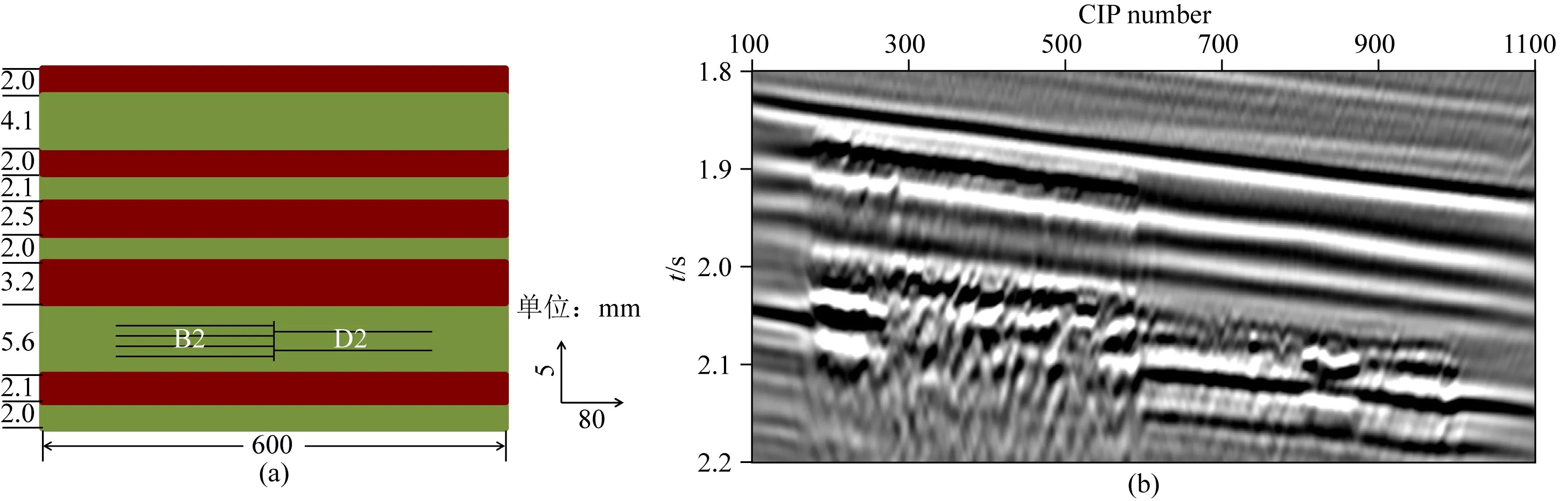
图12 (a) 测线4薄互层垂向结构示意图; (b) 相应叠前偏移结果Fig.12 (a) Sketch showing vertical structure of thin inter-bed layers for line 4; (b) Corresponding pre-stack migration result

3.2 含水平缝薄互层储层频率特征分析

本研究还以测线1为例，对模拟数据的时频特征进行分析.通过图9可以看出，裂缝单元A1的性质更接近于含气裂缝，且产生了一种屏蔽效应，纵波的传播能量严重衰减，导致裂缝单元A1下部的成像效果较差.相比之下性质更加接近干裂缝的B1裂缝单元，对下部裂缝单元B2的影响就没有A1那样严重.对测线1偏移数据的频谱分析结果表明，目的层能量都集中在0～60 Hz范围以内(图13).本研究选用了基于时频重排算法的光滑伪Wigner-Ville分布(RSPWVD)对地震信号进行时频分解，这种方法分辨率较高但计算效率比较低，考虑到本研究中数据量不是很大，选用该方法较为可行.提取5～55 Hz范围内的分频结果，用以分析地震响应的频率特征.由于不同频率之间本身存在能量的差异，本研究以模型顶界面作为参考平面，对不同频率成分之间的能量进行均衡.选择这个界面作为参考主要是因为模型顶界面是水和弹性盖层的交界面，可以认为是弹性界面，其反射系数与入射波的频率成分无关，入射波经过顶界面反射以后，各频率成分能量的相对强弱不发生改变.

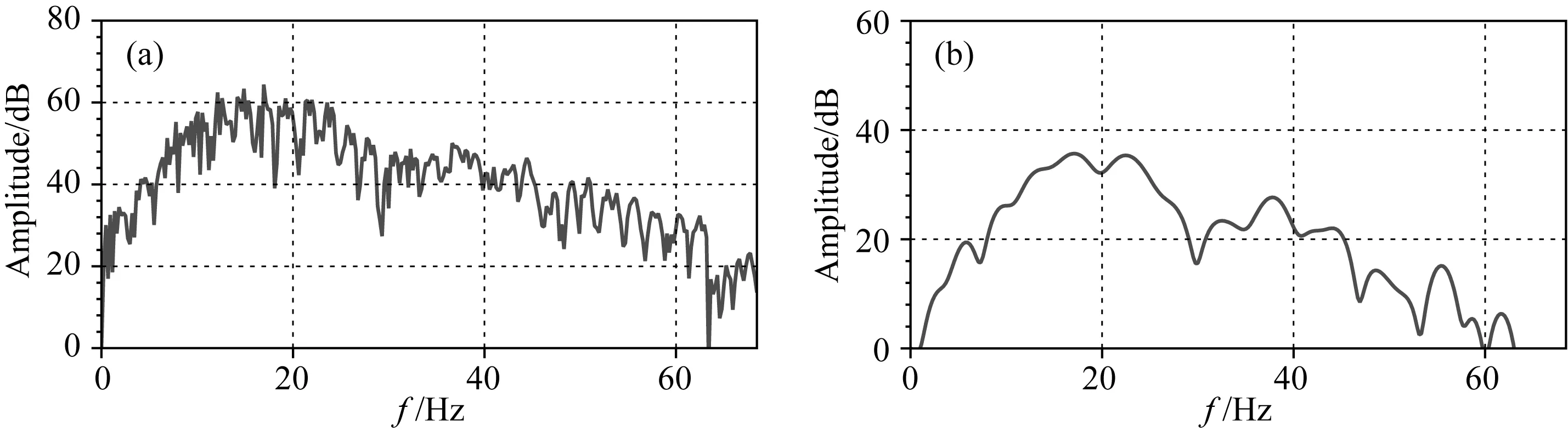
图13 测线1频谱分析(a) 时窗为1.2～2.6 s, 包含物理模型顶底界面反射及薄互层反射; (b) 时窗为1.8～2.2 s, 仅包含薄互层反射.Fig.13 Amplitude spectrum of surveyr line 1(a)Time window is 1.2～2.6 s, which contains reflections of top interface and bottom interfaces as well as thin inter-bed layers; (b) Time window is 1.8～2.2 s, which contains only reflections of thin inter-bed layers.

图14中显示的是第200、400、600、800、1000、1200个CIP(共成像点，Common Image Point)的单道时频谱分解结果.第200个CIP处是不发育水平裂缝的薄互层，在该位置上地震响应特征完全由薄互层决定；其时频谱上对应有两个峰值，一个出现在浅层低频段，另一个出现在深层高频段，且浅层的能量较强.第400个CIP的分解结果指示的是裂缝单元A1和A2响应特征，从图中可以看出，在浅层出现了一个强能量带，贯穿整个频带始终，深层几乎没有信号，只有在低频段有一个能量较弱的峰值，该位置裂缝中含气量较高，因此在浅层出现强能量带，且由于高阻抗的屏蔽作用使得深部能量很弱.通过时频特征来看，含气较高的是裂缝单元A1，由于A1的存在严重的影响了A2单元的识别，A2单元的响应被严重削弱，仅仅在低频段存在一个微弱的峰值.第1000、1200个CIP反应的是裂缝单元B1、B2的响应，从图中可以看出这两个CIP的响应特征较为复杂，峰值较多，且分布无规律，这是薄互层调谐效应与裂缝介质综合作用的结果.

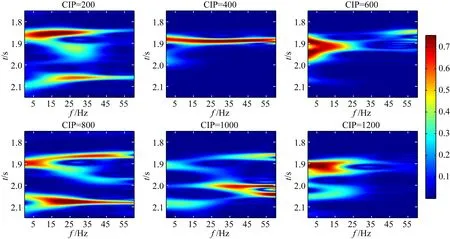
图14 不同CIP单道时频分析结果(频率范围5～55 Hz, 时间范围1.8～2.2 s)Fig.14 Spectrum decomposition results of single CIP from 5 Hz to 55 Hz with the time window 1.8 s to 2.2 s

将偏移剖面划分三部分：第一部分为CIP 160～280，主要刻画不发育裂缝的薄互层的地震响应特征；第二部分为CIP 280～720，主要针对裂缝单元A1和A2的响应特征；第三部分为CIP 880～1320，主要描述了裂缝单元B1和B2的响应特征.然后将这三部分剖面进行时频分解，获得分频剖面，其结果如图15所示.图15a中展示的是CIP 160～280的分频结果，从模型的薄层结构可以看出，由于要在第2薄层和第8薄层内嵌入裂缝介质因此厚度较厚，而第一薄层与第9、10薄层以及中间的第3～7薄层都较薄，这导致两个较厚的薄层将整套薄互层的响应特征明显地划分成三个能量团：第一个能量峰值对应的是薄层1的顶底界面的叠加，第三个峰值对应的是第9薄层的顶界面、底界面以及第10薄层底界面的反射波叠加，中间的能量则对应的是第3～7薄层所有顶底界面的反射.随着频率的升高，薄层部分的同相轴数量增多，且能量相对增强.此外，还可以看出，对25 Hz以后的频率成分，其能量出现了明显的横向不均匀性，这一现象产生的原因是随着CIP位置不断靠近裂缝单元A1和A2，裂缝单元对地震波传播的影响逐渐增强.

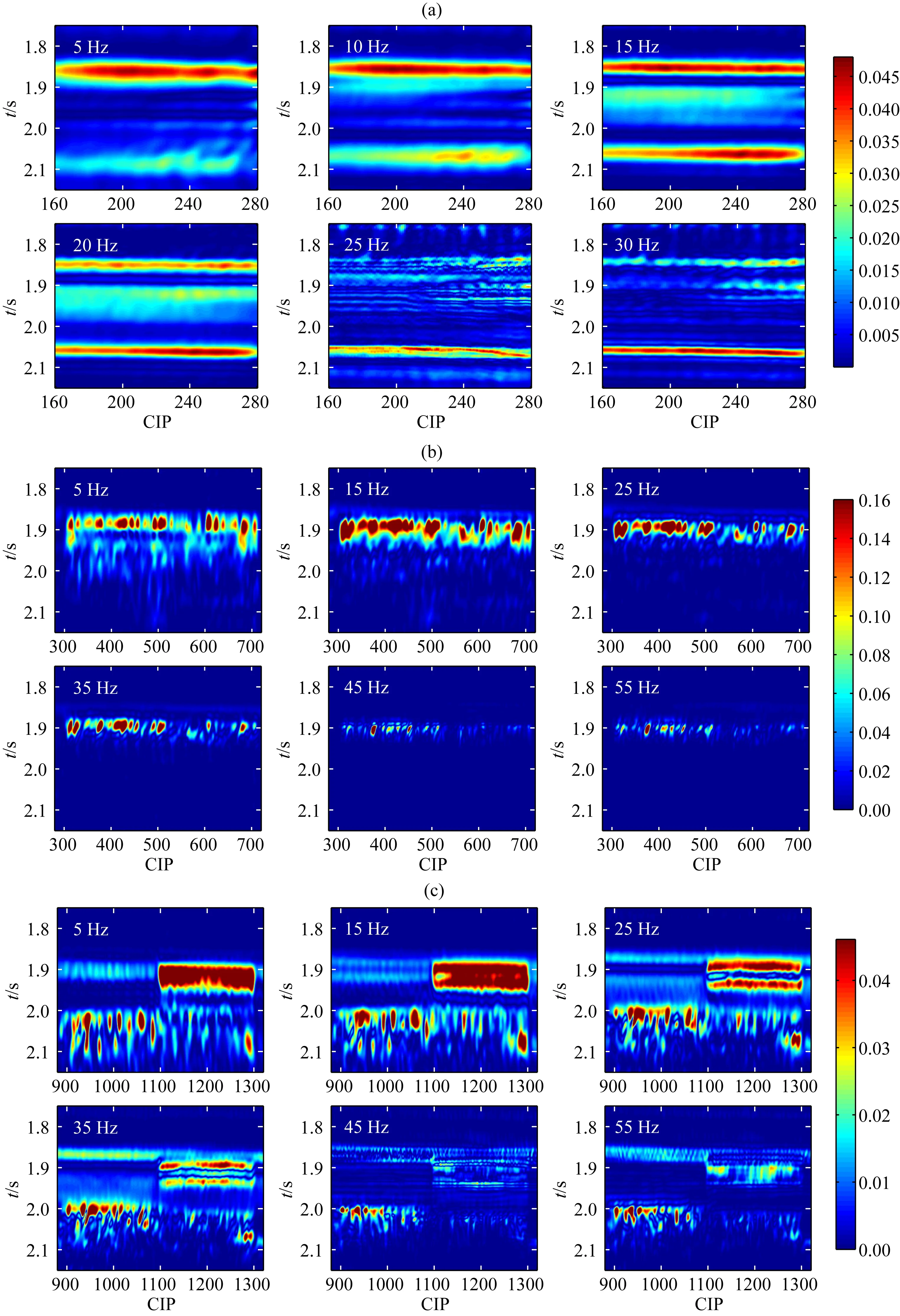
图15 不同频率的分频剖面(a) CIP 160～280; (b) CIP 280～720; (c) CIP 880～1320.Fig.15 Spectral sections for different frequencies

图15b为CIP 280～720的分频结果.从图中可以明显看出，裂缝单元A1的低频能量较强，表现出低频亮点的特征.由于A1的存在，A2的响应难以识别，只有在5 Hz的剖面上隐约的识别出A1和A2的界限，这也与单道时频分析的结果相一致(图14).图15c为CIP 880～1320分频结果.类似的，裂缝单元B1表现出明显的低频亮点.但是，裂缝单元B2并没有引起明显的亮点特征.与裂缝单元A1和A2相比，裂缝单元B1和B2的响应始终都是分离的，即便从偏移剖面上也可以很明显地区分两个单元.B1的横向展布宽度为B2的一半，这样的设计便于分析在不同频段内上部裂缝单元对下部裂缝单元的影响.在低频时，B1对B2的影响并不大，B2响应特征并没有表现出明显的横向差异；在高频段，B2对B1的影响明显增强，在55 Hz时B2的响应几乎消失，B1裂缝对中间薄互层响应的影响类似.以上的分析结果表明，水平裂缝的存在，会使地震信号的频率特征产生明显的异常.这就意味着，可以用频变属性进行水平裂缝的识别，但需要注意的是，薄互层的调谐效应也可以使地震信号产生频变特征，这在一定程度上干扰了水平缝的识别.

图16所示为测线1上几处CDP(共深度点，Common Depth Point)的频变AVO曲线.图16a为模型顶界面的频变AVO曲线，如上文所述，模型顶界面可以视为纯弹性界面，因此其AVO并没有频变特征，各频率成分之间的AVO曲线基本重合.图16b为CDP 200处薄互层频变AVO曲线，在该位置处没有水平裂缝，其频变AVO特征完全是由调谐效应产生的.从图中可以看出，低频和高频段的频变AVO特征有明显的区别，在低频段振幅随着偏移距的增大而减小，在高频段振幅随着偏移距先增大达到某一峰值后再减小.并且对比图16b、c、d可以发现，无论有无裂缝、以及裂缝参数如何，其频变AVO特征的基本模式没有发生改变，这意味着薄互层调谐效应产生的影响起主导作用.但是，裂缝的引入导致了频变AVO特征可以发生明显改变，频变AVO曲线的变化趋势、高频峰值振幅对应的偏移距位置，以及不同频率成分之间的分散程度，都有较为显著的差异.这也就意味着如果可以通过地质、测井、岩心等资料，建立了较为准确的背景薄互层的地质模型，然后利用频变AVO属性进行横向对比，可以用于水平裂缝横向分布的识别.

图16 频变AVO曲线(a) CDP 200处, 模型顶界面频变AVO曲线; (b) CDP 200处, 薄互层储层部分频变AVO曲线; (c) CDP 400处, 薄互层储层部分频变AVO曲线; (d) CDP1000处, 薄互层储层部分频变AVO曲线.Fig.16 Curves of frequency dependent AVO(a) Top at CDP 200; (b) Thin inter-bed reservoir at CDP 200; (c) Thin inter-bed reservoir at CDP 400; (d) Thin inter-bed reservoir at CDP 1000.

4 结论

本研究通过片状孔隙材料定向粘合的方式模拟裂缝介质，进而模拟了含水平裂缝薄互层储层的地震响应特征.数据分析结果表明，本研究的模拟方法有效，所得的水平裂缝地震响应特征清晰、明显.从二维地震响应的时频分析结果来看，薄互层中的水平裂缝可以明显的引起时频谱异常，但是能否会出现低频亮点，却要视情况而定.上层裂缝对下层裂缝的影响，在不同频段内存在差异.因此可以在低频段区分耦合的两组裂缝响应.总的来说，薄互层中水平裂缝的响应特征，受到薄互层调谐效应和裂缝介质的双重影响，在进行薄层解释及裂缝预测时必须综合考虑.最后，本研究还验证了频变AVO方法对于含水平缝薄互层储层识别的适用性，对于频变AVO响应特征而言，薄互层产生的频变特征起主导作用，但是裂缝发育以及裂缝参数的变化可引起频变AVO特征的显著变化，在预先建立薄互层背景模型的前提下，可以通过频变AVO属性识别水平裂缝的横向分布.