闭环光纤电流传感器高阶动态模型及仿真

李 奇，李传生，赵叶铭，邵海明，蔡晋辉

(1.中国计量大学，浙江 杭州 310018；2.中国计量科学研究院，北京 100029；3.北京信息科技大学，北京 100192)

1 引 言

脉冲功率技术以高电压、大电流、强功率为主要特征，在电磁发射、电磁弹射、大功率激光、电磁脉冲、核物理、生物医疗、环境工程等领域应用广泛[1,2]，脉冲大电流测量技术是脉冲功率研究中的关键技术[3,4]。

目前，罗氏线圈是被普遍采用的脉冲大电流传感器。该传感器的主要问题是：测量精度易受母线偏心及外部杂散磁场的影响[5]；超大电流全量程校准实现困难，只能接受“低校高用”。基于Faraday磁光效应的光纤电流传感器具有测量精度高、频响范围宽、动态范围大、绝缘性好、抗杂散磁场干扰能力强等特点，采用多圈敏感环倍增Faraday效应可实现全量程线性度的等效校准，保证量值的溯源性[6～8]。光纤电流传感器在高压大电流测量领域具有广阔的应用前景。

脉冲电流测量对光纤传感器的宽频测量能力提出了较高的要求，作为研究基础，需要建立光纤电流传感器高阶动态模型，对其时域及频域特性进行深入研究和优化。目前已有研究认为光纤电流传感器可近似为一阶系统，并建立了一阶动态模型进行仿真研究[9～11]，但是，该模型不能很好地反应传感器的高频特性。实际上，光电探测器、前置放大器及调制器驱动电路呈现低通特性，反馈通道存在延时，这些因素使得传感器成为高阶系统，动态模型、时域及频域特性均需要展开进一步研究。针对上述问题，本文推导并建立了光纤电流传感器高阶动态模型，基于Simulink对传感器的频响特性及阶跃响应特性进行仿真分析，经实验验证，仿真结果与实验结果一致，证明了模型的准确性。该模型为闭环光纤电流传感器宽带电流测量能力的评估提供依据。

2 工作原理

光纤电流传感器主要基于Faraday磁光效应及安培环路定律。如图1所示，光源发出的光经过三端口环行器由偏振器转为线偏振光，经45°光纤熔接点被均分，并沿保偏光纤的快轴和慢轴传输。1/4波片将线偏振光分别变为左旋、右旋圆偏振光。两束圆偏振光沿传感光纤传输，在被测电流的作用下，两束圆偏振光之间产生相位差。经传感光纤末端反射镜反射，两束圆偏振光沿原路返回，相位差加倍。再次经过1/4波片，两束圆偏振光再次转换为线偏振光，但偏振模式发生了互换。两束线偏振光由45°方位的起偏器检偏，并发生干涉。最后，携带被测电流信息的干涉光强信号经光电探测器变为电压信号，经前置放大、A/D高速采样转换变为数字信号，进行闭环信号处理[12]。

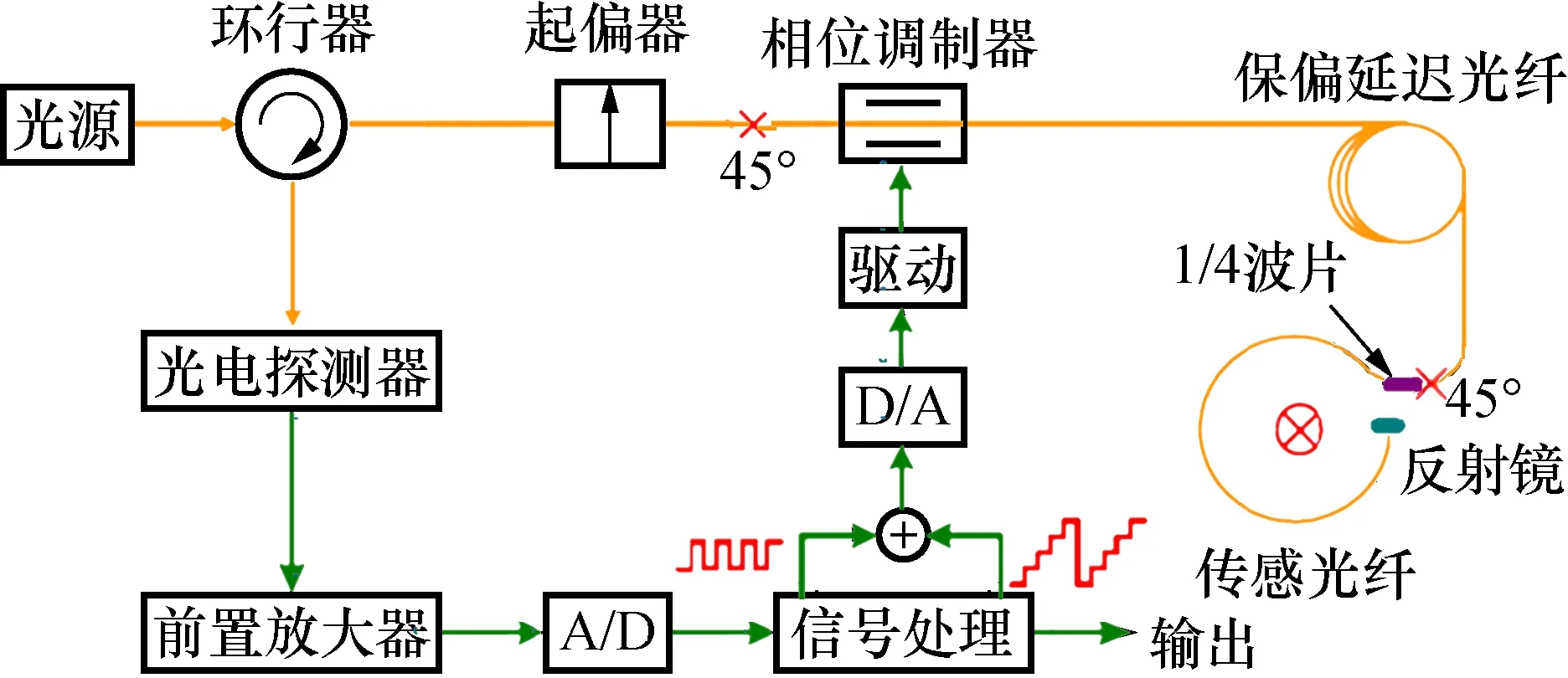
图1 光纤电流传感器原理示意图Fig.1 Configuration of fiber-optic current sensor

根据闭环控制算法，闭环检测系统在相位调制器上施加方波和阶梯波调制信号。方波调制信号交替引入± π /2调制相位，保证系统工作在最高灵敏度，阶梯波调制实时抵消Faraday相移，使系统锁定在 π /2工作点，避免余弦函数周期多值影响，提高传感器线性度及动态范围[13～16]，同时阶梯波的相位复位不会对测试结果产生影响[17]。

3 模型组成及推导

3.1 传感器高阶模型推导

根据闭环光纤电流传感器原理，可得到整个系统的动态模型，如图2所示，建模时着重考虑了光电转换、前置放大器、调制驱动电路等的高阶特性以及反馈延时。

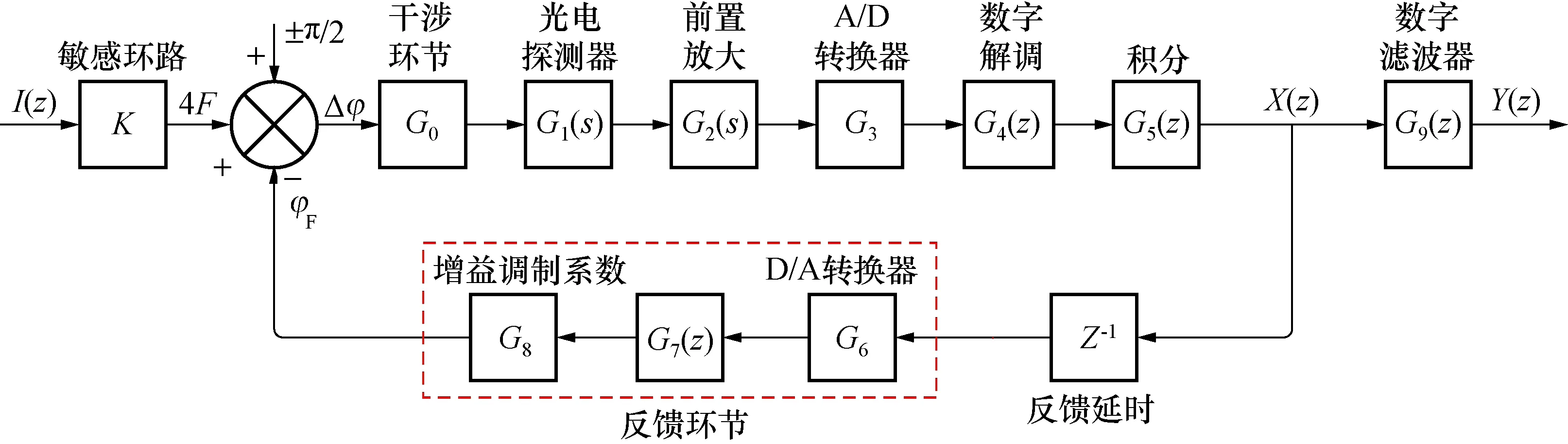
图2 光纤电流传感器动态模型Fig.2 Dynamic model offiber-optic current sensor

(1) 敏感环路，根据Faraday磁光效应，在敏感环路处由被测电流引起的Faraday相位差φs=4F=4VNI，其中，F为Faraday相移，V为传感光纤的Verdet常数(V=1.02 μrad/A@1.31 μm)，N为光纤圈数，I为被测电流。该环节可视为比例系数K=4VN的比例环节。

(2) 干涉环节，根据传感器闭环检测原理，引入方波调制及闭环反馈后，根据小偏差线性化原则，干涉光强可表示为[18]：

(1)

式中：φF为反馈相移。因此，干涉环节可视为比例环节，比例系数G0=αP0/2，式中α为光路损耗，P0为光源输出光功率。

(3) 光电探测器，光电探测器由光电二极管及跨阻放大器组成，将入射的光强信号转换为电压信号，其传递函数为：

(2)

式中：G1为光电探测器的电压响应度，V/W；B为光电探测器的带宽，Hz。

(4) 前置放大器，如图3所示，前置放大器对探测器输出的方波信号进行不失真放大。

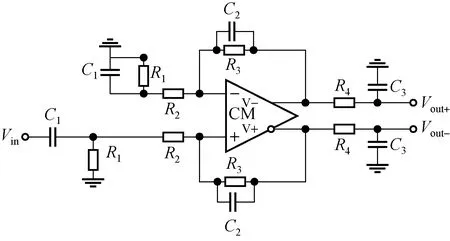
图3 前置放大电路Fig.3 preamplifier circuit diagram

传递函数可表示为：

(3)

式中：G2=R1R3C1/R2。

(5) A/D转换器，A/D转换器将前置放大器输出信号转为数字信号，忽略量化误差，可视为为比例环节，G3为A/D转换增益。

(6) 数字解调，被测电流的数字解调通过干涉光强相邻正负半周采样值累加平均并相减得到，由比例环节和延迟环节组成，可表示为：

G4(z)=G4·(1+z-1)

(4)

式中：G4为干涉方波光强信号半周期的采样点数。

(7) 积分环节，传感器采用积分控制算法，对数字解调结果进行累加积分，并对积分结果进行增益调整，积分结果作为传感器的输出及反馈，动态模型可表示为：

(5)

式中：Fg为增益调整系数。

(8) 反馈环节，反馈环节由D/A转换器、驱动电路及相位调制器组成。D/A转换器近似为比例环节和零阶保持器的级联，G6为转换增益；集成光学相位调制器的响应带宽远大于调制信号带宽，可近似为比例环节，增益为G8；调制器驱动电路通常为放大滤波器，其电路如图4所示。

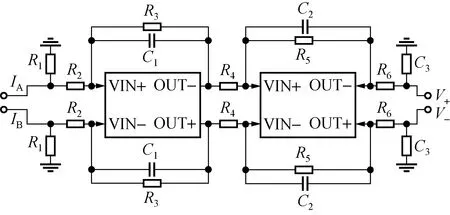
图4 相位调制器驱动电路Fig.4 Modulator drive circuit diagram

传递函数可表示为：

(6)

式中：G7=R1R2R5/(R1+R2)R4为调制驱动电路的增益；T1=R3C1、T2=R5C2、T3=R6C3分别为三级滤波器的时间常数。

将零阶保持器和相位调制器驱动电路传递函数进行离散化，得：

(7)

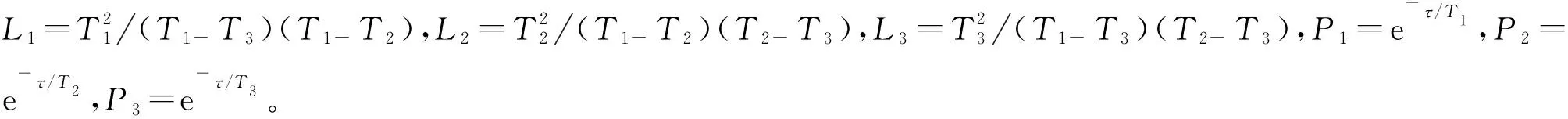
为避免阶梯波复位对传感器测量准确度的影响，D/A转换器数字信号的溢出产生2π复位，系统中D/A转换器的位数为15bit，故反馈增益恒为：G6G7G8=2π /215。

(9) 反馈延时，根据闭环信号检测原理，传感器的反馈控制周期等于渡越时间τ(信号光往返2次经过相位调制器的时间间隔为渡越时间)。反馈通道存在2个周期的延时：固有的反馈延时和A/D转换器输出延迟导致的反馈延时[19]。

(10) 数字滤波器，由于闭环信号检测系统的输出中含有大量噪声，因此选用M阶滑动滤波器进行滤波处理，根据滑动平均滤波器定义，可得输出序列：

(8)

其传递函数为：

(9)

3.2Simulink模型建立及仿真

3.2.1 Simulink模型建立

根据上述推导模型，建立基于Simulink的仿真模型，如图5所示。

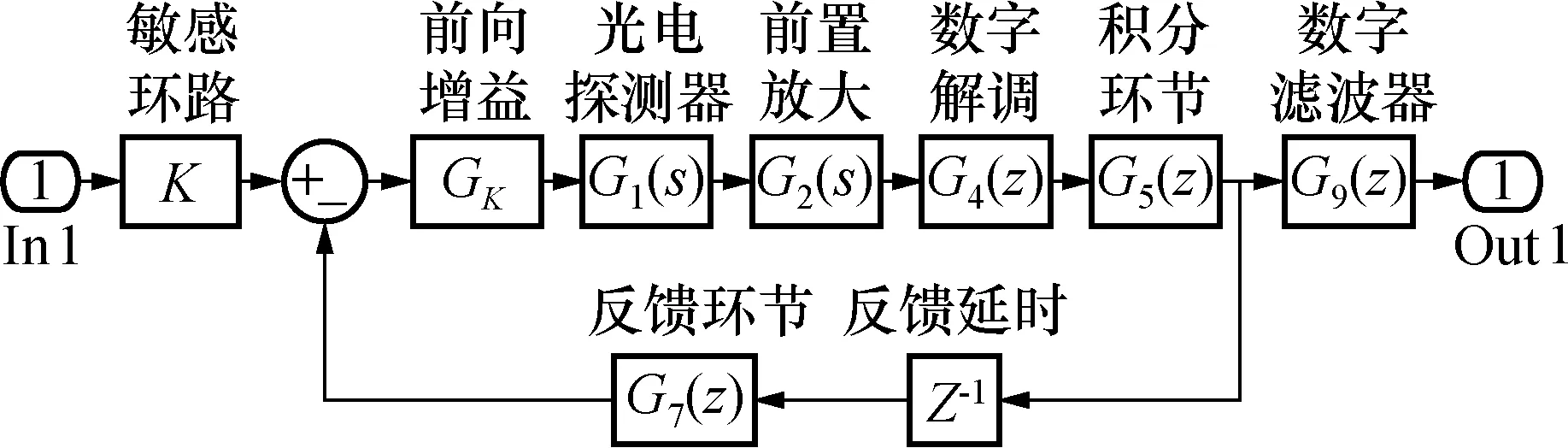
图5 Simulink仿真模型Fig.5 Simulink simulation model

其中：GF=G6G7G8/K为归一化系数，Gk=G0·G1·G2·G3·G4为前向增益，其具体测量方法为：传感器处于开环状态(仅施加方波调制信号)，由信号处理单元产生台阶高度固定为Ht的数字阶梯波，转换为模拟信号后施加在相位调制器上，则数字解调环节的输出为：

(10)

设置数字台阶高度Ht=10，图6所示为实测数字解调结果。为抑制噪声的影响，对采集到的数据进行均值运算，最终得到数字解调值为99.694 6，根据式(10)，得到前向总增益为51 993。

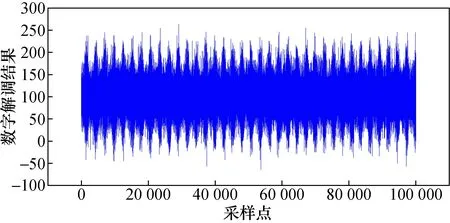
图6 实测数字解调结果Fig.6 Measured digital demodulation results

量化模型中各环节参数，结果如表1所示。

表1 各环节量化参数模型Tab.1 Quantitative parameter model of each link

3.2.2 阶跃响应特性仿真

根据闭环信号检测系统传递函数，将模型参数代入，可计算出系统的阶跃响应，仿真结果如图7所示，表2给出了不同参数下系统时域特性指标的计算结果。

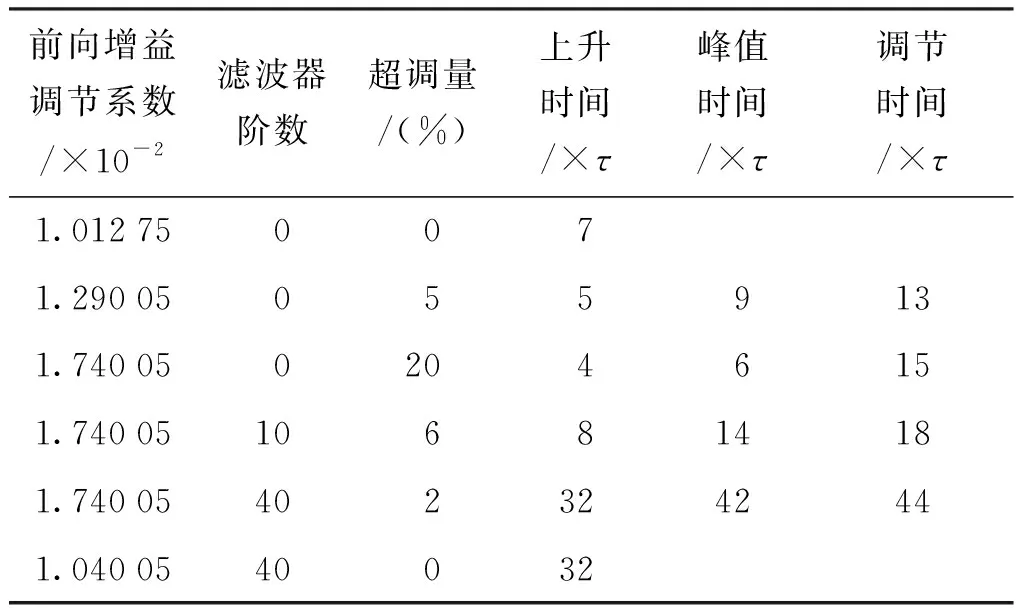
表2 光纤电流传感器阶跃响应指标计算结果Tab.2 Calculation result of step response index of Fiber-optic current sensor

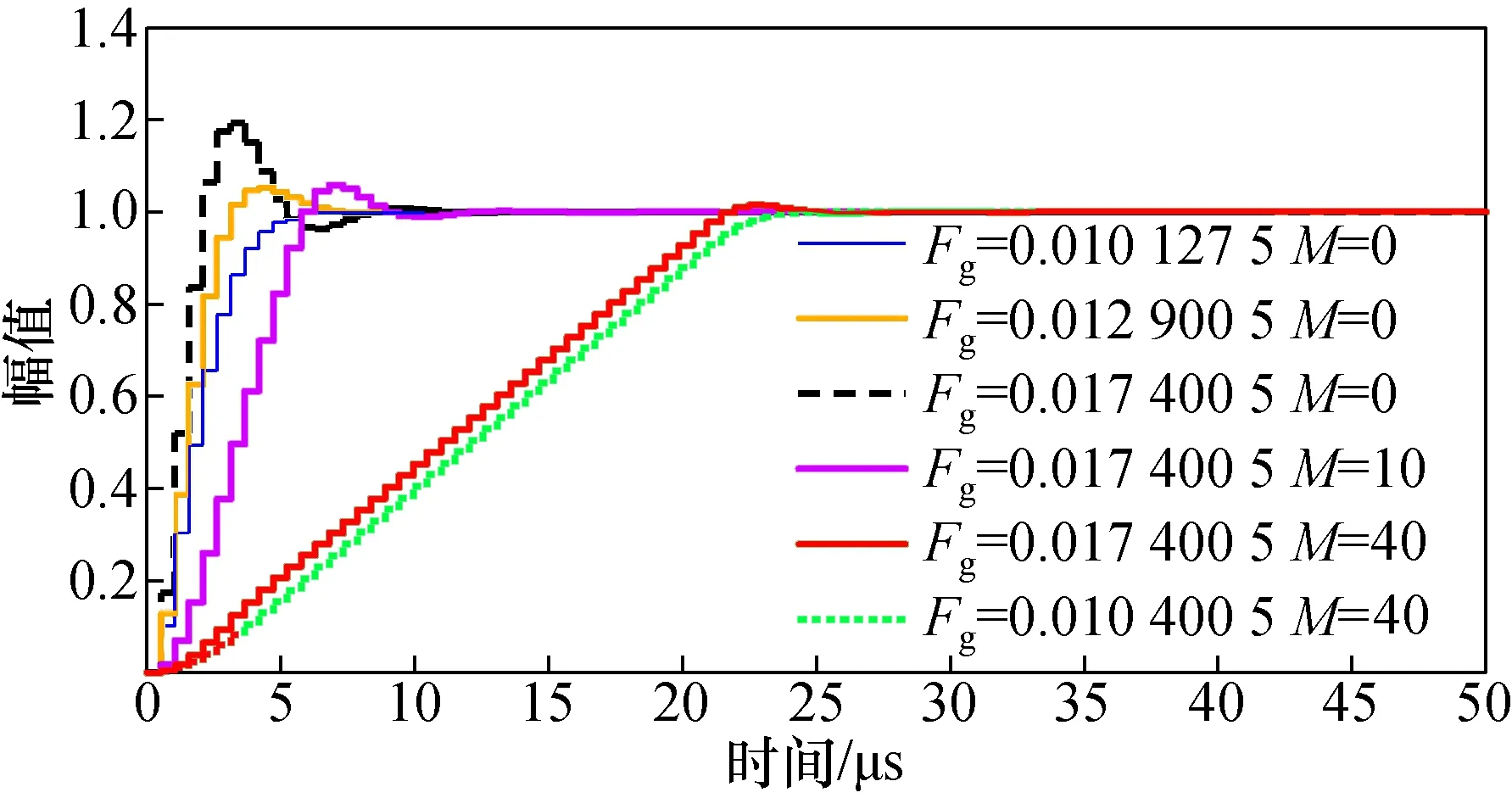
图7 阶跃响应仿真Fig.7 Step response simulation

由于反馈延时及光电探测器、前置放大器、调制器驱动电路的高阶特性影响，传感器闭环信号检测系统呈高阶特性。前向增益的大小直接影响系统响应速度，增大前向增益可提高响应速度，但前向增益过大将导致系统超调振荡。当前向增益调节系数Fg=1.012 75×10-2时，闭环检测系统无超调，上升时间为7个控制周期；当Fg=1.740 05×10-2时，闭环检测系统超调达20%，上升时间小于4个控制周期，峰值时间为7个控制周期，调节时间(响应降至1.5%的时间)为15个控制周期。

此外，输出滑动平均滤波器对超调振荡具有显著的抑制作用，但同时也会延长上升时间及调节时间。当Fg=1.740 05×10-2时，引入10阶滤波器，超调量由20%降至6%，上升时间延长至7个控制周期，随着滤波器阶数的增加，该效果愈加明显。当滑动滤波器阶数M=40时，超调量减小至2%，上升时间延长至32个控制周期，高阶数滤波器虽然可以抑制噪声，但也极大地降低了传感器的动态响应能力。

3.2.3 频率响应特性仿真

根据闭环信号检测系统传递函数，代入模型参数，可计算出响应的频率响应特性，结果如图8所示，表3给出了不同参数下系统频域特性指标的计算结果。

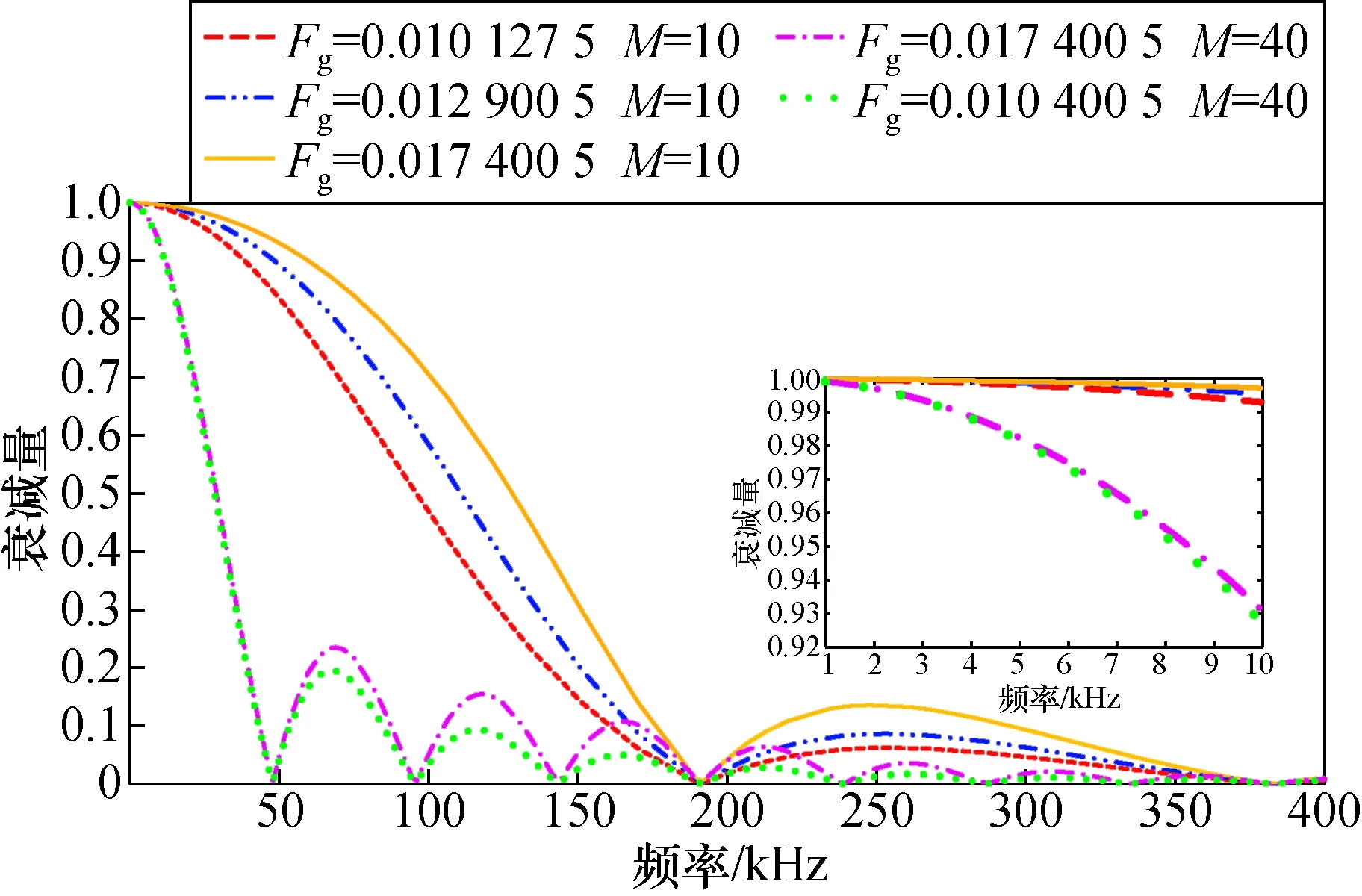
图8 频率响应仿真Fig.8 Frequency response simulation

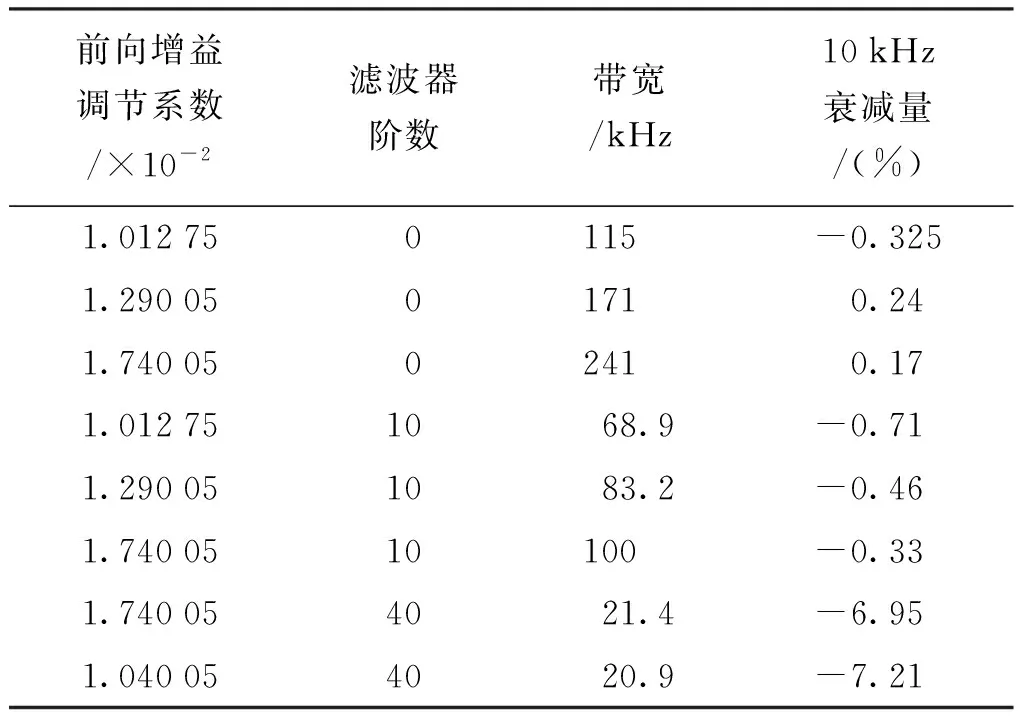
表3 光纤电流传感器频率响应指标计算结果Tab.3 Calculation result of frequency response index of Fiber-optic current sensor

前向增益的大小直接影响闭环系统的频率响应特性。设置滤波器阶数M=10，调节前向增益分别为Fg=1.012 75×10-2, 1.290 05×10-2,1.740 05×10-2，代入仿真模型，得到系统带宽分别为：68.9,83.2,100 kHz。因此，在满足系统闭环稳定的前提下，适当提高前向增益将有效改善系统的频率响应特性。

此外，滑动平均滤波器阶数直接影响系统带宽，当Fg=1.740 05×10-2，滑动平均滤波器阶数增加到40阶时，系统带宽降至21.4 kHz；当Fg=1.040 05×10-2，M=40时，系统处于临界状态，相较于未加滤波器的系统临界状态(即Fg=1.012 75×10-2，M=0)系统带宽减小81.8%，降至20.9 kHz。因此，在满足噪声抑制的前提下，降低滤波器阶数，减少对高频信号的衰减，将有助于提高系统带宽。

4 实验验证

4.1 阶跃响应测试

根据闭环光纤电流传感器检测原理，某一时刻在反馈阶梯波信号上同步叠加台阶高度为φΗ的阶梯波调制信号，使两束信号光之间引入非互易阶跃相位差，实现阶跃响应的等效测试。利用FPGA内部RAM IP核通过阈值触发高速记录阶跃响应数据，数据量达到设定长度时，传感器停止采样，并输出记录数据，相邻数据点的间隔等于渡越时间。图9给出了不同增益调节系数Fg下光纤电流传感器的阶跃响应测试结果，指标计算结果列于表4，测试结果与理论仿真基本一致，证明所建立模型准确。

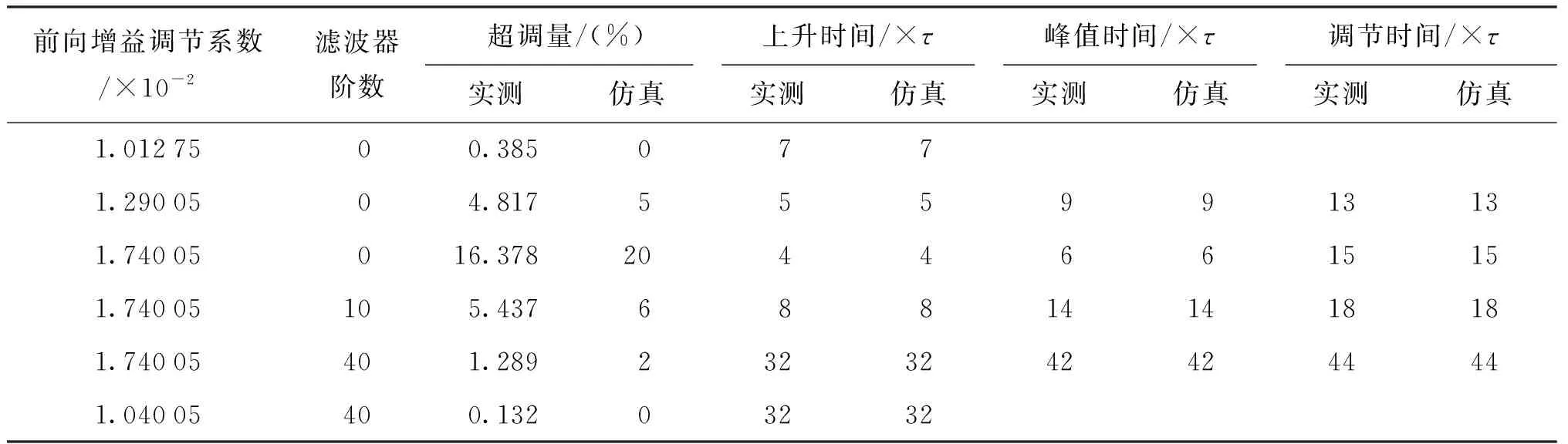
表4 光纤电流传感器实测阶跃响应指标Tab.4 Measured step response index of fiber optic current sensor

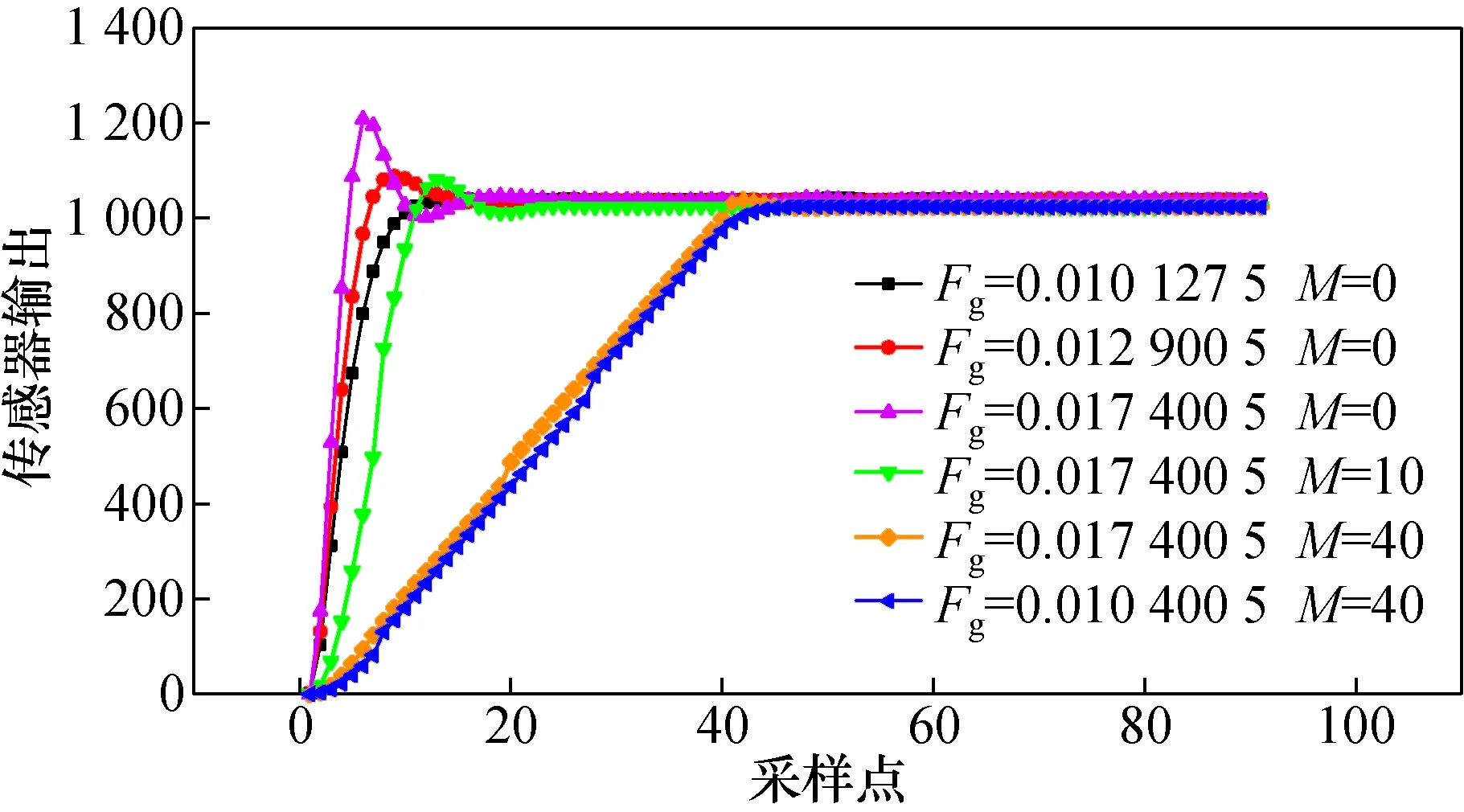
图9 实测光纤电流传感器阶跃响应Fig.9 Measured step response of fiber optic current sensor

4.2 频率响应测试

采用宽频功率源提供测试电流，最大输出电流为50 A，频率范围为45 Hz～10 kHz。

利用宽频精密分流器分流器和数字电压表测量电源输出电流，分流器在10 kHz下交直流误差优于60×10-6。电源输出线缆绕制5圈，光纤绕制8圈穿过线缆。被测光纤电流传感器采用光纤异步串行输出方式，通过光纤-以太网转接器将数据传入计算机，上位机测量程序同步采集光纤电流传感器输出及分流器输出，并进行比较，测试传感器频率响应特性。

图10 频率响应测试平台Fig.10 Test platformforfrequency response

实验设置不同前向增益及滤波器阶数测试光纤电流传感器频率响应特性，测试结果如图11所示。测试结果表明：增大前向增益可减缓传感器幅值衰减速度，提高传感器的带宽；滤波器的引入极大地限制了传感器的带宽，并且随着其阶数增加，该限制效果愈加明显。测试数据如表5所示，实测结果与理论计算基本一致。

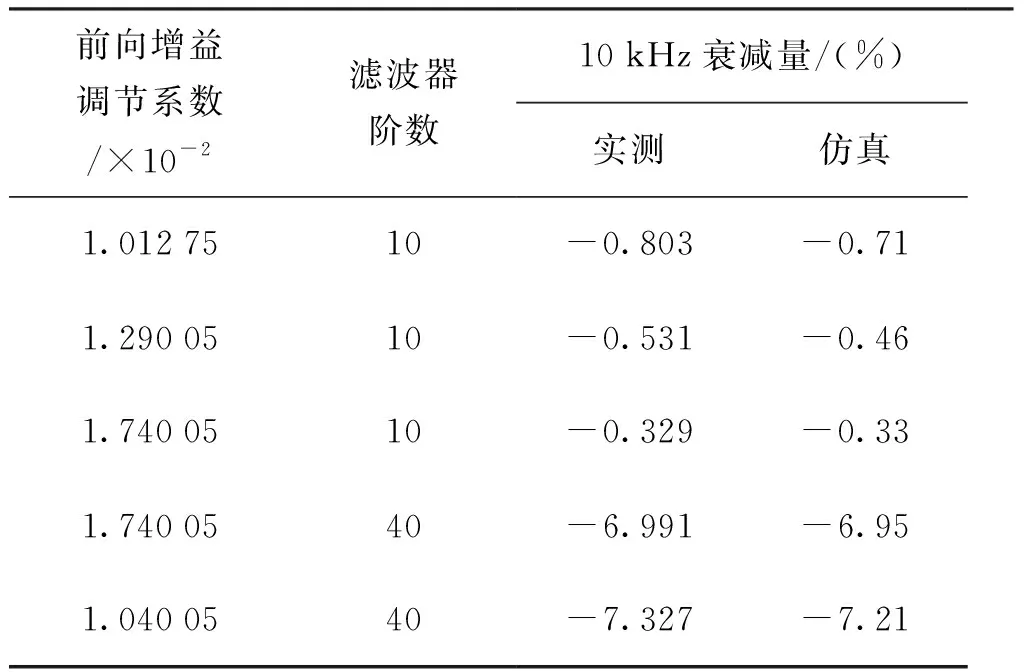
表5 光纤电流传感器实测频率响应指标Tab.5 measured frequency response index ofoptical fiber current sensor

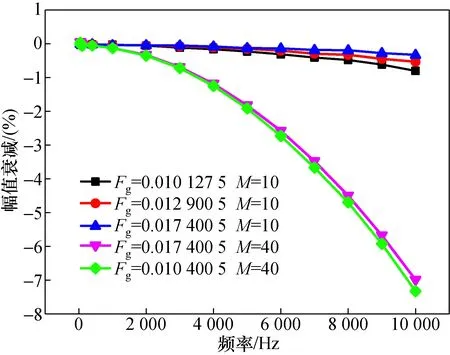
图11 实测光纤电流传感器频率响应Fig.11 Measured frequencyresponse of fiber optic current sensor

5 结 论

本文建立了传感器离散域高阶动态模型，基于Simulink对光纤电流传感器进行了仿真计算，并进行实验测试，得到如下结论：

(1) 由于前置放大电路、光电转换器、调制器驱动电路的引入，光纤电流传感器模型呈高阶特性，闭环系统反馈增益固定的情况下，前向增益的大小直接影响传感器的阶跃响应特性。

(2) 输出滑动平均滤波器对超调振荡具有显著的抑制作用，随着滤波器阶数的提高，抑制效果愈加明显，但同时也会延长上升时间及调节时间，降低传感器测量带宽。

(3) 本文提出的开环增益数字测量方法提高了传感器高阶动态模型的准确性，实测结果表明，仿真模型的上升时间、峰值时间及调节时间等参数与实测完全对应，阶跃响应超调量误差优于3.5%；10 kHz音频电流下，仿真与实测传感器衰减量误差优于0.15%。