俯仰式起重臂结构优化的解析算法研究

范开英，沈兰华，安玉振

（山东丰汇设备技术有限公司，山东 济南 250200）

俯仰式起重臂属于桁架式格构件，采用变幅机构进行旋转驱动，其结构形式在动臂塔式起重机、桅杆起重机和履带起重机等起重机中有较多应用。随着起重机性能需求的提升，特别是随着我国新能源领域的发展，起重机在起重量和工作幅度上都有较大提升，其设计方法[1]和计算精度也在不断改进。

俯仰式起重臂与固定臂不同，起重臂的计算结构模型随着幅度的变化而不断变化。受计算模型的限制，设计者通常在起重臂设计过程中选择极端工况进行校核，即选择最大起重力矩和最远端满载工况进行校核计算。

起重臂结构设计通常先将起重臂简化为单杆式轴心受压构件，通过力学三角模型进行轴力计算，此方式只能得到粗略的受力结果，对局部结构无法精确计算。通过工程图放样方法进行细部分析时，受经验和计算量等因素限制，难以得到起重臂设计的最优结构解。本文将探索建立起重臂载荷与幅度的解析算法，求解优化起重臂结构。

1 位置解析计算

俯仰式起重臂设计计算时，通过任意幅度B几何建模，求出起重臂扳起角度和变幅绳受力线角度，进而解析计算起重臂轴向载荷。

为精确计算起重臂受力，设起重臂长度为L，此长度为起重根部铰点O到起重臂头部起升定滑轮组J间的水平距离。在设计起重臂头部结构时，为增大吊装范围和布置滑轮组件，通常将起重臂头部结构设计成鹰嘴方式，而变幅滑轮组载荷作用点K通常也与起升定滑轮组位置不同。这些尺寸既直接影响起重臂的整体载荷，也间接影响起重臂的局部受力。图1 为起重臂结构载荷参数图。

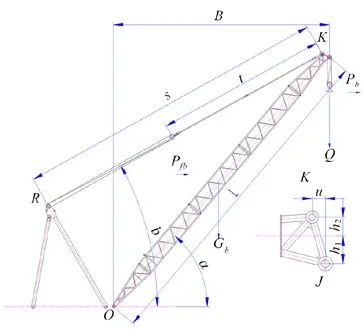
图1 起重臂结构载荷参数图

OJ的修正长度为

起重臂OJ轴线与水平面的夹角为

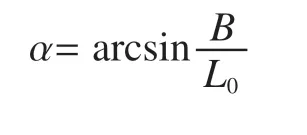
根据起重臂头部J和K结构几何关系，可求得当起重臂水平放置时，J、K两点之间的距离lJK和与竖直方向的夹角θKJV分别为

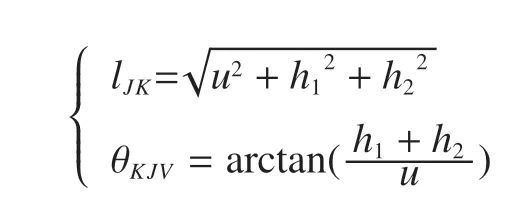
此时K点的坐标(XK，YK)为

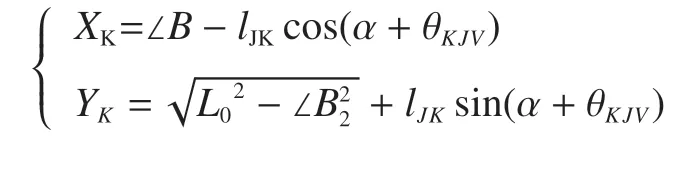
设人字架头部变幅绳铰点R为坐标为(XR，YR)，可求得变幅绳与水平面夹角为

在起重臂头部和人字架顶部中间悬空的变幅钢丝绳和变幅动滑轮组，随着计算工况的不同而发生相对位置变化。动滑轮组相对位置与幅度相关，为此建立几何模型，解析悬空部件的重量和位置与起升幅度的关系。起重臂头部变幅滑轮铰点K与人字架顶部铰点R间的距离s为

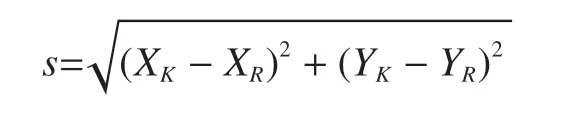
起重臂根铰点O到变幅力作用线的垂直距离lB为

2 载荷计算

起重臂载荷按方向分为竖直载荷和水平载荷，起重竖直载荷包括起升载荷Q和自重载荷Gt；水平载荷包括偏摆载荷Pb和变幅方向风载荷Pfb。起升载荷Q可通过读取起升性能曲线数据进行计算，自重载荷为方便计算，通常折算到起重臂头部积重进行分析。

头部积重载荷是起重臂载荷统计中最繁琐的载荷，需要考虑每一部分结构重量在起重臂头部的分配，通常这些载荷都是按照力矩进行分配的。设起重臂结构重心距离根部铰点距离为Li，起重臂自重折算到起重臂头部积重Qfb时为固定值

起重臂头部安装的定滑轮组、吊钩以及起升钢丝绳等机构部件始终跟随起重臂头部运动，可以直接汇总分项Qst统计到头部积重中。

如图1 所示变幅拉索（或拉板）的固定长度为t，设其单位长度自重为ql；变幅动滑轮组重量为GB；变幅钢丝绳倍率为n，变幅绳自重为qs；则此部分部件在任意作业幅度B时的折算头部积重分项QBt为

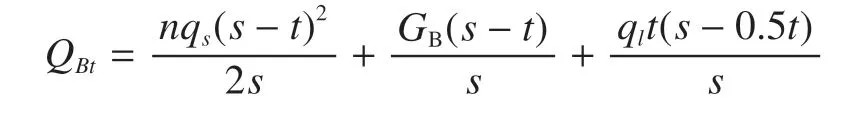
若空中有起升钢丝绳，可参照变幅钢丝绳的折算方法，同样折算到起重臂头部积重中，记为Qlt。

头部积重载荷汇总为

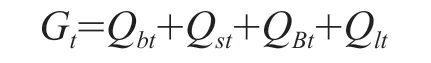
偏摆载荷Pb与和起重机回转速度有关，可按照起升载荷的偏摆角简化计算。工作风载荷风压为固定值，加载时与起重臂角度a有关，起重臂分节单部件计算时按照均布载荷计算，整体计算时按照力矩折算到起重臂头部0.5Pfb。

3 起重臂受力解析公式

起重臂载荷旋转力矩与变幅阻力矩相平衡，考虑自重冲击系数和起升动载系数的影响，由此求出变幅力FB为

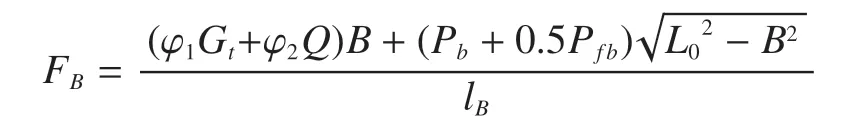
变幅力计算[2]分为起升变幅工况和起升回转工况。当计算回转工况时，水平力不在变幅平面内，则上述变幅力公式简化为

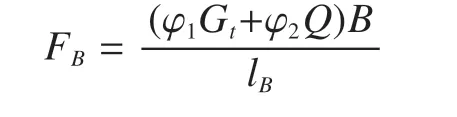
起重臂轴向力边对应的对角角度为π/2-β，变幅力边的对角角度为π/2+α，根据三角形正弦定理，起重臂轴力与变幅力与的关系为

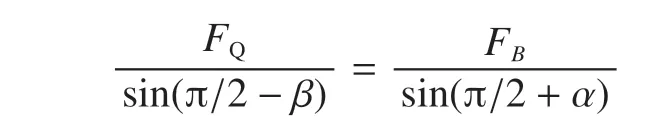
根据三角函数换算公式，由此得出起重臂轴向力为

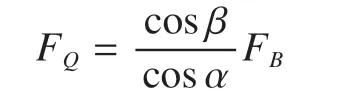
起重臂自重载荷为竖直方向上的均布载荷，在计算不同的截面位置分项载荷时，计任意点截面到起重臂根部铰点的距离为x，扳起后在任意截面处产生自重弯矩为

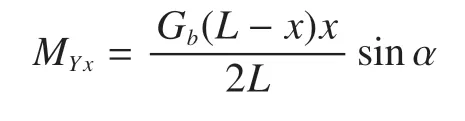
起重臂在回转平面内为刚性固定根部铰点端的悬臂结构。在回转工况中，回转方向风载荷Pfh为均布载荷，起升载荷的偏摆属于悬臂侧向载荷，则侧向弯矩为

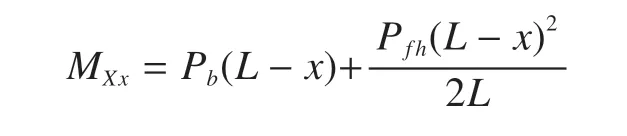
至此，起重臂任意工作幅度B，任意计算位置x处的载荷值，都可通过上述解析公式求得。

4 整体稳定性校核

动臂塔式起重机起重臂属于变截面受压构件，分段长度需要按照两端铰支对称变化构件的变截面长度系数 进行长度折算[3]。通常起重臂根部按照n=1 型式计算，起重臂头部按照n=2 型式计算。

在变幅平面内，起重臂为两端铰接约束的轴心受压构件，长度系数μ1=1。在回转平面内，考虑到起重臂头部有变幅绳的作用，对臂架的回转有保向稳定作用，可考虑稳定系数μ3。因此回转平面的计算长度按照如下公式进行计算

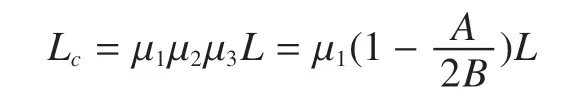
起重臂变截面部分转化为整体等截面格构式构件后，还要考虑腹杆截面积Af对整体结构的影响[4]，从而修正格构式组合构件的换算长细比 。

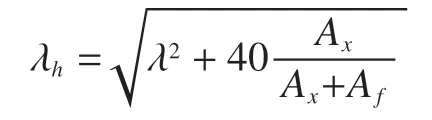
通过换算长细比查询稳定系数，校核压弯结构的起重臂，校核公式如下

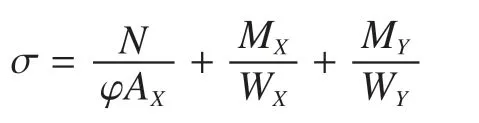
起重臂单杆的计算长度需要考虑没有腹杆支承侧的最大节间长度和材料的影响，其稳定校核比较简单，在此不再赘述。

在变幅平面内，起重臂为两端铰接固定的轴心受力构件，因此稳定性相对较好，起重臂根部通常设计成对称的桁架结构。在回转平面内，起重臂为悬臂压弯构件，整体折算长度较长，所以通常起重臂整体截面通常为水平方向更宽的矩形结构，有时会单独增大根部截面提升整体稳定性。

5 结构优化

由于起重臂头部结构的鹰嘴型式，起升载荷和变幅力作用线的交点通常不在起重臂轴向中心线上，此偏心距会给起重臂带来局部弯矩。随着起重幅度B的变化，起重臂轴和偏心距也会随之变化。此局部弯矩在起重臂头部值最大，沿着起重臂轴线逐渐减小，在根部铰点处变为零。

起重臂结构中心线和起重臂轴力线的偏角为

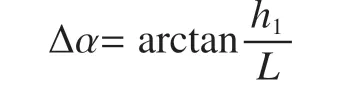
设起重臂根部铰点O为坐标原点，起重臂结构中心线方程为

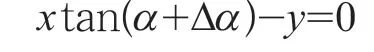
变幅力作用线与起升载荷幅度线交点的横坐标为B，纵坐标为

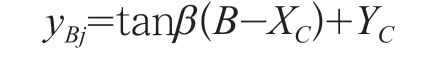
令k=tan(α+Δα)，则合力偏心力矩为

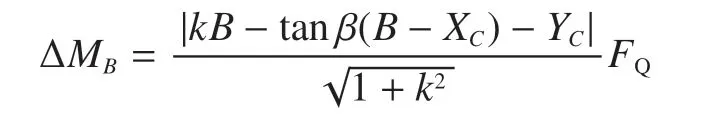
起重臂头部偏心力矩在结构设计时不可忽略，对头部结构的设计影响很大。在变幅平面内，起重臂头部通常不似根部结构设计成铰点型式，在需要起升定滑轮组向外偏心h2时，头部截面的高度h1和h2也需要加高来降低偏心距的影响。

随着起重作业幅度 的变化，起重臂头部偏心力矩也会变化，而且会出现顺时针到逆时针的方向变化，通过调整头部b的尺寸，可将两方向偏心力矩合理分配，改善起重臂头部受力。

6 结论

本文建立了俯仰式起重臂的几何解析模型，归纳了起重臂包括头部积重在内的分项载荷，提出了内力计算和整体稳定性校核的注意事项，并给出了起重臂载荷随幅度动态变化的解析公式，分析了头部几何结构对局部结构的受力影响，为起重臂的优化设计提供了理论基础。

1）俯仰式起重臂头部偏心结构不仅会影响整体载荷计算精度，而且会对头部结构产生较大偏心力矩，设计者需要在理论依据的基础上重点校核。

2）起重机工作幅度的变化，会影响俯仰式起重臂的结构参数和多项载荷，变幅阻力矩和头部积重是比较典型的代表。设计可通过工程图放样极端工况尺寸参数，也可通过建立联动方程进行精确解析，从而获得任意幅度的载荷变化。

3）通过系统分析起重臂载荷和内力，建立随幅度变化的解析计算公式，可充分校核起重臂各分段的应力安全系数，为起重臂结构优化提供了理论依据。