基于储能系统的独立光伏发电系统经济性分析

秦晓培

(国网河北省电力有限公司涉县供电分公司,河北 邯郸 056400)

0 引言

“十三五”期间,我国光伏行业得到了长足的发展。2016-2020年,全国光伏累计新增装机约1.07亿k W。随着“碳中和”战略的提出,光伏行业将迎来巨大的发展机遇,同时也面临着巨大的挑战。目前制约光伏大规模推广的主要障碍是光伏发电系统高昂的价格。世界各国都在进行各种试验以提高光伏电池的光电转化效率,进而降低成本。但是因为光伏系统经济性研究十分复杂,不仅涉及系统本身的初投资及技术可靠性,而且受到应用地区的生态环境、资源条件的影响,特别是其与随机性很大的太阳能资源和用户需求密切相关,因而研究工作更加困难[1]。目前,国内外大都采用实验示范研究、工程计算以及理论分析相结合的方法。实验研究的方法建立在大规模示范项目的基础上,但是需要投入巨大的资金,试验成本非常高。工程计算以及理论分析相结合的方法分为静态分析法和动态分析法[2]。

蓄电池储能是目前最成熟、最可靠的储能技术。但蓄电池存在循环寿命短、严格的充放电电流限制等一些难以克服的缺点,制约了独立光伏系统的大规模发展。蓄电池成本占系统造价的20%～25%,但由于光伏系统工作环境和工作过程的特殊性,导致蓄电池容量往往利用率较低,这进一步加大了光伏系统的成本[3]。因此合理优化选择蓄电池容量,对于降低光伏发电的成本、促进光伏系统普及应用有重要意义。储能蓄电池是光伏阵列和负荷的衔接点,静态分析法确定蓄电池容量是基于最长连续阴雨天数,只能静态地模拟蓄电池容量对独立光伏发电系统经济性的影响,考虑变量较少,在进行光伏系统经济性评价的过程中,忽略了使用地的环境条件等诸多因素,实践证明这些因素对光伏系统推广应用的成败起关键作用[4],图1为基于蓄电池储能的独立光伏发电系统结构。本文采用遗传算法定量地分析了太阳能光伏发电系统的经济性,不仅考虑了发电系统的静态成本效益,而且为其动态效益建立了以小时为单位的运行模型,包括太阳能辐射模型、太阳能电池板发电量模型、蓄电池模型和负荷模型,可实现对光伏发电系统的动态实时模拟,从而全面分析基于储能的独立光伏发电系统的运行状态。通过仿真计算得到了蓄电池容量最优解。结果表明,该计算方法能较为准确地求解蓄电池容量的最优解。

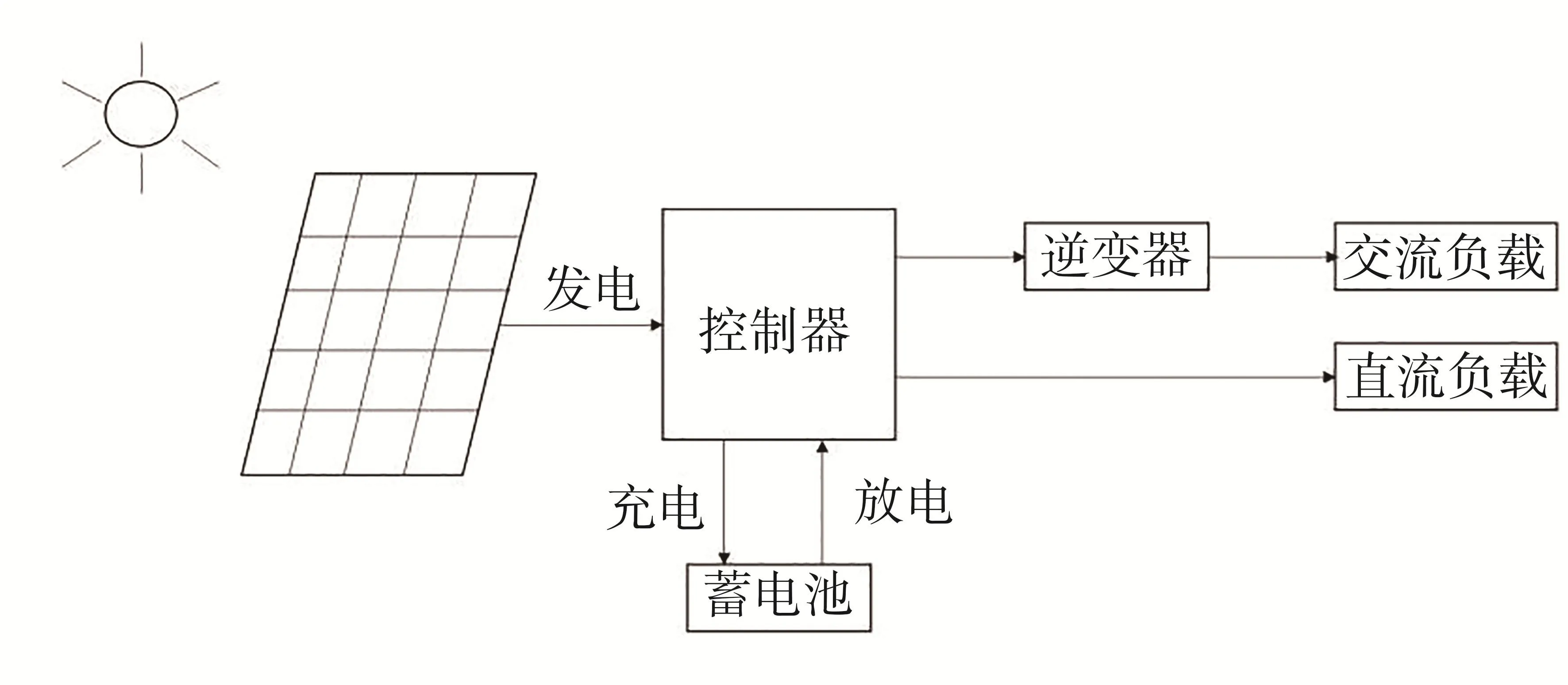
图1 独立光伏发电系统结构

1 光伏系统动态运行数学模型

1.1 太阳辐射值的计算

在进行太阳能光伏系统的设计过程中,太阳辐射值的计算非常重要,由于目前从气象观测站得到的太阳辐射数据大多是水平面上的观测值,在设计计算中,需要将水平面上的太阳辐射值转换为倾斜面上的太阳辐射值。

1.1.1 水平面日总辐射值

依据气象观测站得到的太阳辐射数据,可求得12个月中太阳总辐射值的日平均值分别为Hi,(i=1,2,…,12)。通过3次样条插值法来拟合太阳总辐射值的年变化曲线[5],在曲线中选取任意第n天对应的值,得到的就是第n天的太阳总辐射值。

1.1.2 基本参数

太阳赤纬角δ:日地中心之间的连线与地球赤道面间的夹角。这个夹角用如下公式表示[6]:

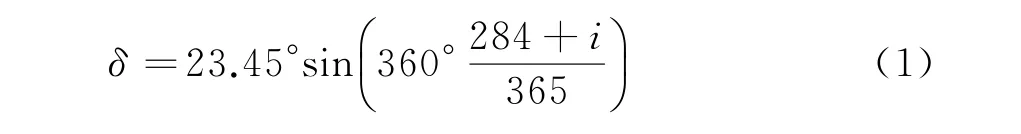
一日太阳光辐射时间Ni

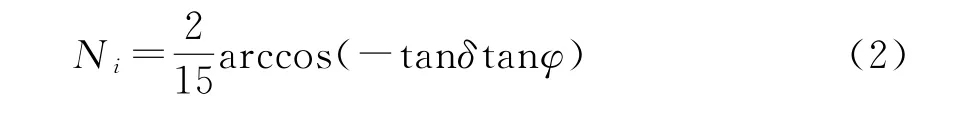
式中:i为从1月1日始到当年某天的天数;φ为朝向正南方向纬度。

日出时水平面上的角度ωs

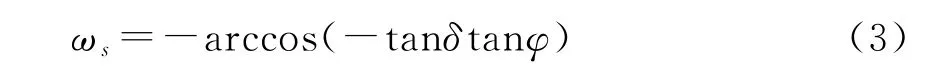
1.1.3 地球大气层外水平面太阳辐射值

日辐射量:一天中收到的太阳辐射量H'i,其计算公式为[7]:

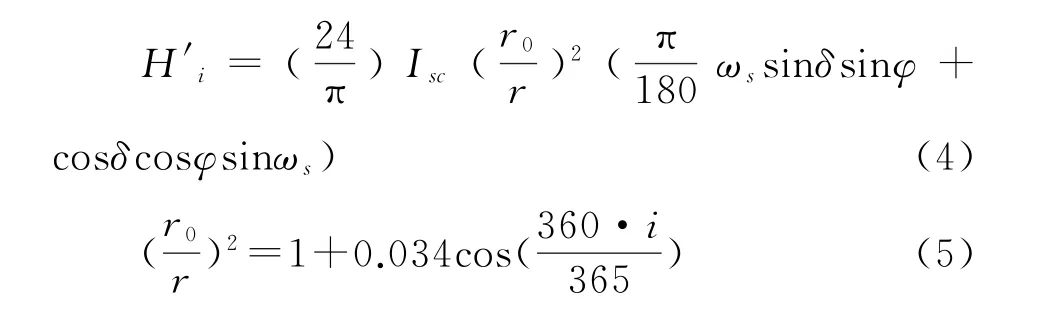
式中:r为某天日地之间的距离;r0为日地距离的平均值,大小为149 600 000 km;Isc为太阳常数,WMO1981年公布的值1 367 W/m2。

1.1.4 地球表面上倾斜面日太阳辐射量

气象观测站得到的通常是水平面上的太阳辐射数据,而光伏发电在实际应用中,一般是将太阳能电池板放在朝正南方向的倾斜面上。地球大气层外的南向倾斜面上小时太阳辐射量和水平面上小时太阳辐射量的比值可表示为[8]:

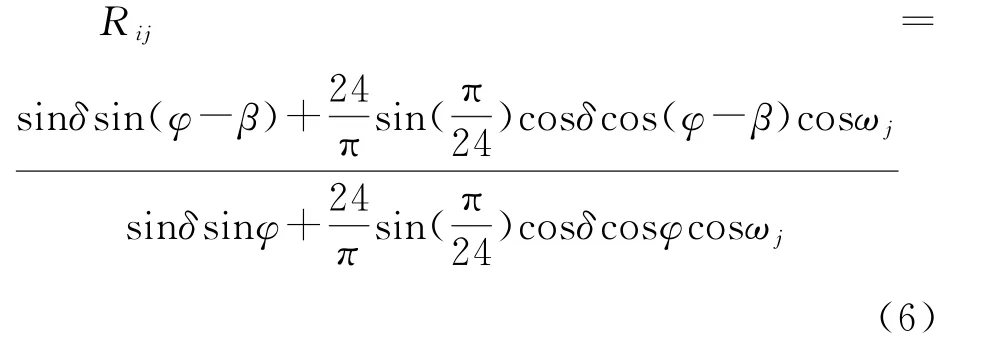
式中:β为斜面的倾斜角;j为一天24 h第某个小时;ωj为j时刻的太阳时角。

根据公式(6)可得到地球大气层外的倾斜面上的辐射量和水平面上辐射量的比值。考虑到太阳光在穿越地球大气层时,双方穿过大气层时受到的衰减程度相当,因此可以利用上述公式进行地球表面上的太阳辐射量计算。

1.1.5 地球表面上小时太阳辐射量

地球表面斜面上太阳辐射包括直射、散射和反射[8]。

考虑到一天中的小时太阳辐射量的变化与正弦曲线相似,可以将日太阳辐射量转换为小时太阳辐射量,水平面上小时太阳总辐射量表示为

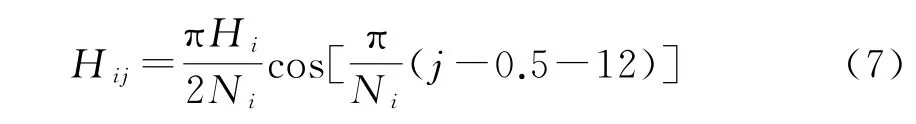
国外大量研究表明,地球表面上每小时的散射辐射量与总辐射量的比值同地球表面水平面上的日总辐射量与地球大气层外水平面上的日总辐射量的比值存在以下的关系

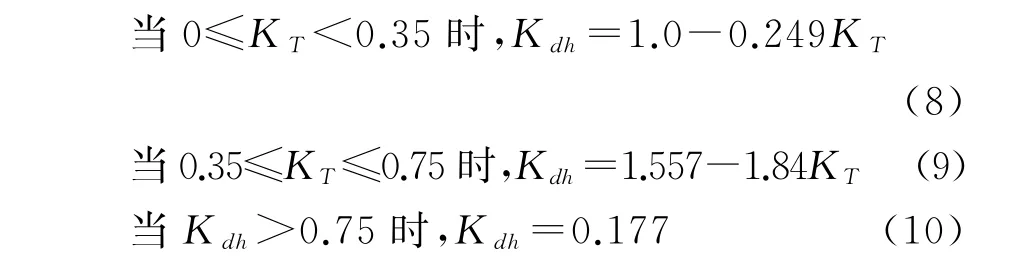
式中:KT为地球表面水平面上的日总辐射量与地球大气层外水平面上的日总辐射量的比值。

Kdh为地球表面上每小时的散射辐射量与总辐射量的比值

式中:ρ为地表的反射比。

使用特定一年的太阳光辐射数据的平均值,并为其添加随机变化使其遵循正态分布。

1.2 太阳能电池发电量模型

为建立合理的太阳能电池发电量模型,首先需要对太阳能电池方阵的发电量情况进行分析[9]。

1.2.1 方阵规模

在进行太阳能光伏系统的设计时,从太阳能电池组件铭牌可以得到该组件的关键参数:开路电压Uoc,短路电流Isc,最佳工作电压Um和最佳工作电流Im。在标准条件下,即在1 000 W/m2的太阳辐射强度下,根据负载所需的工作电压和功率的要求,选取X1个同一型号的太阳能电池组件进行串联,然后将X2组串联后的太阳能电池组件并联。组件总数N可表示为:

根据电路中电流和电压的特性可得以下公式

式中:U″oc、U″m、I″sc、I″m分别为在标准条件下整个方阵的性能参数值。

1.2.2 考虑温度和太阳能辐照强度的变化

根据标准条件下太阳能电池方阵的性能参数值,以及现有的实际太阳能辐射强度,温度计算实际情况下的太阳能电池方阵的性能参数实际值公式为

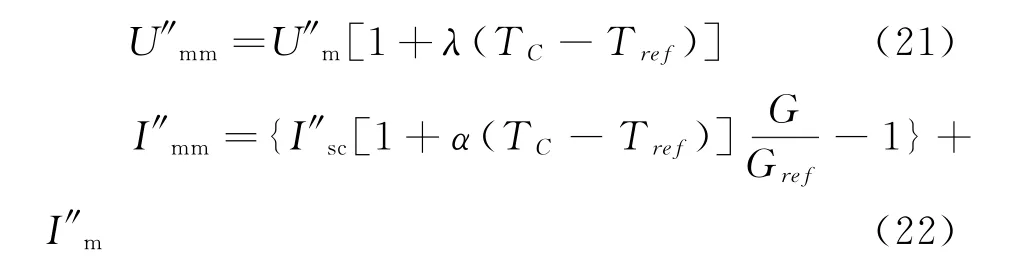
式中:α为短路电流Isc的温度系数;λ为开路电压Uoc的温度系数;G为实际的太阳能辐照度,W/m2;Gref为标准测试条件下的太阳能辐照度参考值,W/m2;TC为光伏方阵的表面温度;Tref为标准测试条件下的温度参考值;U″mm、I″mm分别为在实际情况下的太阳能电池的性能参数值。

1.2.3 温度模型

假设每天环境温度从极大到极小符合正弦曲线,于是有

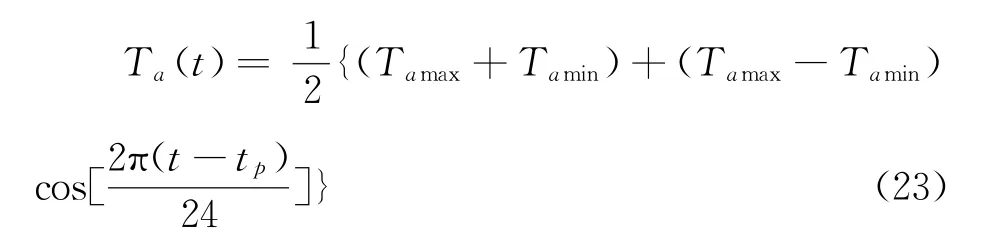
式中:Ta(t)为t时刻环境温度;Tamax为当天最高环境温度,也可近似取当月平均最高气温;Tamin为当天最低环境温度,也可近似取当月平均最低气温;tp为当地最高温度出现的时间;t为时间变量。

光伏方阵的表面温度可用太阳辐射能、环境温度和风速表示

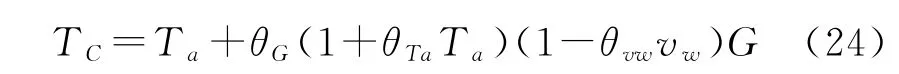
式中:TC为光伏方阵的表面温度,℃;Ta为环境温度,℃;θG为辐照度修正系数,θG=0.013 8;θTa为温度修正系数,θTa=0.031;θvw为风速修正系数,θvw=0.042;v w为风速,m/s;G为方阵面接收到的太阳总辐照度,W/m2。

太阳能电池的品种和封装形式都会影响以上几个修正系数取值。风速修正系数与方阵的安装形式和位置有关,往往需要根据实际情况作进一步修正。

1.2.4 太阳能方阵发电量计算

如何建立太阳能电池方阵的发电量模型是计算经济效益的关键。由(15)式可以计算得到南向倾斜面上此刻的太阳能辐射强度,将其代入(21)、(22)式计算可得到1 h中太阳能电池方阵产生的电量。将太阳能电池方阵产生的电量在一天中有太阳光照射的小时时间段进行积分,可得到一天中太阳能电池方阵产生的电量。

太阳能电池方阵的小时发电量计算模型:

太阳能电池方阵的日发电量计算模型:

1.3 蓄电池模型

蓄电池的电量保有状态函数:蓄电池电量保有状态随着每日负载耗电量及太阳能电池发电量的变化而变化。下面是根据蓄电池的电量变化得出的按小时计算的递推公式[10]

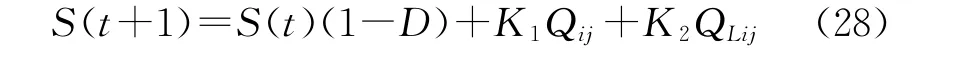
式中:D为蓄电池自放电率;Q ij为太阳能电池方阵的小时发电量;Q Lij为负载的小时用电量;K1为蓄电池充电效率;K2为蓄电池放电效率。

若考虑温度对蓄电池容量的影响(随着温度的升高,蓄电池的放电时间增加,放出容量增加,反之降低),引入温度修正系数ωT(把30℃时标准放电电流下的最大放电容量作为标准容量C N)[11]

式中:k为温度系数,是一个近似常数,一般取0.008。

1.4 负荷模型

负荷数据可从典型的住宅用电规律中选取,负载用有定值的矢量来表示。这个矢量代表了1 d中每个小时的用电量。图2显示了可能的1 d的实际负载值。

图2 典型居民住房24 h的实际负荷

用Q Lij表示具体每小时负荷值,如1 d负荷集合Q Li={Q Li1,Q Li2,…,Q Li24},k Wh。

2 求解方法和求解目标

2.1 遗传算法

常规的数学规划法一般有比较严格的收敛判据。遗传算法的收敛判据是启发式的,不需要梯度的信息。遗传算法使用概率机制进行迭代,搜索从群体出发,具有潜在的并行性,可以进行多个个体的同时比较。该算法使用评价函数启发,过程简单。目前采用的遗传算法收敛判据有多种,根据计算时间和采用的计算机容量的限制所确定的判据。如以最大遗传迭代次数作为收敛判据;从解的质量方面确定的判据,如连续一定次数得到的最优解无变化则认为遗传算法收敛,或最好解的适应值与平均值之差小于某一设定常数则认为算法收敛[5]。遗传算法计算流程示意如图3所示。

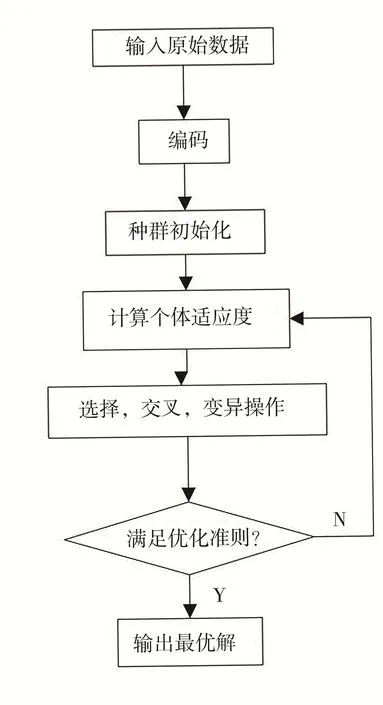
图3 遗传算法计算流程示意

2.2 目标函数的确立

经济分析在独立光伏系统设计中是不可或缺的一步,文中的效益分析中考虑了以下成本。

a.投资成本。通常太阳能面板和电池占了大部分的成本。本文假定太阳能电池板大小已知,所以只考虑蓄电池成本。

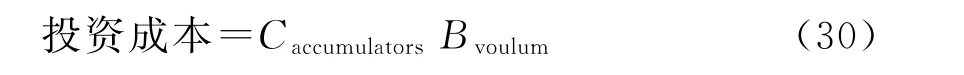
式中:Cbattery为蓄电池单位容量投资成本;Bvoulum为蓄电池容量。

b.断电的成本损失。除了投资成本,与能量损失或中断相关的成本也应该被考虑。

式中:n为断电次数;Coutage为单位断电损失(元/outage);Plost为总的能量损失,k Wh;CkWh为用户能源中断损失(元/k Wh)。

Coutage和CkWh可以根据往常的运行经验获得。

c.负荷用电量效益。

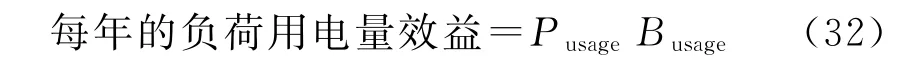
式中:Pusage为负荷用掉的电能,k Wh;Busage为从1 k Wh的电能中获得的效益,元/k Wh。

在本文中,Busage假定是和从电力公司购买一样的价格。

d.盈余电量损失。电池板发出的电量没有被蓄电池储存,也没有被负荷用掉的部分为盈余电量,其浪费是投资的一种损失。

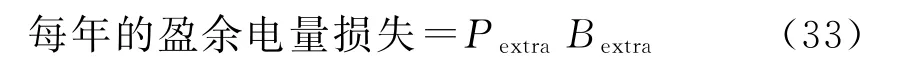
Pextra为太阳能电池板发出却未被使用的电能,k Wh;Bextra为1 k Wh的电能所包含的潜在效益,元/k Wh。Bextra可用太阳能电池板的等值单位成本效益表示。

根据以上分析,与蓄电池大小应用相关的总成本Ctotal:

Ctotal=投资成本+断电的成本损失+盈余电量损失-负荷用电量效益

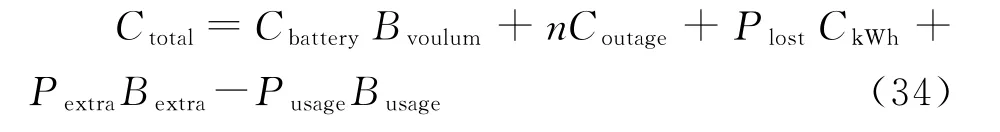
则本文的目标值是Bvoulum,目标函数为Ctotal。

3 太阳能系统动态模型过程验证

3.1 太阳能系统动态运行拟合过程

过程实现图例流程示意见图4。

图4 过程实现图例流程示意

3.2 太阳能系统动态模型参数设置

3.2.1 月总太阳辐射值

本文以广东地区广州为例,气象站太阳能总辐射值取自中国气象科学数据共享服务网,资料起止年代为2001-2010年,为累年数据平均值。各月总太阳辐射平均值H i(MJ/m2)数据列入表1。

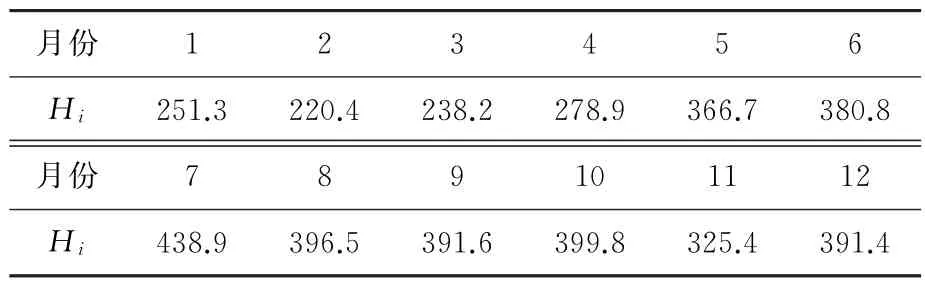
表1 月总太阳辐射平均值 MJ·m-2

3.2.2 纬度、反射比

广州的地理纬度为23.1°,地表反射比设定为0.2。

3.2.3 太阳能电池板参数

本文拟采用型号为NES71-5-185M的单晶硅太阳能电池板,测试标准为1 000 W/M2,25℃,标称功率185 W。相关其他参数如表2。

表2 太阳能电池板参数

3.2.4 太阳能电池板串并联数

本文给定太阳能方阵中电池板的串联数为10,并联数为20,则总标称功率为37 k W。

3.2.5 温度

温度模型参数亦取自中国气象科学数据共享服务网的地面气象数据,资料起止年代为2001-2010年,为累年数据平均值。广州地区最高温度出现时间由近日天气预报数据拟合,设定为15点。月平均温度列于表3。

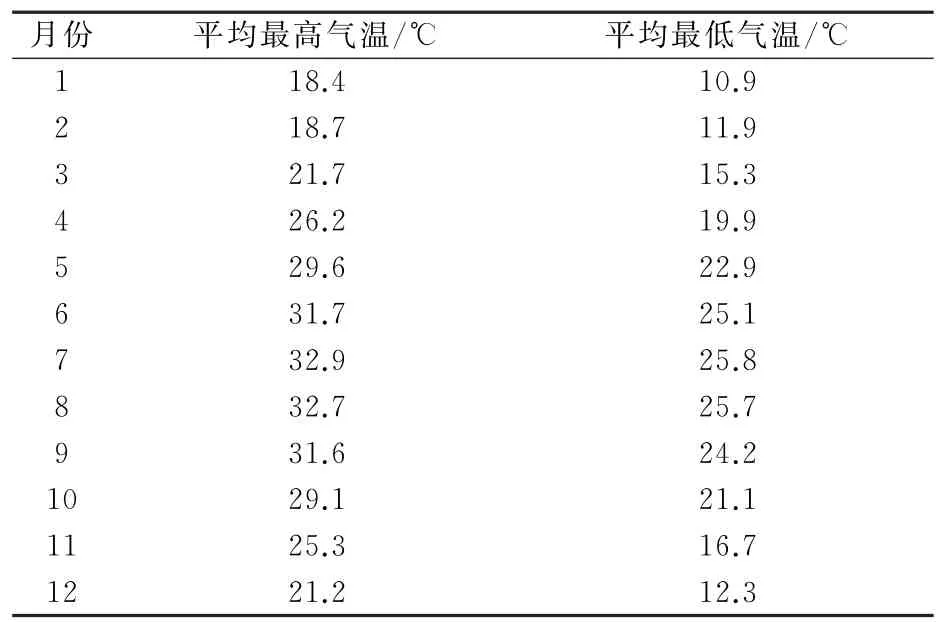
表3 月平均最高最低温度数据

3.2.6 太阳能电池板倾角

其中太阳能电池板倾角1,2,3,11,12月时采用倾角23.1°,4～10月时采用倾角为7°。

3.2.7 蓄电池

本文分析的蓄电池假设采用型号LCXA12100AH,标称容量为12 V×100 Ah=1.2 k Wh。售价为820元/块。

3.2.8 负荷

负荷模型本文采用全年统一的负荷模型,模型数据Q Lij(k W)根据太阳能发电量和普遍用户负荷规律估测确定。

3.2.9 运行分析

参数设定如下:蓄电池的成本为685元/k W,断电恢复耗费发电系统的成本1元/h,用户能源中断损失为1元/k Wh,用户用电效益为2元/k Wh,盈余电量损失为2元/k Wh。

3.3 仿真结果分析

采用3次样条差值拟合得到的一年太阳辐射曲线如图5所示。

图5 一年每天的日总太阳能辐射曲线

假设太阳能系统采用最大功率MPPT跟踪装置,使太阳能电池板运行在最佳工作点,可得到图6所示的每天的总太阳辐射值。

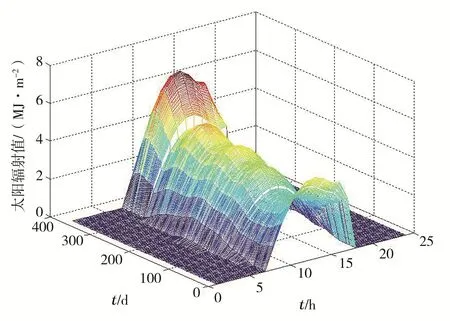
图6 小时太阳辐射能

由图6可以看出,太阳能电池板一年的动态小时发电量受到太阳能辐照度变化的影响较大,见图7。

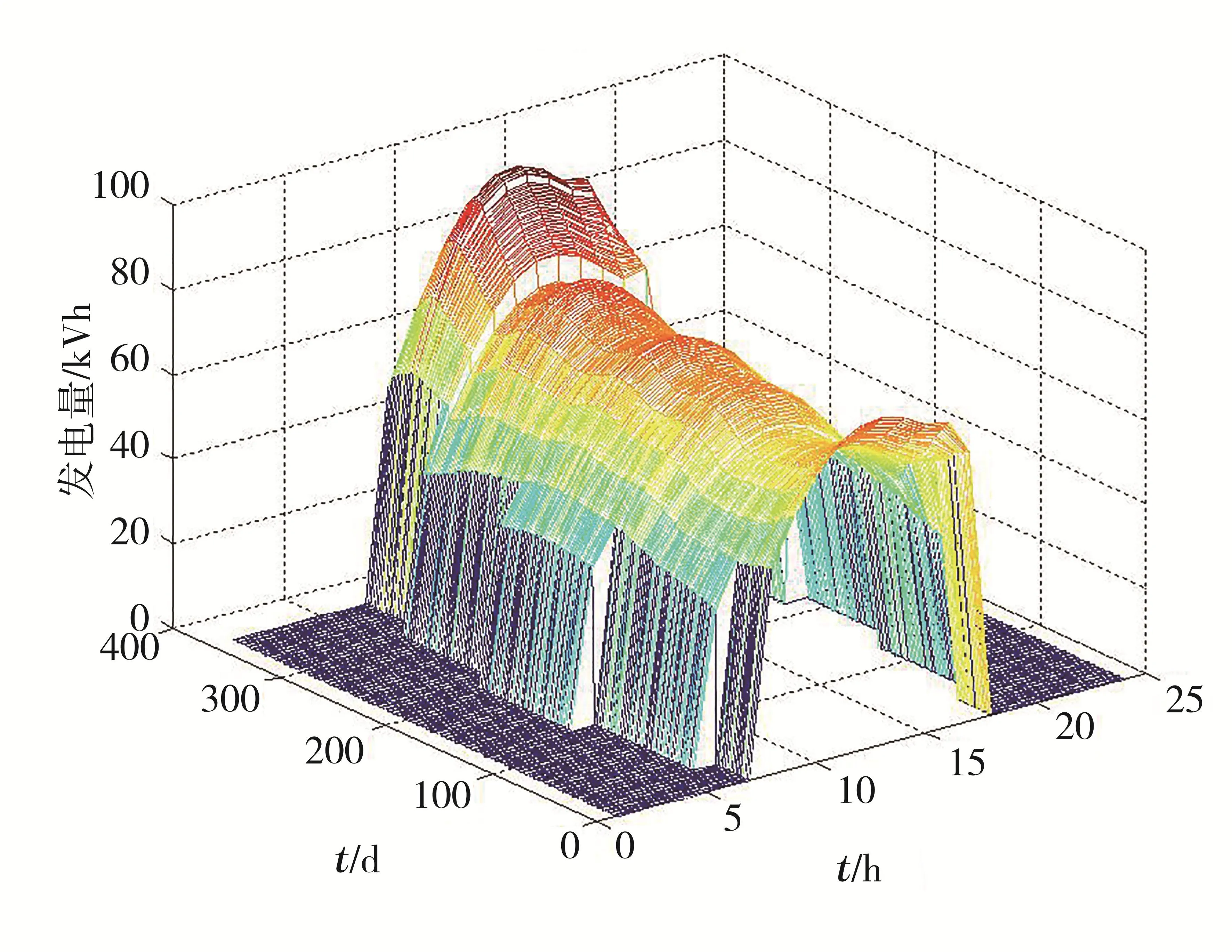
图7 一年内小时太阳能电池板发电量

由图7可以看出,一年内小时太阳能电池板发电量集中在07:00-18:00,在14:00左右达到最大。运行得到的负荷模型对应的日负荷曲线如图8。由图8可以看出,一天中09:00以后负荷数逐渐增大,晚上20:00左右达到最高,符合预期。文中模型可以得到较为准确的日总太阳能辐射曲线、小时太阳能电池板发电量以及日负荷变化规律,证明了该数学模型的可靠性。

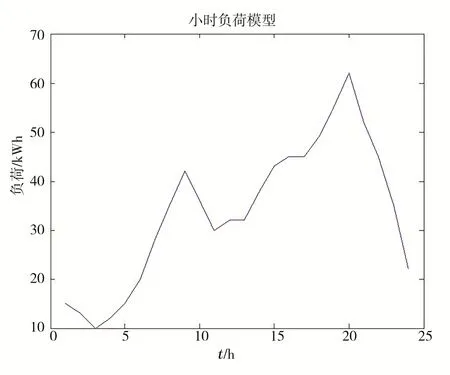
图8 日负荷模型

4 实例的经济性分析

4.1 遗传算法的实例计算

以太阳电池储能为例:如果用电器功耗为1 k Wh/d,考虑到连续阴天的可能性,则储能蓄电池的总容量一般要求5 k Wh,即5 d内只要1 d有阳光,就能保证5 d内连续正常供电;而太阳电池组件的装机功率至少需1 k W,100%发电效率的光照时间达到5 h才能将蓄电池充满电。由于光照时间和强度因不同地区而异,晴天条件下,达到100%发电效率的光照时间通常在3～6 h。因此独立系统和独立电网的光伏发电,发电组件的功率与储能电池通常以1∶5左右配备。

本文为使取得的最优解更可靠,配备蓄电池的最小容量Bvmin以不配备为准,即功率为零,配备蓄电池的最大容量Bvmax按发电组件功率的30倍计算,解空间的取值范围[Bvmin,Bvmax]。本文中Bvmin=0 k Wh,Bvmax=1 110 k Wh。

本文采用最大迭代次数为运行终止条件,最大迭代次数为200次。

4.2 最优解结果分析

4.2.1 实际拟合最优解

将[Bvmin,Bvmax]以步长为1 k W依次计算Ctotal,所得结果如图9所示。因此本文的最优解近似为BVolume=298 k Wh。Ctotal=-271 053.515 2元。标称容量为12 V×100 Ah=1.2 k Wh,即需要249块蓄电池,一年内除去成本还可赚取271 053.515 2元。太阳能电池板和蓄电池配置比例为1∶8.05。

应用最优解得到的运行过程缺电量和用户用电量如图10-11所示。图10-11实现了全年动态模拟过程显示,可见此最优解尽量保证用户用电量的同时,在相应运行过程也有缺电量的存在,因而也就减少了浪费的电量,最大程度保证了蓄电池容量的充分利用。因此此最优解在经济上是合理的。

图10 运行过程缺电量

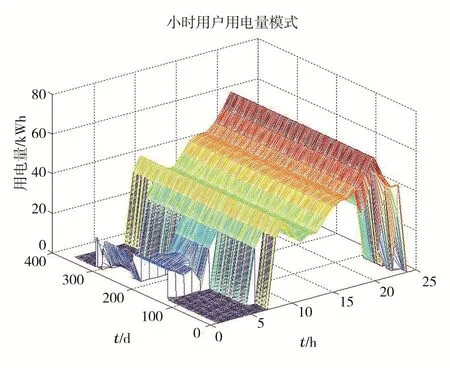
图11 用户用电量

4.2.2 遗传算法最优解

改变变异率和迭代次数,进行多次仿真试验,试验结果见表4。

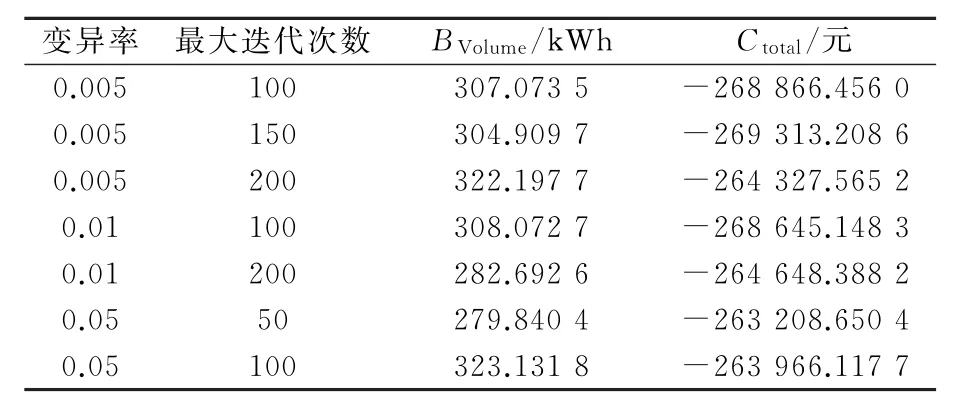
表4 改变变异率和迭代次数试验结果

当改变[BVmin,BVmax]为[250,350]时,所得结果见表5。

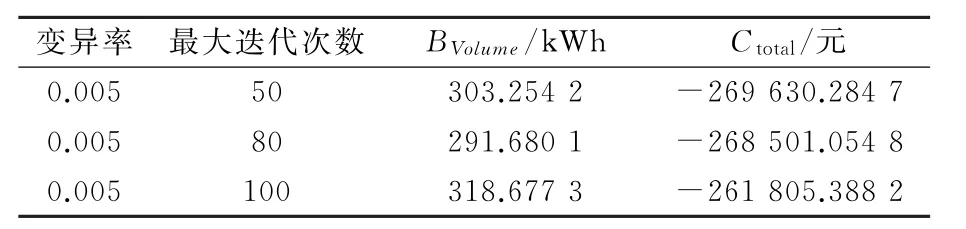
表5 改变寻值区间和迭代次数试验结果

在表4和表5所示的仿真计算中,应用遗传算法最大迭代次数为100时,BVolume=307.073 5 k Wh,Ctotal=-268 866.456 0元。最大迭代次数为200时,BVolume=322.197 7 k Wh,Ctotal=-264 327.565 2元。不同的最大迭代次数对应的2个最优解BVolume和Ctotal绝对值相差均小于5%。改变寻值区间,BVolume和Ctotal绝对值最大相差也小于5%。证明该遗传算法收敛,该仿真模型计算结果具有较高的精度。

5 结论

本文在光伏系统发电成本制约发电系统普遍推广的背景下,研究了基于储能的光伏发电系统经济性分析问题。本文建立了以小时为运行单位的独立的光伏发电系统的各部分模型。包括太阳能辐射模型、太阳能发电量模型、蓄电池模型、负荷模型,对基于储能系统的独立光伏发电系统进行了仿真计算,可以动态模拟独立光伏发电系统的运行过程。本文还建立了以储能为变量,包含蓄电池成本、太阳能电池板电量浪费损失、系统断电损失、用户用电效益为变量的目标函数。采用遗传算法计算分析了蓄电池容量的最优解。结果显示该计算方法能较为准确地求解蓄电池的最佳容量。