基于数据驱动鲁棒优化的区域综合能源系统运行调度策略

徐澄莹,杨 军,张宇威,朱 旭

(武汉大学电气与自动化学院,湖北 武汉 430072)

0 引言

在迫切需要改善能源结构的当今社会,新能源和电动汽车等的引入使电力系统源荷不确定性相关的综合能源管控主动响应技术研究成为了目前热门的课题。

鲁棒优化是在历史数据区间集中寻找最恶劣环境下的最优策略的方法,它往往会趋向过于保守的方案。随着大数据、物联网的发展,越来越多测量设备接入能源系统,储备了大量的数据,包括光照、风力等气候数据,以及人群用能数据等。这些数据都可以作为综合能源系统对负荷和能源进行预测、调度的资料。用数据驱动方法挖掘数据的深层关系能够更好地兼顾系统的经济性与安全性,也使综合能源系统更好地成为数字化主动电网的一部分。

目前常用的盒式数据驱动鲁棒优化方法[1-4]存在以下问题:忽略了源荷数据间的相关性,使策略考量中纳入了许多实际不存在的场景;子问题需经过对偶转化的盒式模型,求解过程较复杂;大多文献中综合能源系统建模仅考虑电、热2种能量形式。

本文提出的模型采用数据驱动MVEE算法构建椭球不确定集,可以更好的描述光伏与负荷间的关联性;采用基于极限场景的列与约束生成法求解各个极限场景下的调度策略,无需对子问题进行对偶化;建立了电、热、冷、气相互转换的综合能源不确定性问题调度模型。首先建立了含有电、热、冷、气的区域综合能源系统日前-实时两阶段调度模型,其次进行了数据驱动MVEE椭球不确定集的构建,然后使用列与约束生成法求解了调度模型,最后采用比利时Elia电网数据进行算例分析,证明综合能源管控与电力大数据技术的优势。

1 区域综合能源系统两阶段调度模型

1.1 区域综合能源(RIES)系统结构

RIES系统结构如图1所示,在本文中的RIES系统,由上级电网、分布式光伏发电站向系统供电,燃气管网向系统提供燃气。电热锅炉、蒸汽轮机、P2G设备、空调、吸收式制冷机为可控设备。热分配系统将燃气锅炉、电热锅炉产生的热以及热储能合理分配给热负荷和吸收式制冷机。P2G产生的天然气将合理配给系统内锅炉自用和售出给燃气网。同理,多余的电量也将售回电网。系统中的电、热储能增加了系统消纳光伏能量、维持系统平衡的能力。由于光伏发电以及用户端用电具有随机、间断的特点,使系统中具有了源荷不确定变量。

图1 RIES系统结构

1.2 系统调度目标函数

本文提出的优化模型,旨在使运行成本最小的同时弃光率尽可能小。因此目标函数如下:

式中:C total为最终的总运行成本;C DA为第一阶段日前调度成本;C RT为第二阶段实时调度成本;x是日前调度中的决策变量;代表了综合能源系统中的随机变量(光伏出力和电负荷);y是实时调度中的决策变量。

在本模型中,将燃气锅炉与蒸汽轮机视为热电联产整体,统一以CHP下标作为标识。由于在目标函数中,热电联产机组、电热锅炉、电转气、电热储存设备、空调的各个表达式形式完全相同,因此下文中均以mach为下标的式子进行统一表述,具体展开只需改变下标即可。式(2)中,C mach是热电联产机组、电热锅炉、电转气、电热储存设备、空调的基点出力成本;C DApgrid为日前阶段购售电成本;为日前阶段购售气成本。

式中:T为整体的调度周期时段数;Δt为调度周期内的单位时间;a mach、b mach为热电联产机组、电热锅炉、电转气、电热储存设备、空调的发电成本系数;P mach为热电联产机组、电热锅炉、电转气、电热储存设备、空调的基点出力;P buy、P sell、G buy、G sell分别为日前购售电量和气量。在本文中,气量均换算为天然气完全燃烧产生的热能进行计算和描述。λDApb、λDAps、λDAgb、λDAgs分别为日前购售电、气单价。

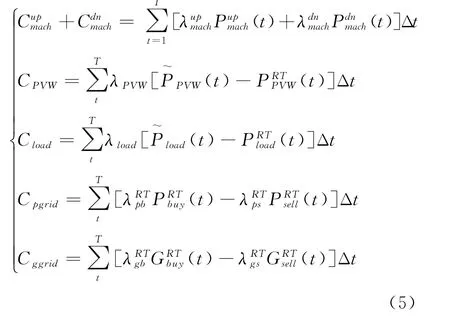
1.3 日前调度约束

1.3.1 能量平衡约束

式中:PCHP(t)是热电联产机组的基点出力;Pout(t)、Pin(t)是 电 储 能 放 电、充 电 功 率;Pbuy(t)、Psell(t)是与上级电网购售电的功率;是光伏和负荷的预测功率;PP2G(t)、PEB(t)、Pcond(t)是电转气、电锅炉和空调的电功率。

式中:HCHP(t)、HEB(t)、Hout(t)是热电联产机组、电热锅炉和热储能功率;Hload(t)、Hin(t)是热负荷和热储能充热的功率;Hcold(t)是分配给吸收式制冷机的热功率。

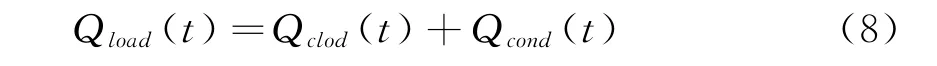
式中:Qload(t)为冷负荷需求;Qclod(t)、Qcond(t)是空调、吸收式制冷机的制冷功率。

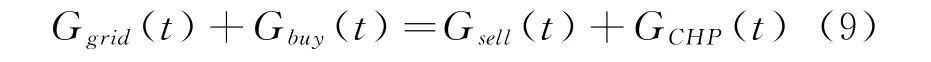
式中:Ggrid(t)是电转气设备产出的天然气量;Gbuy(t)、Gsell(t)是向上级气网购售气的量;GCHP(t)是热电联产机组的耗气量。以上变量单位均为功率单位,是将天然气转换为相应完全燃烧热后的数值。

1.3.2 能量耦合设备运行约束

式中:ξCHP是热电联产机组的用能效率系数;ζP是热电联产机组产能分配给电能的比例系数;OCHP是控制热电联产机组开关的零一变量;是热电联产机组运行功率上下限;是热电联产机组上下爬坡极限。P2G设备约束与其基本相同,不多赘述。

式中:ξcold是吸收式制冷机的转换效率系数。

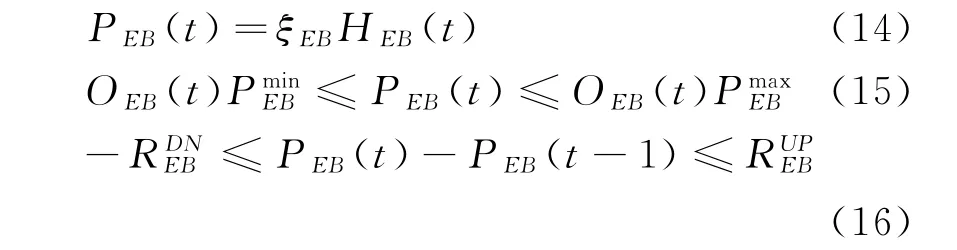
式中:ξEB是电热锅炉的用能效率系数;OEB是控制电热锅炉开关的零一变量;PminEB、PmaxEB是电热锅炉运行功率上下限;RDNEB、RUPEB是电热锅炉上下爬坡极限。空调约束与其形式相同,不多赘述。

1.3.3 储能设备约束

储能在同一时间不可以同时处于充、放能2种状态。

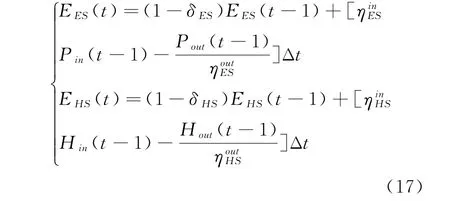
式中:δES、δHS为能量在电、热储能设备中的自损耗系数;为电热储能在充放能时的效率。另外要求储能量、充放能功率在约束范围内,电、热储能设备的初始状态和末时段状态的储能量统一,公式不多细表。

1.3.4 购售电气约束

要求购能和售能不允许在同一时间进行,购售量不超过电能联络线功率交互极限和输气管道的最大流量(换算为功率单位)。

1.4 实时调度约束

1.4.1 功率调整约束

由于约束内容与日前调度十分相似,仅需将以上公式中电气设备变量P替换为P+Pup-Pdn即可,不多赘述。另外添加设备功率上下调整约束如:

1.4.2 弃光、切负荷约束

允许系统在实时阶段产生弃光和切负荷,以保证系统的安全运行。

1.5 日前-实时两阶段鲁棒优化模型

由本节以上部分,可以得出鲁棒两阶段模型如下:

式中:x为日前调度的决策变量,X为其可行域,c(x)为日前调度成本函数;y为实时调度决策变量,Y为其可行域;为随机变量,U为不确定集;其余字母皆代表了1个实系数矩阵。

本文所建模型为min-max-min模型,内层min为实时调度成本最小问题,max函数则是寻找最恶劣环境,外层min函数计算日前、实时调度总成本最小问题。

式(20)中,x,y具体内容如下:

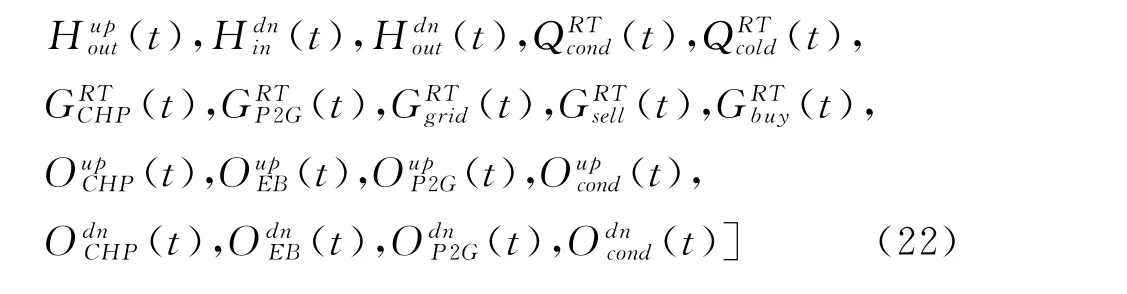
2 数据驱动椭球不确定集构建

2.1 构建方法

下面介绍本文使用的数据驱动不确定集构建方法[5]:

a.将光伏出力、负荷需求历史数据放于一个集合内。

b.构建高维椭球集合。

一个以对称正定矩阵A和中心定点c代表的全维椭球E可以用如下数学方法描述:

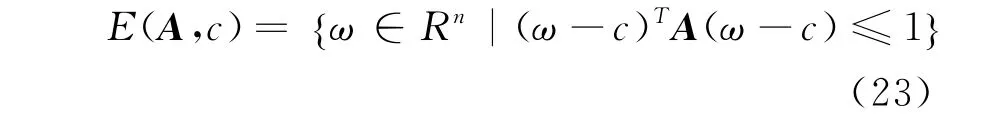
提出问题式(24)来求解椭球最小体积,确定A和c的值:

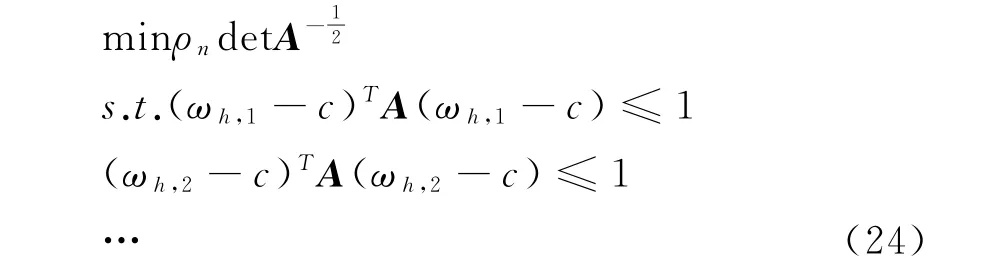
c.使用lift-and-project KY-1方法求解(24)得到椭球集合[6]:

用2个NP+NL维的最小体积椭球来包裹某一时间段的所有场景集合,一个是NP+NL维的场景集 [W(1),W(2),…,W(Ns)]∈R(NP+NL)×1,另一个是偏差集合 [ΔW(1),ΔW(2),…,ΔW(Ns)]∈R(NP+NL)×Ns。由此,整个问题可以被描述为如下的优化模型:

式中:p为集合中的数据点。使用文献[7]提出的lift-and-project KY-1方法进行求解,将原来(NP+NL)×N s维的集合ω提升为(NP+NL+1)×2Ns维的集合ω':

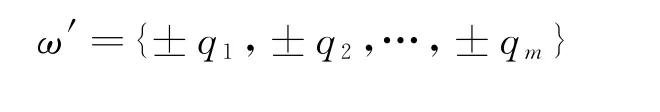
式中:ω'与ω的中心点是相同的,我们可以由ω'组成的新问题MVEE(ω')(27)的解得出 MVEE(ω)的解。

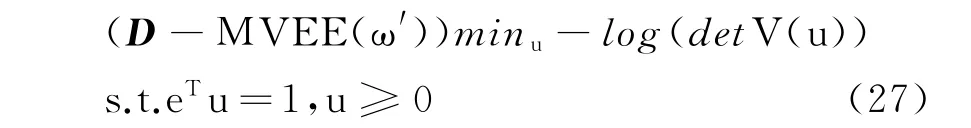
随后通过求得的u和ω',原问题可以用下式解出:

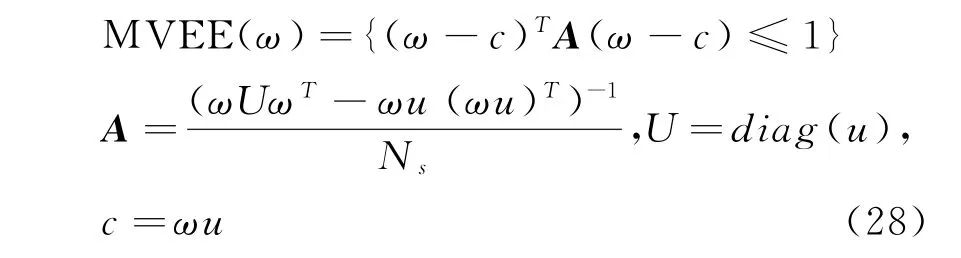
d.求取顶点坐标(极限场景)。通过式(29)的转换,将椭圆平移为轴向椭圆E',从而求取顶点坐标

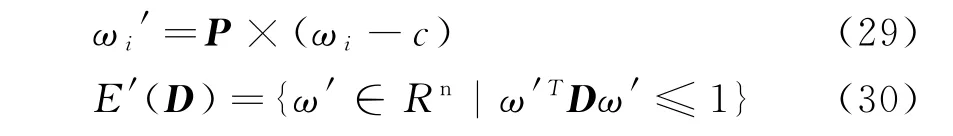
式中:ωi、ωi'分别为原椭球场景和变换后轴向椭球场景;P是用于正交分解A=P T DP的正交矩阵;D是A的特征值对角阵;E'是变换后得到的轴向椭球。

可以通过变换后得到的轴向椭球顶点坐标(31)用坐标变换(32)得到原椭球的顶点坐标:

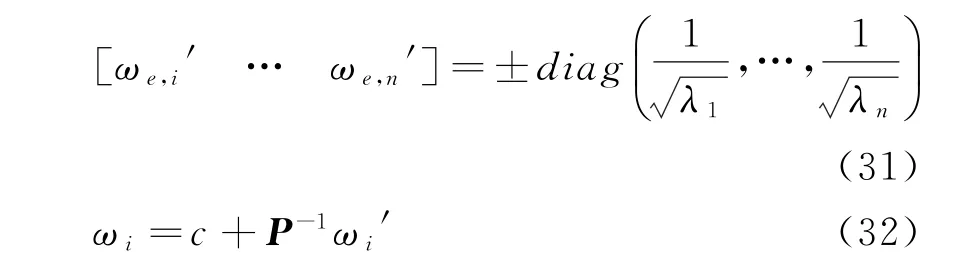
由于凸优化问题中极值一定出现在可行域的顶点处[89],所以求得的椭球顶点即为极限场景。

2.2 仿真构建

摘取比利时Elia电网2021年1—3月每日07:00-18:00整点光伏与电网负荷的数据[10],为使其矩阵便于在MATLAB中求逆,将为0的数据加上一个极小的值。

由于实际不确定集为一个24维的椭球,难以通过二维图片展示,所以将选取单一时段的不确定集数据作图。

如图2所示,图中黑点为某一时段的历史场景,红点为MVEE算法得出的极端场景,绿色椭圆则是根据极端场景绘制的椭球集合。以这组数据为例,盒式不确定集会将椭球的右上和左下空白部分也包括在内,这种将不存在的场景考虑在内的方法增加了不必要的保守性。而椭球集可以调整自身轴的长度和角度精确包括场景[11],且数据间的相关性越强,其精确包含场景的优越性就越明显。

图2 基于极限场景法的椭球集合(12:00)

3 模型求解

3.1 问题分解

将原两阶段模型分解为主问题和子问题如下:

3.1.1 主问题

主问题为在多个极限场景下的最优日前调度策略,其数学描述如下:

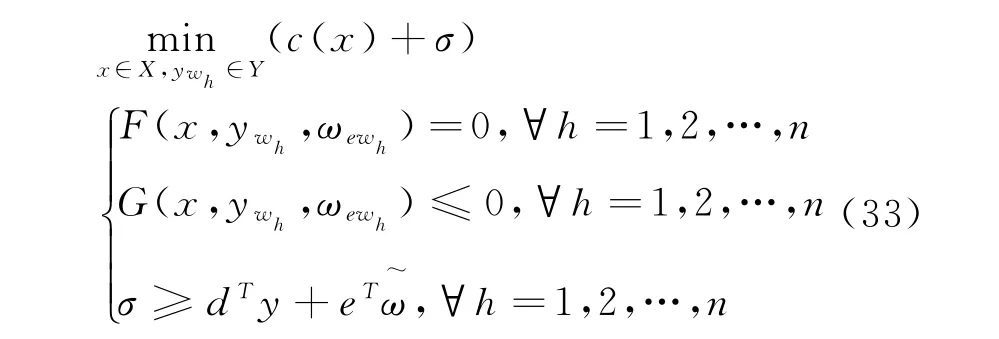
式中:n为列与约束生成法的目前迭代次数;σ为在主问题极限场景中的实时调度最大成本;y w h,ωew h分别为极限场景w h下的实时决策变量和随机变量。

3.1.2 子问题

子问题是求解在当前日前调度策略下,所有极限场景中最恶劣的情况(最高成本),并将最恶劣场景中的约束条件添加到主问题中,进行迭代。

式中:是第n次迭代主问题求出的日前调度策略。

3.2 迭代求解

基于列与约束生成法迭代交替求解主问题与子问题,其步骤如图3所示。

图3 CCG算法迭代流程

初始化设置上下界值分别为正负无穷,求解主问题更新下界,求解子问题更新上界,若判断收敛则结束循环;若不收敛则更新目前最恶劣环境,继续迭代。

4 算例分析

4.1 数据选取

4.1.1 源荷预测数据

取自比利时Elia电网2021年4月13日07:00—18:00的电网预测数据和光伏预测数据。

4.1.2 电价及天然气价格

由于天然气和电的价格在不同时间和地点均有不同,根据文献[12-15]中所估算的价格范围,仿真选取的天然气购入价格在0.295～0.465元/k Wh(换算为电功率),售出价格在0.24～0.375元/k Wh范围内浮动;购入电价在0.245～0.415元/k Wh,售出电价在0.19～0.325元/k Wh范围内浮动。

4.1.3 设备运行数据

根据文献[14]设置汽轮机、电锅炉、电转气和空调的上下功率调整成本为0.3元/k Wh。根据文献[15],设置切负荷成本为6元/k Wh,弃光惩罚成本为0.6元/k Wh。

根据负荷和光伏的发电量,设置系统各设备的容量如下:光伏1 000 k W,CHP 8 000 k W,电转气4 000 k W,电热锅炉6 000 k W,空调5 000 k W,电热储能8 000 k W,电气管道线路传输功率300 k W。

4.2 仿真过程

本次仿真使用MATLAB R2017a软件、YALMIP以及GUROBI求解器进行模型仿真及求解。模型求解迭代如图4所示。

图4 模型求解迭代示意

图中蓝色线条为主问题求解得出的下界值,红色线条为子问题得出的上界值。仿真代码共进行了6次迭代,在第5次迭代时,上下界值相同,结果收敛求解完成。日前调度成本为8 314.194 1元,实时调度成本361 918.792 6元,总调度成本370 232.986 7元。

4.3 仿真运行分析

4.3.1 日前运行

日前电功率运行情况如图5所示。

图5 日前电功率运行情况

由图5可见,在07:00—09:00光伏发电量不足时,为了满足电负荷需求燃气轮机增加了其输出功率。同时,电转气机组也随之加大运行,以满足燃气轮机对燃气的需求。电储能设备适时放出储备电量帮助缓解用电需求并将产生的多余电量存储起来。

购售电方面,仅向上级电网购入少量电能,未有多余电量售出。可见系统基本实现了极大的电能自我产生与消纳能力,对外界的依赖较少。日前热功率运行情况如图6所示。

图6 日前热功率运行情况

由图6可知,电转热设备的功率运行兼顾了热负荷与冷负荷的需求,其功率大小基本与热负荷需求曲线同步。热电联产机组的余热曲线与电能的产生曲线一致。热储能设备达到了削峰填谷的作用。热功率中有相当一部分供给了吸收式制冷机。这是因为吸收式制冷机是一种运行成本十分低廉的冷功率产生设备,其在冷热功率之间的转换损耗极低,可以有效省去空调制冷带来的成本。日前冷功率运行情况如图7所示。

图7 日前冷功率运行情况

在图7中,除了由于07:00—09:00热储能放出了较多热量,导致分配给吸收式制冷机的热量过多,造成了一定浪费外,其余部分的冷功率需求均为恰好。我们可以看到运行周期内的冷功率需求几乎均由吸收式制冷机提供,仅在17:00—18:00余热不足时使用空调制冷。日前天然气用量情况如图8所示。

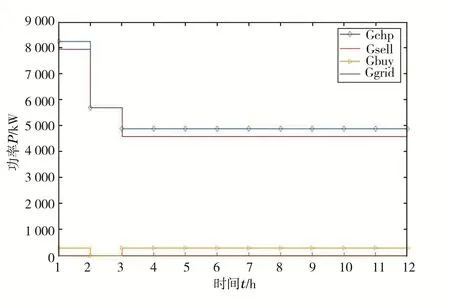
图8 日前天然气用量情况

从图8可以看到,天然气的消耗设备在07:00—09:00用量较大,这是由于此时的光伏发电量还不足以满足负荷需求,需要消耗天然气来产生电能。绝大多数的天然气需求均由P2G设备提供,只有少量需求是依靠向气网购气满足的,系统中没有产生多余的气量售出。这也证明了系统内部对各种能量相互转换和消纳的能力较强,对外界能量的依赖性低。

4.3.2 实时功率调整分析

总体而言,实时功率调整结果会相较于日前策略更保守,这是因为实时调整会考虑在所有历史场景中满足约束条件,所以会采取更加稳定的出力方案对应不确定性因素的干扰。

由于篇幅原因不将所有设备功率调整情况列出。实时电热锅炉功率调整情况如图9所示。

图9 实时电热锅炉功率调整情况

从图6可以看出,电热锅炉在07:00—08:00功率较小、产热不足,而在其余时段均有着很高的功率。所以在图9实时运行中,对其功率进行了调整,增加了07:00—08:00时的功率,减少了其余时段过高的功率,使其更符合实际运行需要。实时空调功率调整情况如图10所示。

图10 实时空调功率调整情况

由图10可知,由于早上07:00余热较少,所以空调增加了制冷功率来填补吸收式制冷机的功率空缺,满足负荷的稳定性。但是总体上,空调的使用率依然较低,保证了系统运行的经济性。

4.3.3 不确定集选取方法对比研究

为了证明本文提出的数据驱动椭球不确定集的鲁棒优化方法可以有效提高系统运行经济性,本节将其与传统盒式鲁棒调度模型进行对比验证。不确定集方法成本对比见表1。

表1 不确定集方法成本对比

由表1可知,利用数据驱动MVEE算法确定的椭球不确定集可以有效地降低运行成本。尤其是在实时调度中,由于传统盒式不确定集没有很好地描述源荷数据相关性,导致其将许多实际不存在的情况纳入了考虑范围,从而增加了成本。

而数据驱动不确定集在保守性与经济性中取得了良好的平衡,既保证了系统在最恶劣环境中的正常运行,又降低了整体的运行成本。

5 结论

以综合能源系统的调度问题为研究内容,针对如何通过不确定集的选取方法来平衡系统的保守性与经济性这一问题,通过综合能源管控的主动响应技术以及电力大数据的主动管理技术,研究并验证了数据驱动的椭球集的优势。本文得到的主要结论如下。

a.建立了包含电、热、冷、气的综合能源系统调度模型,描述了综合能源系统中能源产生、相互转换的原理和方法。

b.建立了数据驱动不确定集,通过仿真验证了其有利于描述数据相关性与减少实际不存在场景,验证了电力大数据技术的优越性。

c.通过建立日前-实时综合能源系统鲁棒优化模型,使用列与约束生成法简化模型迭代求解。对模型进行了仿真分析,验证了综合能源管控的主动响应技术的优越性。