基于曲率分布控制的叶型前缘设计方法

童歆，羌晓青，虞培祥,3，欧阳华,3,*

1.上海交通大学 机械与动力工程学院，上海 200240 2.上海交通大学 航空航天学院，上海 200240 3.燃气轮机与民用航空发动机教育部工程研究中心，上海 201306

压气机作为燃气轮机的核心部件，通过高速旋转的叶片对空气做功以提高空气压力，要求在逆压梯度的环境中组织流动，尽量减少能量损失。因此压气机叶型的气动性能对压气机的工作效率有着重要影响。叶型前缘段虽然在长度上只占叶型很小一部分，但其设计形状对叶型整体气动性能的影响却举足轻重[1]。学者们对于叶型前缘设计的研究也在不断深入。

20世纪60年代，Group和Carter[2]通过试验研究发现更尖锐的前缘有更宽的许用攻角范围。1991年，Tuck[3]用奇异摄动法理论推导了翼型前缘分离的近似判断准则，认为前缘发生流动分离的临界攻角与前缘点曲率的平方根成反比。Cumpsty和Walraevens[4]通过试验研究了圆弧形前缘和椭圆形前缘的类压气机平板绕流在不同攻角、雷诺数和来流湍流度下的变化。发现带椭圆形前缘的平板相比圆弧形前缘能有效推迟分离泡的产生，减小分离泡尺寸。同时，来流湍流度对分离泡和边界层的发展有较大影响。Wheeler等[5]在低速单级高压压气机试验台上研究了前缘几何形状对尾流/边界层相互作用的影响。结果发现有/无尾迹时，椭圆形前缘相比圆形前缘都能推迟边界层的转捩，从而减小损失。Elmstrom等[6]以NACA65(12)10翼型为对象，用CFD仿真对比研究了翼型前缘无涂层、有均匀涂层或非均匀涂层对空气动力学性能的影响。结果显示涂层会导致前几个弦长百分比位置处压力梯度的改变，从而产生分离泡，并可能导致边界层转捩的提前发生。2011年，Goodhand和Miller[7]首次提出用尖峰扩散因子Dspike来定量描述吸力面的前缘吸力峰。通过优化设计“无尖峰前缘”，减小尖峰扩散因子，能够有效抑制前缘分离和诱导转捩，实现损失的降低和许用攻角范围的拓宽。在他们的研究结果中认为，尖峰扩散因子在叶片的入射角范围内保持在0.1以下，则叶型性能不会受到前缘几何形状的影响。于贤君等[8]用三维数值模拟方法研究了圆弧形、椭圆形和曲率连续前缘对叶型附面层发展的影响规律。结果表明不同前缘造型使得前缘Spike不同，过强的前缘Spike使得速度型不饱满，更难以抵抗逆压梯度而导致分离泡和提前转捩的发生，致使边界层增厚，叶型损失增加。白涛等[9]在前缘形状对涡轮叶栅损失的研究中也发现椭圆形前缘相比圆弧形前缘能更好地抑制吸力峰的产生，且椭圆长短轴比越大效果越明显。

相应地，许多学者开展了新型前缘造型方法的研究。陆宏志等[10-11]发展了一种易加工的带平台的圆弧形前缘，数值模拟与流动试验的结果显示：其特有的双吸力峰强度远弱于圆弧形前缘的单吸力峰，有一定的抑制流动分离效果。Kulfan[12]引入形状类别函数变换技术(Class/Shape function Transformation technique, CST)，对叶型形状进行参数化表示，使得叶型厚度分布在转换空间里可以进行完全平滑解析的设计。刘宝杰等[13-14]对形状类别函数变换法进行改进,提出了MCST方法，消除了设计工况下的前缘速度尖峰，使叶片气动性能得到改善，并发现使用不同的形状函数生成的曲率连续前缘可用攻角范围差别很大。崔涛等[15]改善CST造型方法并将之应用到涡轮叶片的前缘修型中，获得了消除HD叶型吸力面前缘分离泡和推迟分离诱导转捩的良好效果。Korakianitis等[16-17]在设计涡轮叶片时提出在构造的抛物线中弧线上添加曲率连续的多项式厚度分布造型方法，该方法能保证前缘曲率及曲率导数连续，在涡轮叶片上的应用结果显示其能有效优化前缘流动。宋寅和顾春伟[18-19]用基于三次Bezier曲线构造的曲率连续前缘探究了曲率连续性对压气机叶片前缘流动的影响，解释了前缘曲率连续性对叶片性能的影响机理。施恒涛等[20]提出了基于多项式的曲率连续造型方法对前缘形状进行优化，大幅降低了前缘吸力峰，增强了抗分离能力，避免了边界层的提前转捩。

上述的几种造型方法及其应用结果已经证明保证曲率连续性的前缘几何造型相比传统的圆弧形前缘有更好的气动性能。同时，前缘的曲率分布特别是前缘点的曲率大小对于前缘流动和边界层的发展有直接而敏感的影响，因此通过调整曲率分布来优化叶型的气动表现应该成为前缘设计中必须考虑的一点。上述的造型方法通过保证衔接点的连续性确定造型参数来进行前缘设计，曲率分布只能在造型设计完成后通过曲线参数或曲线坐标反求得到，不利于在考虑曲率影响的前缘设计时的迭代优化。因此本文发展了一种基于控制曲率分布的前缘造型方法，实现了对叶型前缘曲率的直接、精确控制。将该方法使用在某可控扩散叶型(Controlled Diffusion Airfoil, CDA)的前缘造型上，探究了在保证叶型前缘曲率连续性的情况下，曲率分布如何影响叶型性能——特别是对前缘分离泡和分离诱导转捩的影响。

1 造型方法

1.1 基于曲率分布控制的叶型前缘造型方法

在如图1所示的坐标系下考察，将原点置于叶型前缘点处，x轴沿叶型前缘几何进气角方向。A、B两点分别为前缘段与吸力面(Suction Side,SS)主型线、压力面(Pressure Side,PS)主型线的衔接点。以吸力面侧前缘段的造型为例,用n+1点p阶Clamped节点分布的B样条函数来描述该段曲线的曲率沿x方向的变化：

图1 造型方法参考坐标系

(1)

式中：Ni,p(u)为p次B样条基函数；P=[xK]T为曲率分布控制坐标，其中P0=[0K0]T、Pn=[xnKn]T分别定义了前缘点和衔接点处的曲率，衔接点处的曲率等于吸力面主型线上该点的曲率以保证曲率连续。此时曲线弧长的微分表示为

其中:k=dy/dx表示曲线斜率，其对应的角度定义为φ=arctank，可以导出

根据曲率半径的定义，微分弧长对应的微分角度满足关系：

可以导出关系：

(2)

记f(u)=K(u)|x′(u)|，对式(2)两端在[0,u]上进行定积分可得

(3)

这样就得到了曲线斜率的规范参数化表达。然后通过积分可以得到曲线的纵坐标:

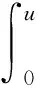
(4)

曲率连续前缘曲线需要满足的约束中，曲率和横坐标的连续性已经由首尾2个控制点所满足。为保证斜率连续，由式(3)可知应满足

(5)

同时，为保证曲线终点落在衔接点处应满足

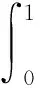
(6)

因此在曲率分布给出后，只需要使曲线同时满足式(5)和式(6)2个约束即可得到满足曲率分布的造型曲线。曲率分布与对应的生成曲线示意如图2所示。

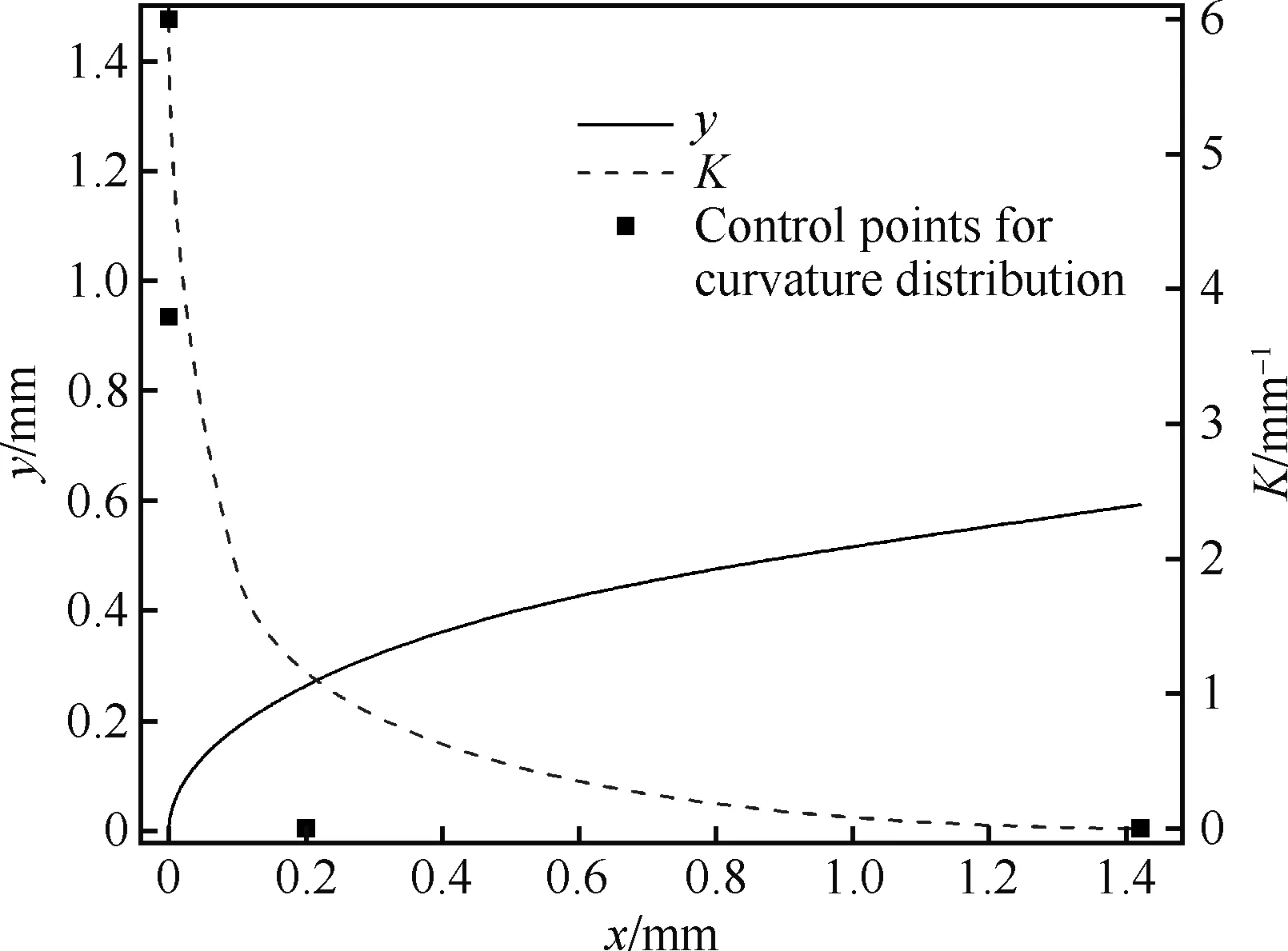
图2 曲率分布与对应曲线形状示意图

在此方法中，对于控制曲率的分布，因为采用了B样条曲线的数学描述，使得在式(3)的计算中右端积分项始终为比较简洁的高次多项式形式，于是斜率k(u)可以用解析方法表达出来。在求解确定参数及逐点生成曲线的过程中，仅有式(4)中的数值积分会带来一定误差，且该误差在逐点确定曲线轮廓的时候是不会累计增加的。实践中该项误差可以维持在前缘尺寸量级的10-8以下。因此可以认为该方法有较高的精度，特别是相对于基于曲率离散差分的方法。

需要注意的是，曲率分布采用的B样条曲线表达形式也会对最后生成的叶型形状产生影响。一般来说，更多的控制点意味着更大的设计自由度，可以满足更严格的、更高阶的连续性条件。但在阶数上，高阶表达式容易导致曲线形状失真振荡。因此建议曲率分布表达式阶数p≤3，控制点的数目可以根据要求控制的曲率分布复杂程度适当增加。在进行前缘设计时，只需要根据前缘曲率分布对叶型损失，特别是转捩位置的影响规律，构造合适的曲率分布函数，便可以方便地得到最优的前缘造型设计。

1.2 研究对象

研究对象为某工业级压气机叶片50%叶高处可控扩散叶型，采用了比较原始的圆弧形前缘。考虑到目前工程设计中已经很少采用圆弧形设计，而一般使用椭圆形前缘，因此为贴近工程实际，构造椭圆形前缘作为研究的基准(Baseline)叶型前缘，其基本几何参数由表1给出。

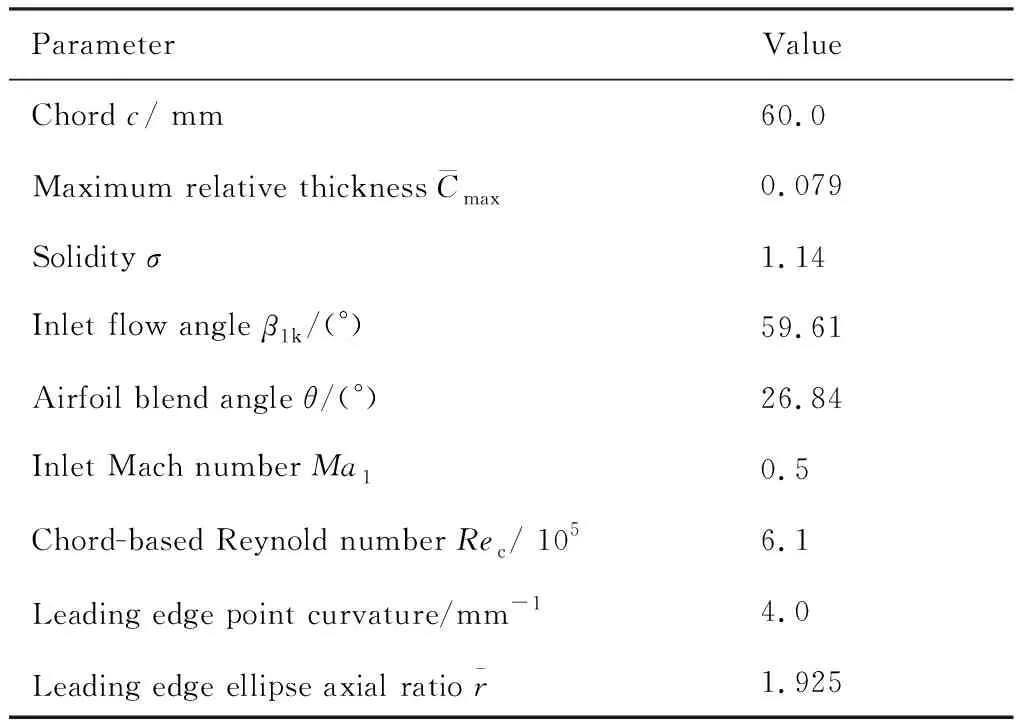
表1 基准叶型参数

采用1.1节所述的造型方法对该基准叶型前缘进行重新设计。本文中进行前缘造型的区域为叶型前2%(中弧线)弧长范围，许用攻角范围内前缘吸力峰位置均位于该区域，2%弧长后主型线曲率变化幅度很小且变化速度缓慢。

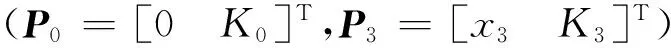
图3所示为基准叶型和设计得到的4种前缘形状和曲率分布(吸力面侧)的对比。因为吸力面和压力面与前缘连接点处的位置并不完全对称，斜率和曲率也不相等，所以压力面侧的曲率分布准确来说与吸力面侧有所不同，但对本研究叶型而言相差很小，其大致形状与曲率分布与图3所示基本一致。第1组的曲率分布差异主要体现在前缘点处的曲率值大小，第2组的曲率分布差异主要体现在靠近前缘点处曲率沿x的下降速度，Baseline(椭圆弧前缘)下降最快，K4次之，K4B几何前缘点处曲率下降最慢，分布相对“饱满”。此外Baseline的曲率分布在下降至接近平缓时存在一处不连续的突变。

2 数值方法

采用ANSYS CFX商业软件的k-ωShear Stress Transport(SST)湍流模型进行雷诺平均数值模拟(RANS)仿真计算，同时采用γ-Reθ转捩模型捕捉流动中的转捩过程。边界层转捩的预测对平面叶栅气动性能的计算有重大影响，γ-Reθ转捩模型在文献[21-23]中应用于叶轮机械流动,均获得了比较理想的结果。计算上采用高精度的对流格式，设置进口总压为110 841 Pa，进口总温为310.775 K，出口静压为103 270 Pa。叶高方向设置对称性(Symmetric)边界条件。进口湍流度为5%。稳态计算的收敛标准为通量残差的均方根值(RMS)小于10-6。

本仿真计算中采用了HOH型拓扑网格，如图4所示。叶片壁面网格膨胀比设为1.1，保证y+<1以满足湍流模型和转捩模型对边界层网格的要求。为了更好地捕捉前缘分离和转捩的流动情况，在叶片前缘处及相邻的压力面和吸力面附近加密流向网格。考虑到网格质量对计算湍流和转捩过程的重要性，本文通过对比4种不同规模网格进行了网格无关性验证。各套网格的参数如表2 所示。图5给出了全攻角总压损失系数的计算结果，图中i为攻角。总压损失系数定义为

图4 二维计算网格

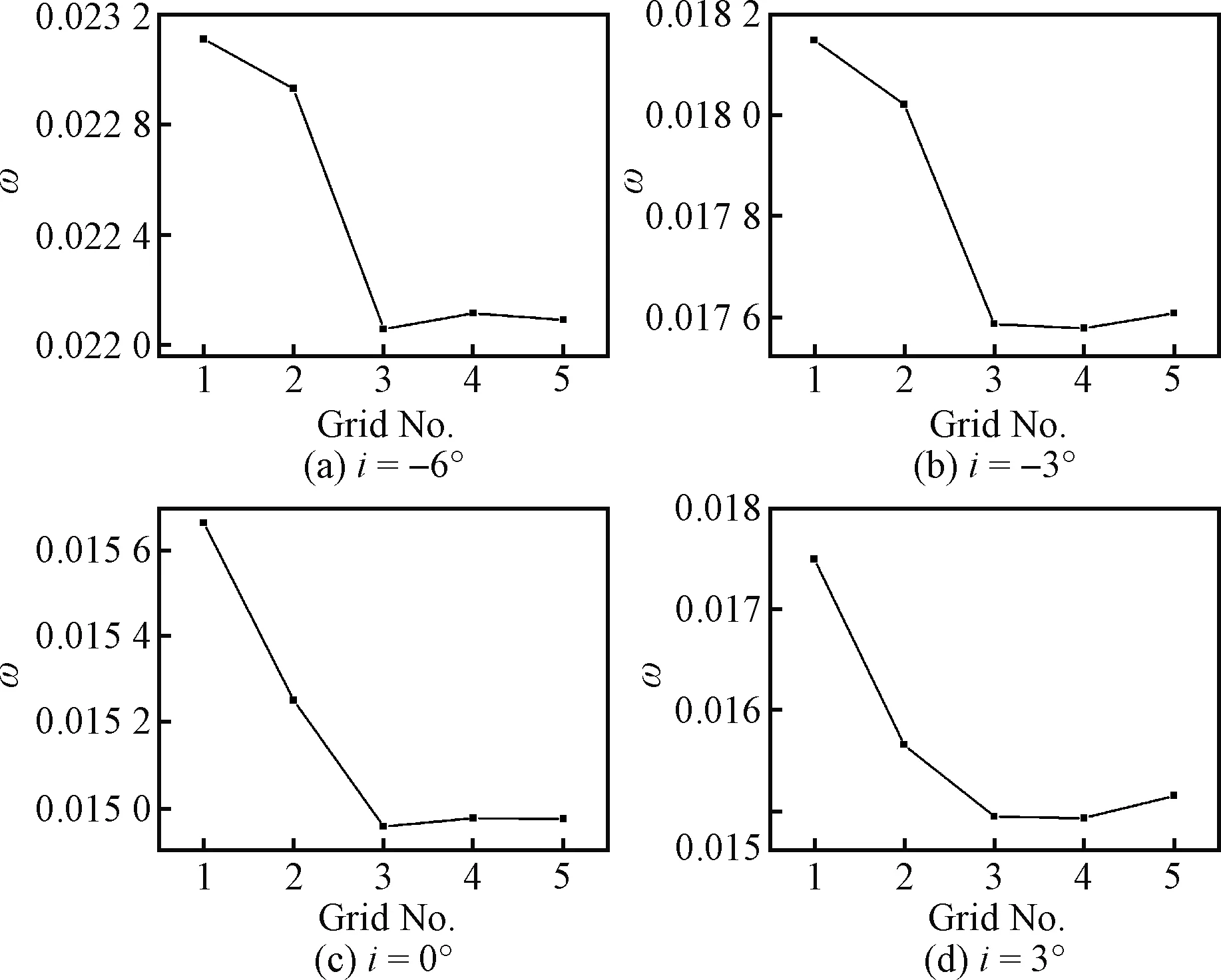
图5 不同网格下的总压损失系数-攻角特性对比

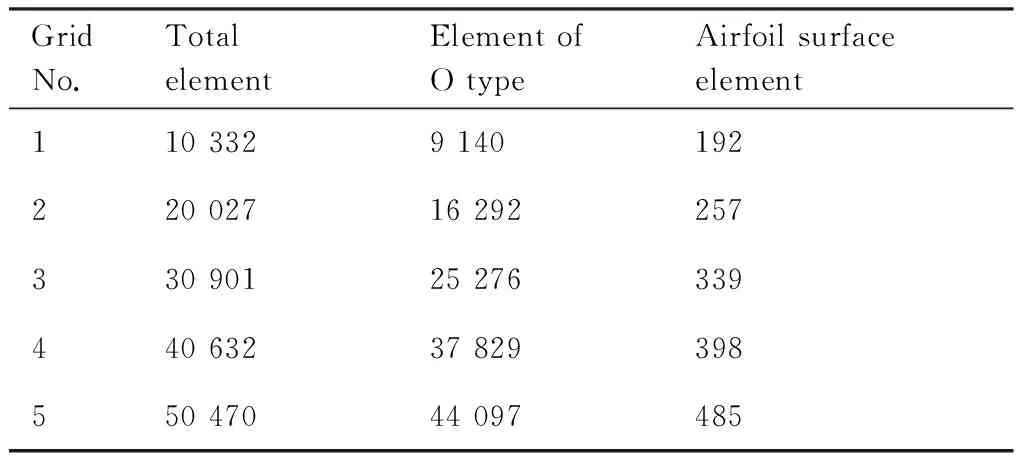
表2 不同规模网格参数

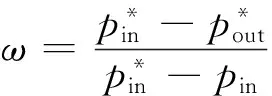
(7)

式中:p*和p分别表示总压和静压;下标“in”和“out”分别表示进口和出口。

根据图5中对比结果，本文选择Gird 4进行计算,既能保证网格无关性，又能尽量减少计算规模。

3 计算结果

3.1 前缘造型对叶型气动性能的影响

用上述数值方法对基准叶型和再设计叶型进行数值模拟计算，得到叶型的损失-攻角特性曲线如图6所示。5种设计叶型均能不同程度地降低叶型远离设计点工况时的总压损失水平，从而扩大叶型可用攻角范围。许用攻角定义为设计点(零攻角)下总压损失系数的2倍所对应的攻角范围。如图6中虚线所示，相对于基准叶型，K4、K4B、K7和K9叶型的许用攻角范围分别增加了1.46%、2.74%、6.09和7.30%。

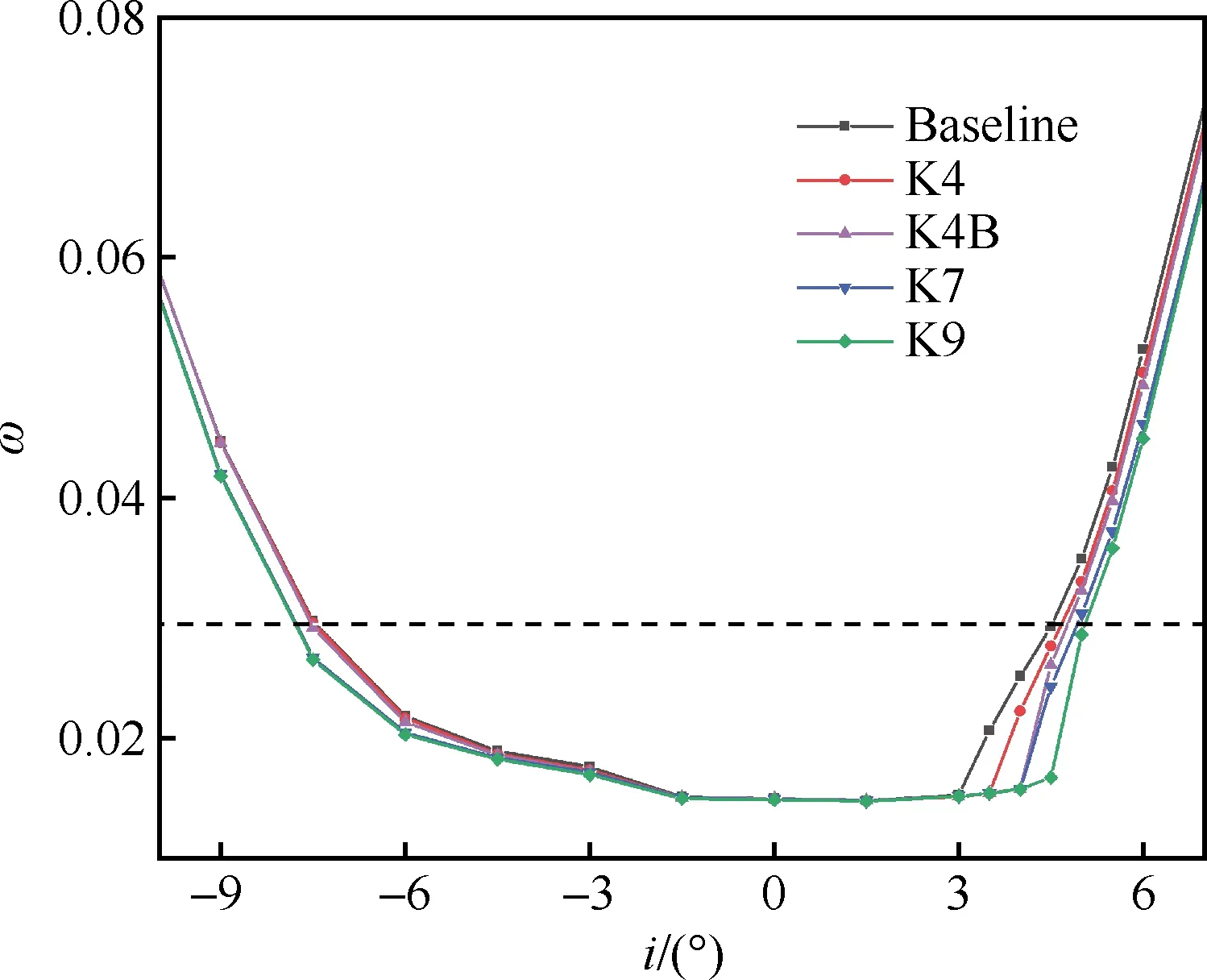
图6 基准叶型和再设计叶型的总压损失系数-攻角特性曲线

第1组K4、K7和K9的表现对比显示：随着叶型采用的前缘点曲率值增加，设计前缘的优化性能逐渐提升。在正攻角方向，特性曲线显示损失系数随攻角增大的变化过程中存在突变点，前缘几何形状的优化设计通过推迟该突变点的出现来扩大正攻角的工作范围。相比K4, K7和K9叶型在正攻角方向分别拓宽了0.26°和0.39°。在负攻角方向上，损失系数的增长较为平缓，K7和K9叶型在负攻角方向分别拓宽了0.29°和0.31°。

第2组Baseline、K4和K4B的对比显示：K4B相比K4，K4相比Baseline的性能各有所提升。K4B和K4前缘叶型在正攻角方向分别拓宽了0.15°和0.26°，但在负攻角方向变化很小，分别只拓宽了0.02°和0.07°。

根据文献[7]定义的尖峰扩散因子定量描述前缘吸力峰随来流攻角的变化，其表达式为

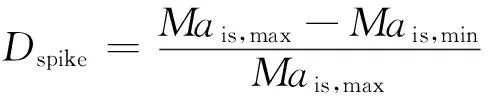
(8)

式中：Mais为等熵马赫数；“max”和“min”分别表示最大值和最小值。结果如图7所示。随着攻角增大，前缘滞止点位置向压力面移动，叶表流体需要绕过的前缘流程增加，加速过程变长，吸力峰强度变大。从图7可以看出，再设计叶型相对于基准叶型能有效推迟前缘尖峰攻角的出现，减小尖峰强度，降低流动扩散程度。定性地说，气动损失表现越好的叶型前缘，吸力峰开始出现时的攻角越大，在小攻角工况下Dspike数值越小，但其随攻角变化的增长速率也越大。注意到无论是在第1组还是在第2组中，气动表现更好的叶型因为增长率较大的原因，使其Dspike在大攻角下都完成了反超，这解释了其相对于基准叶型虽然损失突变点向后推迟，但总压损失在突变点后增长更快，当攻角继续增大时损失迅速增加到基本接近的水平。

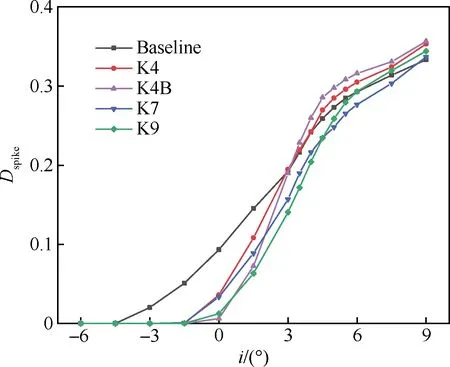
图7 基准叶型和再设计叶型的尖峰扩散因子-攻角特性曲线

Goodhand和Miller的研究[7]认为存在一个尖峰扩散因子的临界值，当Dspike低于该临界值时，叶型性能基本不受该前缘吸力峰的影响。根据图6中几种叶型在正攻角方向损失突变增大的位置判断，本文研究的叶型并不存在一个唯一确定的尖峰扩散因子临界值。式(7)定义的尖峰扩散因子只与吸力峰处的最大等熵马赫数和峰后谷底处最小等熵马赫数这2个数值相关，并不能完整刻画峰后边界层流速的变化模式，但是从下文的分析中，将会看到除了峰值大小外，峰后叶表静压的具体分布情况(边界层内流速变化模式)也与前缘分离泡的产生以及分离诱导转捩的出现息息相关，从而能够影响到叶型性能。

3.2 前缘造型对前缘流动的影响

为详细了解前缘形状对叶型气动性能的影响机理，分别选取一个正/负攻角(i=4°/-6°)典型工况分析边界层流动情况。i=4°时，Baseline总压损失最大，K4叶型次之，K4B、K7和K9叶型尚未超过突变点，总压损失水平基本相同。图8为各叶型在i=4°时叶表静压系数Cp分布，横坐标x/x0为归一化轴向弦长位置。从吸力面前缘处放大图可以明显看到吸力峰的存在，从前缘压力面上的滞止点开始到吸力峰位置处为气流的加速阶段。吸力峰之后，在逆压梯度作用下，流速开始下降，在图8中表现为吸力峰后曲线的陡降。除K9叶型前缘外，在陡然下降后曲线进入一个“平台”段，该段平缓的静压发展代表分离泡的出现：经过加速的气流在强逆压梯度的作用下发生分离，分离的气体在主流区高速气流的压迫下，在下游壁面再附，形成分离泡。

图9展示了各叶型在i=4°工况下前缘附近的流动情况。第1组K4、K7和K9的流线图对比显示：该分离泡的位置移向下游，分离泡变薄，但占据更宽的叶表范围。对应地，图8中3种叶型吸力面前缘静压系数“平台”段位置依次后移，数值变小，但长度增加。K9叶表静压系数在吸力峰后没有出现“平台”段，下降光顺连续，因此在图9(e)中也没有观察到分离泡的存在。另外，注意到约30%轴向弦长处K7与K9叶型亦出现了静压“平台”段，这表明在该处也有流动分离现象存在。第2组3种叶型前缘处均存在分离泡，且从Baseline到K4再到K4B，分离泡位置逐渐向下游移动，变薄变宽，与图8中3种叶型吸力面前缘静压系数“平台”段的特征相对应。约30%轴向弦长处K4B叶型出现了静压“平台”段，也表明其出现了二次流动分离。值得注意的是：K4B的吸力峰值相比Baseline和K4有所增加，但其实际气动表现却更好，这说明了对吸力峰影响的判断不仅要考虑峰值大小，更应考虑峰值后吸力面压力下降的具体变化情况。

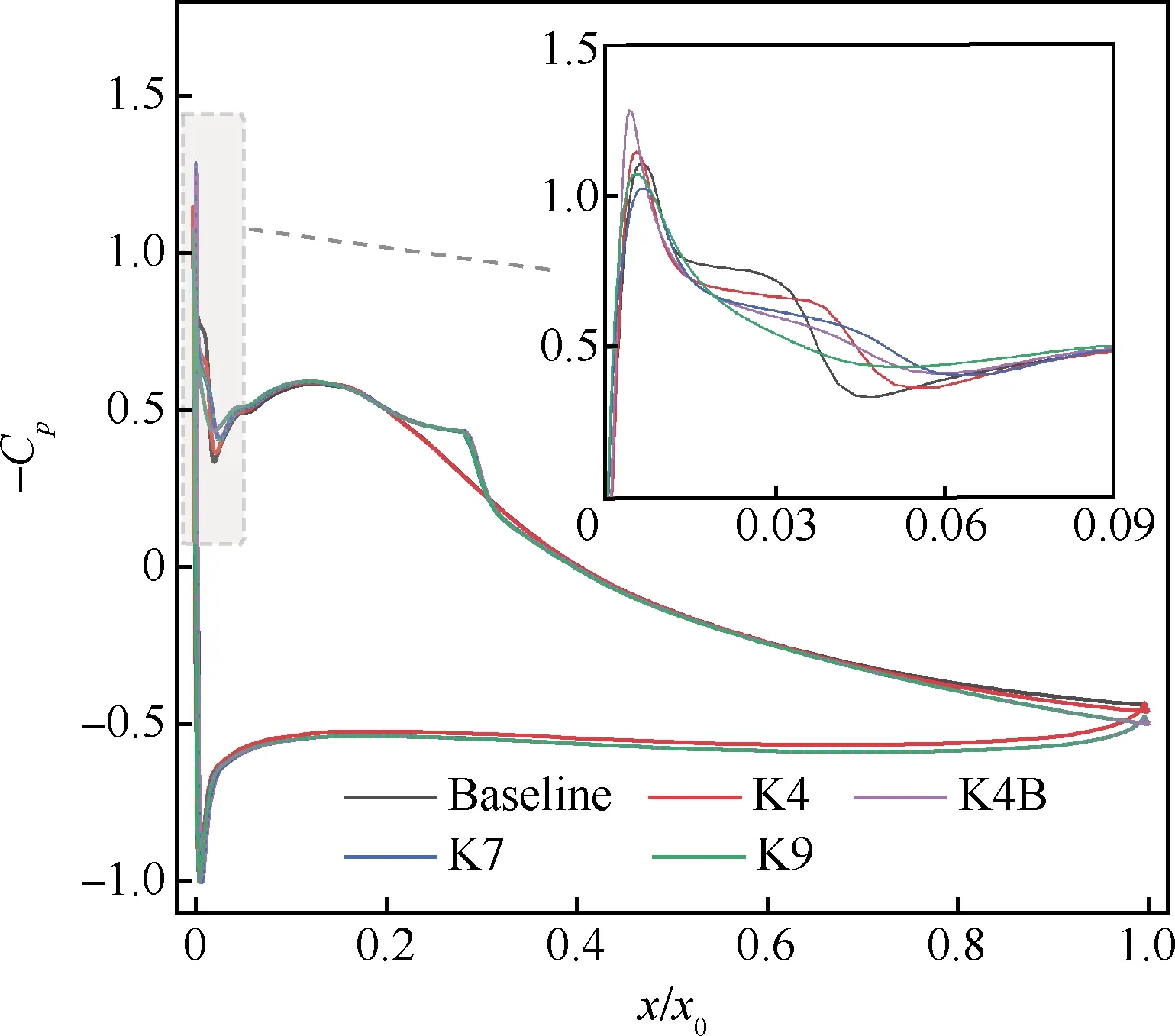
图8 i=4°时叶表压力系数分布

i=-6°时，图10的叶表静压系数分布显示各叶型流动损失差别相比i=4°时更小。此时前缘尖峰位于压力面上，逆压梯度下各叶型压力面前缘均出现了“平台”段，相应地图11所示压力面流线也表明了分离泡的存在。Baseline、K4与K4B的分离泡大小基本相同，K7与K9的相对更小。各分离泡的流向位置、厚度与长度和静压系数曲线“平台”段的特征基本对应。

图10 i=-6.0°时叶表压力系数分布

图11 i=-6.0°时前缘流线与压力云图

3.3 前缘造型对边界层发展的影响

为进一步分析前缘造型不同带来的前缘流动差异对叶型整体性能的影响，图12和图13分别给出了各叶型在i=4°时吸力面边界层位移厚度δ*和形状因子H的发展过程，横坐标s/s0为归一化的距前缘点吸力面弧长。可以看到Baseline、K4、K4B和K7叶型边界层位移厚度在前缘处有明显凸起，代表前缘分离泡引起的边界层增厚，K4B、K7和K9叶型在接近40%吸力面弧长位置处的凸起则代表了叶背中处的流动分离现象。图14和图15分别给出了边界层湍流间歇因子(γ)和湍动能(TKE)的分布情况，其中h为离壁面距离。可以判断：Baseline和K4叶型前缘分离后转捩为湍流再附，导致边界层迅速增厚，边界层内损失耗散增加，同时使得尾缘处出现了较大的边界层分离。K4叶型相比Baseline前缘分离泡位置更靠后，转捩到湍流过程中损失更小，因此造成的边界层增厚相对更慢。K4B和K7叶型前缘虽然也发生了流动分离，但其分离泡(图9(c)和图9(d))位置靠后，薄而细长，从图14(c)和图14(d)中可以看出该处流动分离没有引起转捩，因此分离流体以层流状态再附；K4B、K7与K9叶型边界层的转捩发生于30%～40%吸力面弧长位置，转捩位置的推迟使得其边界层增厚速度更慢。

图12 i = 4°时吸力面边界层位移厚度发展过程

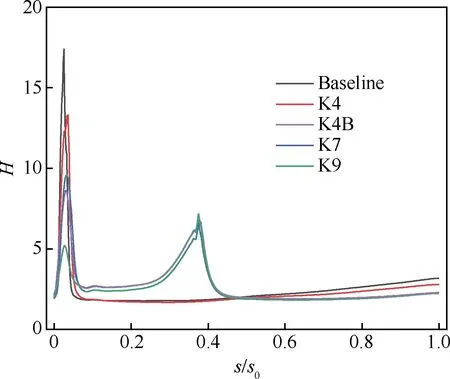
图13 i=4°时吸力面边界层形状因子发展过程

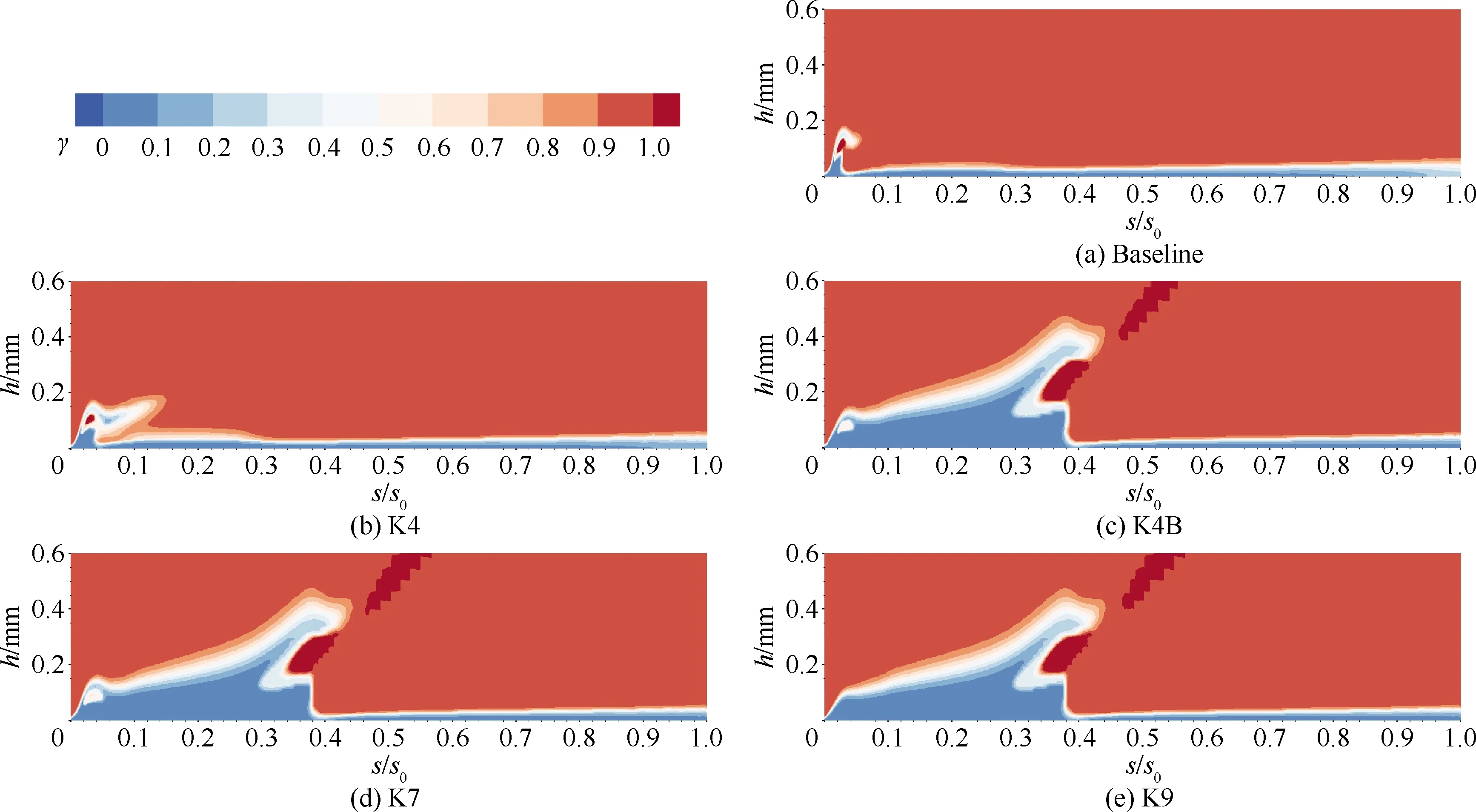
图14 各叶型在i=4°时吸力面边界层的湍流间歇因子分布云图

图15 各叶型在i=4°时吸力面边界层的湍动能分布云图

参考文献[24]中的方法提取边界层内损失分布：

(9)

(10)

其中:ρ为密度;δ为边界层厚度;v为速度。

由图16吸力面边界层损失分布可以看出Baseline和K4叶型边界层损失在前缘分离泡处迅速增大，而K4B、K7与K9叶型吸力面边界层起始层流段的损失发展非常缓慢，直到约40%弧长处在短暂的转捩过程后损失迅速增加。因为前40%弧长层流段的存在，其湍流边界层发展到尾缘处时的损失也远小于前2种叶型。

图16 i=4°时吸力面边界层损失分布

各叶型在i=-6°时压力面边界层位移厚度δ*和形状因子H的发展过程如图17、图18所示。可以看到5种叶型边界层位移厚度在前缘处均有明显凸起，形状因子也只存在前缘处一个尖峰。在i=-6°工况下各叶型压力面前缘处发生流动分离和湍流转捩后，边界层内流体一直保持湍流状态直到尾缘处分离产生尾涡。各叶型流动状态相似，区别主要在于前缘分离泡的位置和大小，以及由此造成的转捩过程的差异。

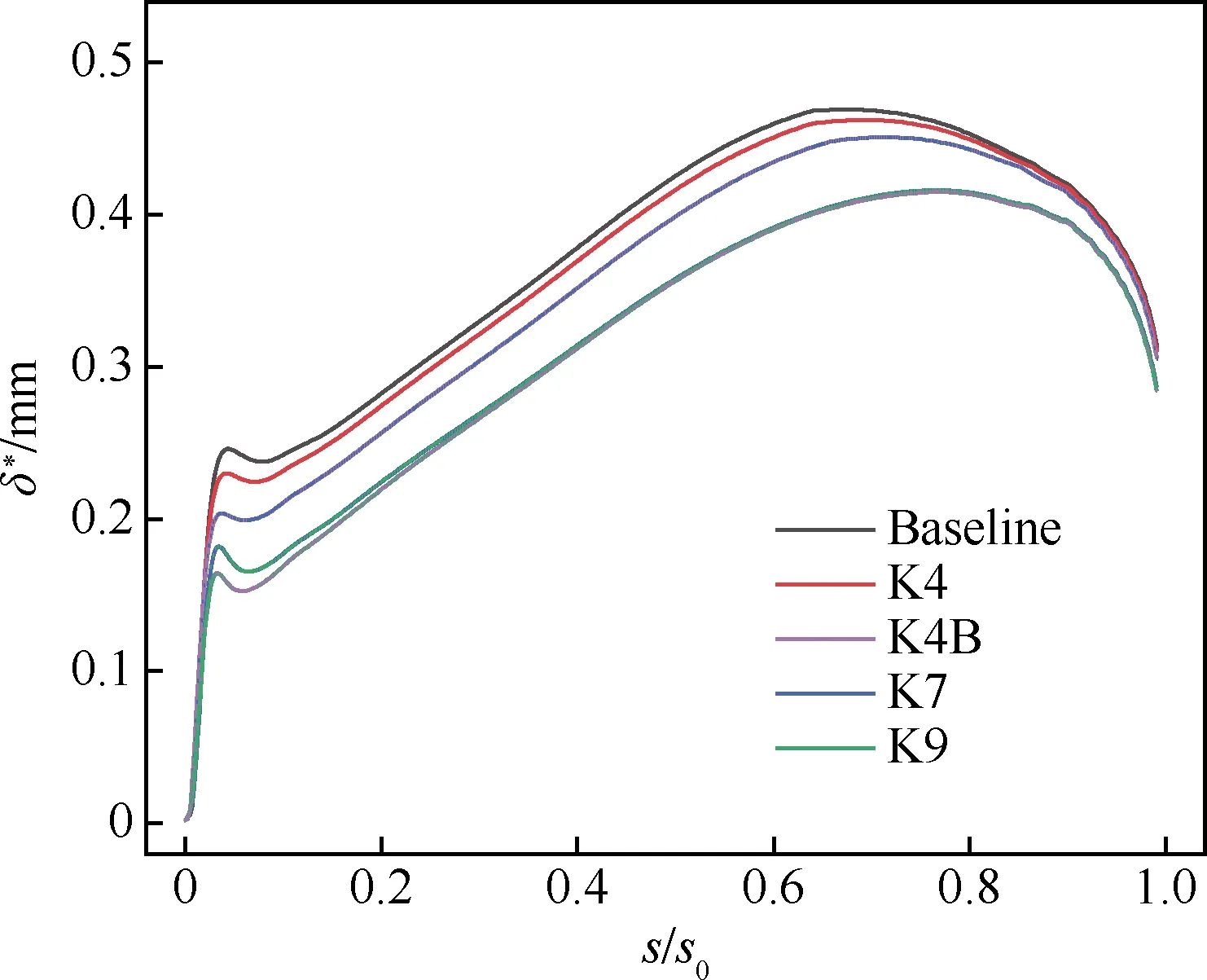
图17 i=-6°时压力面边界层位移厚度发展过程

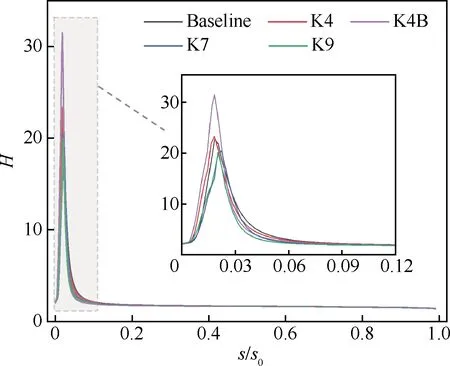
图18 i=-6°时压力面边界层形状因子发展过程

4 分析与讨论

第3节描述的前缘造型对流动的影响情况说明，前缘曲率对叶型性能的影响机理是通过调整叶表的静压分布，改变前缘吸力峰的强度和位置，影响边界层起始阶段的流动形态。当前缘附近压力分布比较平缓，吸力峰强度较小时，前缘流动能在非设计工况下保持层流状态，或是在分离泡后以层流再附，则能使压力损失保持在较小水平；若吸力峰强度增大，逆压梯度增加，则会会导致流动分离和分离诱导转捩现象的出现。而边界层的发展对起始状态的改变非常敏感，由此造成全弦长范围边界层内损失的改变从而对叶型的气动性能造成影响。

通过考察前缘流动需要满足的物理规律定性分析前缘曲率对前缘流场发展模式的影响。从定常不可压缩Navier-Stokes方程出发推导考虑物面曲率的边界层方程，可以得到如下结果[19]：

(11)

(12)

式(11)和式(12)建立在叶片表面坐标系上，其中ξ和η分别为曲面切线方向和法线方向坐标；uτ和un分别为边界层内的切向速度和外法向速度；ν为运动黏度。式(11)和式(12)中右端含K的项为考虑物面曲率对经典平面不可压缩层流边界层方程的修正。式(12)中右端项为流体绕流曲线物面需要提供的法向向心力。对式(12)稍作变形，在边界层内对压力做法向积分得到壁面与主流的压差为

(13)

根据数值仿真得到的边界层数据按式(13)计算i=4°工况下吸力面壁面与主流压差如图19所示。对i=4°工况下的Baseline叶型椭圆形前缘，叶表气流从位于前缘压力面一侧的滞止点开始沿叶表加速，在其到达前缘与吸力面主型线衔接点之前，随着椭圆弧前缘曲率减小，需要的向心力在前缘点附近迅速增加后变化趋于平缓。在衔接点处叶表曲率因为存在突变，需用压差提供的向心力突然减小，导致叶表静压突然增大，这就是吸力峰出现的流动机理。对重新设计的K4、K4B、K7和K9叶型而言，曲率从几何前缘点开始向两侧平滑地减小。因此在从压力面前缘滞止点到几何前缘点的流程中，流速和曲率均迅速增大，这导致压差在到达几何前缘点前更加迅速的增长。如图19所示，第1组中各叶型前缘点曲率值越大，则其在前缘点处压差值和增长速率越大。第2组中，前缘点附近曲率值下降越慢，分布越饱满，则前缘点处压差值和增长速率也越大。

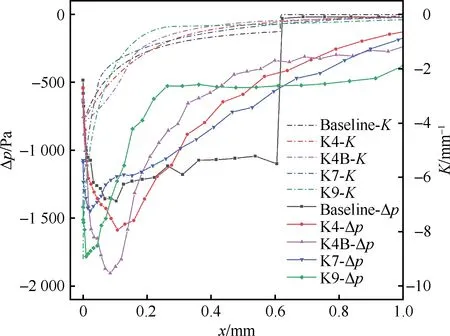
图19 i=4°时吸力面壁面与主流压差和对应位置曲率

当越过前缘点后，各叶型的曲率开始下降，部分抵消了流速增加带来的压差上升。第1组中K7和K9叶型相比K4叶型，前缘点曲率更大，曲率下降更快，因此这种抵消作用更加明显，压差由升转降的极值点也更加提前。K7相比K4压差的极值点有所下降，但K9叶型压差极值点却略有上升，这是由于气流在滞止点与几何前缘点之间过度加速所导致的。第2组中K4B相比K4，K4相比Baseline曲率值下降更慢，则其抵消流速增加带来压差上升的作用相对滞后，最后形成的压差由升转降的极值点也相对滞后，峰值变大。K4B叶型极值点压差甚至比K9还大，但位置靠后，因此其损失比K9更大，与K7相当。

需要注意的是，无论是单纯的增加前缘点的曲率，还是调整曲率分布增加前缘大曲率值的范围(在图像上使曲率分布在靠近前缘点处更为“饱满”)均会在几何上使得前缘更加尖锐。在满足连续性的条件下，这种更加尖锐的前缘因为会使压差峰值增大或出现位置滞后的缘故，优化效果可能收效甚微，甚至还会出现一定程度的恶化。这就是之前一些学者认为前缘大曲率会缩小许用攻角范围[3,6]，而另一些学者却发现更尖锐的前缘有时能扩大攻角范围[2,7]的矛盾现象产生的原因。

根据上述曲率对前缘流动的影响机理，可以提出以下叶型前缘曲率设计的原则：

1)保持曲率的连续性，特别是前缘与主型线衔接点处的曲率连续。在使用传统圆弧形或椭圆形前缘时可以考虑用高次多项式实现平滑衔接以防止曲率突变导致大强度吸力峰的出现。

2)调整曲率分布使在关心工况下，前缘气流加速段与曲率下降段重合，尽量减小压差的变化幅度，使其在达到峰值后迅速下降，将压差的大幅升降压缩在前缘点附近尽可能窄的范围内。

3)前缘点处曲率不能过大，这是加工精度的限制，也是优化原理的要求。通过CFD仿真可以确定在满足连续性条件下能使优化效果最佳的前缘曲率大小。

4)取决于是否偏向优化正/负方向攻角范围的需要，可以将前缘设计为非对称形状，减小气流从滞止点到几何前缘点间的加速效果。

5)为同时扩大正负攻角的许用范围，需要同时考虑到滞止点在吸力面和压力面侧时前缘起始的绕流情况。因此可以考虑在前缘曲率的设计上采用分段处理的方式，将本文提出的造型方法与传统的椭圆形方法、多项式造型等结合使用。

5 结 论

本文提出了一种基于给定曲率分布的前缘造型方法，通过该方法可以实现对前缘曲率的精确控制。将该造型方法应用于某工业级压气机的CDA叶型上，通过数值仿真验证了该造型方法的有效性，研究了前缘曲率大小和曲率分布对前缘流动和叶型损失的影响规律与物理机理，提出了优化前缘几何形状的建议。主要结论如下：

1)本文提出的造型方法从给定曲率分布出发，在满足坐标位置、斜率和曲率连续性的条件下构造出造型曲线。该方法自由度高，普适性好，能和其他造型方法结合使用。因为可以实现对曲率分布的直接控制，所以结合前缘曲率对叶型性能的影响规律，可以方便快捷地实现对叶型前缘的优化设计。

2)再设计叶型相比基准叶型能有效拓宽许用攻角范围，降低尖峰扩散因子，抑制甚至消除前缘分离泡，避免边界层提前转捩的发生，减小边界层厚度和流动损失水平，从而达到优化效果。在所研究的几种叶型中，前缘点曲率越大，并且靠近前缘点处曲率分布越饱满，则优化效果越好。

3)分析考虑物面曲率的简化边界层方程发现，曲率对流动的影响是通过边界层法向压力和曲率的关系，调整壁面静压分布，影响吸力峰强度实现的。再设计叶型的曲率分布更有利于减小叶表压差，削弱吸力峰。

4)根据曲率对前缘流动的影响机理，设计前缘几何形状时需要确保曲率的连续性，设计合适的曲率分布以减小前缘吸力峰的强度。根据具体的设计需求，可以灵活使用本文提出的造型方法设计压力面/吸力面非对称的前缘或与其他传统前缘结合使用。