异常值和未知观测噪声鲁棒的非线性滤波器

方安然，李旦,3,*，张建秋

1.复旦大学 智慧网络系统研究中心，上海 200433 2.复旦大学 电子工程系，上海 200433 3.上海市空间智能控制技术重点实验室，上海 201101

在雷达、声呐、通信和语音识别等应用中，观测中随机出现异常值是一种十分常见的现象[1-2]。例如，无线通信中，电路通断暂态过程产生的脉冲干扰；在雷达系统或声呐系统中，人为或自然因素产生的冲击性干扰，而引起雷达或声纳观测的随机异常波动[3]等。文献[4]表明：这种观测的随机异常波动是一种非高斯噪声，其概率密度分布有一个比高斯分布更厚重的“尾部”，因此通常称其为长尾分布。传统非线性系统的滤波方法一般聚焦于非线性过程的近似描述，如：扩展卡尔曼滤波(Extended Kalman Filter, EKF)[5]，就是利用一阶泰勒展开对非线性方程近似线性化，然而，由于它的线性化误差较大，因此就造成滤波性能不佳；迭代扩展卡尔曼滤波(Iterated Extended Kalman Filter, IEKF)[6]对EKF的改进，就是通过迭代的逐步逼近，以减小线性化误差，却也因此造成了运算复杂度的上升；利用Sigma点方法逼近非线性过程，在避免迭代计算的同时降低了状态估计误差，这一类算法包括利用无迹变换(Unscented Transform, UT)的无迹卡尔曼滤波(Unscented Kalman Filter, UKF)[7]、利用球面容积积分的容积卡尔曼滤波(Cubature Kalman Filter, CKF)[8]和利用高斯-埃尔米特积分的正交卡尔曼滤波(Quadrature Kalman Filter, QKF)[9]等。但是，以上非线性滤波方法，都是假设观测噪声为高斯白噪声。因此在含异常值的噪声环境中，即存在随机观测异常值或非高斯的噪声环境中，这些算法的性能都会显著下降，甚至失效[5]。

针对非高斯非线性系统的滤波，传统算法主要有以高斯混合模型(Gaussian Mixture Model, GMM)来逼近非高斯分布的高斯和滤波(Gaussian Sum Filter, GSF)[10]，以及利用蒙特卡洛模拟近似描述非高斯分布的粒子滤波(Particle Filter, PF)[11]等两种。尽管这两种算法都能处理含异常值或非高斯噪声环境中的动态滤波问题，但它们都需要有非高斯噪声的准确先验知识，以及都存在运算复杂度偏高等问题[5]。为了解决这些问题，文献[2]提出了对异常值(离群点)鲁棒的卡尔曼滤波(Outlier-Robust Kalman Filter, ORKF)。它通过对卡尔曼滤波算法进行修正，以满足非高斯非线性系统滤波的要求。不过由于其对先验噪声协方差准确与否十分敏感，因此鲁棒性欠佳且应用受限。为了进一步提高滤波算法的鲁棒性，文献[12]以Kullback-Leibler散度(Kullback-Leibler Divergence, KLD)为目标函数，对非线性观测方程进行线性化，提出了一种后验线性化滤波(Posterior Linearization Filtering, PLF)算法。尽管该算法对噪声先验信息的准确与否并不敏感，但其估计性能欠佳。针对这一问题，文献[13]提出了最大相关熵的无迹卡尔曼滤波器(Maximum Correntropy Unscented Kalman Filter, MCUKF)，改善了状态估计的性能，不过其收敛较慢，且高度依赖滤波参数的选择是否合适。不幸的是：如何选择滤波参数，目前还没有令人信服的解决办法[14]。为此，以Huber函数[15]作为损失函数，文献[14]又提出了鲁棒微分无迹卡尔曼滤波器(Robust Derivative Unscented Kalman Filter，RDUKF)，这是因为基于Huber函数的滤波参数选择，目前已有较成熟的方法[14]。然而，RDUKF要求动态系统的状态转移方程为线性，因此不能应用于非线性系统的滤波。文献[16-18]则报道了基于Huber函数的另一类滤波算法，称为基于Huber的无迹滤波器(Huber-based Unscented Filter，HUF)，尽管它们适用于非线性系统的滤波，但必须有观测噪声二阶统计量的先验。为了克服这一缺点，文献[19]报道了一种R-自适应无迹卡尔曼滤波器(R-Adaptive Kalman Filter, RUKF)，不幸的是，该方法一旦受到异常值的干扰，则极易发散[20]。

针对含异常观测值非线性系统的滤波，本文提出了一种新的滤波算法，称之为对异常值鲁棒的后验线性化滤波器(Outlier-Robust Posterior Linearization Filter, ORPLF)。分析表明：以Huber损失函数代替最大后验(Maximum a Posterior, MAP)准则中加权观测误差的l2范数，就得到了一个新的最优化准则函数。由于Huber损失函数同时具有l1和l2范数的性质，因此借助于这个新的最优化准则函数，本文推导的滤波器就兼具了l1范数对异常值的鲁棒性，以及l2范数对函数拟合的精确性。当观测噪声的分布未知时，则可通过箱线图法[21]估计其分布的方差，这样就进一步提出了对异常值和未知观测噪声鲁棒的后验线性化滤波器(outliers and unknown Observation Noise-Robust Posterior Linearization Filter, ONRPLF)。仿真实验验证了分析结果的有效性，它们也表明：本文算法的滤波性能(包括误差和鲁棒性)在含异常值的(未知)观测噪声中优于现有文献报道的非线性滤波类算法。

本文内容组织如下：第1节回顾了PLF算法，并给出了利用Huber损失函数的MAP准则，进而利用该准则推导了适用于非线性系统的ORPLF算法；第2节给出了Huber函数中调谐参数μ的确定方法，也给出了利用箱线图法估计噪声分布方差的方法；第3节给出了目标跟踪的仿真实验；第4节总结了全文。

1 异常值鲁棒的非线性滤波器

1.1 后验线性化滤波器

假设一离散非线性系统的状态空间模型为[20]

xk=fk-1(xk-1)+wk-1

(1)

yk=hk(xk)+vk

(2)

(3)

式中：Ak∈Rd×n为线性化的观测矩阵；bk∈Rd为线性化的偏差；ek∈Rd和ek～N(ek|0,Ωk)表示线性化时的误差；Ωk为线性化误差ek的协方差；Ak、bk、Ωk为在时刻k对hk(xk)线性化的参数。

文献[12]给出了一种通过最小化KLD来进行非线性观测方程线性化的方法，其KLD定义为

(4)

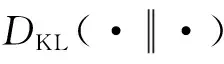
由文献[22]知，KLD反映的是两个分布的匹配程度。匹配程度越高，KLD就越小。若两个分布完全匹配，则它们之间的KLD就为0。据此，数学上最小化KLD就可表示为[12]

p(xk|yk,Ak,bk,Ωk))

(5)

当状态xk的分布p(xk)和非线性方程hk(·)都已知时，利用hk(·)关于p(xk)的统计线性回归(Statistical Linear Regression, SLR)，可得到式(5)的解为[12]

(6)

(7)

(8)

(9)

(10)

(11)

式(9)～式(11)中的积分可以通过不同的数值方法进行逼近[5]，例如：无迹变换[7]、球面容积积分[8]、高斯-埃尔米特积分[9]等。这样，近似线性化后的新观测方程就为

yk=Akxk+bk+rk

(12)

式中：rk=ek+vk为一个含异常值的观测噪声。

由于ek与vk是相互独立的，而vk去除异常值之后的协方差为Rk且ek～N(ek|0,Ωk)，因此rk去除异常值之后的协方差就为(Ωk+Rk)。这样，将含异常值的非线性观测方程，变换成了含异常值的线性观测方程。若采用广义高斯滤波[5]的方法进行状态预测，那么据线性化之后的观测方程(12)，执行卡尔曼滤波的更新步骤[5]，就可得到文献[12]的PLF算法。

1.2 异常值鲁棒的后验线性化滤波器

从最大后验(Maximum a Posterior, MAP)的角度，在高斯噪声环境中PLF算法的状态更新就是最大化如下函数[12]

(13)

对式(13)取负对数，则MAP就等价于最小化如下损失函数：

(14)

从式(14)中，可以发现它采用的是l2范数。由文献[15]知，l2范数的预测值距离真实值越远，则其惩罚力度越大，这就意味着它对异常值比较敏感。也就是说，l2范数容易受到随机异常值的干扰，甚至有可能会导致算法失效。因此，l2范数不适用于含有随机异常观测值系统的滤波。由文献[15]知，l1范数相较于l2范数对异常值具有更高的鲁棒性。可是，l1范数可能存在不可导的奇异点，这为最小化l1范数的计算带来了困难。为此，本文期望通过引入Huber损失函数，在降低异常值对滤波干扰的同时，又可保证等效l1范数处处可导。

Huber损失函数的定义为[15]

(15)

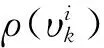
(16)

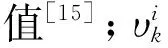
υk=(Ωk+Rk)-1/2[yk-(Akxk+bk)]

(17)

式中：A1/2为对称正定矩阵A的Cholesky分解；AT/2为A1/2的转置，满足A=A1/2AT/2,A-1/2是A1/2的逆矩阵，A-T/2是AT/2的逆矩阵。

利用式(15)的Huber损失函数，将式(14)改写为

(18)

对式(18)中的xk求导并令该导数等于零，有

(19)

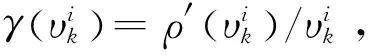
(20)

定义矩阵：

(21)

那么由式(17)，有

(22)

将式(20)～式(22)代入式(19)，并利用文献[15,18]中的矩阵恒等式，有

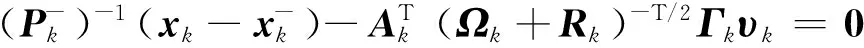
(23)

再将式(17)代入式(23)，可得

Γk(Ωk+Rk)-1/2[yk-(Akxk+bk)]=0

(24)

(25)

整理得

(26)

利用如下矩阵求逆公式[23]：

(A-1+BC-1D)-1=A-AB(DAB+C)-1DA

(27)

有

(28)

将式(28)代入式(26)，得

(29)

整理得

(30)

再用一次矩阵和求逆公式，有

(31)

将式(31)代入式(30)，有

(32)

(33)

其后验分布协方差为

(34)

将式(33)代入式(34)，整理得

(35)

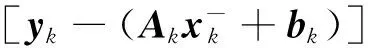
(36)

又因为：

(37)

(38)

将式(37)和式(38)代入式(36)，有

(39)

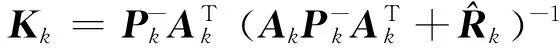
(40)

式(33)和式(40)就是引入Huber损失函数之后，本文重新推导的PLF的更新步骤。也就是说，得到了对异常值鲁棒的后验线性化滤波器(Outlier-Robust Posterior Linearization Filter, ORPLF)。

下面给出ORPLF算法的步骤：

算法1ORPLF算法

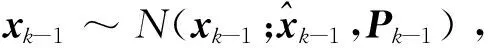
步骤1预测步骤：与传统的广义高斯滤波[23]算法完全相同：

(41)

(42)

式(41)和式(42)中的积分可采用无迹变换(Unscented Transform, UT)[7]、球面容积积分[8]、高斯-埃尔米特积分[9]等进行近似计算。

步骤2更新步骤：

1)观测方程线性化：依式(6)～式(12)，将观测方程hk(xk)线性化。

2)计算尺度函数：依式(17)，式(20)和式(21)，计算对角矩阵Γk。

3)状态更新：

(43)

(44)

2 Huber函数的相关参数估计

2.1 Huber函数调谐参数μ的确定方法

式(15)和式(16)表明：Huber损失函数是一个分段函数，调谐参数μ为阈值，用于判断观测是否属于异常值。若观测不是异常值，那么Huber函数就是l2范数，最小化式(18)就等价于MAP。若观测是异常值，那么Huber函数就是l1范数。在算法中的直观表现就是依据真实值与预测值之间的归一化残差υk，动态地调整系统模型中的观测协方差：归一化残差越大，相应的观测协方差就越大，反之亦然。

判断观测是否属于异常值，一方面取决于观测的真实值与预测值之间的归一化残差向量υk，另一方面取决于调谐参数μ的取值。据式(17)知：归一化残差向量υk与线性化后修正的观测方差(Ωk+Rk)有关。由于线性化误差Ωk通常很小[12]，因此主要取决于Rk。也就是说，观测yk是否属于异常值同时也取决于观测方差Rk的取值。而在Huber函数中，调谐参数μ是判断观测是否属于异常值的阈值，残差的绝对值超过此阈值时，就判定为异常值，低于此阈值则判定为非异常值。

若随机观测噪声服从高斯分布，那么，据3σ原则：在高斯分布中，数值分布在(m-3σ,m+3σ)中的概率约为99.74%，其中m是分布均值，σ是分布方差。因此，对于高斯分布，若将调谐参数μ取为3倍方差，就能很好地判断υk是否属于异常值。由于υk是经过归一化的残差，方差为1，因此可取μ=3。

若随机观测噪声属于非高斯分布，据文献[24]，理论上，Huber函数的调谐参数μ的最优值μ*与分布中的异常值概率ε*(0<ε*<1)之间存在如下函数关系：

(45)

式中：当ε*→0时，μ*→∞，此时Huber函数就完全是l2范数；当ε*→1时，μ*→0，此时Huber就完全是l1范数。在Huber函数中，调谐参数μ的取值影响异常值的判定，直观上来说，调谐参数μ越小，就会有越多的样本被判定为异常值，反之亦然。因此，Huber函数的调谐参数μ应当与噪声中异常值的占比相匹配。若调谐参数μ取值过大，就会导致一些异常值被判定为非异常值。这样再据l2范数进行优化时，会导致较大的状态估计误差，造成算法鲁棒性不佳；若调谐参数μ取值过小，则会导致一些非异常值被判定为异常值，若对其进行l1范数优化，就失去了l2范数的低误差拟合性，而造成算法性能下降。

在式(45)中，μ*不可显式求解。为了近似求解μ*，定义函数g(μ*)：

(46)

对式(46)求导，得

(47)

因此，可知函数g(μ*)是单调减函数。

在式(46)中，注意到，当μ*=3时，ε*≈2.547×10-4。考虑到函数的单调性，若ε*≤2.547×10-4，可近似地认为，理论上调谐参数的最优值μ*≥3。因此，在实际应用中，在近似认为随机观测噪声服从高斯分布的场合，可将调谐参数确定为μ=3。而当ε*∈(2.547×10-4,1)时，由于μ*→0时g(μ*)→∞，且μ*=3时g(μ*)≈1.003-1/(1-ε*)<1.003-1/(1-2.547×10-4)≈0，因此可以采用二分法近似求解调谐参数的最优值μ*，并将此最优值确定为Huber函数中的调谐参数μ。

在实际应用中，若随机观测噪声中的异常值概率未知，那么可以根据文献[14]推荐的调谐参数典型值，确定Huber函数的调谐参数μ=1.345。

2.2 箱线图法确定噪声分布参数

1.2节的ORPLF算法，针对的是观测噪声分布已知的非线性系统。若观测噪声分布未知，需要在此基础上再加上参数估计算法。采用箱线图法[21]检测异常值，并估计分布参数，就进一步得到了对异常值和未知观测噪声鲁棒的后验线性化滤波器(outlier and unknown Observation Noise-Robust Posterior Linearization Filter, ONRPLF)。

箱线图是一种显示一组数据分布情况的方法。在统计学中，将所有样本的数值从小到大排列，并分成四等分，其中处于3个分割点位置的数值就称为四分位数，按照数值从小到大的顺序，依次是下四分位数Q1、中位数Q2和上四分位数Q3，上四分位数与下四分位数的差值就称为四分位数差(Inter Quartile Range, IQR)。可利用箱线图来检测异常值[21]，即：大于上四分位数1.5倍四分位数差的值，以及小于下四分位数1.5倍四分位数差的值，都可划为异常值。由于四分位数受异常值影响较小，因此箱线图法具有较高的鲁棒性[21]。

利用箱线图法检测出异常值之后，将数据中的异常值除去，得到了经清洗后的数据，再对它们计算其统计特征，可得到滤波需要的统计分布参数。箱线图确定噪声分布参数的算法，可由以下计算步骤组成：

算法2箱线图法确定统计分布的参数

若一组数据{Di|i=1,2,…,ND}中存在异常值，执行以下步骤确定其去除异常值后统计分布的参数：

步骤1计算上四分位数Q3和下四分位数Q1。

步骤2计算四分位数差Riq=Q3-Q1。

步骤3检测异常值：若Q1-1.5Riq≤Di≤Q3+ 1.5Riq，则Di不是异常值；否则，Di是异常值。

步骤4计算分布参数：根据异常值占总样本数的比例确定异常值概率；将样本去除异常值之后，计算其分布参数，包括均值和协方差等。

由于箱线图法确定分布参数需要一组具有一定样本量的噪声数据，因此在确定噪声分布参数时，可对观测序列进行分块处理，这样就能得到一组样本。即对观测序列块k=jL-L+1:jL(j=1,2,…,L, 其中L是序列块的长度)，进行状态估计，然后采用箱线图法就可得到当前待求的未知参数，再进行下一个观测序列块的状态估计。

本文ONRPLF算法的步骤如下：

算法3ONRPLF算法

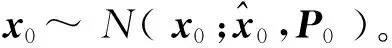
当j= 0, 1, …，执行以下操作：

步骤1对时刻k=jL+ 1：jL+L，执行算法1所示的ORPLF算法，得到状态xjL+1:xjL+L的分布。

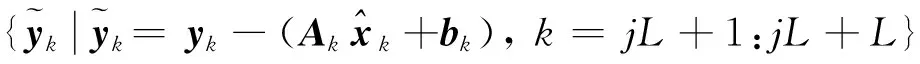
观测序列块的长度L，既会影响箱线图法推断方差的准确性，也会影响ONRPLF的收敛速度。根据文献[25]，对于一组采样，若要求方差推断的误差更低，应适当增加样本量。因此，若L过小，则方差推断的准确性就会降低，进而影响到滤波性能，从而使ONRPLF的误差增大。然而，由于ONRPLF必须等全部采集完下一个观测序列块数据后才能批处理进行估计，因此，若L过大，将使ONRPLF的收敛速度下降，且影响算法的实时性。因此，在实际应用中，应根据实际情况和需求合理选择观测序列块的长度L。

根据文献[25]，方差推断所需的样本容量L-与事先给定的置信水平1-α，及估计方差偏离置信区间中点的相对误差ξ之间存在如下关系：

(48)

式中：Z1-α/2表示标准正态分布分位数值。

若取置信水平1-α=95%，相对误差ξ=0.2，则由式(48)可得L-≈42.4。考虑到箱线图法在方差推断之前已经剔除了异常值，因此在确定样本量时应当留有一定的余量，即观测序列块的长度L应当大于L-。又因为过大的L将造成收敛速度和实时性的下降，因此在本文的仿真实验中，将观测序列块的长度取为L=50。

此外，由于Huber函数的调谐参数μ是依据异常值出现的概率εk确定的，而εk的精确度又受限于参数估计的样本数，即观测序列块的长度L，因此求μ近似解的精度也不宜定得过高。考虑到L=50，因此εk的精度是±0.02，在本文中，可将二分法求近似解的精度定为±0.02。

3 仿真实验

本节将进行仿真实验，以验证本文提出的ORPLF和ONRPLF算法的有效性和鲁棒性。针对一种机动目标追踪(Maneuvering Target Tracking, MTT)[12]问题，提出两种算法与PF、ORKF、PLF、MCUKF和HUF算法的性能进行比较。这是因为PF是非线性滤波问题的经典算法[5]；文献[20]的研究表明：ORKF算法是目前若干种对异常值鲁棒滤波算法中性能最好的算法；文献[13]表明：MCUKF算法是目前对长尾噪声最鲁棒的算法；而HUF则是Huber类型滤波中的经典算法[17]。

该MTT模型的状态转移方程为

xk+1=F(Δk)xk+wk

(49)

式中：

F(Δk)=

(50)

式中：τ=0.2 s为采样间隔；wk∈Rn为随机状态转移噪声，服从零均值协方差为Qk的高斯分布：

(51)

式中：q1和q2为运动模型的参数，q1=0.5 m2/s3，q2=10-6rad2/s3。

MTT模型的观测方程为

(52)

式中：arctan2(·,·)为四象限反正切函数；h=50 m是目标的高度；vk为一种含异常值的随机观测噪声，服从长尾分布，可用如下多维高斯混合分布来描述[12]：

p(vk)=(1-ε)N(vk|0,Σ1)+εN(vk|0,Σ2)

(53)

式中：ε为一个参数，表示异常值出现的概率；Σ1=diag([1 000,(3π/180)2,(30π/180)2, 1])是背景高斯噪声的协方差；Σ2=diag([1 000,(30π/180)2,(30π/180)2, 100])是异常值的协方差。

在仿真实验中，本文算法ORPLF和ONRPLF中的积分均采用UT变换进行逼近，UT变换中的参数与文献[7]中的相同。ONRPLF算法中L=50。更新Huber函数的调谐参数μ时二分法求近似解的精确度为±0.02。PF中采样粒子数为5 000。ORKF、PLF、MCUKF和HUF中的参数分别采用文献[20]、文献[12]、文献[13]和文献[17]中性能最佳的参数。

本文将采用目标位置坐标的均方根误差(Root Mean Square Error, RMSE)作为评价指标，来量化各种滤波器的性能。为获取RMSE，每组实验进行100次蒙特卡洛仿真。

3.1 不含异常值的仿真

首先来看不含异常值的情况，即异常值出现的概率ε= 0。此时，对每一种算法，给定观测噪声的协方差为R0=Σ1=diag([1 000,(3π/180)2,(30π/180)2, 1])。由于UKF是一种广泛应用的非线性滤波器[7]，因此在仿真实验中又加上了这种滤波算法。由于观测噪声服从高斯分布，因此在本文算法ORPLF中，更新调谐参数μ时二分法求近似解的精确度为±0.02。Huber函数的调谐参数μ=3。ONRPLF算法中L=50，Huber函数的调谐参数赋初值μ=3。仿真结果如图1和表1所示。

在表1中，本文两种算法ORPLF与ONRPLF是平均RMSE最小的算法。在图1中，小图展示了RMSE范围在7～15 m之间的图形细节。可以发现：本文两种算法ORPLF和ONRPLF，以及算法MCUKF的RMSE最终都收敛到了与UKF相近的性能，其中本文算法收敛最快，MCUKF收敛最慢。此外，在图1中，ORKF和PLF算法收敛较快，但最终并没有收敛到与UKF相近的RMSE。PF和HUF的RMSE较大，其中HUF收敛更慢。在不含异常值的条件下，除去本文的两种算法，这些适用于非高斯环境的算法性能都不如UKF，这是因为它们都为了保证对异常值的鲁棒，因而牺牲了一部分高斯噪声下的性能。

图1 不含异常值的仿真

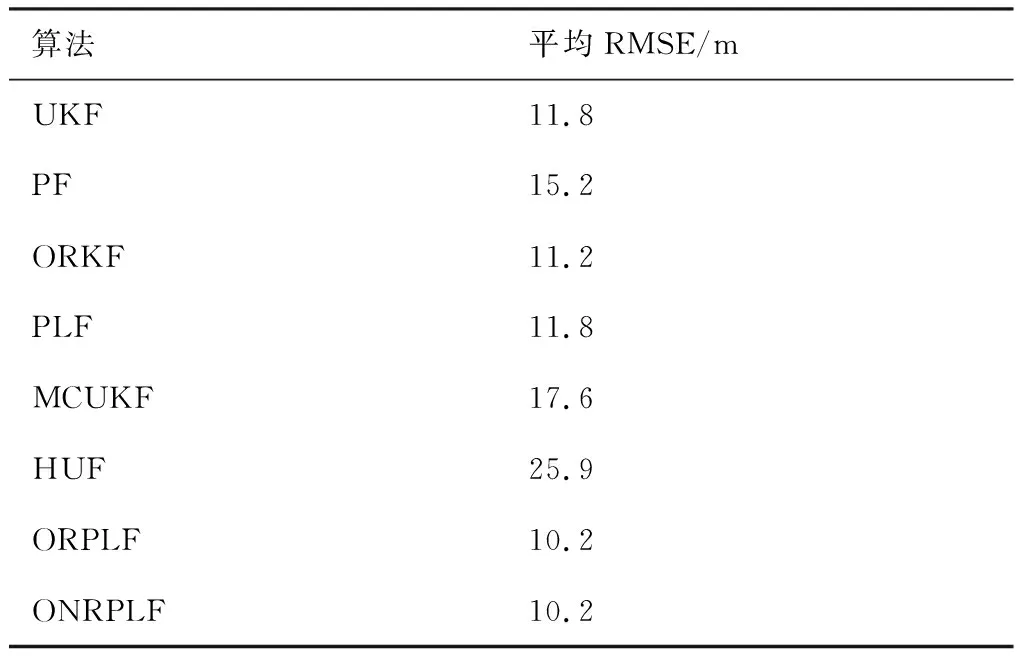
表1 不含异常值的平均RMSE

3.2 已知准确噪声协方差的仿真

接下来仿真观测含有异常值的情况，异常值出现的概率ε=0.4。对于算法RKF、PLF、MCUKF、HUF，及本文算法ORPLF和ONRPLF，仍给定观测噪声的协方差为R0=Σ1=diag([1 000,(3π/180)2,(30π/180)2, 1])。对于算法PF1，给定真实的观测噪声分布；对于算法PF2，给定观测噪声分布是协方差为R0=Σ1=diag([1 000,(3π/180)2,(30π/180)2, 1])的高斯分布。由于观测噪声服从非高斯分布，因此在ORPLF算法中，Huber函数的调谐参数为μ=1.345。ONRPLF算法中L=50，Huber函数的调谐参数的初始值同样取μ=1.345，更新调谐参数μ时二分法求近似解的精度为±0.02。图2给出了这些算法在已知准确噪声协方差时的RMSE，表2给出了它们的RMSE平均值。

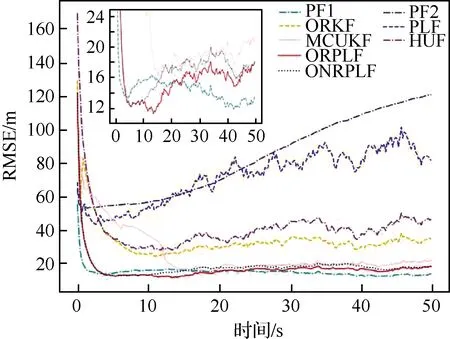
图2 已知准确噪声协方差时的仿真

表2 已知准确噪声协方差的算法平均RMSE

从表2中可以发现：PF2的平均RMSE最大，这是因为粒子滤波利用了错误的噪声先验信息；获得了准确先验的粒子滤波算法PF1的平均RMSE最小；而本文算法ORPLF和ONRPLF的性能最接近PF1；本文算法ONRPLF的性能略差于ORPLF，这是因为箱线图法估计的噪声协方差参数不可避免有一定误差，因此也就制约了滤波器的性能。

在图2中，小图展示了RMSE范围在10～25 m 之间的图形细节。从图2中可以发现：本文算法ORPLF和ONRPLF收敛较之PF1较慢；MCUKF最终也达到了接近ONRPLF的性能，但是它收敛较之本文算法更慢。在10～40 s的时间区间内，ONRPLF与ORPLF的性能出现了差距，在40 s之后这一差距逐渐消失。这是因为ONRPLF中进行一次参数估计的观测序列块的长度是L=50，由于采样率为5 Hz，因此每10 s本文ONRPLF算法就对Huber函数相关参数进行一次估计，而10 s则是第一次估计结果改变发生的时刻。随着估计参数的不断更新，本文ONRPLF算法就获得了越来越准确的噪声协方差和异常值概率，因此后续的滤波性能也就更好了。

3.3 噪声协方差存在误差的仿真

在本节的仿真实验中，仍取异常值出现的概率为ε=0.4。然而，此时先验的噪声协方差都存在误差。由于观测噪声属于非高斯分布，因此在ORPLF算法中，Huber函数的调谐参数取值为μ=1.345。在ONRPLF算法中，观测序列块的长度L=50，Huber函数的调谐参数的初始值为μ=1.345，更新μ时二分法求近似解的精确度为±0.02。

若给定3组观测噪声协方差，它们分别是真实的观测噪声协方差的λ(λ=2,4,10)倍，则得到如图3和表3所示的结果。

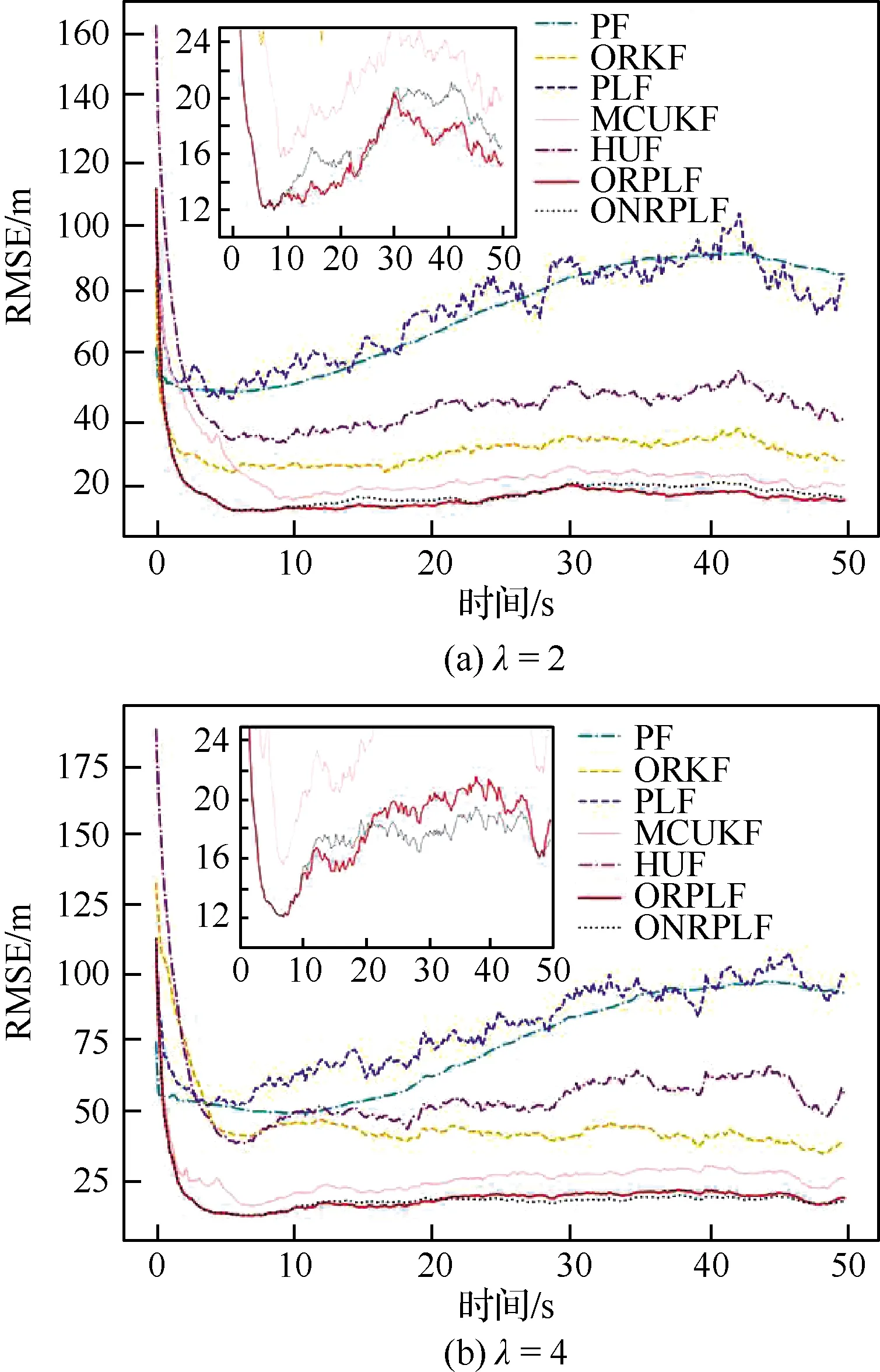
图3 噪声协方差存在先验误差的仿真1

在表3中，可以发现：当先验的噪声协方差存在误差时，本文两种算法ORPLF和ONRPLF具有最小的平均RMSE，表现出了最佳的性能。此外，给定噪声协方差与真实值的误差越大，ON-RPLF算法相较于ORPLF算法的优势就越明显，这是因为该算法中参数估计步骤起到了关键的作用。而当给定噪声协方差仅为真实值2倍时，ORPLF的平均RMSE甚至优于ONRPLF，这是由于ONRPLF中以箱线图法估计噪声协方差的误差，导致了其滤波性能的下降更显著于ORPLF使用的有误差的噪声协方差。在表3中，PLF、ORKF、MCUKF和HUF算法受观测噪声协方差误差的影响，都存在不同程度的性能下降；PF算法则极易受先验信息误差的影响。

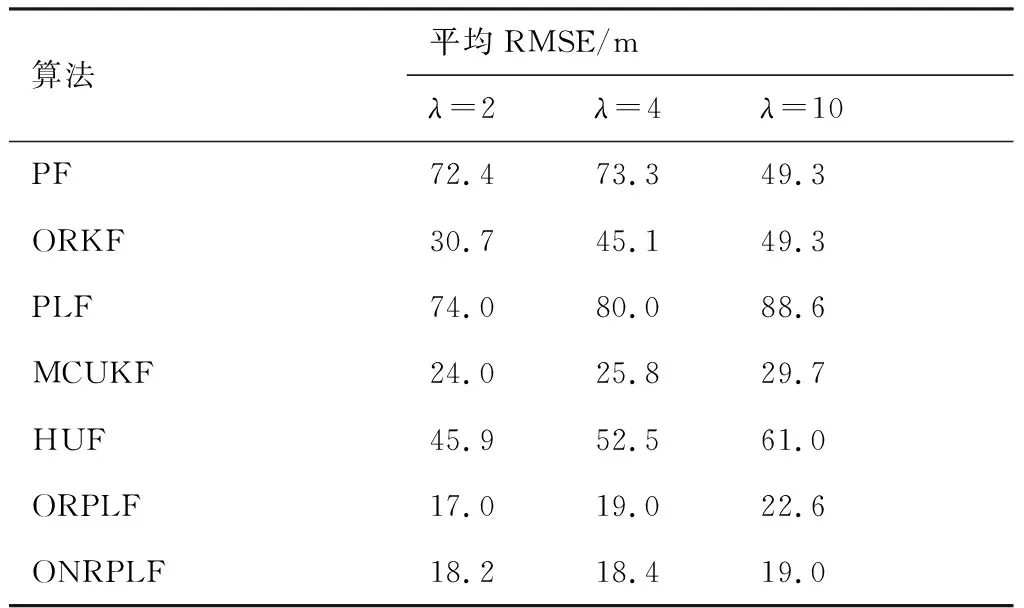
表3 噪声协方差存在先验误差的算法平均RMSE(仿真1)

在图3(a)和图3(b)中，小图展示了RMSE范围在10～25 m之间的图形细节。从图3中可以清晰地看到，随着给定噪声协方差与真实值的差距增大，算法收敛之后，ONRPLF相较于ORPLF的优势越来越明显，而其他算法的性能皆不如本文的两种算法，这与表3中得到的结论一致。从时间上来看，在10 s之前，ORPLF与ONRPLF之间的差距不明显，在10 s之后开始出现差距。在图3(a)中，ONRPLF的性能在10～20 s区间内弱于ORPLF，在20 s之后逐渐赶上，在30 s 之后又出现了差距；在图3(b)中，ONRPLF的性能在10～20 s区间内略弱于ORPLF，在20 s 之后性能超越了ORPLF；在图3(c)中，ONRPLF在10 s之后性能就超越了ORPLF，并且差距越来越大：总之，在10 s之后，随着时间的推移，观测数据量不断增加，此时，相较于ORPLF，ONRPLF的性能越来越好。正如3.2节中的分析，这是因为在本仿真实验中，每10 s本文ONRPLF算法就对背景高斯噪声的协方差及异常值概率进行一次估计，并据此更新Huber函数相关参数，而10 s正是进行第一次参数估计的时刻。随着估计参数的不断更新，本文ONRPLF算法就获得了越来越准确的噪声协方差和异常值概率，因此后续的滤波性能也就更好了。

再给定3组观测噪声协方差，它们分别是真实的观测噪声协方差的0.5、0.2、0.1倍，则得到如图4和表4所示的结果。

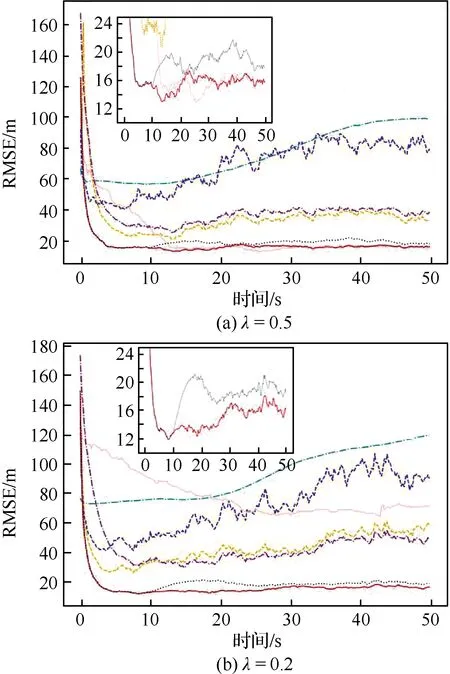
图4 噪声协方差存在先验误差的仿真2

在表4中，本文两种算法的性能仍是最佳的。与表3不同的是，ONRPLF算法的性能始终稍弱于ORPLF算法，这一方面是因为ONRPLF算法中采用箱线图法进行参数估计不可避免存在误差；另一方面是观测噪声协方差给定为真实值的0.5、0.2、0.1倍时，实际上与真实值的差异并不大，而ORPLF算法的鲁棒性确实极佳，在这样的先验信息差异下仍能保持较好的性能。

表4 噪声协方差存在先验误差的算法平均RMSE(仿真2)

在图4(a)和图4(b)中，小图展示了RMSE范围在10～25 m之间的图形细节。在图4中，相较于ORPLF、ONRPLF在10～20 s区间内都出现了不同程度的性能下降，在20 s之后两种算法的差距逐渐减小。正如3.2和3.3节中的分析，这是由于在本仿真实验中ONRPLF算法更新Huber函数相关参数的时间间隔是10 s，而10 s 正是进行第一次更新的时刻。随着估计参数的不断更新，Huber函数相关参数获得了更优的估计，因此ONRPLF的性能将逐渐提高。在图4中，PLF和HUF在先验信息存在差异时都表现出了不同程度的性能下降，但其鲁棒性较之ORKF算法更好；PF算法受先验信息的误差影响较大；MCUKF算法则极易受观测噪声协方差误差的影响，当先验信息误差较大时性能下降十分明显。

3.4 计算复杂度分析

为了比较这些算法的计算复杂度，在3.1节的仿真实验中，记录了每一种算法运行所需的平均运行时间，其结果如表5所示。仿真实验的平台为64位Win10操作系统，内存8 GB，Intel处理器，内核i7-4790，CPU3.6 G，IDLE为Python3.8。

在表5中，PF的平均运行时间远远超过其他算法，这是该算法为了达到低误差付出的运算复杂度代价。此外，与其他的滤波算法不同，PF适用于任何分布的噪声，而非像其他算法一样仅适用于高斯噪声与异常值混合这种特定的分布。本文两种算法ORPLF和ONRPLF的平均运行时间与MCUKF相近，而远低于ORKF、PLF和HUF。在本文两种算法中，ONRPLF的平均运行时间又略高于ORPLF，这是因为相较于ORPLF算法，ONRPLF算法多了参数估计的步骤。

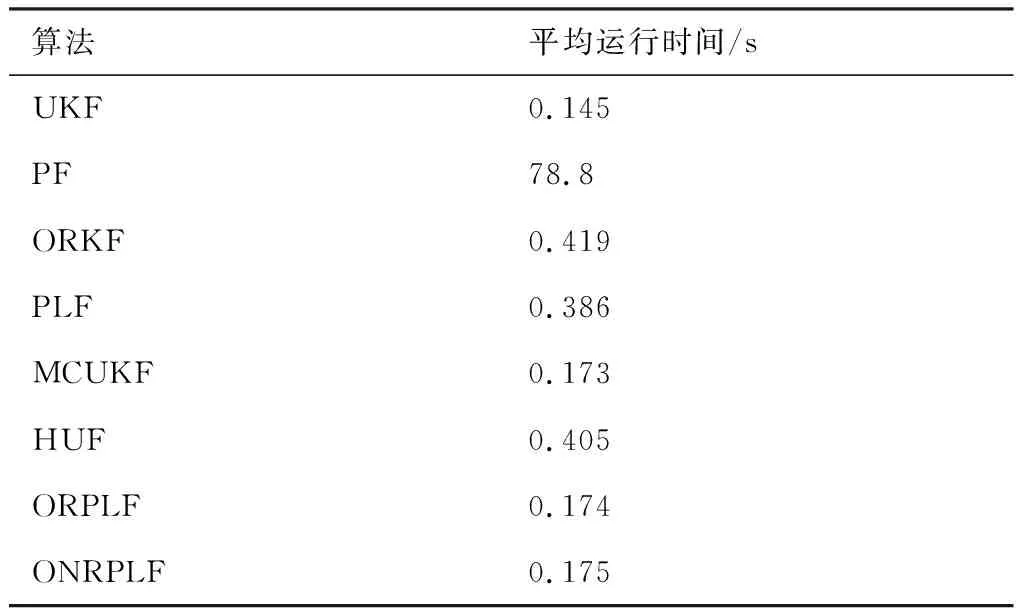
表5 算法运行时间比较

4 结 论

针对含异常观测值的非线性系统滤波问题，本文提出了两种鲁棒的滤波算法ORPLF和ONRPLF。

1)分析表明：由于Huber函数兼顾了l1范数的鲁棒性，因此用Huber损失函数代替推导PLF的MAP准则中观测误差的l2范数，构造出了一种新的准则函数，并由此推导出的ORPLF算法对异常值具有鲁棒性。

2)ORPLF仅适用于随机噪声的分布参数已知的情况，滤波器的参数由先验给定；当随机噪声的分布参数未知时，可利用箱线图法检测异常值，并进行Huber函数的相关参数估计，动态地调整滤波器的参数，这样就得到了ONRPLF算法。

3)仿真验证了分析结果的有效性，同时也表明：在观测噪声统计分布未知且含异常观测值的环境中，本文算法性能优于现有文献报道的非线性滤波类算法。