基于激光跟踪仪测量摇篮式五轴加工中心回转半径方法
闫 磊,王 萌,朱烨繁
(南阳理工学院 a.智能制造学院;b.数理学院,河南南阳 473003)
0 引言
当下,高性能数控加工技术成为现代机械加工领域的一个重要部分。多轴数控机床,特别是五轴机床是一种典型的高性能数控机床,广泛用于各种零件的加工,尤其可以满足航空航天等领域高效率和高精度的加工要求[1]。
由于机床加工和装配过程中不可避免的几何误差,在加工过程中会出现运动误差,最终影响工件的加工精度[2]。如何提高多轴加床的加工精度,特别是在长时间工作过程中保持较高加工精度,是一个关键问题[3-4]。误差补偿技术是提高机床加工精度的一个有效的方法。然而,机床误差补偿的前提是机床误差的测量[5-6]。
相比于三轴机床,五轴机床在三个直线轴的基础上增加了两个旋转轴。摇篮式AC回转工作台五轴加工中心是在直角坐标系的基础上,工件可以实现绕Z轴旋转,绕X轴旋转。两个旋转轴垂直相交,旋转轴在X轴,Z轴两个方向上的偏差值对于五轴加工中心,特别是具有五轴联动功能的加工中心有着至关重要的作用。薛佟等[7]使用千分表对摇篮式五轴加工中心进行旋转轴零位和旋转轴偏移进行测量;李亚东等[8]对摇篮式五轴加工中心机床进行精度标定;唐清春等[9]提出一种RTCP插补算法来减小非线性误差从而提高五轴加工中心加工精度。然而,传统的测量方法效率低、精度低,无法满足日新月异的高档数控机床精度要求。
激光跟踪仪是一种大型坐标测量仪,具有操作简单、测量精度高、效率高等优点,广泛应用于船舶、汽车、机床等领域[10-11]。余苏等[12]使用激光跟踪仪对重型装备进行在线测量;Wang J等[13]使用激光跟踪仪实现了多轴数控机床旋转轴与直线轴相对位置关系的识别;Wang J等[14]提出一种使用激光跟踪仪对多轴数控机床进行全向误差检测;李金川[15]基于激光跟踪仪实现了数控机床几何误差的快速高精度检测。
但是,以往的研究和技术没有使用激光跟踪仪实现对AC摇篮式五轴加工中心回转半径的测量。为了解决对五轴加工中心回转半径的测量,提出一种基于激光跟踪仪的测量方案,并在此基础上提出了测量精度提升方法,对于提高五轴加工中心旋转轴回转半径测量精度和效率具有积极意义。
1 测量原理
本文使用激光跟踪仪测量五轴加工中心A轴回转半径,测量原理如图1所示。

图1 试验平台及原理示意图
测量步骤:
(1) 确定工作台平面方程:加工中心工作台A轴回零,使用激光跟踪仪配合靶标,在工作台平面选择若干个点,记录目标点坐标值,根据坐标值拟合平面方程。
(2) 确定A轴回转轴方程:将激光跟踪仪靶标固定在工作台任意位置,旋转A轴,并在不同位置记录靶标坐标值,根据坐标值拟合圆方程,得到圆心坐标和半径;将激光跟踪仪靶标固定在工作台另一位置,重复上述步骤,得到若干个圆心坐标和半径值;根据得到的若干个圆心坐标值,拟合A轴直线方程。
(3) 确定回转半径:根据第(1)步和第(2)步得到的工作台平面方程和A轴回转轴直线方程,利用空间直线到平面的距离公式计算回转半径。
1.1 工作台平面方程
根据三点确定一个平面的基本几何原理,在A轴回零的基础上,使用激光跟踪仪结合靶标测量工作台平面上任意三点坐标,记为P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3)并设平面方程为:
Ax+By+Cz+D=0
(1)
可得:
(2)
其中,
D=-(A·x1+B·y1+C·z1)
(3)
由此,根据工作台上三个激光跟踪仪靶标位置坐标可以得到工作台平面方程,如公式(1)所示。
1.2 回转轴直线方程
将激光跟踪仪靶标固定在工作台任意位置,转动工作台A轴,分别记录三个不同位置坐标值,记为:PA1(xA1,yA1,zA1)PA2(xA2,yA2,zA2)PA3(xA3,yA3,zA3),设圆心坐标为:CA0=(xA0,yA0,zA0),并设半径为rA。由PA1,PA2,PA3共面,得到如下方程:
(4)
得到共面方程为:
AAx+BAy+CAz+DA=0
(5)
其中,AA,BA,CA,DA为共面方程的参数,可根据1.1节工作平面方程参数确定方法求得。由三点到空间圆心坐标的距离相等约束得到:
(6)
式(6)消去rA并结合共面方程,可以得到圆心空间坐标线性代数方程组:
(7)
其中,
解得圆心坐标为:
(8)
同样的方法,在工作平面另一点,固定靶标,转动A轴,记录三个点PB1(xB1,yB1,zB1)、PB2(xB2,yB2,zB2)PB3(xB3,yB3,zB3),并设圆心坐标为CB0=(xB0,yB0,zB0),可解得圆心坐标为:
上式中所有参数确定方法与前述方法一致,不再赘述。由圆心CA0,CB0可得A轴回转轴的直线方程为:
(9)
1.3 回转半径
由AC轴转台几何关系知,当工作台绕A轴转动时,A轴回转轴始终平行于工作台平面,则回转半径即为A轴回转轴到工作台平面的距离。理论上,假设建立在所形成的回转圆所在平面与工作台平面垂直,利用第一个回转圆到工作台平面的距离也可以表示回转半径。实际上,如果能尽可能多地形成多个回转圆,使用回转圆圆心拟合回转轴直线,弱化因回转圆平面与工作台平面不垂直引起的误差,但是同时增加工作量。因此,本文在权衡精度与测量方法的工作量后,选择工作台两端形成两个回转圆来拟合回转轴直线方程。根据工作台平面方程和回转轴直线方程,回转半径r表示为:
(10)
其中,(x1,y1,z1)为工作台平面上任意一点,(x2,y2,z2)为A轴回转轴直线上任意一点。
1.4 误差分析与精度提高方法
由式(10)知,回转半径由回转轴直线方程和工作台平面方程参数确定,上述方程参数的拟合精度与拟合这些方程的点的个数有关。在回转半径公式理论推导过程中,工作台平面方程、回转圆心的确定仅仅使用三个点来确定方程。另外,由于激光跟踪仪存在测量误差,为了提高测量方法的精度,在确定平面方程以及回转圆心坐标的时候,增加采样点个数,提高拟合精度,以此来提高测量精度。在此基础上,提出一种基于奇异值分解和最小二乘优化圆心拟合方法来提高拟合精度。具体做法如下所述:
假设有n个采样点P0,...,Pn-1,其中Pi=(xi,yi,zi)T∈R3,为了得到一个尽可能接近这些点的圆,参数方程表示为:
P(t)=rcos(t)u+rsin(t)(n×u)+C,0≤t≤2π
(11)
其中,r为半径,C为圆心坐标,n为单位法向量,u垂直于n。用天顶角φ和方位角θ指定圆在空间中的方向,得到:

(12)
拟合式子(11)表示的圆,按以下步骤进行:
(1)使用SVD(奇异值分解)找到与均值中心点集最匹配的平面。

(13)
使用奇异值分解将矩阵A分解为A=UΣVT,其中U,V为酉矩阵,Σ为对角阵,包含奇异值σ1≥σ2≥σ3≥0。由此可得:

(14)
其中,引入b=VTn。由于σ3为最小的奇异值,因此取b=(0,0,1)T可以最小化公式(14)。并且可以得到单位法向量n。

(15)

(2)在新的2D坐标中将均心点投影到拟合平面上。
使用罗德里格斯旋转公式将三维点映射到一个新的拟合平面,选择旋转轴K为平面法向量和新的拟合平面发向量之间的矢量积。因此,K=n×(0,0,1)T。映射到新平面的点的坐标为
Prot=Pcos(θ)+(k×P)sin(θ)+
k
(16)
(3)使用最小二乘法在2D坐标中拟合一个圆并获得圆的中心和半径。
定义二维平面半径为r,圆心为(xc,yc)T的圆方程为:

(17)
其中,引入c=(c0,c1,c2)T作为未知参数。带入所有的二维平面输入点,得到如下线性方程:
Ac=b
(17)
其中,
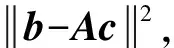
(4)将圆心转换回3D坐标,拟合圆由其中心,半径和法线向量指定。
根据罗德里格斯旋转公式,将圆心坐标映射到三维空间,不再赘述。
2 试验平台及测量方法
试验需要的设备有:EUMASPINNER DU5-650五轴加工中心,莱卡AT930激光跟踪仪,靶标,计算机。见图2。

图2 试验设备及现场
试验实施步骤:
固定并校准激光跟踪仪,将激光跟踪仪靶标分别按照测量工作台平面、测量回转轴直线要求安装在五轴加工中心工作台上。分别进行以下两组试验:
(1) 将激光跟踪仪靶标安装在工作台平面,加工中心A轴、C轴回零;按照5°间隔转动C轴,转动360°,每个位置记录一次靶标位置,共计72组。
(2) 将激光跟踪仪靶标安装在工作台平面,加工中心A轴、C轴回零;按照1°间隔转动A轴,转动120°,每个位置记录一次靶标位置,共计120组。然后将激光跟踪仪靶标安装在工作台另一任意位置,加工中心A轴回零;按照1°间隔转动A轴,转动120°。每个位置记录一次靶标位置,共计120组。
3 试验结果及分析
根据步骤(1)、(2)的操作方法,分别得到用于拟合工作台平面、回转圆1和回转圆2的数据,见图3。坐标点及拟合结果见图4。回转轴拟合结果见图5。

图3 激光跟踪仪靶球原始坐标点

(a)坐标点 (b) 工作台平面拟合结果

(c)回到圆1拟合结果 (d)回转圆2拟合结果 图4 坐标点及拟合结果

图5 回转轴拟合结果
3.1 工作台平面方程拟合试验
根据实验得到的数据,考虑靶球半径补偿之后,根据测量原理工作台平面方程拟合方法,拟合结果见表1。
得到工作台平面方程为:
0.001906x-0.003333y+0.999993z+292.59=0
(19)
3.2 回转轴直线方程拟合试验
步骤(2)得到两组靶球坐标,分别用于拟合第一个回转圆和第二个回转圆。考虑靶球半径补偿之后,根据1.4节空间圆拟合方法,两个回转圆的拟合结果见表2。
由此,拟合出来的两个圆的圆心坐标经过的直线,也就是回转轴直线方程为:
(20)

表1 工作台平面拟合结果

表2 回转圆拟合结果
3.3 回转半径计算结果及分析
步骤(1)和步骤(2)分别得到工作台平面的拟合方程和回转轴直线方程,见公式(19)和公式(20)。1.3节给出了回转半径的计算公式,见公式(10)。根据公式(10),任意选择工作平面上一点和回转轴直线上一点,得到回转轴半径为49.994 mm。
利用传统的基于机械式百分表的测量方法,对试验用五轴机床进行回转半径测量,并与提出的方法进行对比验证。机械式百分表测量结果为49.843 mm,与本方法测量结果有0.151 mm的误差。分别用两次试验结果补偿五轴加工中心回转半径,并对加工的标准件进行测量发现,本文提出的方法测量结果更加精确,且步骤简单。
4 结论
精确的摇篮式五轴加工中心回转半径对于五轴加工中心实现精确的五轴联动加工具有重要意义。本文基于激光跟踪仪对AC摇篮式五轴加工中心A轴回转半径进行测量。由于激光跟踪仪的使用,简化了传统使用千分表测量回转半径的方法,提高了测量精度,解决了困扰回转半径测量的技术难题。在测量原理分析的基础上,给出了提高测量精度的方法及数据拟合算法。基于激光跟踪仪的摇篮式五轴加工中心回转半径测量方法作为一种全新的数字化测量方法值得推广应用。

