基于多特征融合的零件分类与姿态识别*
陈宪帅,吴自然,闫俊涛,吴桂初,郭天慧
(1.温州大学乐清工业研究院,浙江 温州 325000;2.襄阳市供电公司,湖北 襄阳 441000)
0 引言
随着工业生产中对机器自动化、智能化需求的日渐提高,机器视觉作为工业生产向智能化方向发展的重要技术之一,已得到愈加深入的研究,越来越多的视觉检测、测量及定位等技术被应用到实际生产当中[1-3]。但基于机器视觉的智能制造技术的发展,其可行及可靠性依靠高精度的图像分类、识别和定位跟踪等技术来支撑,而生产中所面临的形色多样的生产对象、复杂的工业环境及其不同的功能要求,给视觉的识别处理工作带来极大的困难和挑战。
随着视觉技术在工业生产中的需求日益增加,越来越多的基于视觉的分类、识别及定位方法被提出。孔令聪[4]提出了一种以零件轮廓的形状、面积和周长等特征参数对零件进行分类,后计算零件的质心等参数对零件进行定位及姿态估计的方法;徐远等[5]采用两个单目相机,通过改进NCC匹配算法的一次定位和基于边缘特征的模板匹配进行二次定位实现了对工件和装配孔的两次定位;曹冬梅等[6]通过对条烟图像的边缘与模板进行匹配,从而进行定位与姿态估计,再用相关性、对比度和各向异性等特征训练支持向量机分类模型对目标进行分类;曾鹏[7]首先在虚拟空间每隔一定步长渲染工件的CAD模型进行模板库的建立,然后根据实时采集的图像与模板库匹配获得工件的粗略位置姿态参数,在第二步的精确姿态参数求取中使用L-M算法进行迭代,获得较为精确的工件位置姿态;周逸徉[8]利用深度图像进行分割,再利用颜色数据提取HOG特征进行SVM分类,然后通过三维点云配准定位可抓取位置。综上所述,在面对复杂程度相对较低的识别对象时,可以利用轮廓、面积与质心等信息进行分类,并直接定位抓取点坐标和对姿态进行估计,但当识别对象复杂程度较高时,便无法直接通过这些参数对抓取点及姿态进行估计。此外,以支持向量机等建模的方法进行分类,当对象越多、越复杂时,模型训练所需的数据量也就越大,极大地延长了开发周期[9-10]。
针对工业应用中的视觉技术并考虑上述问题,以小型断路器柔性装配系统为实例,提出一种综合物体自身及其成像的多特征融合的识别方法。以单目相机成像,完成对目标零件的分类、姿态识别和抓取定位工作。
1 系统方案与硬件组成
1.1 系统方案介绍
基于机器视觉的小型断路器柔性装配系统由视觉识别系统和机器人运动系统及零件等部分组成。通过视觉分类识别出散放零件的种类及摆放姿态,定位零件抓取坐标,从而引导机器人完成对零件姿态的调整及后续的装配工作。其系统框图如图1所示。

图1 柔性装配系统框图
1.2 系统硬件组成
系统硬件如图2所示。为降低相机对识别精度的影响,选用分辨率为2590×1942的Basler相机,其分辨率高于常规机器视觉系统中使用的相机。为使散放的零件均能落入相机视野同时不影响机器人动作,相机安装高度为60 cm。系统主控制器为机器人控制器,其作用有:接收光电开关输入的零件到达信号、输出相机开始拍照信号以及对机器人运动和气缸夹爪动作的控制信号。

图2 系统硬件图
2 多特征融合匹配的识别算法
为便于不同种类零件及同种类不同摆放姿态的分类识别,首先规定使用两级分类编号如图3所示。
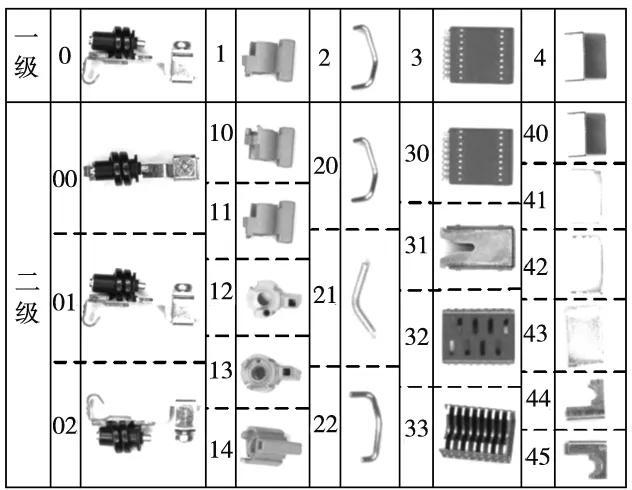
图3 类别编号示意图
视觉识别算法流程如图4所示。

图4 视觉识别算法流程图
从获取图像到向机器人控制器发送数据的过程中:首先需对场景中不同种类零件及各类零件不同摆放姿态做出分类判断;然后通过匹配当前状态零件与目标状态零件两幅图像中关键点的方式求取零件的旋转角度;继而用获取到的关键点对计算出两幅图像的仿射变换矩阵,用以计算指定的抓取点在当前状态零件图像中的像素坐标;最后使用通过相机标定与手眼标定得到的变换矩阵,将求取的抓取点像素坐标变换成机器人坐标系下的空间坐标[11]。
2.1 图像预处理
预处理包括灰度化、边缘提取、二值化、形态学操作、轮廓提取及最小矩形框拟合等步骤将场景中的5类零件从源图中分割,用以后续的分类及识别工作。如图5所示,针对以绿色最小矩形框无法直接分割图像,而零件相距较近时,以矩形框分割则出现如图6a所示,将非目标零件部分同时分割至一张图中的问题,其解决步骤如下:
(1)创建与蓝色框同等大小的背景图像;
(2)将绿色最小矩形区域内像素点坐标减去蓝色矩形框左上顶点坐标构成新像素点,同时将其三通道灰度值赋予新像素点;
(3)将新像素点画入创建的背景图像中,其分割效果如图6b所示。

图5 零件矩形框选图

(a)蓝色框分割效果 (b)改进后分割效果图6 切割效果对比图
2.2 零件一级分类
一级分类通过对零件最小矩形框的面积、轮廓面积以及颜色特征等进行分析比较做出类别判断。其算法流程如图7所示。S0为分割后第一个零件的最小矩形框面积,用以初始化变量max_S和min_S,而Sn则是另外4个零件的最小矩形框面积。Th1、Th2分别为绿色与红色像素数的参考阈值。Sr1、Sr2分别为图片3和4代表的零件最小矩形框面积。
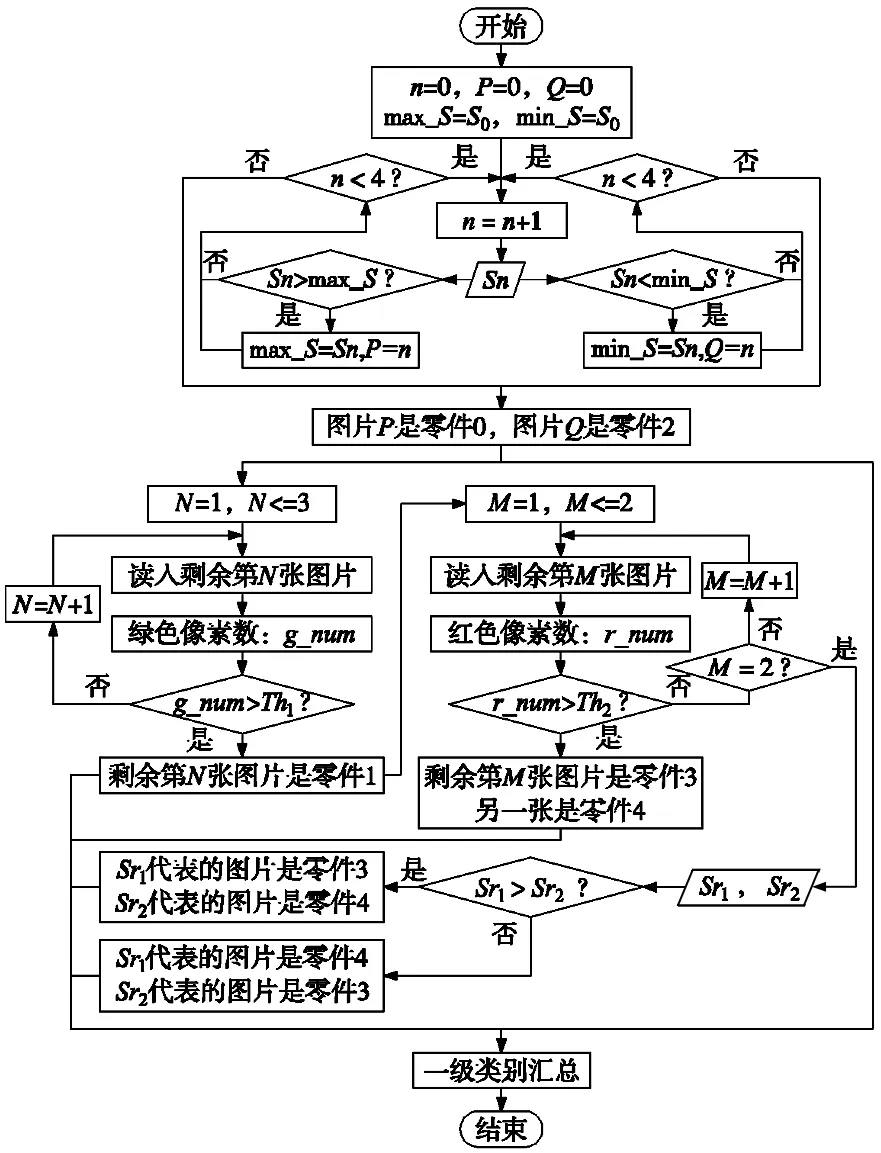
图7 一级分类算法流程图
2.3 零件二级分类
二级分类通过对零件自身在不同摆放姿态下的最小矩形框面积、颜色、成像以及固有特征等信息的比较依次做出类别判。
(1)零件0:如式(1),比较零件0最小矩形框面积max_S与给定阈值Th3的大小,其分类结果lab0记作:
(1)
对姿态01、02则通过零件成像特征来区分。如图8a和图8c所示,对矩形框可能出现的两种情况,以P1点为基础点,判断P1P2与P1P3的长短情况,并按式(2)重新规定4个顶点的顺序,如图8b和图8d所示。
(2)

(a)横向框 (b)阴影区域 (c)纵向框 (d)阴影区域图8 最小矩形框示意图
以Q1Q2所在的长边划定感兴趣区域(ROI),如图8b和图8d阴影区域所示。假设表示零件的像素点集合为S,感兴趣区域内像素点集合为s,通过式(3)对感兴趣的矩形长边做出选择,记作L:
(3)
对选取的边L的两个端点,即顶点,以类似边选取的方式做出选择。如图9所示,实际操作中A点为最终选取的感兴趣点,同时记录与其构成矩形短边和长边的B、C两点。设向量AB和AC的夹角为φ,因在图像中顺时针转动角度为负,反之为正,所以根据式(4)做出类别判断,记作:
(4)

(a)姿态01ROI (b)三点 (c)姿态02ROI (d)三点 图9 操作示意图
(2)零件1:其算法流程如图10所示。Th4为零件1在自身不同姿态下的绿色像素数参考阈值,Th1与其的区别在于,Th1为自身与其它零件比较的参考;Th5为自身轮廓面积的参考阈值;小圆如图11a中标记的圆,与图11b形成对比。

图10 零件1二级分类流程图
子流程‘姿态10or11’的步骤同零件0姿态01和02的区分步骤基本一致。但零件1选取的感兴趣边为矩形框的短边,且依据是两条短边与质心点m距离的大小。实际操作如图11c、图11d所示,选取的边为AB边,点为A点。其分类结果lab1记作:
(5)
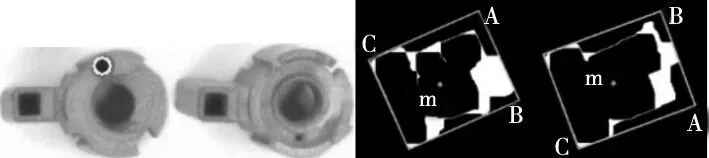
(a)小圆 (b)无小圆 (c)姿态10 (d)姿态11图11 操作示意图
(3)零件2:如式(6),比较零件2最小矩形框面积min_S与给定阈值Th6的大小,其分类结果lab2记作:
(6)
如图12所示,对零件轮廓进行凸包检测找出其中间弯曲处的弯曲点O。同样以零件0中边选取的方式找到AB边所在,而两种姿态下均有矩形框顶点A距离O点较近,从而确定A点所在。设向量OA和OB的夹角为φ,分类结果如式(7),记作:
(7)
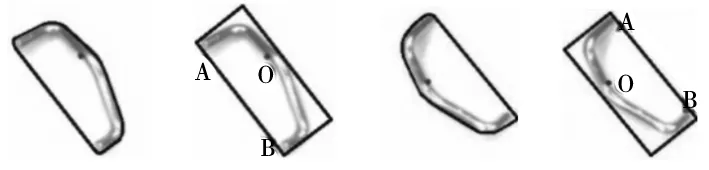
(a)姿态21凸包 (b)三点 (c)姿态22凸包 (d)三点图12 操作示意图
凸包即如图12a和图12c中的蓝色包围线,为凸多边形,凸包所包围白色区域即为凸性“缺陷”。
(4)零件3:依据零件3在一级分类中是否通过红色提取判断作出进一步判断,算法流程如图13所示。s3为其最小矩形框面积,Th7为姿态30和32的区分阈值,Th8为姿态31和33的区分阈值。
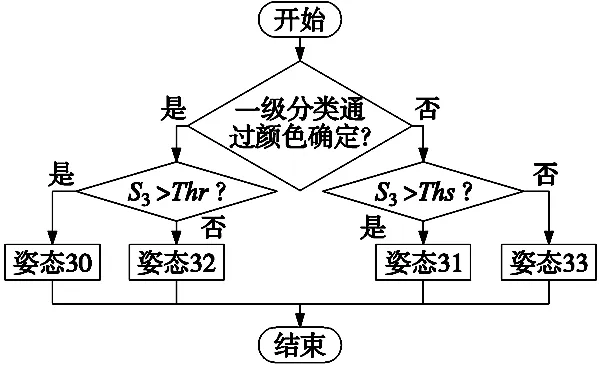
图13 零件3二级分类流程图
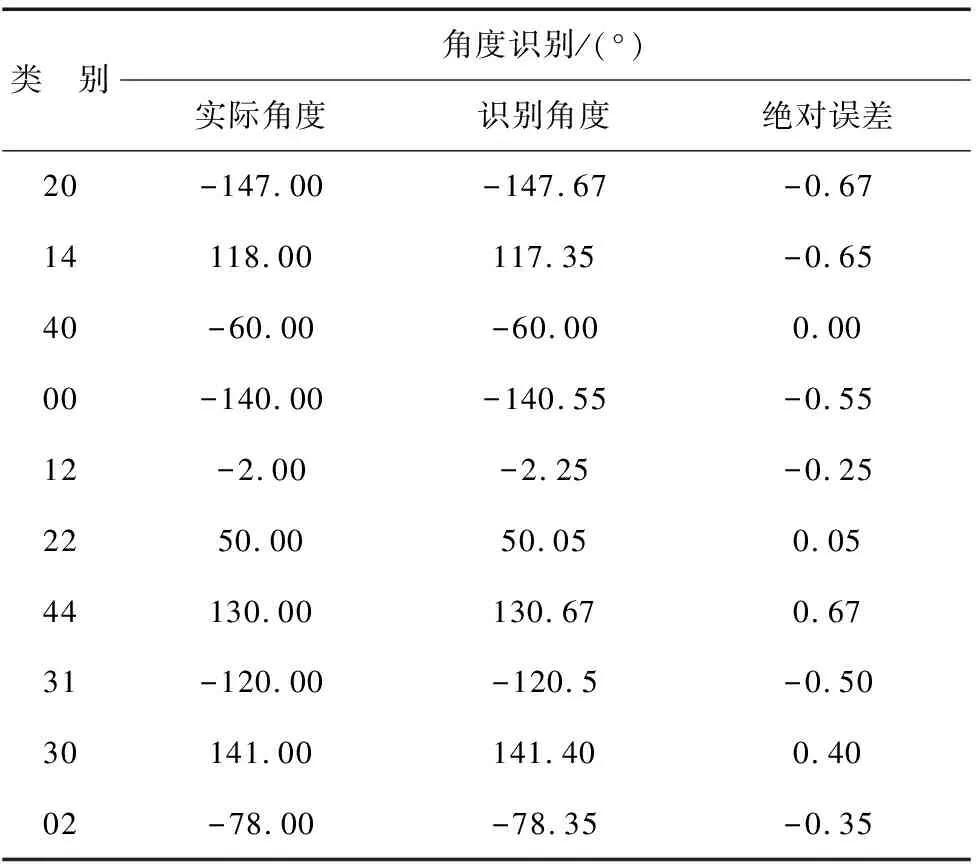
(5)零件4:如式(8),比较零件最小矩形框面积s4与给定阈值Th9和Th10的大小,Th9 (8) 对于姿态41、42和43,如式(9),比较零件轮廓面积Scnt与给定阈值Th11的大小,将其分为两个子类,记作: (9) 如图14所示,姿态41和42在灰度、形状、边缘梯度等方面均存在极大的相似度,难以准确区分,因此采用机械的方式使其变为姿态40或43再进行角度识别。 图14 姿态:左41 右42 对于姿态44和45:顺次对矩形框顶点划定感兴趣区域,满足式(10)表述的条件,即确定为感兴趣顶点。其中S为零件像素点集合,s为感兴趣区域内像素点集合。 S∩s=∅ (10) 回缩矩形框,获取新矩形区域内的零件轮廓点;比较获取的轮廓点与不以感兴趣顶点为端点的两条原矩形框的边的最小距离的大小从而确定两条边的位置。实际操作如图15所示,感兴趣顶点为A,与回缩后矩形框内轮廓点最小距离较小的边为BD边,另外一边即为CD边。设向量AB和AC的夹角为φ,根据式(11)做出类别判断,记作: (11) (a)姿态44 (b)四点示意 (c)姿态45 (d)四点示意 图15 操作示意图 通过对矩形框中感兴趣的边以及感兴趣的顶点位置的分析,提取用以计算旋转角的关键点,即与各顶点距离最近的轮廓点。其算法流程大致如图16所示。 图16 角度识别算法流程 大部分姿态感兴趣边或顶点的选取过程同零件0姿态01和02、零件2姿态21和22以及零件4姿态44和45等区分过程中的边、点选取过程基本类似,只是选取的方法略有不同,便不再赘述,匹配效果如图17a~图17c所示。对于图像具有对称性的姿态,则无需进行边或点的选取,可在区分出矩形框长短边后直接进行顶点顺序的规定,如图17d所示零件3姿态32;而对于特征点易抓取的姿态,如零件1姿态12和13,可通过圆检测和矩形检测提取关键点用以计算角度,同时也可做抓取点。其效果如图17e和图17f所示。 (a)姿态00 (b)姿态20 (c)姿态40 (d)姿态32 (e)姿态12 (f)姿态13图17 匹配效果图 综上所述,角度计算如图18所示,计算实际图像中两个关键点的向量ac及对应模板中的向量a1c1,其夹角θ即为旋转角。为减小误差,尽可能求多个值取平均。实际中,应提前对模板图像进行关键点的提取与保存,在提取到实际图像中的关键点后,直接查询对应姿态的关键点计算角度即可,减少无谓的时间消耗,从而提高算法的运行效率。 图18 角度计算示意图 机器人坐标系下的抓取点坐标通过两步获取。首先,利用至少三对关键点对计算实际与模板图像间的仿射变换矩阵,并同提前保存的对应姿态零件的抓取点在模板图像中的像素坐标作矩阵乘法,得出抓取点在实际图像中的像素坐标,如公式(12)所示;其次,利用相机标定及手眼标定获取的坐标转换矩阵,将抓取点的像素坐标变换为机器人坐标系坐标,如公式(13)所示: (12) (13) 式中,M1为仿射变换矩阵、M2为坐标转换矩阵,(u,v)为抓取点在实际图像中的像素坐标、(u0,v0)为抓取点在模板图像中的像素坐标、 (x,y,z)为抓取点在机器人坐标系下的坐标、(x0,y0,z0)则为机器人坐标系与世界坐标系间的偏移量。 搭建实验台,获取并保存零件各姿态下的模板图像及对应抓取点像素坐标,对零件分类、角度与抓取点坐标识别进行实验分析。 采集各零件各姿态样本400组进行分类实验,其分类结果如表1所示。可看出一、二级分类正确率均达到99.5%及以上,整体分类正确率在99%以上,均满足分类要求。同时,较深度学习等建模的分类方式,节省了模型训练所需的时间,使得其调整及维护更加方便高效。 表1 分类结果统计表 取30组样本,分别采用算法1:带K近邻比约束和随机抽样一致性(RANSAC)剔除误匹配的ORB特征匹配算法[12-13]、算法2:最小矩形框旋转角质心估计[4]和文章算法3对零件旋转角度进行实验。其中部分结果对比数据如表2所示。 表2 部分结果对比数据表 根据图2所示的机器人装配实验,为保证机器人能够对零件姿态进行正确的调整,要求识别的角度绝对误差在±0.8°范围以内,超出该范围则认为识别不合格。所以,文章统计3种算法下零件旋转角度计算合格的样本组数,计算合格率;同时对去除不合格情况后剩余的样本进行角度误差分析,计算各样本的绝对误差,并统计该误差绝对值的平均值。其结果如表3所示。 表3 角度识别数据分析表 从上述两表可看出,通过算法1和算法2计算角度的合格率均小于算法3,且两者在去除不合格样本后的误差平均值仍略高于算法3。综合误差精度及合格率两方面考虑,算法3的角度计算效果要优于前两者。 而造成前两种算法角度计算出现错误的原因分别为以下两点: (1)一些零件自身特征点区分不明显,匹配时易混淆却又无法剔除,如图19a所示,与文章算法匹配效果图19b形成对比; (2)由于零件的外形复杂不规则,导致一些姿态下零件最小矩形框与自身的相对位置不是固定不变的,无法通过最小矩形框的旋转角来正确描述零件本身的旋转角,如图19c所示。 (a)算法一效果 (b)算法三效果 (c)矩形框示意 图19 误差分析示意图 算法2以质心为抓取点,对于外形不规则的零件而言,质心点不一定是合理的抓取点;算法1与文章算法的抓取点坐标需依靠匹配到的特征点对来进行计算,然而,算法1的匹配效果无法满足要求,其坐标计算的准确性便无法得到保证。所以,通过文章算法对零件分类、角度识别及抓取点坐标识别进行综合实验,其部分结果如表4所示。对所列数据分析可得:角度识别的误差平均值为0.41°,x轴坐标识别的误差平均值为0.194 mm,y轴为0.256 mm,满足角度允许误差±0.8°、坐标允许误差±0.3 mm的要求。 文章提出了一种基于多特征融合匹配的分类、识别与定位方法并进行了实验分析。相比于SVM、深度学习等建模分类的方法,当零件颜色、大小或形状等信息发生变化时,无需采集大量的数据重新对模型进行训练,只需调整相关参数便能适应改变,极大地缩短了系统的开发周期,提高了开发效率;而与常见的特征匹配等算法相比,在面对姿态多样或者特征区分不明显的零件时,其匹配的稳定性高,更大程度地保证了角度与坐标计算的准确性。实验结果表明,该方法的识别精度满足实际系统的要求。 表4 部分零件样本识别结果 续表

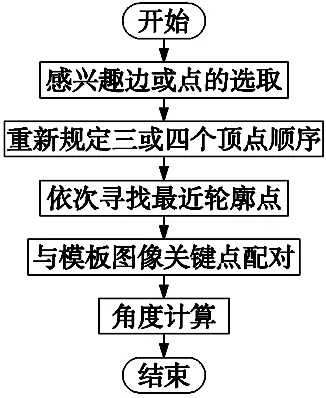
2.4 关键点提取与角度计算



2.5 抓取点坐标提取与转换
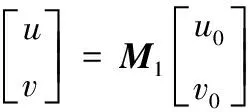
3 实验及结果分析
3.1 零件分类识别实验
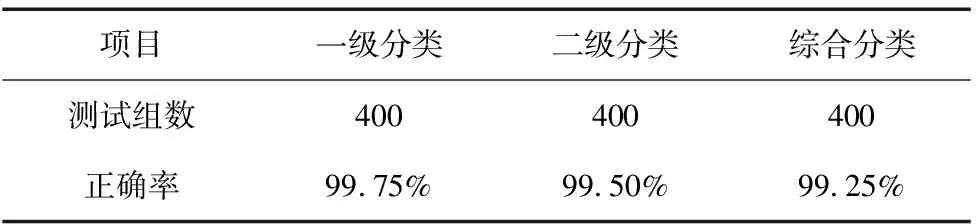
3.2 零件角度识别对比实验
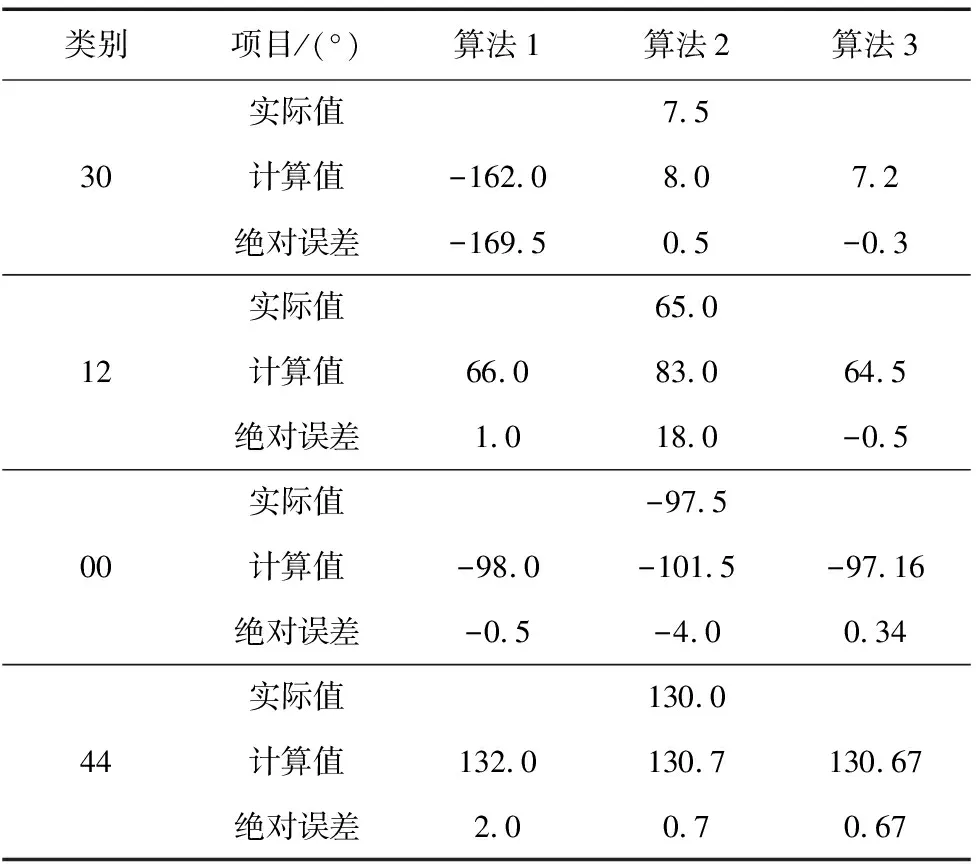
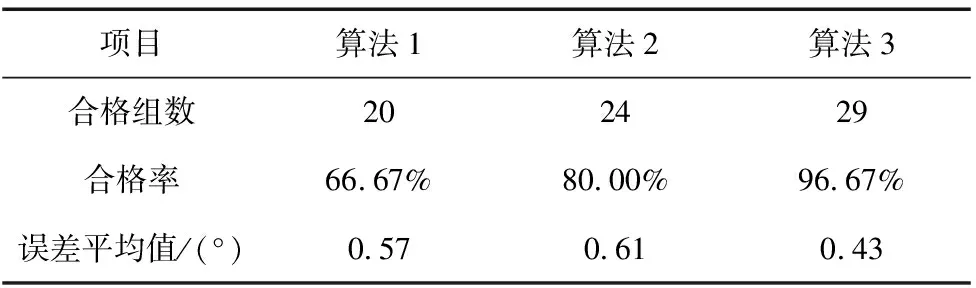

3.3 综合实验
4 结束语