基于MOOSE框架的五方程两相流分析程序开发
牛钰航,芦 韡,贺亚男,邓超群,向烽瑞,巫英伟,*,苏光辉,秋穗正,田文喜,于 洋,卢忝余
(1.西安交通大学 动力工程多相流国家重点实验室,陕西 西安 710049;2.中国核动力研究设计院 核反应堆系统设计技术重点实验室,四川 成都 610213)
在反应堆正常运行和事故瞬态工况下,气液两相流动是一个非常重要的物理现象,精确模拟两相流现象是反应堆安全分析的关键。根据两相流体流速是否均匀、两相流体温度是否处于热平衡态的假设不同,可将两相流模型分为三方程到六方程模型[1]。
现有的反应堆系统安全分析程序如RELAP5[2]、TRACE[3]已成功采用六方程模型计算两相流动传热问题。五方程模型忽略了气相能量守恒方程,并将气相温度给定为当前压力下对应的饱和温度。相比于六方程模型,虽然五方程模型没有精确反映气液两相之间的能量交换,但具有更强的适用性和鲁棒性[4]。除此之外,RELAP5、TRACE程序虽然采用六方程模型,但在时间和空间数值离散方面仍是一阶精度,即使已有研究对RELAP5数值方法进行了许多改进,如在RELAP5中增加了半隐式算法[5],但时间离散仍旧是一阶精度,使得其只适用于短瞬态过程精确模拟[6]。因此有必要开发高精度的两相流求解模型。
本文基于开源MOOSE框架初步开发一维、五方程两相流模型计算程序ZEBRA,采用PJFNK算法全耦合求解方程,并与过冷沸腾实验值进行对比。
1 程序框架简介
MOOSE[7]是由美国爱达荷国家实验室(INL)采用C++开发的多物理场耦合计算框架。MOOSE主要基于有限元方法和PJFNK算法,可高效、模块化求解偏微分方程组(PDEs)。当前,国外基于MOOSE框架已经开发出了BISION[8]、RATTLESNAKE[9]、RELAP7[10]等燃料性能分析、堆物理计算和系统分析程序。国内基于MOOSE框架已经开发出了BEEs[11]燃料性能分析程序和中子扩散问题求解程序[12]。
MOOSE框架结构示意图如图1所示。MOOSE框架包含4个层级:第1层级为开发者模块,即在MOOSE框架下构建具体物理问题,在本文中添加了基础物理模型(五方程本构方程)及与五方程本构方程对应的封闭关系式,同时集成了MOOSE中多个模块(如边界条件、物性等),实现了给定压力(如泵模型)等边界条件的构建,共同组成了五方程两相流计算模块;第2层级为MOOSE已定义模块及多物理场耦合接口模块,包含通用的边界条件等;第3层级为LibMesh,MOOSE继承开源库LibMesh进行网格读入、有限元离散、残差矩阵形成和结果输出;第4层级为求解器模块,MOOSE采用PETSc求解器求解残差矩阵。
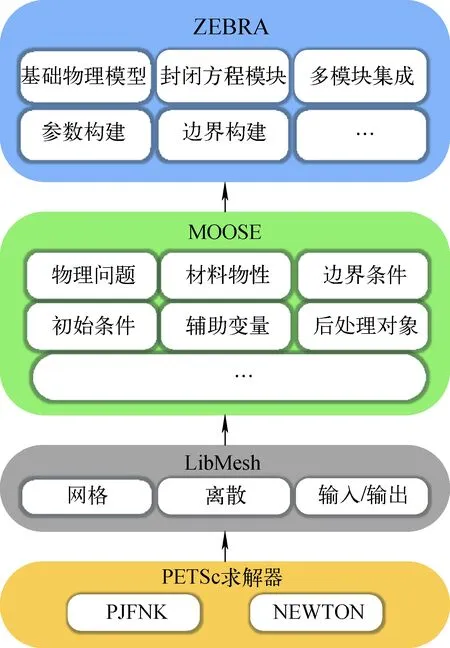
图1 MOOSE开发结构示意图Fig.1 MOOSE structure diagram
2 数学模型
一维五方程两相流模型包括质量守恒方程(气相、液相)、动量守恒方程(气相、液相)和能量守恒方程(液相)。
2.1 控制方程
质量守恒方程:
(1)
(2)
动量守恒方程:
α1ρlgx+Fint-Fwall,l-Γg(uint-ul)
(3)
αgρggx-Fint-Fwall,g+Γg(uint-ug)
(4)
能量守恒方程:
(5)
式中:α为空泡份额;ρ为密度;u为速度;t为时间;x为空间位置;Γg为相间传递的质量;p为压力;gx为重力加速度;e为内能;下标l和g分别表示液相和气相;下标int表示气液两相的交界面;Γw为壁面沸腾/冷凝过程中气相产生速率;Γig为相间气泡的质量传递;Fint为相间摩擦阻力;Fwall为各相的壁面摩擦阻力;h′为由于壁面产生蒸汽而引起质量传递的相焓;h*为交界面之间质量传递的相焓;Qwl为壁面对液相的热量传递;Qil为交界面对液相的热量传递。
式(1)~(5)中求解的5个主要变量分别为压力p、空泡份额α、液相速度ul、气相速度ug和液相内能el,即变量矩阵为:U=[p,α,ul,ug,el]T。
气相和液相的空泡份额满足关系:
αl+αg=1
(6)
五方程模型中假设气相温度Tg为当前压力下对应的饱和温度Tsat,则:
Tg=Tsat(p)
(7)
2.2 本构模型
1) 空泡份额分布
ZEBRA目前添加了垂直通道内临界热流密度(CHF)发生之前的流动传热特性模型,其空泡份额分布示于图2。其中,αBS、αSA、αAM分别为不同流型转换位置的空泡份额,且不同的本构模型(如壁面摩擦阻力、相间摩擦阻力等)有不同的流型转换空泡份额。
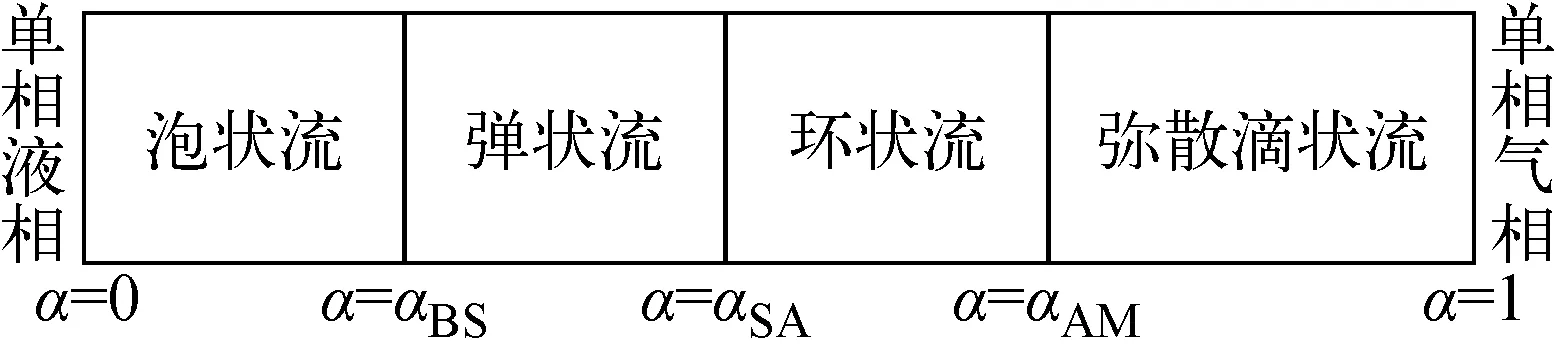
图2 垂直通道内空泡份额分布Fig.2 Distribution of void farction in vertical channel
ZEBRA添加的流型转换判定准则与RELAP5-3D、TRACE程序类似,随着空泡份额的增大,将其分为单相液、泡状流、弹状流、环状流、弥散滴状流、单相气6个区域。对于不同的本构模型,虽然流型转换相同,但流型转换位置的空泡份额不同。在壁面摩擦阻力中:αBS=αSA=0.8,αAM=0.9;在交界面阻力中:αBS=0.3,αSA=0.8,αAM=0.95;在交界面传热中:αBS=0.3,αSA=0.5,αAM=0.75。为避免数值求解困难,在程序计算中规定:α≤1.0×10-4为单相液;α≥0.99为单相气。
2) 壁面/相间质量和能量传递
(1) 壁面/相间质量传递
质量传递包括壁面沸腾产生的质量传递和相间蒸发/冷凝产生的质量传递两部分:
Γg=Γw+Γig
(8)
壁面沸腾产生的质量传递为:
(9)
式中:hcr为临界焓;εp为系数函数;hl为液相焓;hl,sat为液相饱和焓;q″w为壁面热流密度;aw为传热面密度;hfg为汽化潜热。
(10)
式中,ρf为液相密度。
蒸发/冷凝产生的质量传递为:
(11)
式中,Hil为液相和交界面的体积传热系数。
(2) 壁面/相间能量传递
流动沸腾条件下,考虑将壁面的热流密度分为气相和液相两部分,在五方程模型中气相假定为饱和态,因此壁面的热量全部用于提高液相的温度,故壁面处能量传递为:
Qwl=q″waw
(12)
传热面密度在流动面积不变的情况下可定义为:
无法,没破的不用管它,破了的只怕粘袜子,易非想找个创可贴把那儿贴住,可惜翻箱倒柜找了半天,也没找到一块,只好用纸巾隔在那里,再小心穿好袜子。
(13)
交界面传热Qil由交界面局部传热和近壁面传热两部分组成:
Qil=Hil(Tsat-Tl)-Γw(h′g-h′l)
(14)
3) 壁面摩擦阻力
ZEBRA的壁面摩擦阻力模型来源于TRACE程序[3],壁面摩擦阻力Fwall为:
(15)
式中:fwall,k为与k相(k=l,g)相关联的壁面阻力系数;De为水力直径,取决于截面的形状;Cwall,k为k相的壁面阻力系数。
Cwall,k取决于当前流型(图2),ZEBRA分别计算了单相液阻力系数、泡状流与弹状流相结合区域的阻力系数、环状流与雾状流相结合区域的阻力系数[3]。
单相液阻力系数fwall,single为:
(16)
泡状流与弹状流相结合区域的阻力系数:
(17)
(18)
过渡区流型的阻力系数:
Cwall,liq=ωfBSCwall,liq,BS+(1-ωfBS)Cwall,liq,AM
(19)
式中:a、b分别为单相液阻力系数参数;CNB为泡、弹状流区域阻力参数;ffilm为环状流区域阻力系数;wfBS为泡、弹状流权重因子;Cwall,liq为液相壁面阻力系数;Dh为等效水力直径;下标BS表示泡状流和弹状流相结合的流型,liq表示液相,AM表示环雾状流区域。
4) 交界面阻力与传热系数
交界面动量交换包括交界面阻力与交界面相变动量交换。通过类比单相管内流动,可得到由于两相之间的相对运动而产生的交界面阻力Fint:
(20)
式中:fk,k′为由于相对运动k′相施加给k相的阻力系数;Ci为交界面的阻力系数;ur为两相之间的相对速度。
对于气相和液相的交界面阻力,显然有:
Fint,g=-Fint,l=Ciur|ur|
(21)
ZEBRA交界面阻力模型建立在3个主要的流型上,即泡状流、弹状流及环形雾状流[3]。在泡、弹状流区域:
(22)
泡状流区域:
(23)
弹状流区域:
(24)
过渡流区域:
(25)
环雾状流区域:
(26)

同理,交界面传热根据流型分别计算各区域的传热系数。
泡状流区域:
(27)
弹状流区域:
(hliA‴i)CS=(hliA‴i)DB+(hliA‴i)LB
(28)
过渡流区域:
(hliA‴i)=wfAM(hliA‴i)AM+
(1-wfAM)(hliA‴i)BS
(29)
环雾状流区域:
(hliA‴i)AM=(hliA‴i)film+(hliA‴i)drops
(30)
式中:hli为传热系数;k为导热系数;dDB为弥散气泡尺寸;Nu为努塞尔数;A‴为气泡交界面积;wfAM为环雾状流权重因子;下标LB表示大型气泡区域,film和drops分别代表环型液膜和夹带液滴。
5) 水/水蒸气的状态方程
ZEBRA的两相模块采用与RELAP7相同的物性计算方法,即加密气体状态(SGEOS)方程。值得一提的是,Metayer等[13]已验证了SGEOS方程的精确度。
采用SGEOS方程来进行物性计算会显著提高两相模块的收敛性。两相流体关于每一相的SGEOS方程[13]描述为:
(31)
h(T)=γcVT+q
(32)
g(p,T)=(γcV-q′)T-
(33)
cp=γcV
(34)
式中:T、h和g分别表示流体的温度、焓和Gibbs自由能;γ、q、q′和p∞为各相流体的特性;cV为比定容热容;cp为比定压热容。
水和水蒸气的相关参数列于表1。
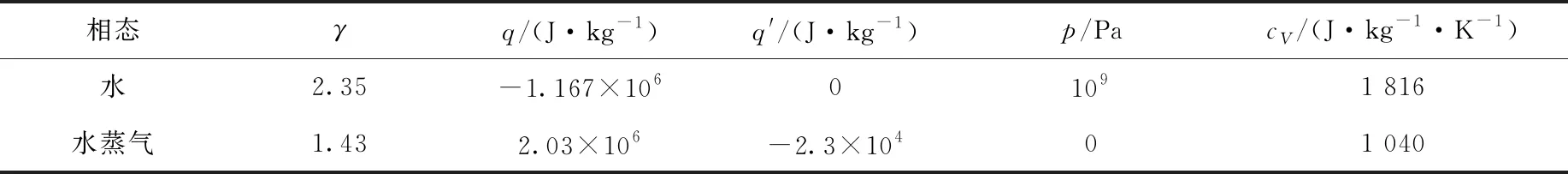
表1 水和水蒸气的相关参数Table 1 State parameter of water and its vapor
当前压力下的饱和温度计算[13]为:
(35)
式中,A、B、C和D为分别为饱和温度计算系数。
3 数值方法
ZEBRA基于MOOSE开发,采用有限元方法离散,本文以式(1)为例说明其数值离散过程。
3.1 空间离散
在MOOSE中对控制方程进行离散首先需要形成弱解形式,即形函数与控制方程内积的形式。
第1步,控制方程(式(1))左右两边同乘形函数:
(36)
第2步,在求解区域积分:
(37)
以内积形式表示为:
(38)
第3步,划分积分区域:
(39)
式中:Ω为总积分区域;e为子单元;ψ为有限元形函数;Ωe为积分子区域;wq为每个积分点q处的权函数;Je为子区域映射雅克比矩阵;i为各积分点的编号。
将式(39)应用在各节点上,可得到液相质量守恒方程在各积分区域的各节点上的离散方程组。
MOOSE支持一阶(1维EDGE/2维QUAD4)和二阶单元类型(1维EDGE3/2维QUAD9)等多种单元类型。对于一阶/二阶类型,形函数可采用线性/二阶拉格朗日函数。
ZEBRA在对空间离散时支持二阶精度。
3.2 时间离散
时间项的有限元离散过程与空间项相同,即:
(40)
MOOSE支持多种时间离散格式,包括显式欧拉、隐式欧拉、Crank-Nicolson、二阶时间离散格式(BDF2)和Implicit-midpoint等。以式(40)中的导数项为例,采用BDF2离散时:
(41)
式中,n为当前时间步长。
ZEBRA在对时间离散时支持二阶精度。
4 数值验证与计算分析
本文选取Bartolomei过冷沸腾实验[14]对ZEBRA两相流模块进行了初步验证。Bartolomei实验中实验段为垂直圆管,其管径为12 mm、管长为1.5 m、管厚为2 mm,管壁以均匀热流进行加热。表2列出该实验的一系列实验工况,压力范围为3.01~14.79 MPa,质量流密度范围为405~2 123 kg·m-2·s-1,管壁热流密度为0.42~2.21 MW·m-2。该实验的空泡份额绝对误差范围为±0.04。实验测量值只给出了空泡份额随平衡态含气率的变化,因此本文也只对比了空泡份额沿平衡态含气率的分布情况,其中平衡态含气率xq为:

表2 Bartolomei圆管过冷沸腾实验工况[14]Table 2 Experimental condition of Bartolomei flow boiling test[14]
(42)

本文评估了ZEBRA忽略气相能量守恒方程对计算结果的影响,以及二阶精度与一阶精度之间的差距,选取case1进行了对比计算。本文采用30个轴向节点进行计算,计算结果如图3所示。由图3可看出,ZEBRA二阶精度计算结果与实验值符合更好,ZEBRA一阶精度计算值与RELAP5计算结果相近,在较低平衡态含气率处(≤0.0)有一定偏差,在较高平衡态含气率处(≥0.0)相对误差在20%之内。

图3 不同计算精度下ZEBRA、RELAP5结果与实验值的对比Fig.3 Comparison of ZEBRA and RELAP5 results and experimental value with different calculation accuracies
采用二阶离散格式计算case1工况,其网格无关性验证如图4所示。由图4可看出,随轴向节点数的增加,轴向出口空泡份额在0.506附近震荡,且震荡逐渐减小,趋近于0.506。因此本文选取170个轴向节点作为计算节点个数。
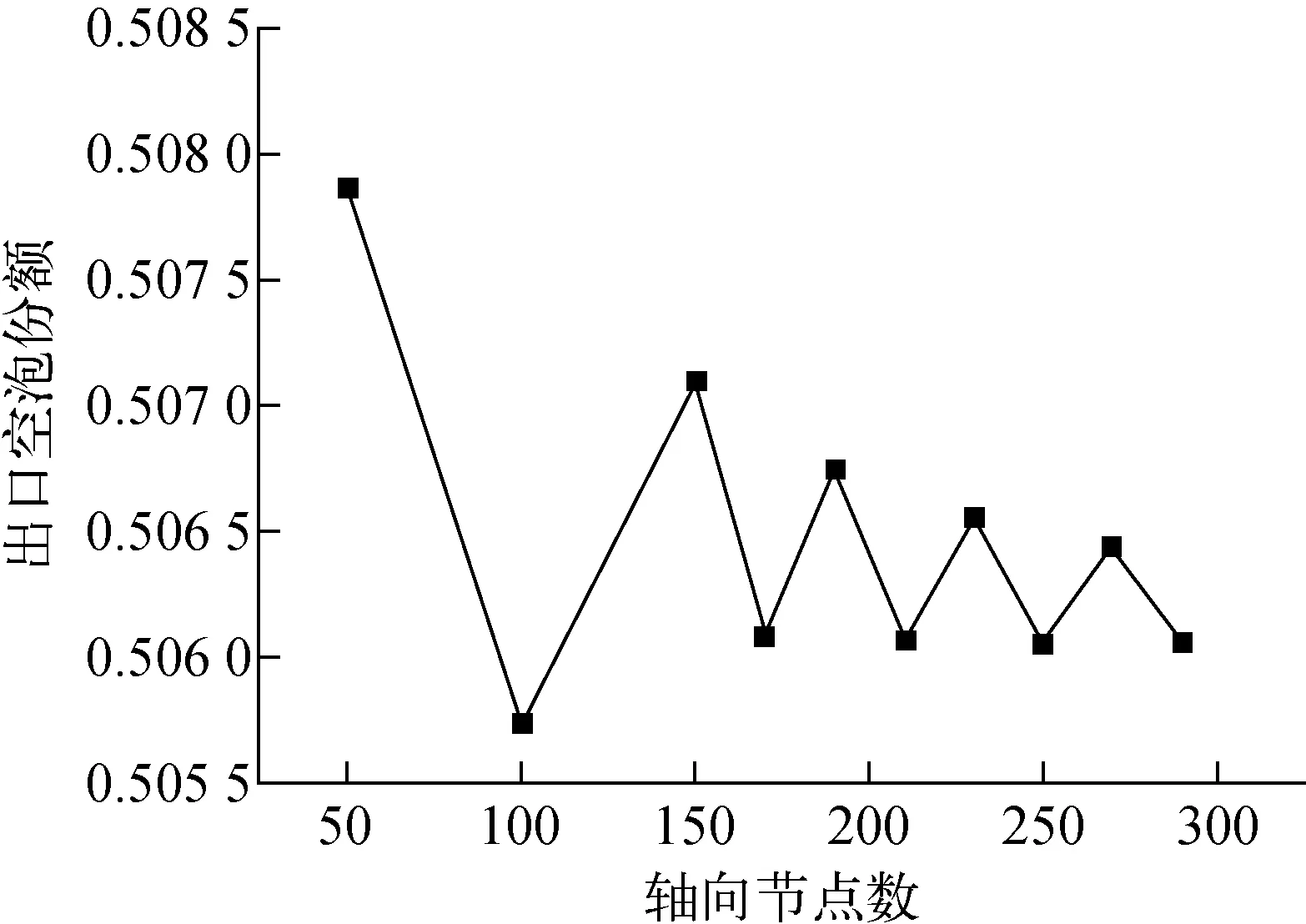
图4 轴向出口处空泡份额网格无关性验证Fig.4 Verification of grid independence in outlet void fraction
采用50个时间步对各工况进行计算,验证ZEBRA计算是否能达到稳态,如图5所示。由图5可看出,50个时间步足够达到稳态收敛条件,因此选取计算时间步为50。
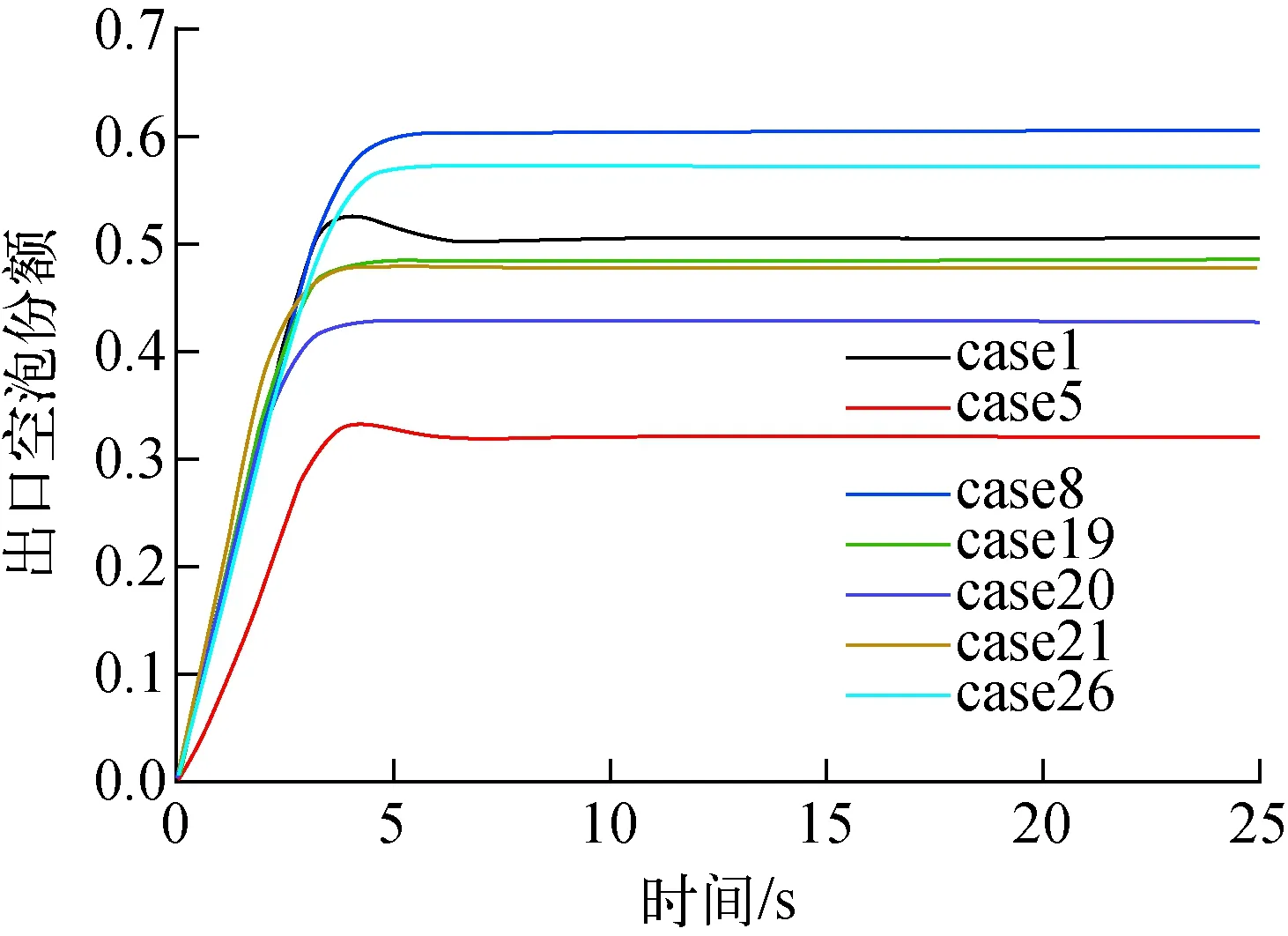
图5 出口空泡份额收敛性验证Fig.5 Convergence verification in outlet void fraction
计算过程中,沿单管轴向划分170个节点,网格单元类型为EDGE3,所有待求解变量U=[p,α,ul,ug,Tl]T在空间上均采用二阶有限元离散格式。采用伪瞬态求解,时间离散采用BDF2格式,计算时间步长为1 s,计算时间步为50。
为实现不同压力、质量流密度、壁面热流密度下的程序验证,本文只选取Bartolomei实验中若干组典型工况进行对比(表2),空泡份额与实验值对比如图6所示。图6中:不同热流密度下对比选取case1、case5、case8;不同质量流密度下对比选取case19、case20、case21;不同压力下对比选取case1、case19、case26。将ZEBRA预测结果与实验结果的误差进行计算,如图7所示。

a——不同热流密度;b——不同质量流密度;c——不同压力图6 空泡份额计算结果与实验值对比Fig.6 Void fraction comparison between calculated value and experimental value
由图6a与图7可看出,在中压(约7.0 MPa)、低质量流密度(约1 000 kg·m-2·s-1)的条件下,ZEBRA在平衡态含气率为正值区域(≥0.0)计算值与实验值符合良好,最大相对误差小于20%,随热流密度的增加(0.44~1.7 MW·m-2),空泡份额最大值由0.3增至0.6,且沸腾起始点逐渐提前。
由图6b与图7可看出,在较高压力(10.81 MPa)、中等热流密度(约1.13 MW·m-2)条件下,质量流密度越高,ZEBRA计算值与实验值符合越好,空泡份额最大值均为0.45左右。误差主要集中在平衡态含气率为负值区域,相对误差约为60%,平衡态含气率为正值区域与实验值均符合良好。
由图6c与图7可看出,在低质量流密度(约1 000 kg·m-2·s-1)、中等热流密度(约1.13 MW·m-2)条件下,压力越低ZEBRA计算值与实验值符合越好。随压力的增高,空泡份额随平衡态含气率的斜率逐渐减小,且沸腾起始点逐渐前移。

图7 ZEBRA计算值与实验值的误差Fig.7 Error of ZEBRA calculated value and experimental value
综合图6、7可得出:ZEBRA计算值与RELAP5计算值相近,在低空泡份额区域RELAP5计算值更接近实验值,其原因是RELAP5考虑了相间能量传递,在高空泡份额区域ZEBRA计算值与RELAP5基本相同;在平衡态含气率为正值区域(≥0.0),ZEBRA计算值与实验值均符合良好(最大相对误差小于20%),随热流密度的增加、质量流密度的减小、压力的增加均能使沸腾起始点向前移动。
ZEBRA计算值在低质量流密度、高压状态下的平衡态含气率为负值区域与实验值有一定差距(相对误差约为80%),其主要原因为:1) 在沸腾时起始点处,实验中贴近壁面处的流体温度高于饱和温度便可产生气泡,而ZEBRA采用一维模型进行计算,无法计算三维效应,因此导致程序计算的沸腾起始点滞后于实验值;2) 在低质量流密度下,主流对壁面气泡产生扰动较小,更易产生气泡,因此更易测得空泡份额,而本文程序计算模型无法精确模拟此过程,因而计算出的空泡份额较小;3) 在实验中,由于参数的测量误差、仪器的精度和两相问题的不确定性等问题,导致计算值在低空泡份额处与实验值有一定差距。
5 结论
本文基于MOOSE框架开发了五方程两相流程序ZEBRA,实现了二阶有限元空间离散格式和BDF2时间离散格式的两相问题求解。采用Bartolomei单管过冷沸腾实验中的部分实验工况对程序进行了初步验证,分别在不同热流密度、质量流量、压力下将程序计算值与实验值进行对比,结果如下。
1) 针对Bartolomei实验,ZEBRA采用五方程模型计算结果与实验值在平衡态含气率为正值区域(≥0.0)符合良好,相对误差小于20%,在平衡态含气率为负值区域(≤0.0)有一定误差。因此ZEBRA可较好地预测平衡态含气率为正值(空泡份额≥0.2)区域的单管两相流动传热问题。
2) ZEBRA在低流量、低压、高热流密度情况下与实验值有一定误差,其原因在于ZEBRA是一维程序无法精确计算局部气泡的产生过程,且五方程模型忽略了由液相到气相的能量传递过程,具有一定局限性。

