随机机会约束的多式联运多目标优化

尹传忠，方颢蓉，武中凯，郑士源

(1.上海海事大学 交通运输学院，上海201306；2.中国铁路哈尔滨局集团有限公司 经营开发部，黑龙江 哈尔滨150006；3.大连交通大学 机械工程学院，辽宁 大连116028)

通常意义上的多式联运优化研究是在不同情景下构建模型，通过某些算法得到最优运输方案。运输方案一般包括运输路径和运输方式选择，多假设问题所处的环境是确定的。ZILIASKOPOU‐LOS等[1]以运输时间最短为目标建立了多式联运最短路选择模型。李玉民等[2]综合考虑时间、费用和碳排放因素构建多目标优化模型，并根据客户差异化需求加权求和，将模型转化为单目标问题求解。HAO等[3]建立了限制交付时间的最小化广义运输成本的多式联运动态规划模型。MOCCIA等[4]认为联运过程中预定运输服务具有固定的时间窗口，研究带时间窗的多式联运组织优化。此类研究多为单目标模型，或将多目标问题转化为单目标求解，在时间约束方面多考虑交付时间限制，或将各节点进行单一的时间窗设置。此外，一些文献围绕不确定规划理论对多式联运问题展开研究，HOFF等[5]设计了随机需求下的多式联运网络。王清斌等[6]认为中间节点转运作业时间具有随机特征。DEMIR等[7]建立包含随机运输时间和需求的多式联运服务网络，运用样本均值近似方法求解并用实例证明了考虑随机性在提高运输计划可靠性上的优势。目前，关于随机规划的求解方法主要包括2类：一是将其转化为确定性形式求解，该方法适用于一些较为简单的特殊情景。二是逼近法，即通过模拟仿真生成大量样本数据集来逼近函数，并结合智能算法求解，该方法研究较少，但算法普适性较高，可使用范围更广泛，当模型进一步丰富完善时该算法仍然可行。本文建立考虑班期的随机多式联运多目标优化模型，该模型以总期望成本与总期望时间为优化目标，对铁路与水路运输设置班期限制，同时考虑在途时间和换装时间的随机性,引入货物在时间窗内交付的准时率，以直观反映运输服务水平。设计一种结合随机模拟技术和改进的自适应NSGA-II的混合启发式算法(MO-ANSGA-II)求解。

1 问题描述

考虑到铁路与水路具有固定的运输时刻表，公路运输较为灵活，中间节点的时间限制根据转运情况不同有所区别。当转运至公路运输时，无时间约束；当转运至铁路/水路运输时，该节点受班次限制，设置硬时间窗约束。如图1，T1，T2，T3是某节点铁路/水路的固定班次，货物到达该节点后换装至铁路/水路，进行下一阶段运输时会出现3种情景：在t1时刻到该节点，班次T1恰好发出，需要先完成换装，等待班次T2发往下一个节点；在t2时刻到达节点，完成换装后等待T2班次；在t3时刻到达节点，在换装过程中班次T2发出，需要等待班次T3发往下个节点。

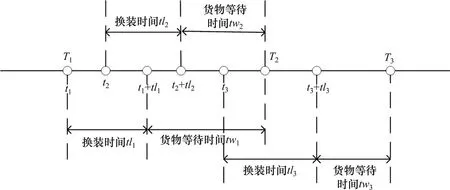
图1 铁路/水路班次运行示意图Fig.1 Railway/waterway transportation schedule

2 优化模型

2.1 模型假设

1)货物在运输过程中不进行拆分且仅在节点处进行转运；

2)同种运输方式的运输速度和单位成本在不同路段均相同；

3)3种运输方式的在途时间及换装时间是随机变量且均服从正态分布[6,8-10]。

2.2 符号说明

模型中的参数与变量说明见表1。

表1 模型参数与变量Table 1 Parameters and variables

2.3 模型构建

基于标准机会约束规划[11]，构建基于随机机会约束的多式联运多目标优化模型。

目标函数：

其中：

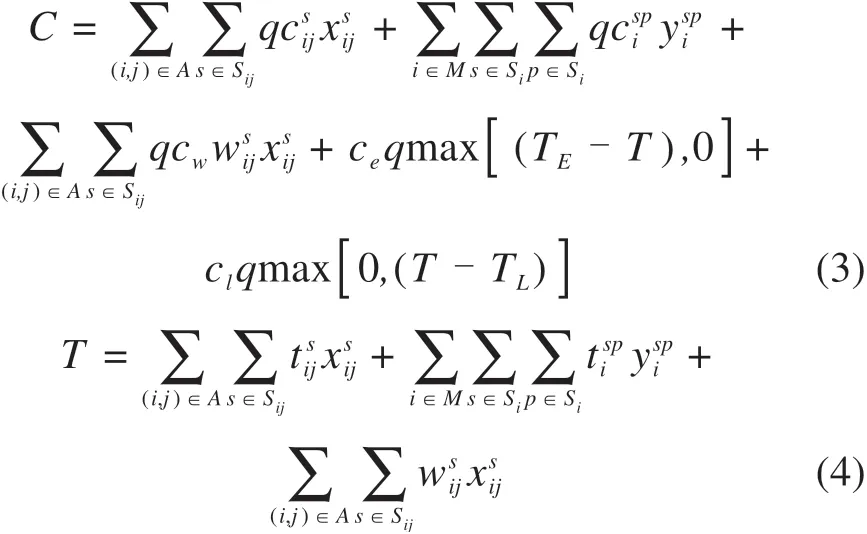
式(1)表示总的期望成本最小；式(2)为总期望时间最小；式(3)指总期望成本包括在途运输成本、换装成本、中转节点等待班次产生的等待费以及在目的地节点因过早/过迟交付货物产生的等待费/惩罚费；式(4)指货物从起点到终点所花费的总时间，包括在途时间、换装时间、中转节点等待班次的时间。

约束条件：

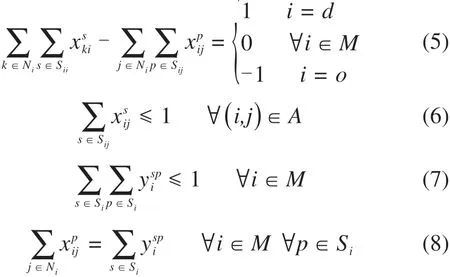
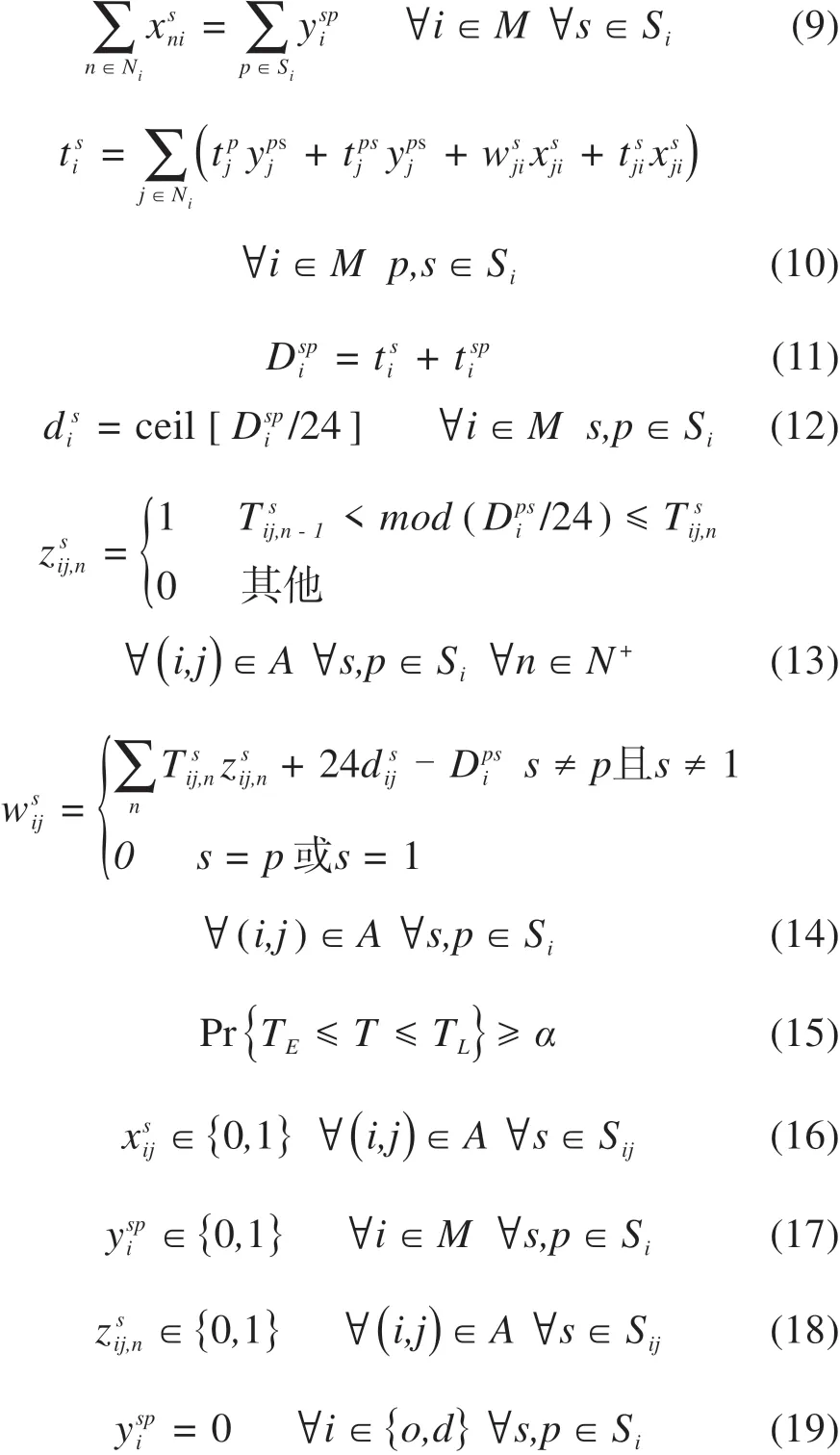
式(5)保证节点货流平衡；式(6)使货物在2节点间仅选择一种运输方式；式(7)表示货物在节点换装次数至多一次；式(8)与(9)保证运输过程中货流不可拆分；式(10)为货物从起点O由运输方式s到达节点i的总时间；式(11)为货物从起点到达节点i且完成运输方式s转换为运输方式p的总时间；式(12)为运输方式s到达节点i经历的天数；式(13)确定货物从节点i到j是否选择运输方式s的第n班车；式(14)为货物在节点i等待运输方式s出发所产生的等待时间，当不发生转运或转为公路时值为0；式(15)为机会约束，在规定时间内交付货物的概率不小于α，可将此概率称为准时率，准时率越高，满足在客户要求的时间窗内交付的概率越大，直观地反映方案运输服务水平高低；式(16)～(18)为0-1变量；式(19)表示在起点与终点无转运过程。

3 算法设计

模型中的目标函数与约束条件中均有随机变量，可利用随机模拟技术处理。此外，多式联运多目标优化模型属于NP-hard[12]问题，可使用智能算法求解,其中NSGA-II是权衡各子目标获得Pareto解常用智能算法。因此设计一种改进的自适应NS‐GA-II与Monte Carlo模拟结合的混合算法(MOANSGA-II)。

3.1 Monte Carlo模拟

3.2 改进的自适应NSGA-II

3.2.1 染色体编码与解码

染色体采用混合编码的方法，分为2个区域，前一部分代表网络中的节点，长度为节点数，由0和1组成，1代表通过节点反之取0。头尾部基因固定为1，代表起点与终点；后一部分代表2节点间的运输方式，长度比前一部分小1。对染色体进行解码时，后一区域的有效长度为L(L为前一区域1的数目)，无效区域不参与解码。

3.2.2 种群初始化

多式联运网络往往是非完全连通的，随机生成的初始解存在大量非可行解，影响算法寻优效率。使用深度优先搜索(DFS)得到所有连通的路径集合，从该集合中随机选择满足机会约束的个体作为初始种群，以避免非可行解的影响，提高算法效率。

3.2.3 改进的自适应拥挤距离选择算子

传统的拥挤距离Di是通过计算与其相邻的2个体在各子目标上的距离差之和获得。简单淘汰拥挤距离小的个体，可能会导致某些个体间距离差距过大，此外2个相邻个体在不同子目标上距离差异程度较大的个体无法获得更多遗传机会，这会影响种群分布多样性。本文在个体选择过程中进行自适应调整，避免了种群分布出现距离差距过大的情况。个体i的新拥挤距离D′i的计算公式[13]：

其中，表示个体i在各个子目标上与其相邻个体的拥挤距离的方差，Vi=是非支配排序后个体i相邻2个体的第k个子目标的函数值。新的拥挤度算子考虑到各个子目标拥挤度距离的差异程度，有利于保持种群分布的多样性。

3.2.4 自适应交叉与变异

一般的NSGA-II交叉、变异概率是人为设置的固定值的，无明确的设置规则。本文考虑使用自适应策略调整概率，通过改变交叉变异的概率以期望跳出局部最优[14]，自适应调整按如下公式：

其中，P(i)是第i代进行交叉/变异的概率；ki为当前代数与最大进化代数之比；maxP，minP为预设的交叉/变异概率的上下限。

3.3 MO-ANSGA-II算法整体流程

算法的具体流程如图2所示。

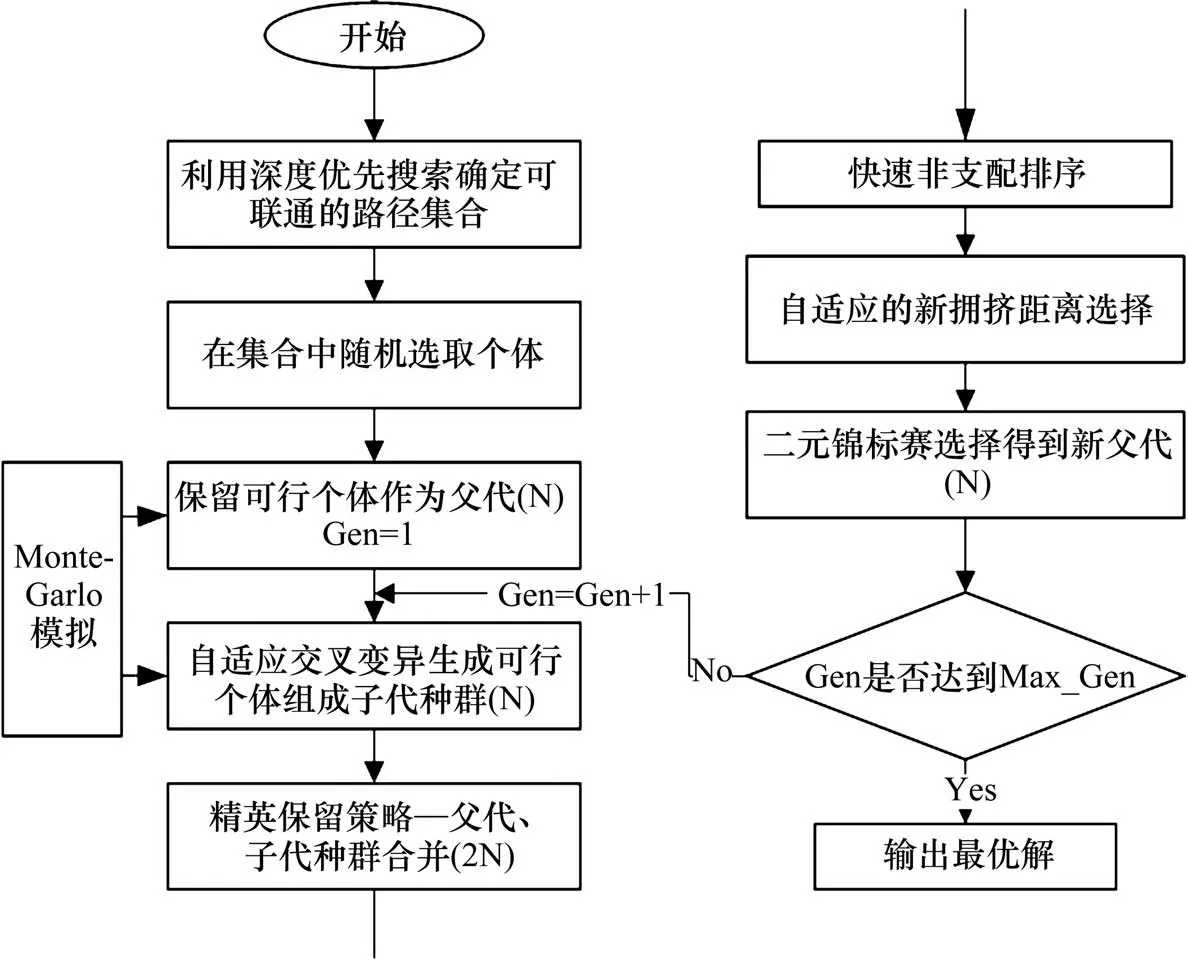
图2 MO-NSGA-II算法流程Fig.2 Flow chart of MO-NSGA-II

4 算例分析

4.1 基础数据

随机生成一个有21个节点，37条运输弧，3种运输方式的多式联运网络。

假设有一批5 t的货物从节点0运往节点20，准备开始运输的时间为6点，托运人要求交付时间窗为(45 h，75 h)。设公路、铁路、水路运输的平均速度为70，60和30 km/h。

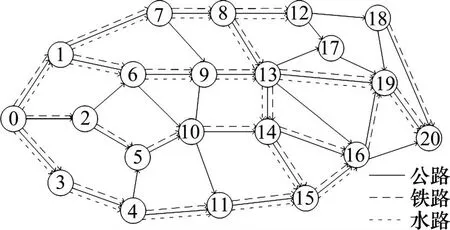
图3 多式联运运输网络图Fig.3 Multimodal transport network

假设各城市节点间的在途运输时间是随机的，服从正态分布，方差为1；节点间转运时间也是随机的，服从正态分布，具体如表2。

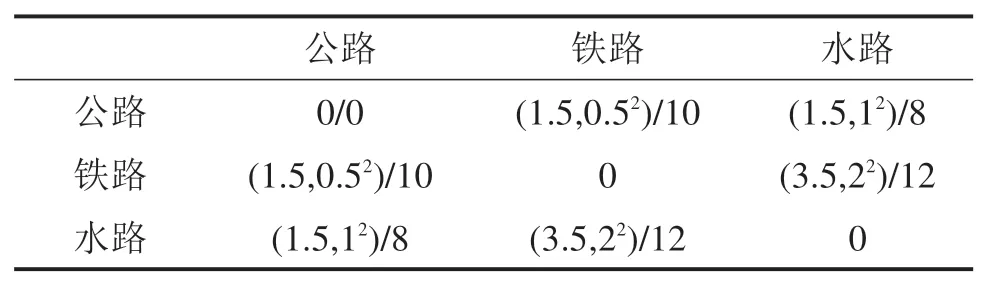
表2 各运输方式间的单位转运时间/成本Table 2 Transfer time/cost of the different transport modes(h∙元−1∙t−1)

公路、铁路、水路基于运输距离的单位运输成本分别为0.5，0.3和0.02元/(t∙km)，单位换装时间与成本如表2所示。货物提前/延迟交付产生的单位等待/惩罚成本为1.5/2.5元/(t∙h)；货物在中间节点等待出发产生的单位等待成本为0.5元/(t∙h)。

各城市节点间公路运输灵活，铁路运输、水路运输具有固定的运输班次，随机生成各城市节点间铁路与水路的每日固定发车/船班次时刻表。

4.2 结果分析

本算例随机模拟次数为500次，机会约束概率为α=0.6，初始种群为50，最大遗传代数为300，交叉概率为MaxPc=0.95，MinPm=0.55，变异概率为MaxPm=0.05，MinPm=0.005。

采用python3.7求解，计算得到的Pareto最优解如图4，每个点代表一种运输方案。具体的Pare‐to最优解如表3(保留3位小数)。

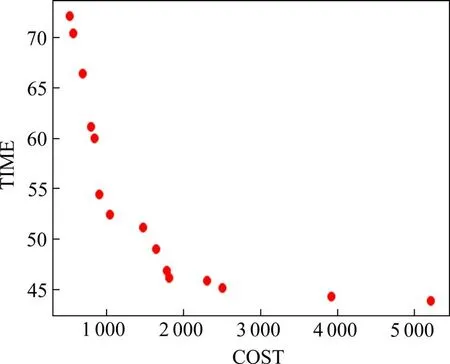
图4 Pareto最优解Fig.4 Pareto optimal solutions

表3 中，节点栏中数字代表经过节点的编号，运输方式栏中1，2和3分别代表公路、铁路、水路运输。各方案在满足准时率大于60%的同时对成本和时间2个目标进行权衡。方案的期望时间在规定的交付时间范围内或附近，越靠近时间窗界限的方案，准时率越低，尽管靠近时间窗的方案能更好地完成某一目标，但当客户对交付时间要求高时，这些方案存在劣势。决策者可根据客户偏好和当前条件选择出更合适的方案。

表3 最终运输方案集Table 3 Final transportation schemes

以方案中时间、成本、准时率某一项最优的方案1，8，15为例，对比是否随机、有无班期情况下各指标区别，见表4。

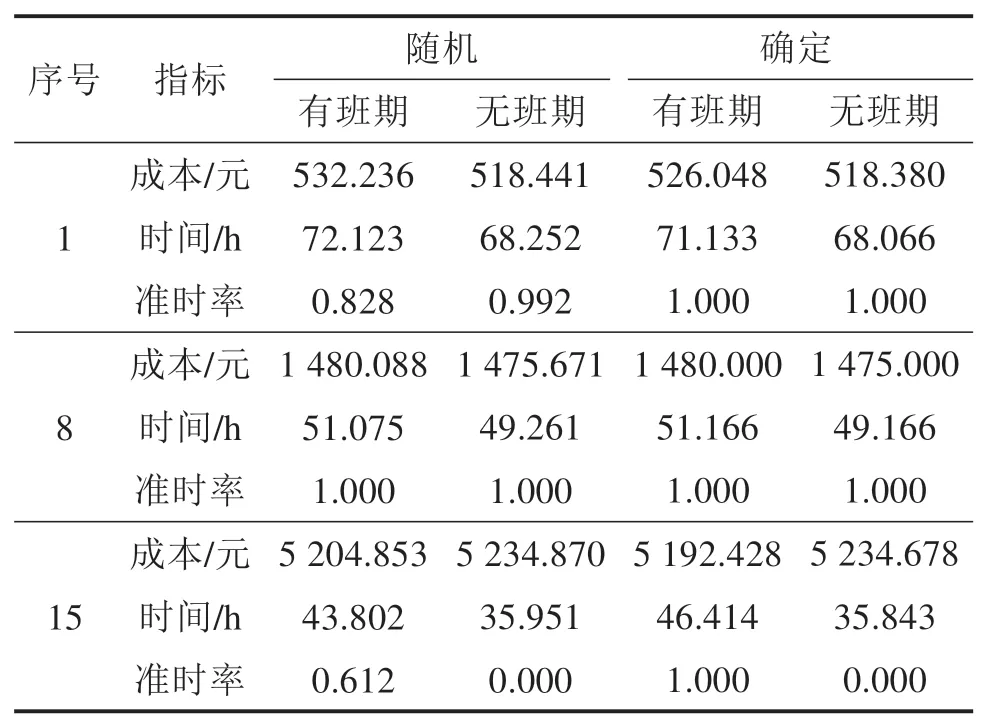
表4 不同情景下运输方案各指标对比Table 4 Indexes of transport schemes under different scenarios

1)随机情景下方案的准时率能够直观地将运输服务水平纳入方案指标。确定性情景下虽有准时率指标，但仅能取值1或0，因为确定性情景中，只存在可以在时间窗内交付和不能交付2种情况。确定、无班期条件下，方案15准时率为0，是指不可能在时间窗内交付，此方案将被淘汰。在随机、无班期情景下，方案15的准时率则是近似为0，表示“该方案在时间窗内交付”这一事件发生的概率极低，可近似视为不能在时间窗内交付。

2)采用单一运输方式的方案8，随机与确定性情景下成本、时间不同，但差异较小。

3)方案1和15在有班期、随机情景下的成本比有班期、确定情景下分别提高6.188元与12.425元。其主要原因是随机情况下可能出现时间窗外交付的情况，产生支付额外等待费/惩罚费，准时率越低发生概率越高。

4)有班期限制时，方案15在随机情景下的运输时间较确定情景下降低2.612 h。主要原因是该方案中货物到达公铁中转节点的时间靠近某一班次发车时间，确定性情况下会错过该班次而必须等待下一班次发出；而随机情况下存在提前到达节点，可以赶上此班次发出的可能，导致方案总时间下降。反之，当随机情况下出现错过某一班次而不得不等待下一班次发车的情况时，等待班次的时间增加，方案总时间也增加。也就是说有班期时，随机性可能会导致方案在中间节点出现提早发出或错过计划班次的情况，降低/增加等候班次时间，从而影响总时间。

5)相较于无班期，运输方案由于等待班期的情况出现，成本与时间均有明显提升。

总体上，是否考虑班期与随机因素均会导致运输方案的成本、时间、准时率发生变化，影响pareto最优解集选择。忽略班期和随机性不利于决策者制定符合实际的科学方案。

为了证明算法的有效性，对改进的自适应NS‐GA-II(ANSGA-II)与一般NSGA-II进行比较。两算法分别运行50次后，改进前后算法的平均解集数量、各目标最优值如表5所示。图5则显示了2种算法不同目标函数均值(去除重复个体)的收敛情况，其中改进后的算法在100代左右收敛，一般的NSGA-II算法在175代左右收敛。总的来说，ANS‐GA-II搜索到的解集数量更多，寻优能力更强，收敛速度更快，算法性能得到了有效提升。

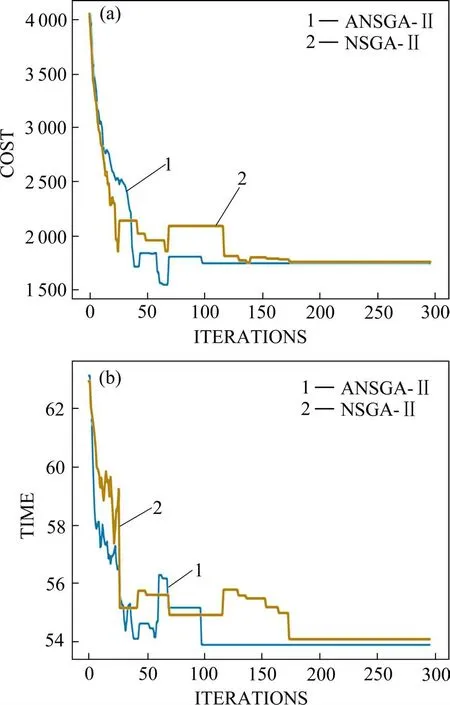
图5 不同算法下各目标函数均值收敛Fig.5 Iterative graph of the average value of each objective function under different algorithms

表5 算法结果对比Table 5 Comparison of algorithm results

5 结论

1)相比于确定情景，考虑随机情景的决策方案更能适应复杂的多式联运环境。

2)在不同情景下运输方案(是否随机、是否有班期)的成本/时间不同，具体变化程度因各方案的转运次数、班期、准时率等因素的不同而异。班期与随机性影响运输方案的成本、时间、准时率，从而改变得到的帕累托最优运输方案组构成。

3)基于不确定性理论，将一般的多式联运优化模型扩展为随机机会约束的多式联运多目标优化模型，反映在途与换装时间随机性，同时引入时间窗内交付货物的准点率作为机会约束概率，保证了运输服务水平。

4)MO-ANSGA-II用于求解随机机会约束的多式联运多目标优化模型，具有良好的运算性能。

面对复杂的多式联运运输过程，本文仍有进一步研究的空间，例如考虑多货流、客户需求等的不确定性，将绿色低碳纳入优化目标等都具有研究价值，此外，本文采用的算法性能也仍具有提升空间。