考虑初始应力各向异性弹塑性岩土体小孔扩张解

蒋功化，李超

(1.湖南路桥建设集团有限责任公司，湖南 长沙410004；2.中南大学 土木工程学院，湖南 长沙410075)

小孔扩张在土木工程中得到了广泛的应用，如桩基工程、注浆工程、地下工程和现场测试等。常采用不同的破坏准则和模型来研究和分析小孔扩张机理。岩土工程领域的一些小孔扩张分析如下：理 论 研 究[2−9,12,17,20−26,30,32−33]；工 程 应 用[10,13,31]；数值模拟与实验[11−19]以及其他。然而，上述发表的小孔扩张论文大多基于各向同性和不排水破坏准则，这与实践中的现场情况不符，由于土体的初始固结，天然土体初始应力可能是各向异性的[1,9]。另外，对于施工速度相对较缓慢的工程，尤其是对于渗透性高的岩土体，理论计算中采用排水假设，与实际工程中的现场情况更加相符。在饱和土体中，考虑初始应力各向异性和排水条件影响的理论解也很少。将基于K0-修正剑桥(K0-MCC)模型[9]应用于天然土体分析，提出了一种实用的近似闭合解，文中采用K0系数反映了初始应力各向异性的影响。CHEN等[4]在考虑排水条件的修正剑桥(MCC)模型的基础上，提出了圆柱小孔扩张问题的精确弹塑性理论解。RUSSELL等[14]提出了基于Mohr-Coulomb破坏准则的小孔扩张问题的相似解，以研究和分析砂土的行为。李林等[34−35]对初始应力各向异性黏土小孔扩张问题，基于临界状态模型，进行了详细的不排水解分析，并结合静压桩工程进行应用分析。同时，随着破坏准则和模型的发展，在更先进的土体模型(UST模型)中采用小孔扩张是必要的[28]。将统一强度破坏准则引入小孔扩张机理分析中，由于简单的数学表达式，在工程实践中得到了广泛的应用。综上所述，以上发表的小孔扩张论文大多是基于各向同性和不排水的破坏准则，对于施工速度相对较缓慢且渗透性高的岩土工程，理论计算可能产生较大误差。本文的主要目的是在统一强度破坏准则的基础上，考虑初始应力各向异性和排水条件的影响，针对施工速度相对较缓慢且渗透性高的岩土体问题，建立一个球孔扩张理论解。最后，通过发表的实例和参数研究来验证理论解的适用性，并用b系数反映了初始应力各向异性的影响。

1 问题描述

初始水平应力为σh0，初始竖向应力为σv0，随着内部扩张压力p的增大，小孔内壁首先出现屈服，随着内部扩张压力的增大孔壁周围岩土体逐渐发展成塑性区。小孔壁的最终半径为au，弹塑性边界半径为rb，相应的EP边界径向位移为urb，小孔扩张问题的示意图如图1所示。

图1 小孔扩张问题的示意图Fig.1 Mechanical model for cavity expansion

2 假设条件

一些假设表达如下：

1)YU[29]提出了统一强度理论(UST)，由于统一强度理论概念清晰，数学表达式简单，将统一强度理论应用于小孔扩张问题，数学表达式为：

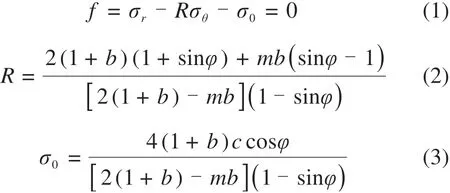
其中，黏聚力为c；内摩擦角为φ；b是反映中间主应力对材料屈服影响的强度参数(0≤b≤1)，m是中间主应力的参数；m→1意味着材料趋向于塑性状态，在下面的塑性分析中假设m≈1[28]。

2)在弹性区，应力−应变关系可以表示为：

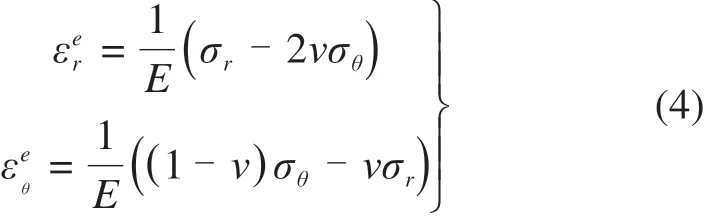
3)大应变理论的形式如下：

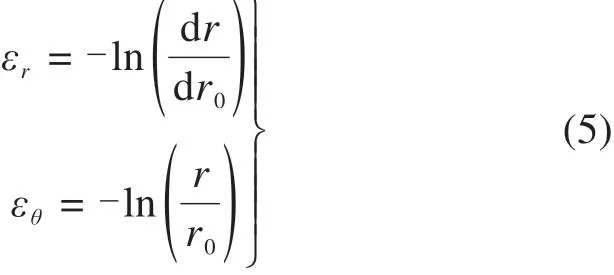
4)在弹性区和塑性区都满足应力平衡方程：

其中，σr和σθ分别是径向和切向应力。

5)平均应力p和偏应力q表示为：

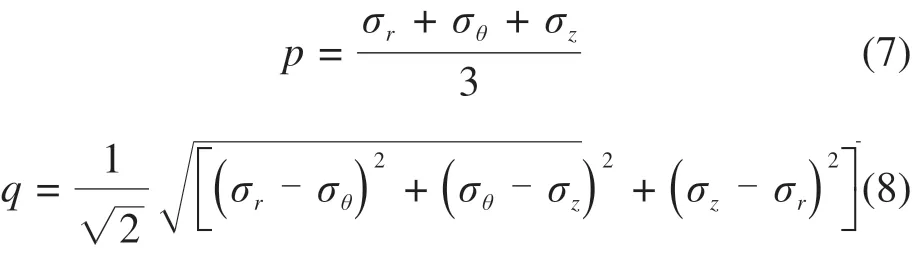
其中，σz是竖向应力。

3 理论推导

3.1 弹性区分析

弹性区土体的应力和位移可以写成：

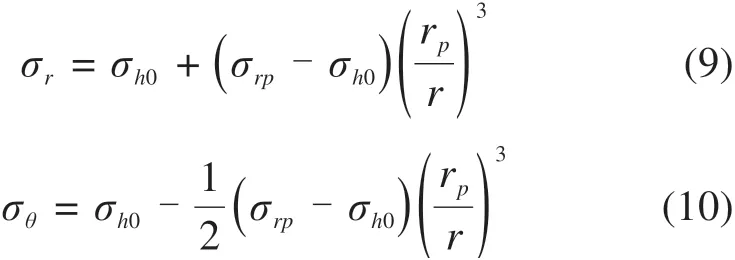
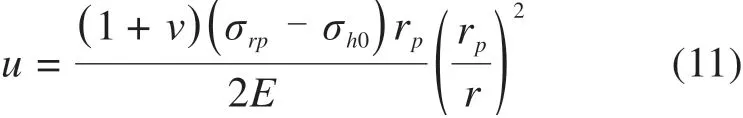
在EP边界，可以写出小孔周围土体的位移：

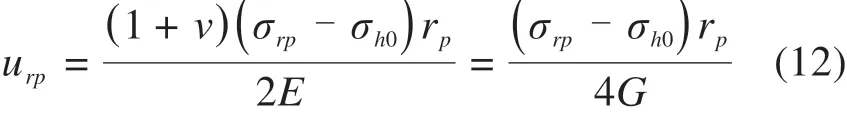
边界条件可以写出：

3.2 弹塑性边界分析

下面对弹性和塑性区的边界处进行分析。为了确定弹性和塑性区的位置(rb)，根据YU等[28]的相似解，计算排水条件下的半径(rb)。

根据YU等[28]的理论：

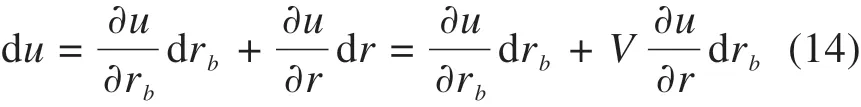
孔周土体颗粒的速度可以表示出来：

因此，

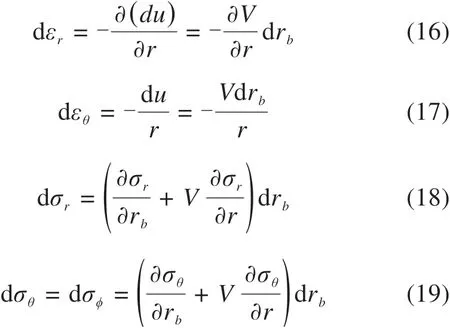
根据YU等[28]的观点，微分方程可以表示为以下形式，为了避免重复，没有对该微分方程进行详细描述。该微分方程的详细推导可参考文献[28]：

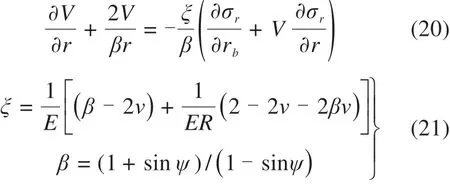
其中，ψ是剪胀角。

因此，

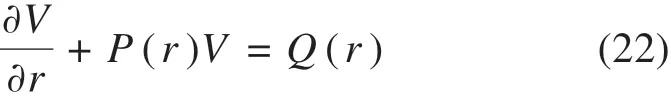
其中，

根据等式(11)，

由式(22)也可以得到：

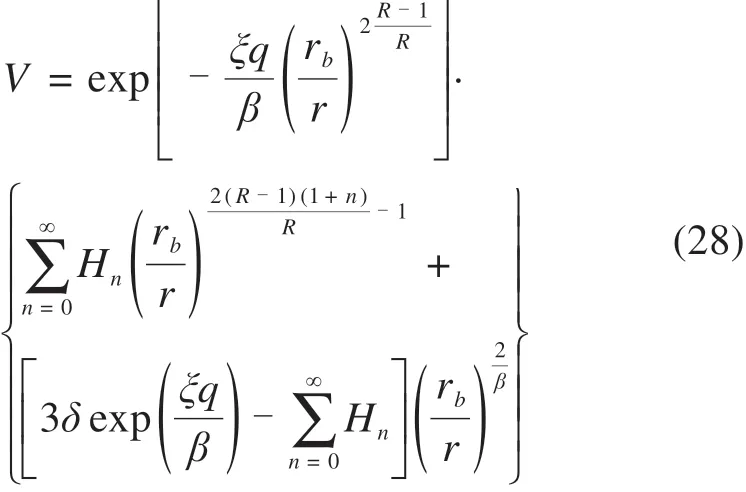
其中，

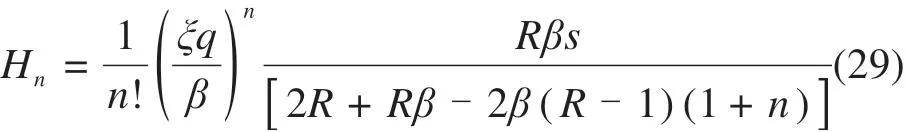
对于小孔壁r=a，V=da/drb，所以：

根据相似解技术可以表示：

半径(rb)与小孔壁当前半径(a)的比值可以表示如下：

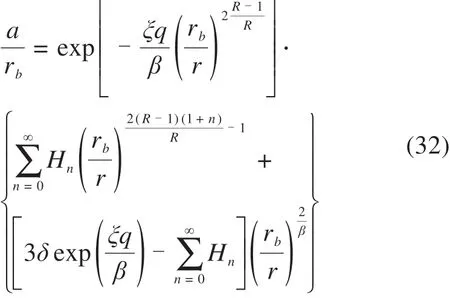
a确定后即可得到半径rb。

3.3 应力分析

下面对应力进行分析。联立等式(9)，(10)，(11)和(1)，也可以得到，也可以求出rb处的总径向应力：

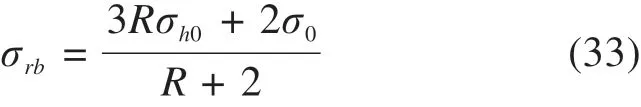
切向应力：

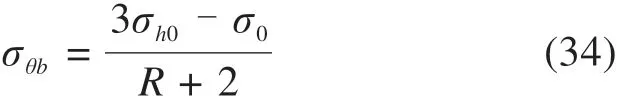
由于在塑性区岩土满足屈服准则和应力平衡方程，因此，将方程式(6)，(1)和边界条件联立可以得到：

联立式(35)，(33)和(13)：

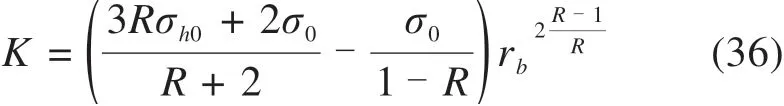
总径向应力可以得：

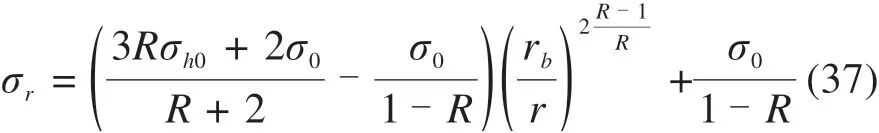
3.4 塑性区极限膨胀压力

根据式(35)可导出极限膨胀压力：

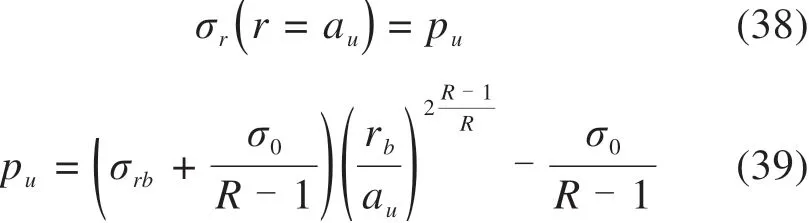
4 结果验证

土工材料的参数值参考YU等[27]，内摩擦角φ在20°～50°之间，剪胀角ψ在0°～φ°之间变化。如表1 所示，本解的结果(rb/a)与YU等[27]的数据基本一致。

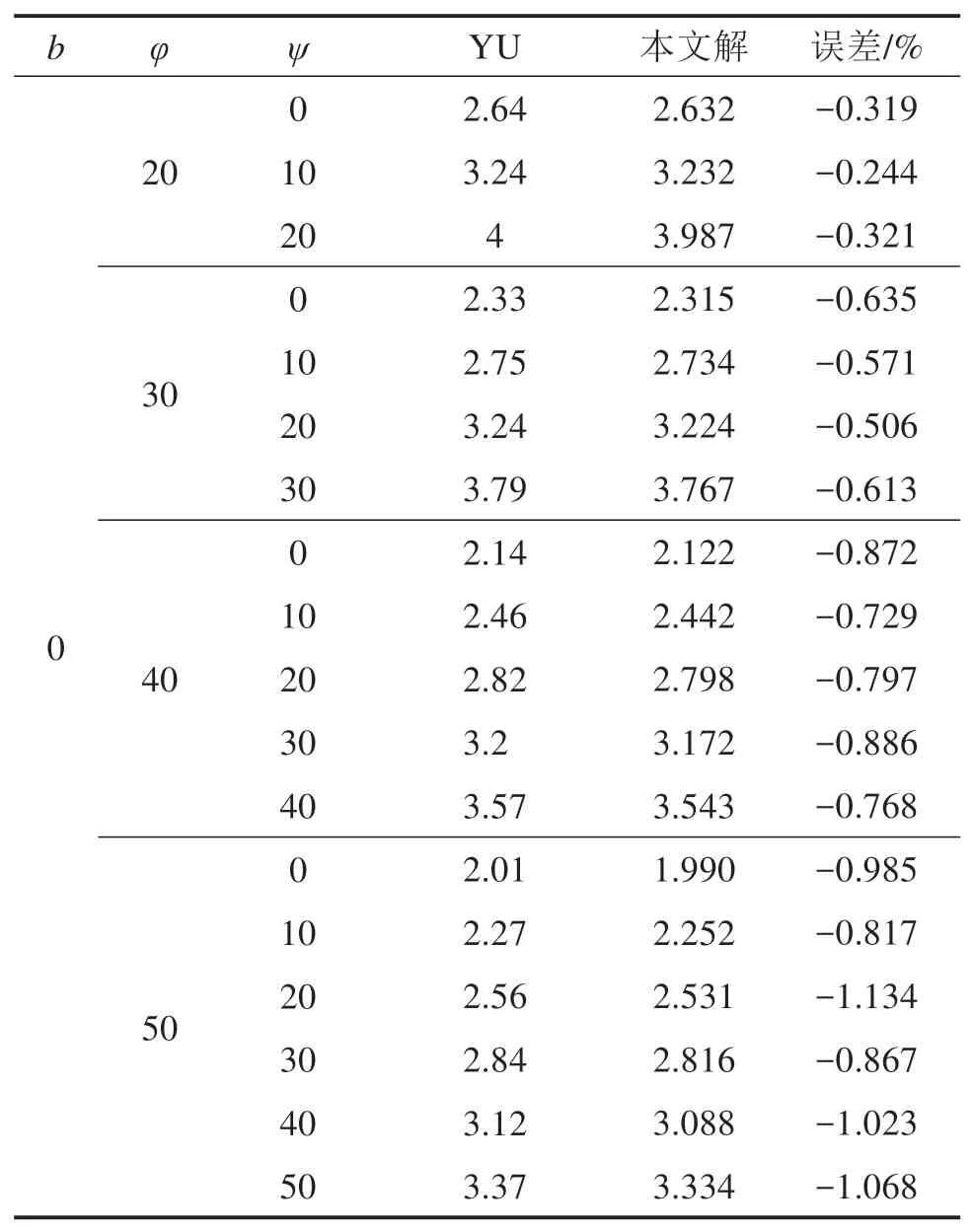
表1 本文解的结果(rb/a)与YU的比较Table 1 Comparison between the results(rb/a)of the present solution and YU

如图2和图3所示，研究了初始应力各向异性系数b对半径比和归一化内压的影响，半径比(rb/a)随初始应力各向异性系数b的增大而非线性减小，归一化内压(p/p0)随着初始应力各向异性系数b的增大，呈非线性增加，说明忽略初始应力各向异性系数b对半径比和归一化内压的影响会导致计算错误。

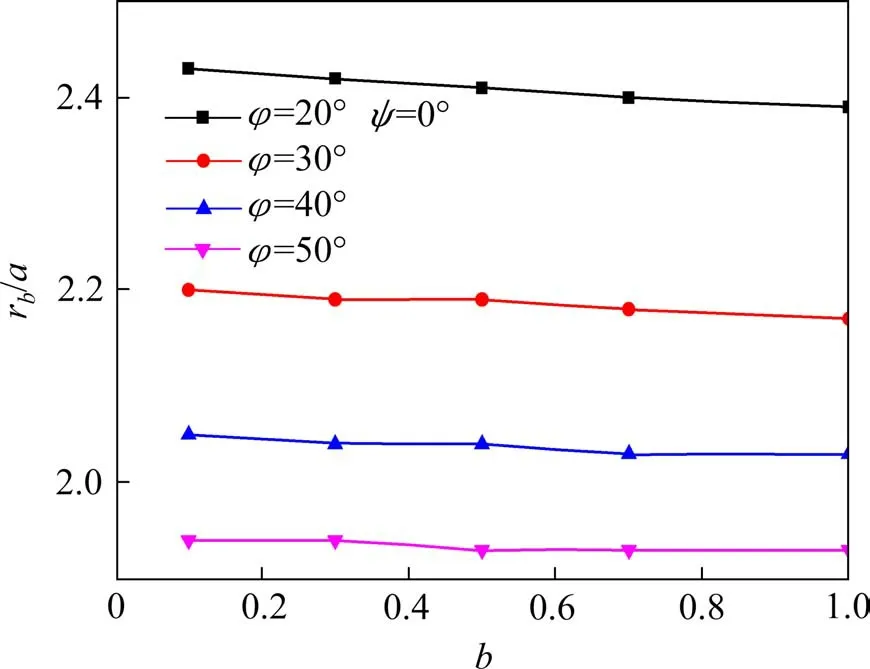
图2 初始应力各向异性系数b对rb/a影响Fig.2 Results(rb/a)of the present solution for different b

表2 本文解的结果(p/p0)与YU的比较Table 2 Comparison between the results(p/p0)of the present solution and Yu and Houlsby[27]

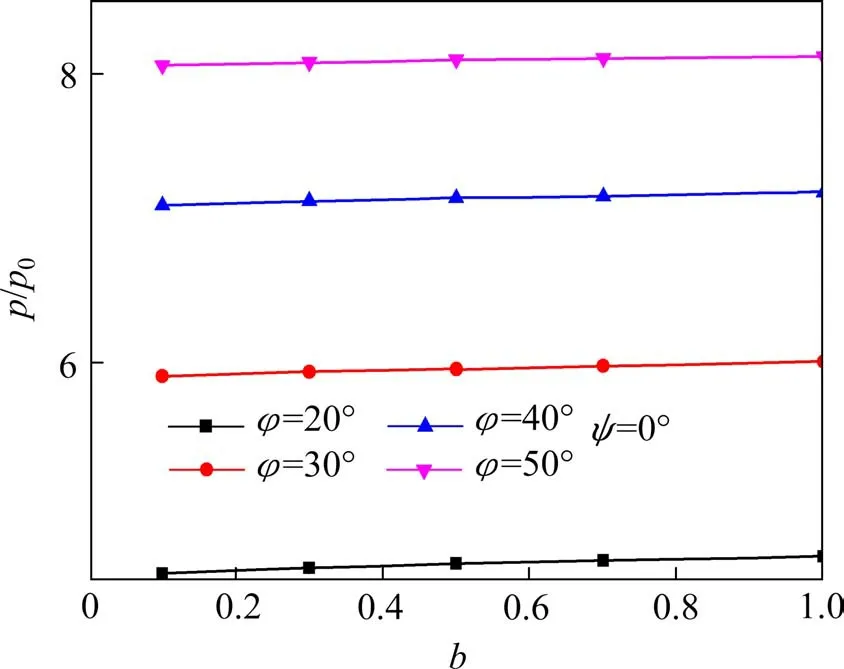
图3 初始应力各向异性系数b对p/p0影响Fig.3 Results(p/p0)of the present solution for different b

5 结论

1)与传统解不同，本文解同时考虑了岩土体各向异性和排水条件影响。

2)半径比(rb/a)随初始应力各向异性系数b的增大而非线性减小，归一化内压(p/p0)随初始应力各向异性系数b的增大而非线性增大。