钢轨波磨对车辆−轨道系统动力特性的影响

杨超，张玉龙，陈彪

(1.华东交通大学 机电与车辆工程学院，江西 南昌330013；2.中国铁道科学研究院集团有限公司 机车车辆研究所，北京100081)

铁路线路在投入运营一段时间以后，沿着钢轨表面的纵向往往会出现比较明显且具有一定周期的波浪形表面磨损，这种表面磨损称为波磨。研究发现在直线和大半径曲线的线路出现的钢轨波磨大部分为短波，其波长约为50～150 mm。小半径曲线线路出现的钢轨波磨一般为长波，其波长约为200～600 mm。当动车组以较高的速度在波磨区段运行时车辆走行部件及轨道系统剧烈振动，较大的钢轨垂向加速度容易造成弹性扣件松动，增加铁路养护维修费用[1]。另外，钢轨波磨也会造成车辆构架稳定性降低，波磨严重时会造成车辆转向架横向加速度超标报警，危害列车运行安全。众多国内外研究者致力于钢轨波磨机理和钢轨波磨对轨道-车辆动态响应规律等方面的研究。由于钢轨波磨原因复杂多样，目前有波磨现场测试、模拟钢轨波磨试验、仿真分析等方法研究钢轨波磨。GRASSIE[2]通过研究总结了钢轨波磨原因，并给出相应的缓解波磨的措施，同时还得出我国铁路线路的钢轨波磨大部分都与钢轨自身的固有频率相关。WANG等[3]通过改变波磨的波深和波长分析波磨对轮轨系统的影响，得出波磨对钢轨和轮对的振动有较大影响，对车体的振动影响较小。谷永磊等[4]研究了不同波深对轮轨相互作用力及车辆运行稳定性的影响，研究表明轮轨垂向力、轮重减载率和轮对振动加速度随钢轨波磨深度的增加而增大，导致车辆簧下部件的损坏；温泽峰[5]利用钢轨波磨计算模型分析了轨道缺陷与钢轨波磨之间的关系及影响。李伟等[6]通过对轮轨垂向耦合动力学和轮轨接触力学的研究提出了新的钢轨波磨计算模型。李霞[7]采用有限元法建立轮轨模型研究了钢轨波磨对轨道振型和共振频率的影响。针对地铁曲线线路钢轨波磨问题，宋小林等[8]对钢轨波磨进行现场测量并建立车辆-轨道模型，研究发现以波磨时变率作为参照对钢轨进行打磨较合理。本文通过多体动力学仿真软件UM创建车辆-轨道耦合动力学模型，仿真分析钢轨波磨对车辆构架振动特性，并结合现场试验数据研究高铁线路上某型动车组以不同速度级通过钢轨波磨区段时的轮轨接触动力学性能。

1 轮轨垂向耦合动力学模型及计算工况

1.1 车辆−轨道垂向耦合动力学模型

如图1所示，通过创建车辆-轨道垂向耦合动力学模型研究钢轨波磨对车辆-轨道动力特性的影响。把单节动车组看作以恒速在轨道上运动的多刚体系统，所建系统中包括车体以及前后转向架的沉浮和点头、4个轮对的垂向振动，轨道系统中钢轨不平顺为Z0i(t)。采用Spring力元模拟一系钢簧阻尼、抗蛇形阻尼器及横向阻尼器。车辆系统用弹簧和阻尼表示转向架与车体和轮对与转向架之间的关联方式，用连续的弹性离散点支承上的TIMOSHENKO梁模型模拟钢轨模型[9−11]，考虑高速铁路钢轨波磨的短波长特性，轨道以直线形式建模，钢轨长度为75 m，考虑扣件及橡胶垫提供的与动态行为相关的刚度和阻尼作为轨道垂向边界约束，图1中建立连续分布的单层轨道模型并利用Hertz非线性接触模型模拟轮轨垂向接触耦合关系。

图1 车辆−轨道垂向耦合动力学模型Fig.1 Vertically coupled dynamic model of train-track

车辆系统垂向运动方程表达式为：

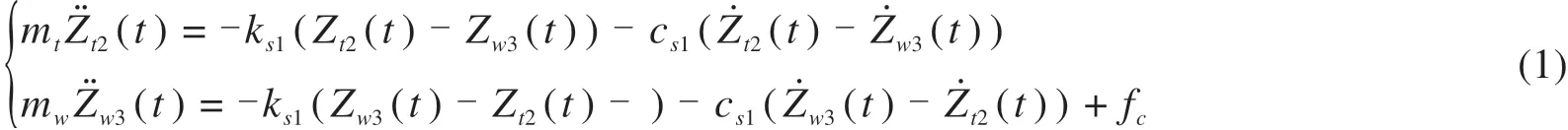
式中：mt，mw分别为一系弹簧簧上质量和簧下质量；Zt2(t)，Zw3(t)分别为车体和轮对的垂向位移；ks1，cs1分别是一系悬挂的等效刚度和阻尼。

轮轨垂向接触力表达式为：

式中：CH为赫兹接触常数，取93.7 GN/m3/2；r为波磨产生轮轨间相对位移激励；Zw(t)，Zr(x,t)分别是车轮和钢轨的位移。

1.2 计算工况及模型参数

根据车辆参数和轨道参数，利用UM多体动力学仿真软件创建车辆-轨道模型，车轮踏面采用LM型磨耗型踏面，轨道采用60 kg钢轨型面，线路轨底坡设定为1:40，并将试验区段实测的钢轨波磨数据以轨道激励的方式输入到模型中。高速动车组以不同速度级匀速通过波磨区段作为计算工况，分析动车组通过波磨区段时的轮轨接触动力学性能。

表1 车辆参数Table 1 Vehicle parameters

2 仿真结果分析

2.1 波磨对车辆横向稳定性影响

根据试验区段钢轨的波磨深度不同将实测波磨深度最小区段定义为1阶波磨，在实测波磨波形基础上乘以系数α(α=λi/λ，其中λi为不同波磨波深幅值，λ为实测波深幅值，α取1，2，3和4)模拟不同波深的波磨，依次得出2阶、3阶和4阶波磨。以260～350 km/h的速度区间作为计算工况，动车组以不同的速度级通过上述不同波深的波磨路段时对应的构架横向加速度和轮轨横向力如图3和图4所示。

图3 不同波磨对应的构架横向加速度Fig.3 Transverse acceleration of frame corresponding to different rail corrugation

图4 不同波磨对应的轮轴横向力Fig.4 Transverse force of wheel shaft corresponding to different rail corrugation

图3 中构架的横向加速度随着动车组运行速度的增加而增大，速度一定时波深越大构架横向加速度和轮轨横向力均越大，当动车组通过波磨区段的速度小于300 km/h时对应1阶、2阶、3阶波磨的构架横向加速度和轮轴横向力差值较小。当车速大于300 km/h时，4阶波磨对应的构架横向加速度及轮轴横向力的值变化速度最快，各阶波磨对应的构架横向加速度值和轮轴横向力之间的差值逐渐增大。图4中当车速大于285 km/h时，2阶波磨下轮轴横向力大于3阶波磨的轮轴横向力。

这里引入波深对时间的1阶导数为波深时变率，图5为高速动车组以300 km/h的速度级通过波磨程度不同的波磨区段构架横向加速度曲线，图6为构架横向加速度在不同波深的波深时变率下的功率谱密度图。

由图5可知，1阶和2阶波深的波深时变率对应的车辆构架横向加速度最大值约为6.1 m/s2和8.1 m/s2；3阶和4阶波深的波深时变率对应的构架横向加速度最大值约为11.6 m/s2和13 m/s2。因此，较大波深的波深时变率可能会造成构架横向加速度超出允许范围，进而造成车体晃动影响列车的正常行驶[12]。图6中可以看出，不同波深的波深时变率对应的构架横向加速度功率谱密度主要集中在5～6.5 Hz之间，现场试验中测试得到构架横向失稳频率主要集中10 Hz以下，因此仿真得到的结果与现场试验的结果相符。当动车组以300 km/h速度级运行时构架自身横向振动模态约为7 Hz。因此，构架横向加速度频率与构架自身横向模态相近时会造成构架振幅度增加[13−14]，从而降低构架横向稳定性。

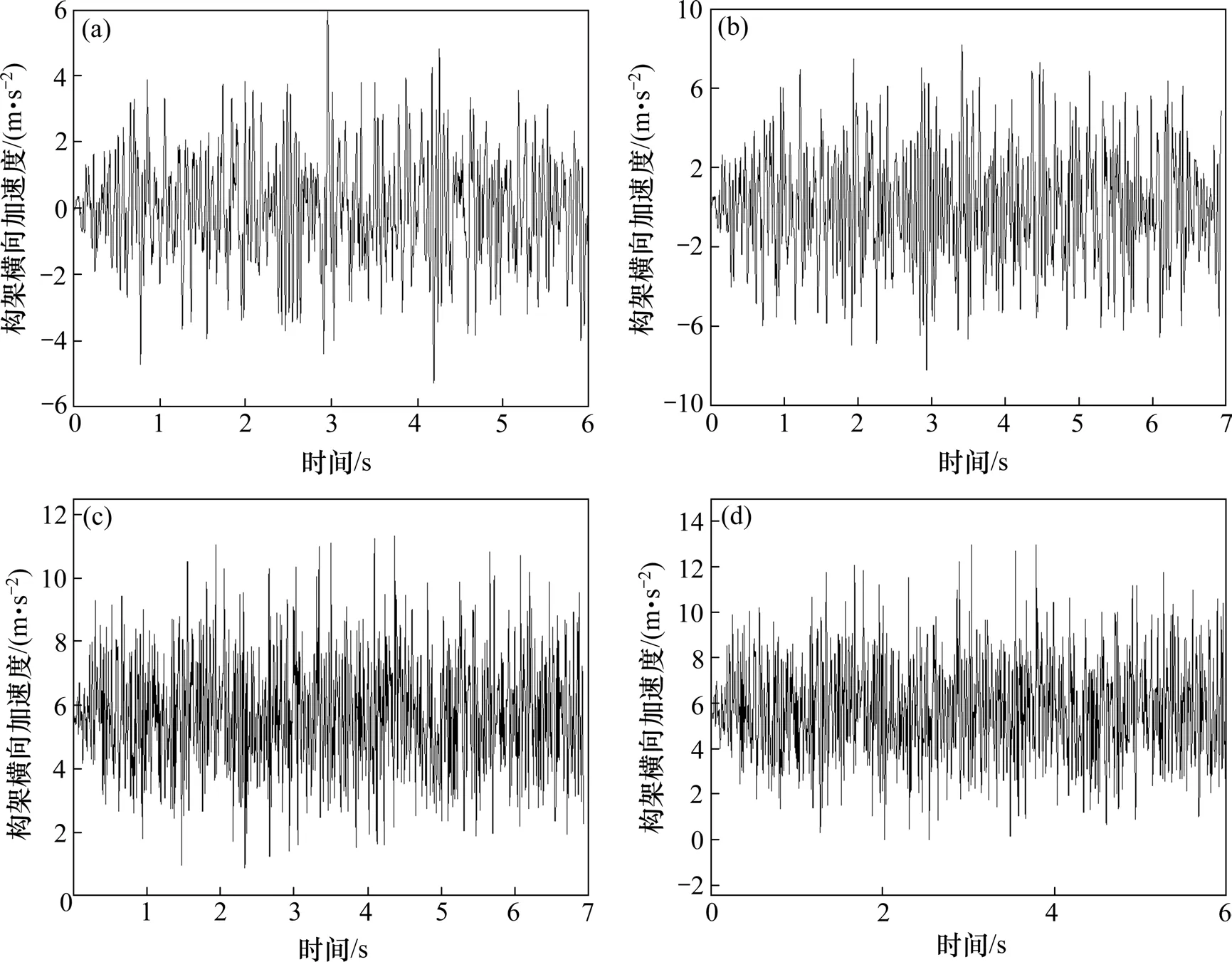
图5 构架横向加速度时域波形Fig.5 Time domain waveform of transverse acceleration of frame

图6 构架横向加速度功率谱密度图Fig.6 Power spectral density of transverse acceleration of the frame

2.2 波长对轮轨力的影响

动车组以100～350 km/h的速度级通过不同波长的波磨线路区段对轮轨垂向力的影响，如图7所示。

由图7可以看出，动车组以不同速度级通过波磨区段时，波长越小轮轨垂向力越大；一定波长时，动车组通过波磨区段时的运行速度越高轮轨垂向力越大。

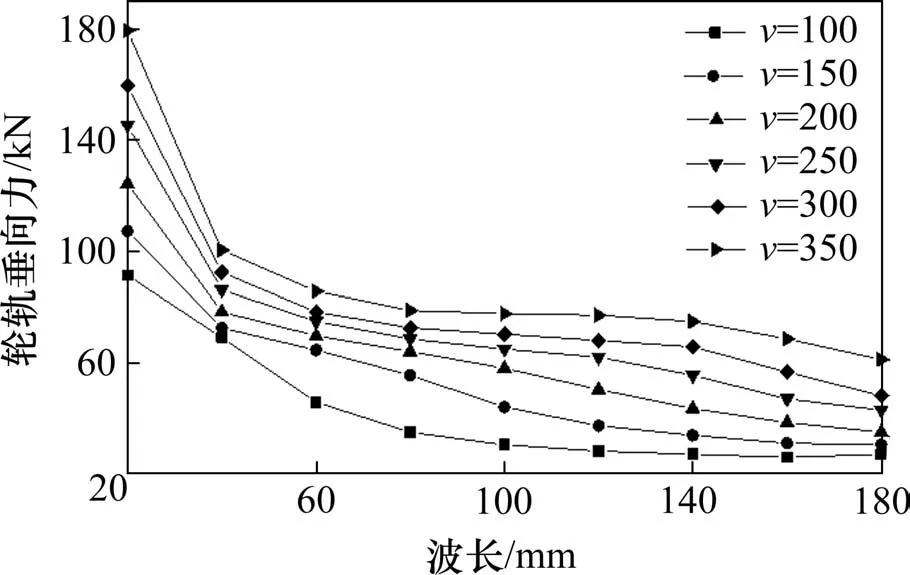
图7 不同波长对应的轮轨垂向力Fig.7 Vertical forces of wheels and rails corresponding to different wavelengths

2.3 波磨与轮轨力的关系分析

图8 和图9分别是动车组以300 km/h速度通过1阶和2阶波深区段车辆轮轨垂向力时域波形与波深对比图。

从图8和图9可以看出，高速动车组以300 km/h的速度通过不同波深区段时，轮轨垂向力最大值在15 kN至120 kN之间，轮轨垂向力均未达到轮重减载率的限值。1阶波深与2阶波深对应轮轨垂向力的波峰和波谷出现的位置与波深的波峰和波谷出现的位置不协同。即波磨波深的极值点出现位置与轮轨垂向力极值点出现位置没有明显对应关系。为了更加清晰地观察波深与轮轨力的关系，图10(a)和图11(a)分别给出1阶和2阶波深对应的波深时变率与轮轨垂向力的波形变化关系。

图8 1阶波深与轮轨垂向力的关系Fig.8 Relationship between first-order wave depth and vertical force of wheel-rail

图9 2阶波深与轮轨垂向力的关系Fig.9 Relationship between second order wave depth and vertical force of wheel-rail

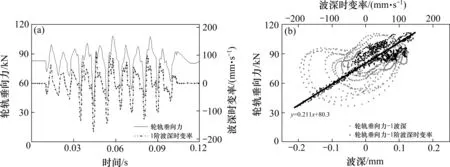
图10 轮轨垂向力与1阶波深时变率关系Fig.10 Relationship between vertical force and first-order wave depth-time variability

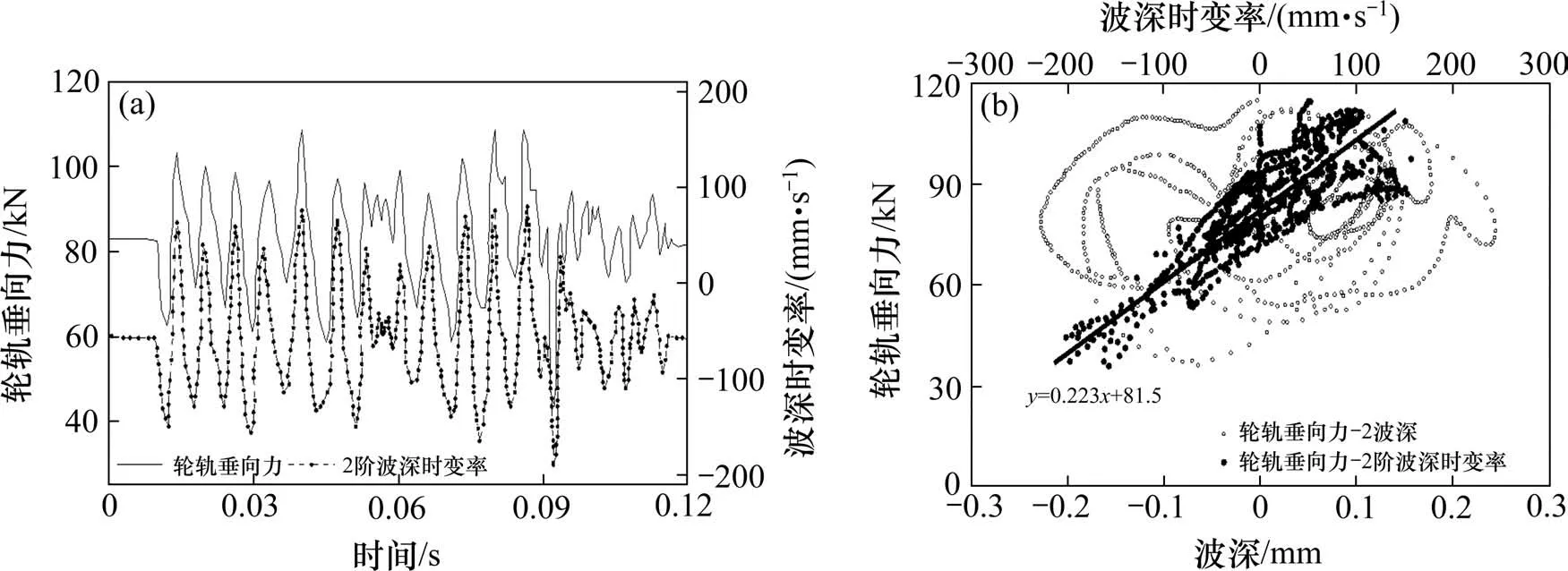
图11 轮轨垂向力与2阶波深时变率关系Fig.11 Relationship between the vertical force of the wheel-rail and the time-varying rate of the second order wave depth

由图10(a)和图11(a)中轮轨垂向力与相对应阶数的波深时变率波形关系可知，高速动车组通过1阶和2阶不同波深区段时轮轨垂向力波形与波深时变率波形变化具有较好的协同性，即波深时变率的波峰与波谷出现的位置与轮轨垂向力的波峰和波谷出现的位置具有一定的对应关系。因此，从波深时变率波形可以预测下一个轮轨垂向力幅值出现的位置。

由图10(b)和图11(b)中波深及不同阶数波深的波深时变率与轮轨垂向力关系散点图可以看出，不同波深时变率对应的轮轨垂向力的数据点较集中且存在一定的线性关系，该线性关系的斜率在0.211±0.02之间变化，拟合直线之间的斜率相差不大。因此，可以利用波深时变率波形来预测相同位置处轮轨垂向力的幅值。

2.4 波磨与钢轨加速度的关系分析

为了研究高速动车组通过波磨区段时波深对钢轨振动加速度的影响，图12(a)和图13(a)分别给出钢轨振动加速度与不同波磨波深及对应的波深时变率的关系。

图12 1阶波深及波深时变率与钢轨垂向加速度关系Fig.12 Relationship between first-order wave depth and time-varying rate of wave depth and vertical acceleration of rail

图13 2阶波深及波深时变率与钢轨垂向加速度关系Fig.13 Relationship between second order wave depth and time-varying rate of wave depth and vertical acceleration of rail

从图12(a)和图13(a)中的钢轨垂向加速度波形可以看出，钢轨垂向加速度波峰和波谷与1阶和2阶波深波形的波峰和波谷出现位置不存在对应关系。从图12(b)和图13(b)中钢轨加速度与波深及波深时变率关系散点图中可以看出，波深时变率与钢轨垂向加速度的数据点较集中，而波深与钢轨垂向加速度的数据点较离散。另一方面，波深时变率越大，钢轨垂向加速度数据点越离散，即钢轨加速度幅值越大[15]。因此，从数据点的分布来看波深及波深时变率对钢轨垂向加速度均不存在明显的对应关系。

3 线路试验结果分析

选取我国某条线路的波磨区段进行试验，如图14和 图15是 动车组 以300 km/h和350 km/h 2种不同速度级通过相同波磨区段的测试结果。

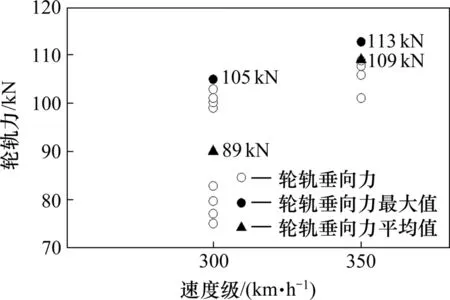
图14 波磨区段轮轨垂向力Fig.14 Vertical force of wheel-rail in rail corrugation section

图15 波磨区段钢轨垂向加速度Fig.15 Vertical acceleration of rail in rail corrugation section

由图14和图15可知，当动车组以300 km/h速度通过波磨测点时，轮轨力最大值105 kN，平均值89 kN；钢轨加速度最大值1 445 m/s2，平均值712 m/s2；当动车组以350 km/h速度通过波磨测点时，轮轨力最大值113 kN，平均值109 kN；钢轨加速度最大值1 852 m/s2，平均值1 511 m/s2；因此，由试验结果可以得出动车组通过波磨测点的速度越大轮轨垂向力越大，钢轨垂向加速度峰值也越大。

由图16和17可知，当动车组以300 km/h速度级通过1阶波磨测点时，轮轨力最大值105 kN，平均值89 kN；钢轨加速度最大值1 445 m/s2，平均值712 m/s2；当动车组以相同速度通过2阶波磨测点时，轮轨力最大值107 kN，平均值90 kN；钢轨加速度最大值1 503 m/s2，平均值750 m/s2；由此可得，动车组通过波磨区段的波深越大轮轨垂向力越大，钢轨加速度峰值也越大。

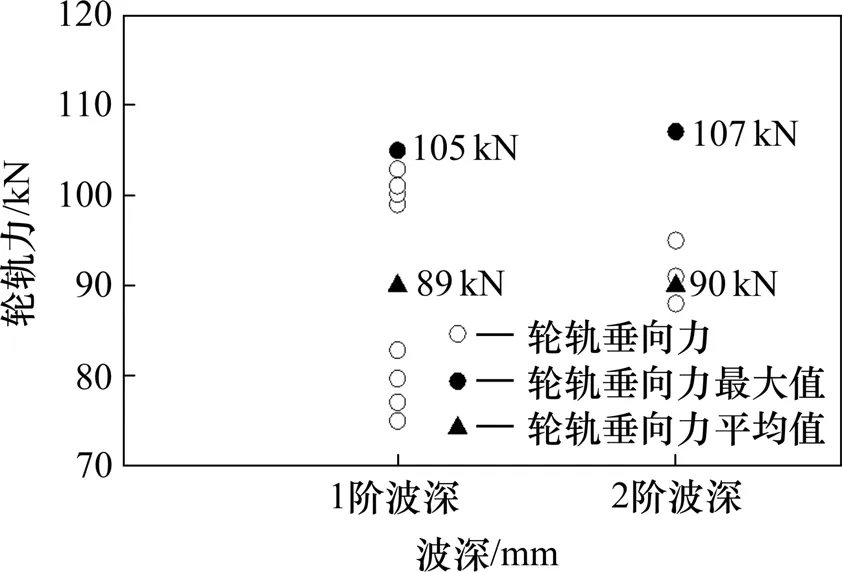
图16 不同波磨区段轮轨垂向力Fig.16 Vertical force of wheel-rail in different rail corrugation sections

图17 不同波磨区段钢轨垂向加速度Fig.17 Vertical acceleration of rail in different rail corrugation sections

4 结论

1)动车组以一定速度通过波磨区段时车辆系统的构架横向加速度和轮轴横向力随钢轨波磨波深的增大而增大。当波深一定时，车辆通过波磨区段速度越高，构架横向加速度及轮轴横向力越大。

2)波深时变率是影响车体构架稳定性的主要因素，不同波深的波深变率对应的构架横向加速度功率谱密度主要集中在5～6.5 Hz之间。试验结果表明当动车组以300 km/h运行时车辆构架自身横向模态约为7 Hz。构架横向加速度频率与构架自身横向模态接近时会造成构架振动幅度增加，从而降低构架横向稳定性。

3)钢轨波磨的波长越大对应的轮轨垂向力越小；当波长一定时，动车组运行速度越高轮轨垂向力幅值越大。

4)波深与轮轨垂向力以及钢轨垂向加速度波形没有对应关系，波磨时变率与轮轨垂向力以及钢轨垂向加速度存在比较明显的对应关系。因此，可以通过波深时变率波形预测轮轨垂向力幅值，以及轮轨力幅值出现的位置，为钢轨打磨标准提供帮助。