起伏输油管道临界完全携积水油速数值模拟
李岩松, 丁鼎倩, 韩 东, 刘 静, 梁永图
(1. 中国石油大学(北京) 城市油气输配北京市重点实验室,北京 102249; 2. 美国加州大学圣地亚哥分校 机械与航空工程系,美国 圣地亚哥 92093-0411;3. 中国石化销售有限公司华南分公司,广州 510000;4. 清华大学 工程力学系,北京 100084)
目前,石油产品的运输方式主要有空运、水运、公路运输、铁路运输及管道运输.其中,管道运输具有费用低、可靠性高、自动化程度高、输送能力大以及油品损耗率低等优点,已成为石油产品的最主要运输方式[1-2].在成品油管道运行过程中,管内油品所携带的游离水在一定温压和流速条件下会从油流中分离出来,聚集在管道沿线低洼位置,形成积液和固体颗粒杂质[3].当油品流经积水位置时,管内积水会严重影响油品的质量指标,如油品洁净度、电导率、水分离指数等[4-7].因此,研究成品油管道内积水的高效清除方法具有十分重要的工程意义.
国内外部分学者借鉴气藏连续携液[8]、浆液管道输送[9]以及钻井液携带岩屑[10]的相关理论,提出了一种利用油流的剪切作用,将管道低洼处的积水携带出管道的“清管”方法.该方法只需通过调节管道入口压力和流量,而不需要依靠清管器就可实现清除管内积水和固体杂质的目的,因此这种清管方式又被称为水力清管[11-13].
临界携水油速是指管内积水开始进入上倾管段时的最小油速[14-16],为了便于数值计算,Magnini等[14]将油流携水量为积水总量5%时的管内最小油速定义为临界携水油速,其是制定管道水力清管方案的必需参数.国内外学者对临界携水油速进行了大量研究.Xu等[15-16]和Song等[17]建立了油携水的二维仿真模型,利用ANSYS Fluent中的Volume of Fluid(VOF)模型分别研究了管道倾角、管道直径、积水体积、油相密度对临界携水油速和携水体积的影响.Magnini等[14]指出水相与管壁的润湿性能对初始状态下管道底部积水的存在形态影响很大,进而影响了初始状态下管内积水的厚度.为此,Magnini等[14]基于OpenFOAM建立了三维油携水仿真模型,通过VOF模型研究了不同润湿性条件、油速、积水体积对积水移动特性及油水两相流型的影响.
虽然,临界携水油速对研究油携水过程具有重要的借鉴作用,但从工程应用的角度出发,若管内积水无法被完全携带出管道,残留在管内的积水依然会加速管道的内腐蚀,因此工程应用中更加关注如何获得实现管内积水全携带时所需的最小油速.由此可知,研究临界完全携积水油速的计算方法更具有工程价值.鉴于此,本文在当前油携水相关研究成果的基础上,深入分析了水团在上倾管道中的运动特性,建立了上倾管道临界完全携积水的数值模型,提出了模型的求解算法,并通过文献数据验证了模型及求解算法的可靠性.最后,详细研究了上倾管道中油携水波状分层流动过程,给出了上倾管道临界完全携积水油速的数值判据.
1 完全携水流动型态
管内临界完全携积水油速是水力清除管内全部积水所需的最小携水油速,故分析完全携水条件下油水两相流动型态可在一定程度上反映临界完全携积水条件下管内的流动特性.Magnini等[14]通过数值模拟方法研究了管内不同体积积水(15、25、40 mL)在不同润湿角(30°、90°、120°)条件下的水力携带过程,获得了清除全部积水时,管内不同油相折算速度(0.18、0.20、0.25 m/s)下,水团在上倾管道中的平均速度以及平均水相高度,详细数据可参考文献[14].
上倾管道中油携水流动如图1所示.其中:D为管道直径;vw为水团在上倾管道中的平均移动速度;lint为油水界面在管道截面上的半长度;hw为水相平均高度.根据图1管道截面中的几何关系可知,水相流通面积Aw与hw之间的关系为
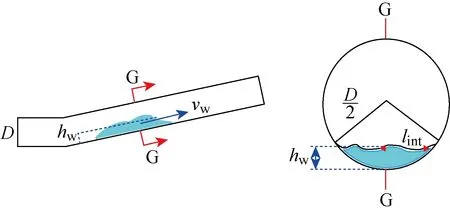
图1 上倾管道中油携水流动示意图
(1)
油水两相的流型一般取决于油相折算速度vso和水相折算速度vsw的相对大小,水相折算速度可表示为
(2)
式中:Ap为管道的横截面积.由式(2)即可将文献[14]油携水流动过程中的水相平均速度转换为水相折算速度.
Hanafizadeh等[18]在管径为20 mm,管长为6 m,倾角为12° 的实验环道上进行了油水两相流流型的观测,并绘制了流型图.需要说明的是,油水两相流流型除了与油水两相的折算速度有关外,还受到管道倾角、流体物性、管道直径的影响,但Hanafizadeh等[18]和Magnini等[14]的研究中油水物性、管道参数基本相同,故可近似利用Hanafizadeh等[18]的流型图来确定上倾管道内油携水的流动型态.文献[14]中的油携水流动工况在油水两相流型图中所处的位置如图2所示.
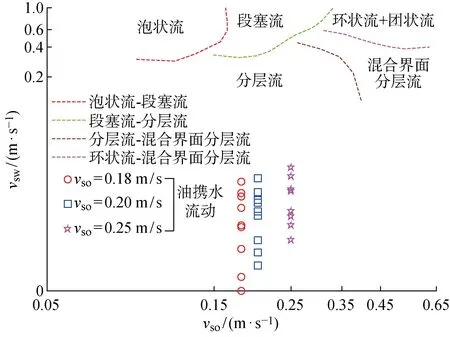
图2 完全携水油速下,上倾管道中的油携水流动型态[14,18]
由图2可知,在Magnini等[14]的研究中,完全携水条件下上倾管道内油携水属于分层流.这主要是由于管道内积水较少,水相近似以水膜的形式吸附在管壁上.在靠近管壁附近的区域,由于流动边界层的影响,油水界面处油相的速度较小,相界面处油水之间的剪切力较小,水相在较小的剪切作用下不足以被破碎为小水滴,所以在上倾管道油携水过程中,油水两相呈现分层流的流型.
此外,根据Kelvin-Helmholtz油水界面稳定性理论可知,当油相速度低于使界面失稳的临界油速时,水相可稳定沉积在管道底部,而不随油流前行[19];而在完全携水条件下,油相速度大于油水界面稳定状态下的临界油速,故此时油水相界面必然失稳,相界面呈现波动形态.综上所述,在完全携水油速下,上倾管内油携水流动属于局部油水两相波状分层流.
2 数值模型及求解算法
2.1 油携水波状分层流的数理模型
成品油管道洁净程度较高,管内一般仅存在少量的积水[20],积水高度较小,在管壁边界层的作用下,靠近管壁附近处的油流速度较小,不足以使将附着在管道底部的积水完全破碎成分散相进入油相随之流动,而是以偏心大水滴[16]的形式在上倾管道中随油流向管道出口缓慢迁移,如图3所示.其中:θ为管道倾角;Lw为水膜在上倾管道中的长度.
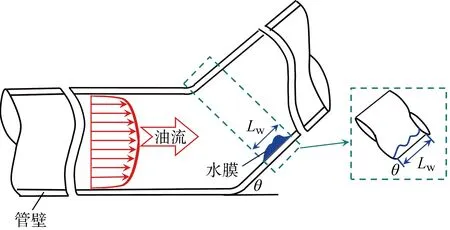
图3 上倾管道中油携水波状分层流的物理模型
油携水分层波状流动的控制方程包括质量守恒方程、动量方程、波状相界面模型和积水平均高度模型.
2.1.1质量守恒方程 由于成品油管道中积水含量较少,不考虑油水间的乳化作用,即不考虑水相对油相质量流量的影响,所以在管道轴向的每个截面上,油相总质量流量保持不变.油相质量守恒方程可以表示为
(3)
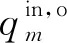
2.1.2动量方程 由于管道径向速度远小于管道轴向速度,可忽略径向速度的影响.此外,管内积水一般聚集在距离管道入口较远的低洼位置,管内油流流动已处于稳定的充分发展状态.成品油管道中流量较大,管内油相处于高雷诺数的湍流状态,而靠近管壁的水膜由于移动速度较小,一般处于低雷诺数流动状态.大涡模拟(LES)方法适用于研究不同雷诺数下的流动模拟[21-23].鉴于此,本文采用LES方法模拟成品油管道油携水流动过程中油相的湍流流动.处于充分发展状态的油、水两相轴向滤波动量方程为
(4)
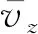
LES方法中的亚格子湍流黏度为
(5)
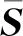
在近管壁和相界面附近需要考虑流动边界层对湍流的影响,亚格子湍流黏度中可用衰减函数DS来反映壁面附近湍流的衰弱.衰减函数DS为
DS=1-e-(y+/C+)
(6)
式中:y+为离开壁面或相界面的无量纲距离;C+为经验常数,一般取C+=25.在y+较小时,DS的计算式为
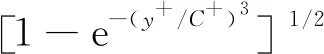
(7)
离开壁面或相界面的无量纲距离y+的计算公式为
(8)
(9)
dint=|y|
(10)
式中:n为油水界面的法向量.
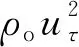
综上,无量纲质量守恒方程和动量方程为
(12)
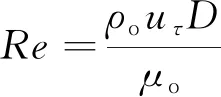
2.1.3波状相界面模型 上倾管道油携水流动属于波状分层流.在油携水波状分层流动过程中,界面波动会导致油水相界面处流动阻力增加,湍流强度在相界面处无法完全衰减,这意味着需要对LES方法亚格子湍流黏度模型中油水界面附近的有效距离进行修正.
Rotta[24]提出可通过在流场计算节点到油水相界面的有效距离(见式(8))中增加一个偏移距离Δy来增加波状相界面处的湍流强度,即
dint=|y+Δy|
(13)
将波状相界上的界面波动等效为砂粒粗糙度可有效描述界面波动对湍流流场的影响.无量纲等效Nikuradse砂粒粗糙度Ra+和无量纲偏移距离Δy+的计算公式分别如下式所示:
(14)
(15)
油水界面的等效Nikuradse砂粒粗糙度Ra的计算方法为[25]
(16)
(17)
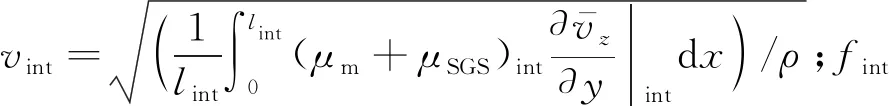
2.1.4管内积水平均高度模型 成品油管道在临界完全携积水油速下,进入上倾管道中的积水以大水滴的形式存在,此时若要求解水相流通面积上的速度分布,则首先需要计算水团的平均高度.上倾管道中水团的高度取决于油水相界面的表面张力、重力、界面剪切力以及水滴与管壁间的润湿性能等因素的复杂综合作用.De Gennes等[26]提出当油相对水相的携带作用较弱时,可利用静态条件下水团在水平管道中的铺展高度来近似其在油流弱剪切扰动下的平均高度,计算公式为
hw=
(18)
式中:Vw为管道内积水体积;β为水团与管壁的润湿角;Bo为邦德数,无量纲,反映了界面张力和重力的相对大小;σ为油水界面张力;Rw为假设水团为球形时对应的曲率半径;Δρ为油水两相的密度差.
在Bo≫1时,当水膜进入上倾管道后,由于倾角的影响,与油水界面正交方向上的重力分量减小,所以会导致水相高度相比于水平管道有所增厚.考虑倾角影响的上倾管道中水膜高度计算模型[26]如下所示:
(19)
式中:Ch为模型系数.当管径较大时,管壁曲率半径较大,与平板接近,此时取Ch=2.0.
管径对水膜高度存在影响,但对于输油管道而言,由于管道内介质较为清洁,管内的积水体积一般较小,所形成的水膜厚度也较小,且成品油管道的管径一般较大(可达几百毫米),所以水膜在管道底部铺展开时,水膜与管壁的接触面积相比于管道内壁面积较小,可近似忽略管径曲率对水膜铺展高度的影响.因此,管径越大,水膜在管道内的铺展状态越接近于平面,所提出的水膜高度模型在计算大管径内水膜高度时计算误差越小.
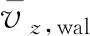

表1 边界条件
2.2 数值求解算法
2.2.1坐标变换 Charles等[27]直接在笛卡尔坐标系下利用结构化网格对管道截面进行离散,但由于管壁的非规则特性,导致需要人为重构管壁节点,为数值计算结果引入误差.为解决多相管流存在相界面的特点,部分学者将双极坐标引入气液两相流的数值计算[28-30].在双极坐标系中,管壁以及相界面可通过直线表示以便于计算.鉴于此,本文亦采用双极坐标系下的结构化网格离散计算区域,将非规则的管道区域(见图4(a))转变为规则的有限矩形区域(见图4(b)),并基于坐标转换规则,离散控制方程.其中:η和ξ分别为直角坐标系x和y轴在双极坐标系中对应的坐标轴;P1~P4分别为两种坐标系互为对应的特征节点.
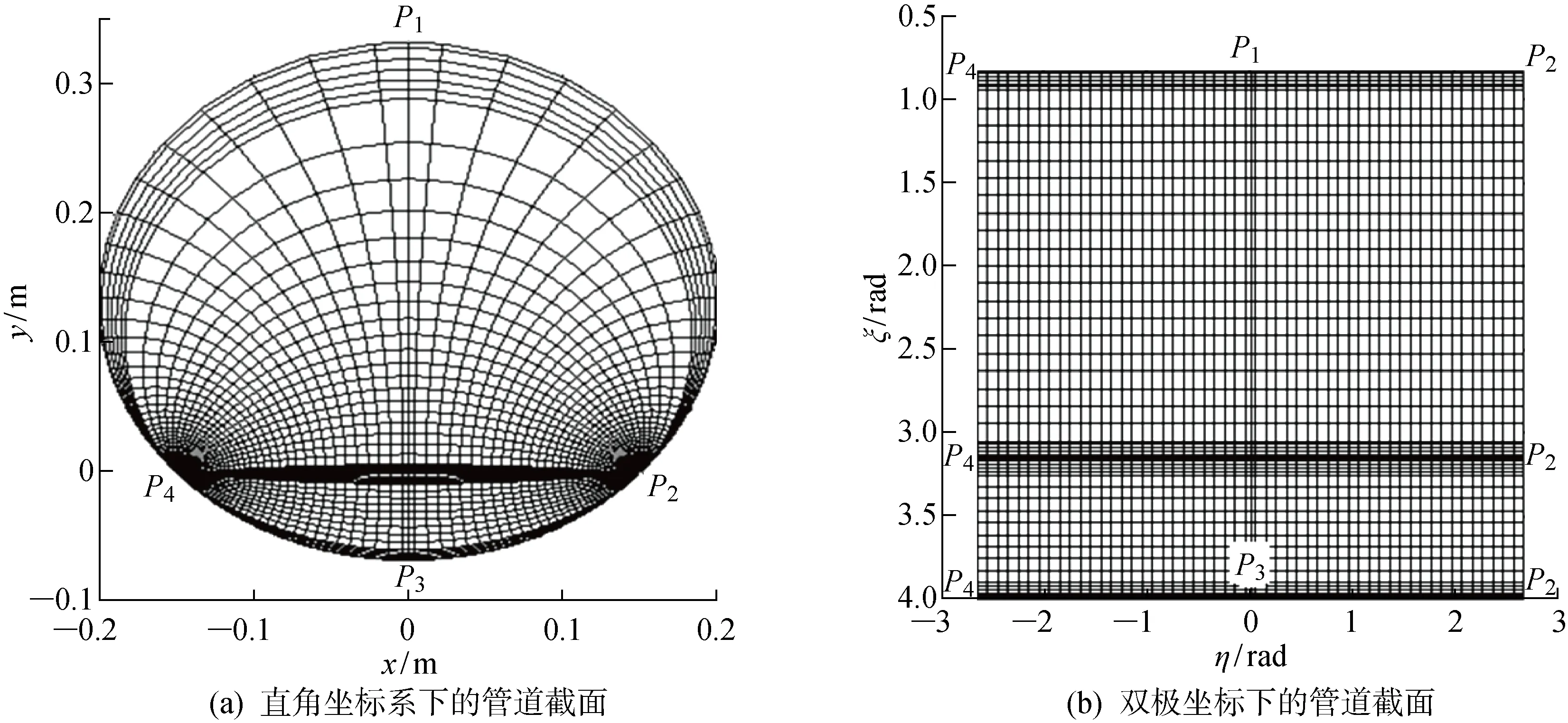
图4 坐标变换
控制方程采用有限容积法(FVM)进行离散,其中对流项采用二阶迎风格式离散,扩散项采用二阶中心差分格式离散.
2.2.2动量方程压力梯度求解方法 管道截面流场的求解属于压力和速度耦合问题.压力和速度耦合问题的求解算法主要有SIMPLE系列算法、IDEAL[31]算法以及MAC[32]算法等,上述算法主要用于求解压力场和速度场的细节信息,而本文的主要目的是计算积水进入上倾管道后,水团在油相携带下迁移的轴向速度.相比于轴向速度,管道中流体径向速度很小,故为提高计算效率,假设管道同一截面上压力相等,不考虑管道截面二次流引起的压力变化,即不对管道截面上的压力场进行全分辨求解.
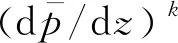
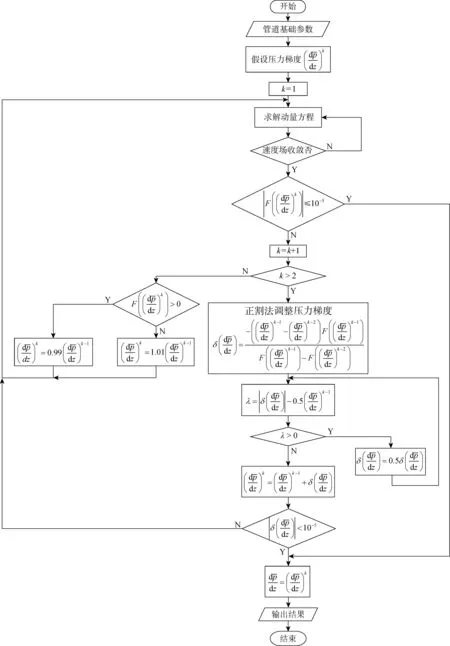
图5 基于正割法的压力梯度求解算法程序框图
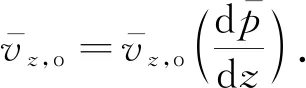
(20)
式(20)为高度非线性方程,其导数计算较为复杂,该类方程可采用正割法求解.正割法迭代公式如下:
2.2.3油携水模型的整体数值求解算法 成品油管道油携水两相管流是复杂的油水两相波状分层流过程,需要耦合求解质量守恒方程、动量方程、波状界面模型以及水相高度模型.管道截面的速度场、压力梯度、剪切速率等参数需要迭代求解直至全部收敛.控制方程组的求解算法如图6所示.
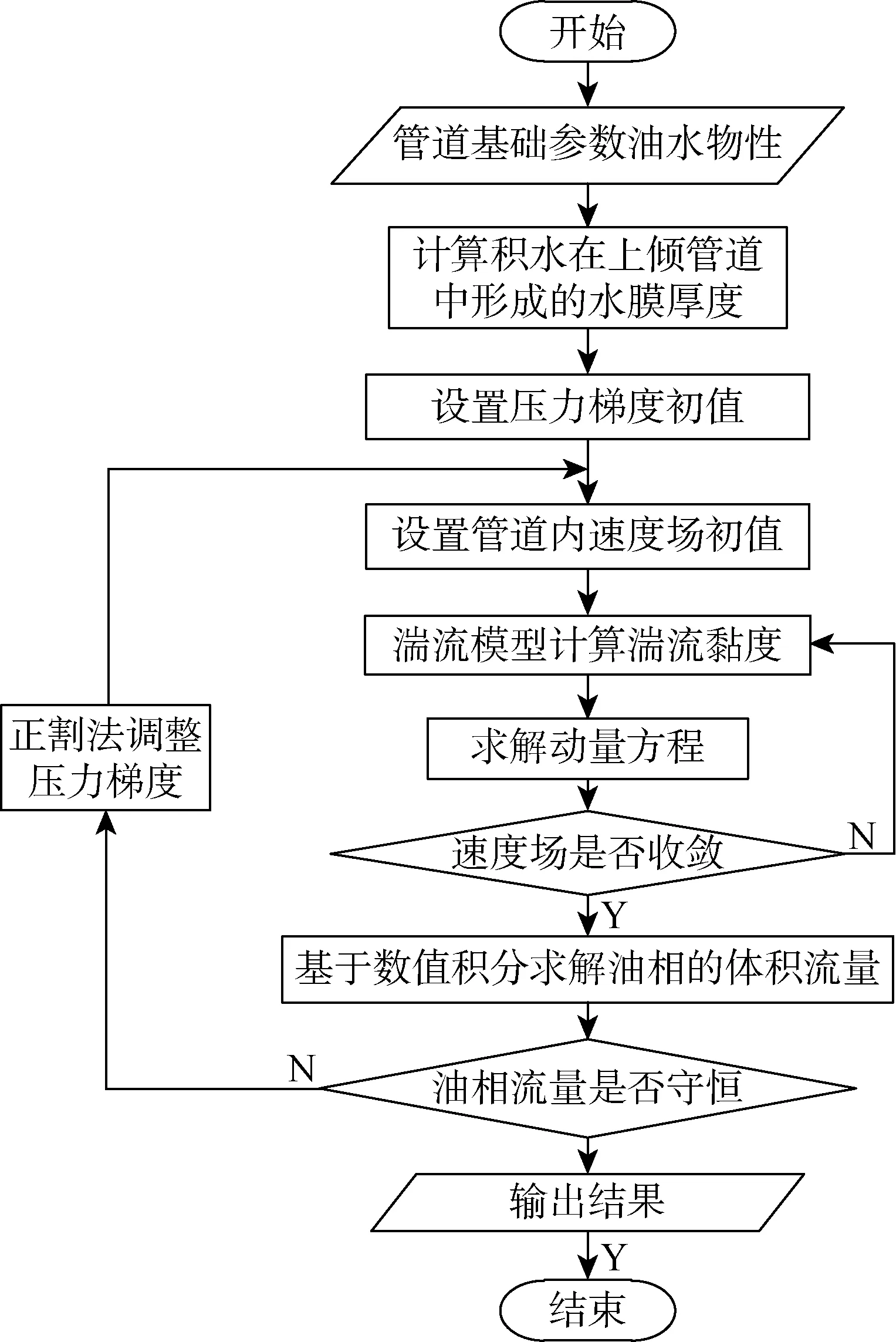
图6 油携水模型的整体数值求解算法程序框图
求解步骤如下:
(1) 设定管道基础参数,如管径、管长、管道倾角、积水和管壁的接触角以及管道入口油相的折算速度等;
(2) 设定当前管道截面速度场和压力梯度的初值,并基于湍流模型计算相应的流体物性以及湍流黏度;
(3) 依次耦合迭代求解速度场和湍流黏度,直至全部收敛后,执行步骤(4);
(4) 基于双极坐标下的积分公式,求解当前截面的油相体积流量.若油相体积流量守恒,即油相连续性方程收敛,则计算结束;反之,调用基于正割法的压力梯度求解算法调整压力梯度,并返回步骤(2),直至油相连续性方程收敛.
3 模型验证
3.1 管内积水水膜平均高度模型验证
本文通过与Magnini等[14]的数值计算结果进行对比,验证管内积水水膜平均高度模型的适用性,不同积水体积以及不同油相速度下,上倾管道中的水膜平均高度模型计算值(E1)与相同条件下Magnini等[14]的模拟结果(E2)的对比分析如图7所示.
由图7可知,该模型的计算结果与Magnini等[14]的模拟结果基本吻合,验证了水膜高度模型的可靠性.从图7中还可以看出,当积水体积和油相速度一定时,水膜与管壁的接触角越大,模型计算误差越小.这是由于水膜与管壁的润湿角越大,水膜与壁面的接触面积越小,水膜高度受管道内壁曲率的影响也越小,所以模型的计算误差也越小.上述现象说明水膜高度模型更适用于计算管内壁为疏水特性的管道内积水平均高度.
通过对比相同油速下水膜高度的计算结果(见图7(a)~7(c))可以看出,当积水体积越大时,模型的计算结果误差也越大.这是因为图7中所采用的管道直径较小(27 mm),积水体积越大,水膜在管道底部铺展的高度受管壁曲率影响也越大;而式(19)中假设管道壁面为平板,因此积水体积越大,管内水膜高度的计算误差也越大.需要说明的是,工业成品油管道中沉积在管道底部的积水体积较小,且管径较大,这为利用式(19)计算水力清管过程中水膜平均高度提供了有利因素.
对比图7中不同油速下的模型计算误差还可发现,在模型计算误差相近的条件下,随着油速的增大,水膜高度模型系数Ch越小,即在油速较高的情况下,无需调整模型系数Ch,将其取为原始公式中Ch=2.0也可获得较好的计算结果.这是因为管内油速越大,油相对积水的剪切作用越强,水膜在油相剪切作用下被拉长,导致水膜高度越低,油水相界面越靠近管壁区域,而管壁附近的油相剪切作用反而越小,此时水膜的形成过程越接近静态条件下水膜自由铺展的情形,所以模型系数Ch也越接近原始值.对于成品油管道而言,管内油速一般较大(1~2 m/s),因此,在进行成品油管道水力清管计算时可近似取Ch=2.0.
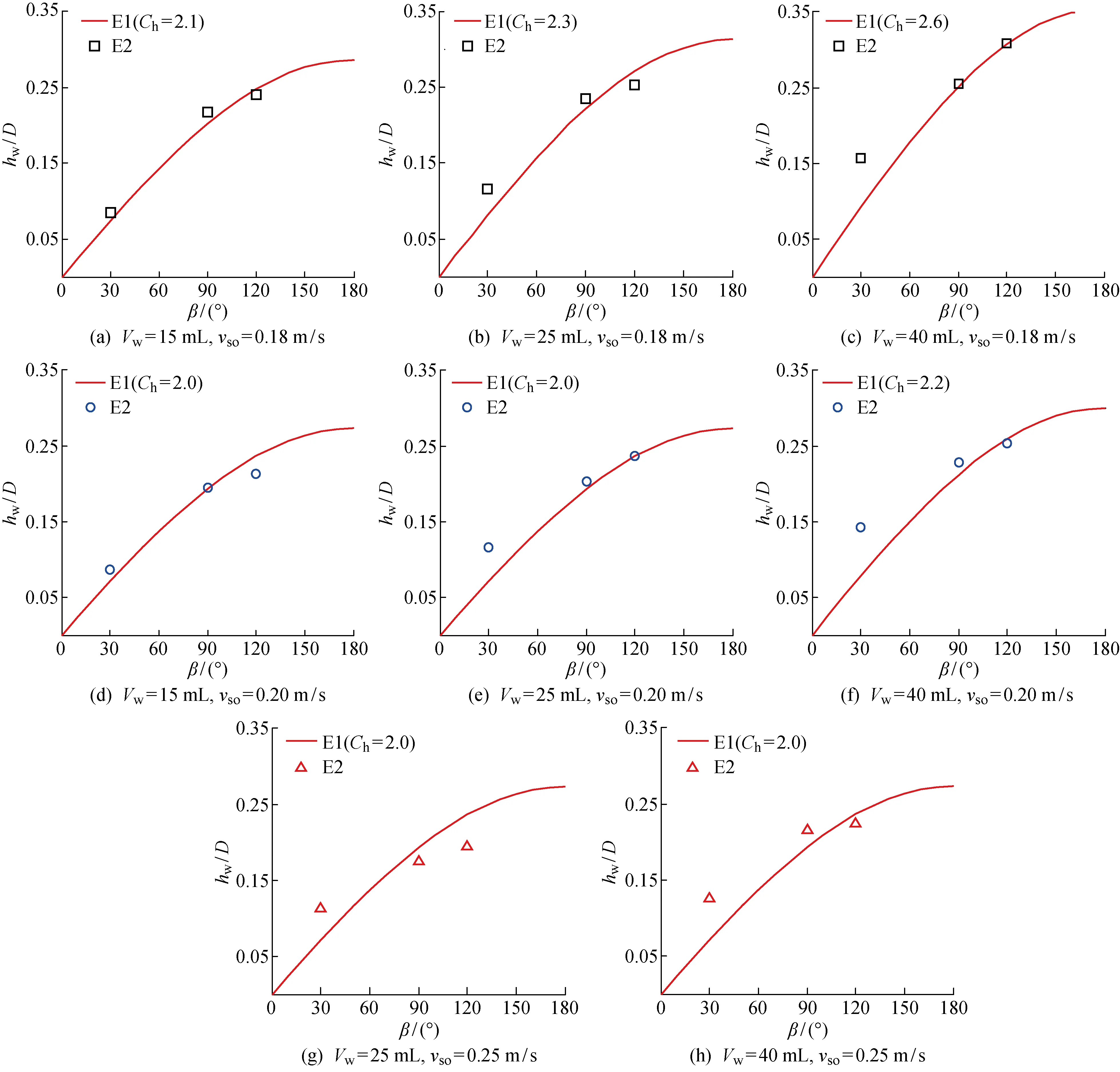
图7 E1与E2的对比
综上所述,利用式(19)估算成品油管道水力清管过程中水膜的平均高度是可行的.
3.2 上倾管道内油携水波状分层流验证
通过对比相同参数条件下,上倾管道内油携水流动过程中管道截面中垂线速度分布文献[15]计算值与本文提出的油携水波状分层流模型(WSFM-TWLEOS)计算值,以验证WSFM-TWLEOS的有效性.文献[15]中所计算的管道直径为27 mm,管道倾角为12°,管道入口油相折算速度vso=0.03 m/s,其他参数可参考文献[15].文献计算结果(E3)与WSFM-TWLEOS计算结果(E4)对比如图8所示.
由图8可以看出,所提WSFM-TWLEOS计算值与文献计算值基本吻合,特别是管内逆流水团的移动速度与文献计算值近似完全一致.但油相速度的计算值与文献值存在一定误差,这主要是因为文献[15]采用三维非稳态模型进行全流场模拟,而本文在求解油携水流动过程中忽略了管道径向的油相速度,且未考虑水团对油相流动影响,所以WSFM-TWLEOS存在一定的计算误差.但总体而言,WSFM-TWLEOS的计算精度基本满足工程需求.需要特别指出,所建立的模型针对水团运动速度的计算精度较高.上倾管道中临界完全携积水油速的确定主要是通过水相的速度分布特征来判断的,由此可知,基于WSFM-TWLEOS来计算上倾管道内临界完全携积水油速是可靠的.
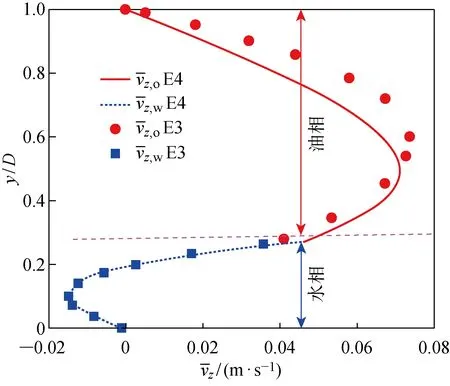
图8 上倾管道内油携水流动过程验证
4 临界完全携积水油速
4.1 基础参数
分别计算了管道入口处油相的折算速度为vso=0.1、0.5、1.0、1.5、2.0 m/s时管道横截面上的油水两相的速度分布.在本节的数值研究中,管径为100 mm,管道倾角为12°,油水界面张力为18.33 N/m.如前所述,成品管道水力清管中一般利用柴油批次携带管内积水,故将研究柴油携带水团的流动过程.柴油的密度为856 kg/m3,黏度为3.43 mPa·s,水相的密度为988.88 kg/m3,水相黏度为0.597 mPa·s.假设管壁为疏水性壁面,水团与管壁间的接触角为120°.
4.2 低油速下上倾管中水团流动特性
低油相折算速度(vso=0.1 m/s)时,上倾管道截面上的速度场分布如图9所示.由图9可以看出,相比于水平管道内油水两相流动的油相速度分布,上倾管道截面上油相速度最大值位置向相界面方向偏移(见图9(b)),这是由于油相在经过弯管进入上倾管道后,油流受到的重力影响增大,油相速度最大值在重力的作用下向管道底部方向偏移.上述油相在上倾管道中的速度分布特性有利于管道底部积水的携带,上倾管道中油相速度最大值向油水界面位置偏移后,油水界面上的剪切力增大,油相对水相的剪切携带作用增强.
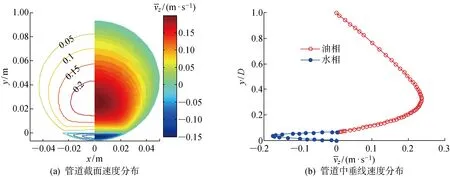
图9 vso=0.1 m/s时管道截面速度分布
从图9(b)中还可以看出,当油相速度较小时(vso=0.1 m/s),水相的速度与上游来油的流动方向相反,水相区域内各点的速度均为负值,这意味着水团重新流向管道低洼处,此时无法实现管道内积水的水力驱除.这是由于油相速度较小,油相在相界面上对水相的剪切力较小,不足以克服上倾管道中水团的重力.水相速度的最大绝对值出现在油水相界面与管道底部的中间位置,即水相流动区域的中心位置,管道中垂线水相速度呈现抛物线分布,这与Song等[5]的研究结果一致,进一步验证了所提WSFM-TWLEOS的正确性.
根据上倾管道内水相的速度场可知,水膜的平均速度为
(21)
水相的雷诺数为
(22)
式中:ρw为水相密度;Dw为水相的水力直径;νw为水相的运动黏性系数.以水力光滑区计算可知,在数值算例参数条件下,水团流动过程中由流动引起的摩阻压降和重力引起的压降分别为
(23)
(24)
由式(26)和(27)可知,水相的流动过程主要受重力压降的影响,摩阻压降相比于重力压降可忽略,这表明水力清除积水过程中油流的剪切作用主要用于克服重力压降.
综上所述,较小油速下,上倾管道中的水膜在重力作用下会重新回流至管道低洼处,故要实现积水的完全水力驱除,需要不断调整油速,直至水膜流动区域内水相速度均大于0.
4.3 上倾管内临界完全携积水油速数值判据
上倾管道临界完全携积水流速的物理意义是指积水全部进入上倾管道,并被油流全部携带出管道时所需的最小油速.上述水相速度分布特征即为临界完全携积水油速的数值确定方法.
不同油相折算速度(vso=0.25~2.0 m/s)下,上倾管道截面的速度分布如图10和11所示.由图10可知,不同油相折算速度下管道截面上油相速度分布特性相似,而水相速度差异较大.从图11(a)~11(c)可知,靠近相界面处的水相部分在油相的携带作用下向下游流动,而靠近管壁底部的水相部分由于油相剪切不足以克服重力作用,致使部分水相回流至管道底部.随着油相速度的增大,油相在油水相界面上的剪切力增大,油相对水相的携带作用增强,随油流向下游流动的积水体积逐渐增多.
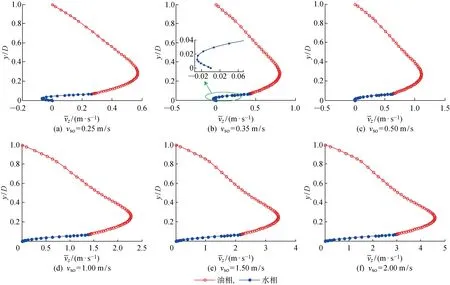
图11 不同油速下,上倾管道截面中垂线速度分布
对比图11(b)和11(d)还可以发现,油相速度越大,水相速度最小值(负值)位置逐渐向管壁偏移,当水相速度的最小值出现在管壁位置时,此时管内油相速度即为临界完全携积水油速,上述研究结果即上倾管道中油流取得临界完全携积水油速的数值判据.在本文的数值算例中,临界完全携积水油速为0.5 m/s.从图11(e)和11(f)中还可以看出,在临界完全携积水流动状态下,水相在管道中垂线上的速度从管壁到相界面近似呈线性增大,并在相界面处达到最大.
5 结论
本文首先分析了完全携水油速下管内油携水的流动型态,建立了一种高效的油携水分层波状流动的拟三维准稳态数值模型,首次给出了临界完全携积水油速的数值判据.对上倾管道内油携水流动过程进行了数值研究,得出如下主要结论.
(1) 在临界完全携积水油速下,上倾管内油携水流动属于油水两相波状分层流.
(2) 相比于水平管道内油水两相流动的油相速度分布,在重力作用下,上倾管道截面上油相速度最大值位置向相界面方向偏移,水团在流动过程中主要受到重力压降的影响,摩阻压降相比于重力压降可忽略.
(3) 管内油速较低时,靠近相界面处的水相部分在油相的携带作用下向下游流动,而靠近管壁底部的水相部分由于剪切作用不足以克服重力影响,水相在重力作用下回流至管道底部,随着油相速度的增大,油相在油水相界面上的剪切力增大,对水相的携带作用增强,积水被携带出管道的体积增大.
(4) 油相速度越大,水相速度最小值(负值)位置逐渐向管壁偏移,当水相速度的最小值首次出现在管壁位置时,对应的管内油相速度为临界完全携积水油速.

