考虑蒙皮透射率的飞艇热力学模型及其热特性

程 晨， 王晓亮

(上海交通大学 航空航天学院， 上海 200240)

平流层飞艇在工作过程中，外界热环境复杂且具有时变性.平流层空气稀薄，因此飞艇一般体积都很庞大，在驻空飞行过程中，其热特性受自身材料热特性、外部环境热源及囊体内外换热方式的影响极大.强烈的太阳辐射和微弱的对流换热导致飞艇蒙皮及内部气囊内温度场昼夜温差很大，从而影响飞艇的浮力和蒙皮的应力水平，改变其驻空高度、飞行姿态及轨迹，局部过热和应力增大也可能会导致蒙皮的膨胀变形乃至破坏.因此建立准确的飞艇热特性模型，掌握及预测飞艇蒙皮及内部填充气体的温度，对于飞艇设计及控制有着重要的意义.

20世纪80年代，国外许多学者就开始研究飞艇热特性.近年来，国内学者对平流层飞艇热特性模型的研究也在持续发展，取得了一定的成果[1].文献[2]建立了瞬态运动方程和传热模型.文献[3]用Fluent软件对飞艇进行了仿真分析.文献[4]研究发现相同条件下南瓜形气球的氦气温度及蒙皮平均温度均高于球形气球.文献[5]详细研究了飞艇晴空时的太阳辐射、长波辐射以及强迫换热模型.文献[6]分析了驻空期间太阳电池等效面积热阻、转换效率及铺装面积对飞艇热温度昼夜变化规律的影响.

目前飞艇热特性的主要研究方法可以分成两大类：集总参数法和分布参数法.集总参数法是将飞艇看成一个或几个温度均匀分布的部分进行研究，飞艇蒙皮及内部填充气体的热特性仅仅随着时刻的变化而变化，与具体的坐标位置无关.分布参数法则首先需要将蒙皮表面网格化，考虑热源强度与蒙皮空间位置的相关性，再分别计算每一个蒙皮单元的热特性.集总参数法的计算结果较为粗略，但是计算速度较快，适用于计算上升、下降时的飞艇状态[7-9]，分布参数法相较于集总参数法计算量更大，但是计算结果更为准确，更适用于计算飞艇驻空状态时的热特性[10-12].

在现有的研究中，绝大多数学者在分析内部填充气体的热特性时，只计算了气体与蒙皮内表面之间的自然对流换热，未考虑实际情况下飞艇蒙皮材料的透射特性以及内部填充气体对于辐射的吸收率与发射率，忽略了各类辐射对内部填充气体热特性的直接影响，因此传统模型只适用于计算蒙皮为完全不透明材料的飞艇热力学特性.本文在建立飞艇热力学特性模型时，考虑了蒙皮的透射特性，给出了新的蒙皮单元遮挡系数的计算方法，同时也研究了外部辐射热源对于飞艇内部填充气体热特性的影响，并补充计算了蒙皮与内部填充气体之间的辐射换热.本文采用有限拆分法来实现对模型的数值计算，即在分析内部填充气体热特性时采用集总参数法，在分析表面热特性时采用分布参数法，在保证计算精度的前提下，提高了计算效率.

1 考虑蒙皮透射率的飞艇热力学模型

影响平流层飞艇热力学特性的热源及换热方式可分为太阳短波辐射、太阳长波辐射以及对流换热.

1.1 飞艇热特性模型耦合机制

目前，大部分学者在研究平流层飞艇热特性模型时，对飞艇蒙皮材料以及内部填充气体的特性做了以下简化处理：

(1) 忽略了蒙皮对辐射的透射特性，外部辐射无法透射穿过蒙皮表面，只会作用在不被遮挡的蒙皮单元表面，且不会影响飞艇内部填充气体的换热.

(2) 将飞艇内部填充气体看作完全透明气体，不考虑内部气体对辐射的吸收及发射.

未考虑蒙皮透射特性的传统飞艇热环境模型及换热机制如图1和2所示.

图1 传统平流层飞艇热环境

图2 传统飞艇热模型换热机制

然而，在实际计算中，根据蒙皮材料特性的不同，外部热源辐射会或多或少地透射穿过蒙皮，作用在内部填充气体以及对面蒙皮上.考虑蒙皮透射特性时，外部辐射经过飞艇的路径示意图如图3所示.

图3 考虑蒙皮透射特性的外部辐射路径示意图

本文在传统飞艇热特性模型的基础上，补充考虑了蒙皮的透射特性，研究了外部辐射热源对于飞艇内部填充气体热特性的影响，并计算了蒙皮与内部填充气体之间的辐射换热.本文提出的考虑蒙皮透射特性的新飞艇换热机制如图4所示.

图4 新飞艇热模型传热机制

1.2 飞艇蒙皮热力学方程

由于平流层空气稀薄，飞艇体积庞大，且外部热源在蒙皮上分布不均匀，因此同一时刻蒙皮不同处的温度差别很大，在研究飞艇蒙皮的受热情况时，不宜将蒙皮看作一个整体进行分析，本文采取分布参数法，将蒙皮表面划分成若干个三角形单元进行热特性的分析.为了在保证结果准确性的前提下提高计算效率，本文在计算飞艇传热过程时采用了如下的基本假设：

(1) 由于浮空器蒙皮只能吸收一部分热辐射而反射其余部分，所以可将蒙皮近似为灰体, 平衡状态下蒙皮材料的红外发射率与其红外吸收率相等.

(2) 由于对于一般的漫灰体，在工程上的温度变化范围内，其红外吸收率以及红外发射率与波长和温度无关，所以可假设蒙皮表面红外发射率不随波长变化；由于短波波长范围很小，所以也可以假设蒙皮表面短波辐射吸收率不随波长变化.

(3) 由于蒙皮单元的大小相较于浮空器非常小，每个单元上的温度梯度极小，所以蒙皮各单元内的温度可近似看成均匀分布.

(4) 由于本文设计的浮空器为内部被浮升气体填满的椭球体，所以可假设蒙皮内表面所有单元均为非凹面.

(5) 由于蒙皮厚度极小且导热率低，所以沿厚度方向的热传导以及不同蒙皮单元之间的热传导可以忽略不计.

考虑透射穿过蒙皮的辐射在飞艇内部反复被蒙皮及内部填充气体反射、透射及吸收的过程，为了保证计算的准确性，本文使用内部填充气体的等效物理参数来计算此换热过程中的热特性.根据文献[13]给出的等效参数计算公式，可得内部填充气体等效太阳辐射吸收率αgaseff和等效红外发射率εgaseff，计算方法如下：

(1)

(2)

式中：αgas、εgas分别为内部填充气体常态时的太阳辐射吸收率以及红外发射率；τskinsol、τskinIR分别为蒙皮对太阳辐射以及红外辐射的透射率；rskinsol、rskinIR分别为蒙皮对太阳辐射以及红外辐射的反射率.

考虑蒙皮透射率的飞艇表面蒙皮单元i的瞬态温度控制方程为

QIRSky,i+QIRin,i+QIRgas,i+Qci,i+Qco,i

(3)

式中：cskin,i、mskin,i及Tskin,i分别为蒙皮单元i的比热容、质量及温度；式右端为单位时间内蒙皮单元i上吸收的所有热量的总和，Qs,i、Qsunsa,i及Qg,i分别为太阳短波辐射中直接太阳辐射、天空散射辐射以及地面及云层反射辐射在单位时间内被飞艇蒙皮单元i吸收的热量；QIREarth,i、QIRSky,i、QIRin,i及QIRgas,i分别为长波辐射中蒙皮外表面吸收的地面长波辐射和天空长波辐射、飞艇蒙皮内表面单元之间辐射换热以及飞艇蒙皮与内部填充气体之间的辐射换热在单位时间内被飞艇蒙皮单元i吸收的热量；Qci,i、Qco,i分别为蒙皮内表面自然对流换热以及外表面混合对流换热过程中在单位时间内被飞艇蒙皮单元i吸收的热量.

飞艇表面蒙皮单元i在单位时间内吸收的直接太阳辐射量计算式为

Qs,i=λ1αskinIsAskin,icosβ1

(4)

式中：λ1为直接太阳辐射的遮挡系数，考虑蒙皮的透射率，当直接太阳辐射直接作用在蒙皮单元i上时，λ1=1，反之λ1=τskinsol(1-αgaseff)；αskin为蒙皮对太阳直射辐射的有效吸收率；Is为直接太阳辐射强度[14]，与大气透射率以及大气层外边界处的太阳辐射强度相关；Askin,i是蒙皮单元i的面积;β1为蒙皮单元法向与太阳光线的夹角.

天空散射辐射、地面及云层反射辐射、周围大气长波辐射以及地面长波辐射这4个热源的辐射方向不随时刻改变(天空散射辐射以及周围大气长波辐射的方向始终竖直向下，而地面及云层反射辐射以及地面长波辐射的方向始终竖直向上)，因此在计算蒙皮单元吸收的热量时，蒙皮遮挡系数有一定的共性.可首先根据蒙皮单元i的法向与竖直向下方向的夹角β2判断出半透明蒙皮材料飞艇表面蒙皮单元i所在位置，然后按照对应表面的热量计算式计算蒙皮单元吸收的热量.

(1) 若飞艇表面蒙皮单元在飞艇上表面，则蒙皮单元i在单位时间内吸收的天空散射辐射、周围大气长波辐射、地面及云层反射辐射以及地面长波辐射计算式如下[2,5,15-16]：

(5)

(6)

(7)

QIREarth,i=τskinsol(1-εgaseff)εskin_ex(IIREarth-

(8)

式中：Isunsa、Ig分别为天空散射辐射强度以及地面及云层反射辐射强度；σ为玻尔兹曼常数；εskin_ex为蒙皮外表面红外发射率；IIREarth和IIRSky分别为等效地球长波辐射强度以及等效大气长波辐射强度.

(2) 若飞艇表面蒙皮单元在飞艇下表面，则计算式分别为

Qsunsa,i=τskinsol(1-αgaseff)αskinIsunsa×

(9)

QIRSky,i=τskinsol(1-εgaseff)εskin_ex(IIRSky-

(10)

(11)

(12)

飞艇蒙皮内表面间的辐射换热的计算式为

(13)

式中：εskin_in为蒙皮内表面的红外发射率; 第i个单元发射的热辐射Ji可以表示为

(14)

i=1,2,…,N

Xi,j是i单元相对于j单元的角系数[17].

蒙皮内表面单元i单位时间内吸收的内部填充气体热辐射量计算式为

QIRgas,i=εskin_inIIRgasAskin,i

(15)

式中：IIRgas为内部填充气体发射的红外辐射强度.在计算内表面蒙皮与内部填充气体之间的辐射换热时，将气体及蒙皮单元等效成灰体，根据灰体辐射的四次方定律，可以得到内部填充气体发射的辐射强度为

(16)

式中:Tgas为内部填充气体的温度.

单位时间内，蒙皮单元i内表面吸收的自然对流换热量以及外表面吸收的混合对流换热量计算式分别为

Qci,i=hin(Tgas-Tskin,i)Askin,i

(17)

Qco,i=hex(Tatm-Tskin,i)Askin,i

(18)

式中：Tatm为外部大气的环境温度；hin和hex分别为飞艇内部自然对流换热系数及外部混合对流换热系数[18]，计算式如下

(19)

(20)

式中：λg为内部填充气体的热导率；D为蒙皮单元所在飞艇截面的直径；参数Cl=0.515；Ra为局部瑞利数；n为与流动特征有关的变量.由于飞艇外表面与大气既存在一定的相对运动，又有温度上的差别，因此飞艇外表面与空气之间的换热为混合对流换热，要综合考虑自然对流和强迫对流两种换热，hfree_ex及hforced_ex分别为外部自然对流及外部强迫对流换热系数，当自然对流与强迫对流同向或横向时取正值，逆向时取负值.一般情况下n取值为3，但在涉及水平平板和圆柱的横向流动时，n分别取3.5和4更为合适.本文在对飞艇热特性仿真时采用正号，n取4.

由于蒙皮外表面与大气存在一定的相对运动，需要考虑外部强迫对流换热，外表面局部强迫对流换热系数计算公式为[19-20]：

hforced_ex=

在计算飞艇外部自然对流换热时，可将飞艇按截面分成许多个微元柱进行分析，根据流动特性的不同可将换热分为层流和湍流.自然对流初期，边界层厚度远远小于飞艇截面直径，换热近似为层流传热.随着流动距离的增加，边界层厚度越来越大，与此相对应，表面传热系数越来越小.当边界层厚度达到临界值时，层流传热将转变为湍流传热，边界层厚度保持恒定，不再与流动距离相关.层流湍流的分界点对于外部自然对流换热的计算至关重要.本文流体介质为空气，其普朗特数约为 0.733 6.

图5所示为为圆柱体层流湍流转化分界点与瑞利数关系，图中：RaD为直径D处的局部瑞利数；θc为临界瑞利角度；θ为表面单元倾斜角；g为重力加速度.根据图5可得在Pr=0.72时层流湍流临界角度θc与瑞利数之间的关系，从而判断飞艇表面单元的自然对流换热是层流还是湍流.

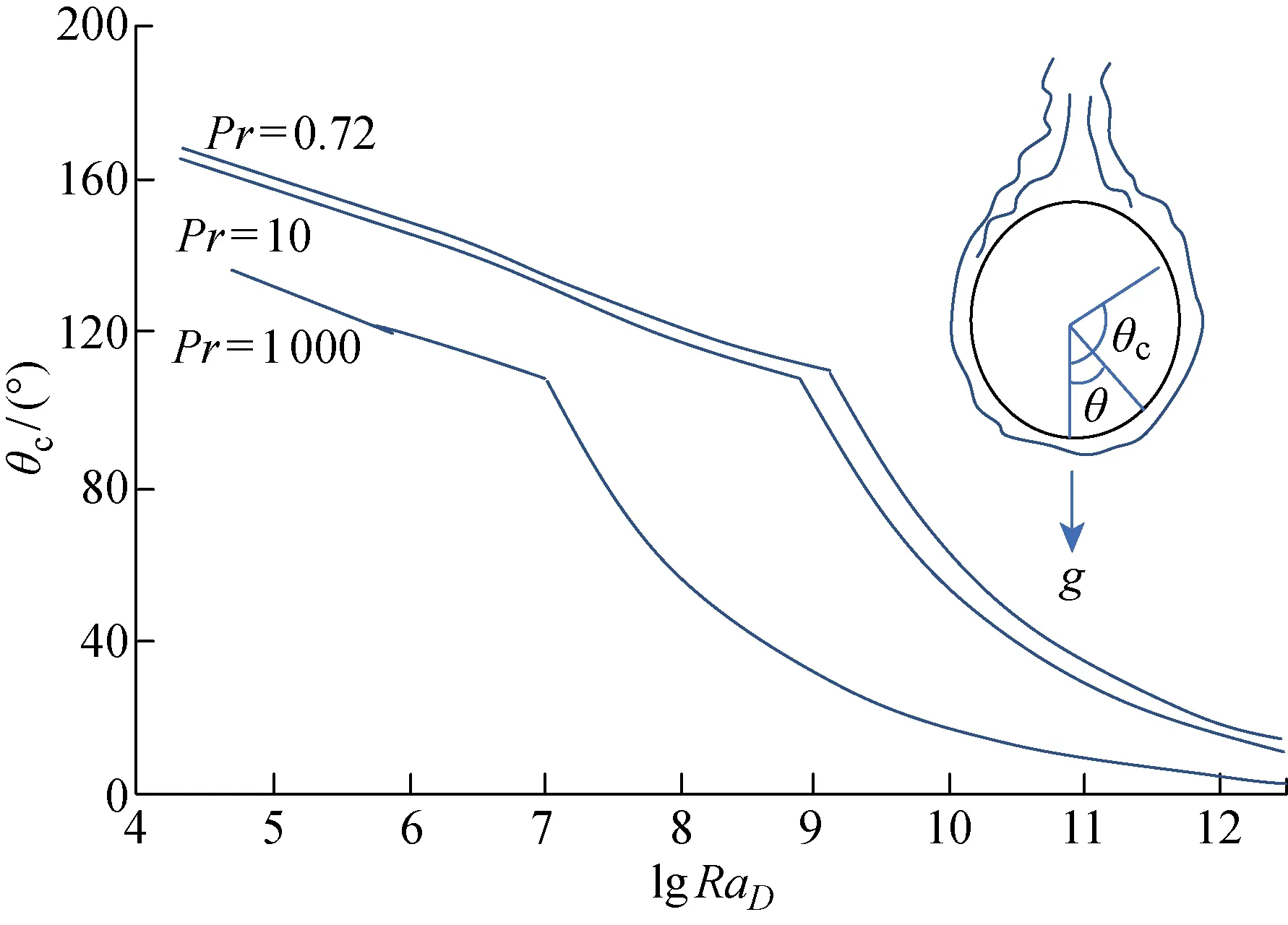
图5 圆柱体层流湍流转化分界点与瑞利数关系[21]

对直径为D的圆柱，壁面温度和来流温度均为常数，x为沿流线的距离.图6所示为飞艇外部自然对流截面参数示意图，图中：r为计算点与圆柱轴线的距离；Δl为计算点与圆柱壁面的距离.

图6 飞艇外部自然对流截面参数示意图

外部自然层流换热与湍流换热的对流换热系数以及努塞尔数的计算式如表1所示，表中：NuD为直径D处的努塞尔数；Nux为直径x处的努塞尔数；Rax为x处的局部瑞利数；kair为空气的导热系数；Cc=0.49[Pr/(0.861+Pr)]1/4;Ct=0.14Pr0.084；A(θ)是与θ有关的函数：

表1 层流及湍流对流换热系数及努塞尔数计算式

(21)

1.3 内部填充气体热力学方程

飞艇内部填充气体受太阳辐射、长波辐射以及与内表面蒙皮之间的自然对流换热的作用，因此热力学方程式可以写成：

(22)

式中：cgas、mgas及Tgas分别为内部填充气体的比热容、质量及温度；∑Qci,i为单位时间内填充气体与所有蒙皮单元自然对流换热量总量；内部填充气体在单位时间内吸收的太阳辐射总量以及长波辐射总量分别为

(23)

(24)

(25)

2 计算方法与模型验证

首先通过CFD软件建立了所设计飞艇的3D几何模型，将飞艇表面蒙皮划分成若干个三角形单元，然后采用Tecplot对单元数据进行转换，形成了MATLAB仿真程序需要的飞艇模型数据.基于上述的飞艇热力学特性的数学模型，使用MATLAB编程，实现了整个热模型的仿真.最后采用Tecplot以及Origin软件处理了计算结果，并对结果进行了一系列的分析.

2.1 时间步长及网格对计算结果的影响分析

本文数值仿真的计算程序中，有蒙皮单元以及时间两个离散量.为在保证计算结果的准确性的前提下提高计算的效率，分析了蒙皮网格数与时间步长对飞艇热特性计算的影响.以两个昼夜(48 h)内的飞艇热特性变化为1个算例，初始计算参数如表2所示，填充气体为He.

表2 算例基本输入参数

分别计算了不同时间步长dt以及不同表面网格数Nm下的飞艇蒙皮及内部填充气体的热特性.图7所示为不同表面网格数的直观网格剖分图.内部填充氦气温度以及蒙皮最高超热温度随时刻的变化分别如图8和9所示.图中：Tmax为蒙皮最高温度；Tmin为蒙皮最低温度；t为实验总时间.

图7 不同表面网格数的直观网格剖分图

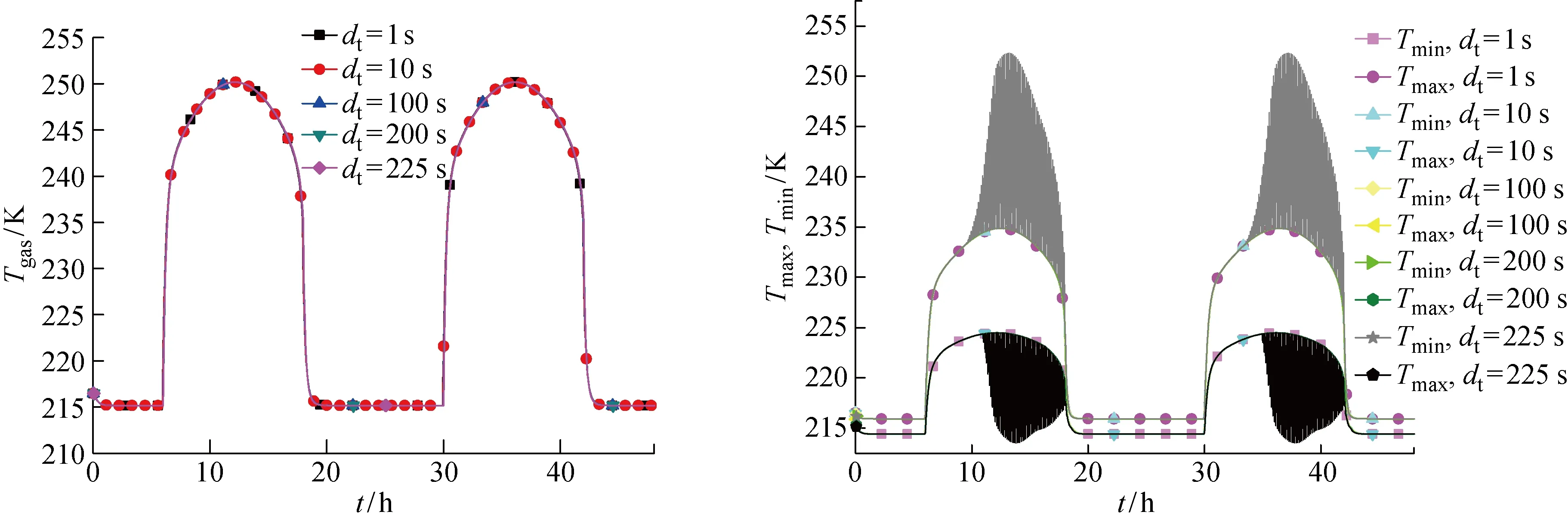
图8 不同时间步长下飞艇热特性48 h内的变化

由此可知，当时间步长在200 s以内时，时间步长对飞艇表面蒙皮以及内部填充气体热特性没有影响，但当时间步长达到225 s时， 内部填充He的温度与其余时间步长下的计算值有了细微偏差，位于He最高温度右侧，且蒙皮最高超热温度在白天也开始出现了振荡， 可以判断225 s的时间步长对于计算模型来说过大，会导致计算结果不准确.而不同网格数对填充气体的热特性基本无影响，对蒙皮温度的影响也很小，最大温度偏差为0.7 K.

图9 不同网格数下飞艇热特性48 h内的变化

因此，本文在之后的计算中采用200 s作为计算的时间步长，采用 4 666 作为计算的网格数，既能保证计算结果的准确性，也能提高计算效率.

2.2 模型验证与结果分析

为了验证本文飞艇热特性模型、计算程序及方法的准确性，针对文献[16]中的实验进行了仿真，并将数值计算结果与文献中的实验结果进行对比分析.文献[16]模型实验通过太阳模拟器模拟太阳辐射，通过环绕在飞艇表面及内部的18个铜-康铜热电偶采集蒙皮和内部气体的温度，并用风机以及引气道控制飞艇的外部对流环境.具体实验参数见表3.

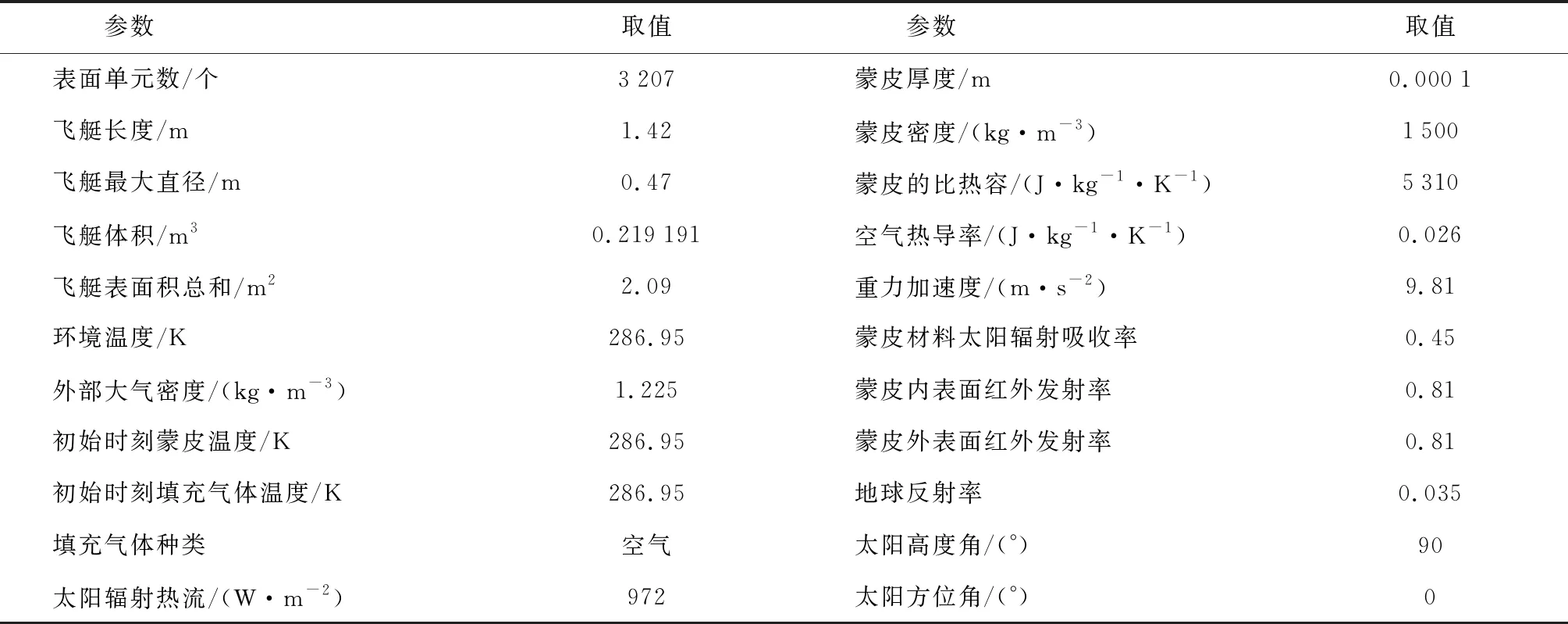
表3 文献[16]实验基本几何参数

从图10中可知，数值计算出的飞艇内部空气温度的平均值在17，18号传感器测量的空气温度值之间，与测量值吻合较好且变化趋势基本相同.

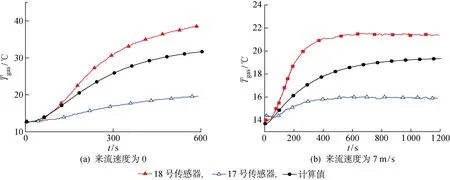
图10 内部填充气体平均温度的计算值与实验值对比

来流速度为0，计算时间为300 s时，由实验测得的上部填充气体温度(18号传感器30.7 ℃)及下部填充气体温度(17号传感器17.0 ℃)，可得填充气体平均温度实验值为23.9 ℃，而填充气体平均温度计算值为25.7 ℃，比填充气体平均温度的实验值高1.8 ℃，相差7.5%.计算时间为 600 s 时，由实验测量得到的上部及下部填充气体温度(18号传感器 38.7 ℃，17号传感器19.6 ℃)，可得填充气体平均温度实验值为29.2 ℃，而填充气体平均温度计算值为31.6 ℃，比填充气体平均温度实验值高 2.4 ℃，相差8.2%.

当来流速度为7 m/s，计算时间为600 s时，实验测量得到的上部及下部填充气体温度分别为21.3 ℃和16.0 ℃， 因此填充气体平均温度实验值为18.7 ℃，而填充气体平均温度计算值为18.6 ℃，比填充气体平均温度实验值低0.1 ℃，相差0.5%.计算时间为 1 200 s时，实验测量得到的上部及下部填充气体温度分别为21.3 ℃及15.9 ℃，填充气体平均温度实验值为18.6 ℃，填充气体平均温度计算值为19.3 ℃，比填充气体平均温度的实验值高出 0.7 ℃，相差3.8%.

考虑到文献[16]模拟实验中，太阳模拟器的误差约为±5%，风速仪的误差约为±2%，热电偶的测量误差约为±1%，再综合考虑实验中存在的其他环境与人员操作误差，可认为数值计算的结果与实验结果较好地吻合.

3 飞艇热力学特性分析

本文研究了基于相关参考文献确定了一些可靠的初始输入参数[13,16].蒙皮材料的热辐射特性如表4所示.其余具体初始输入参数如表2所示.

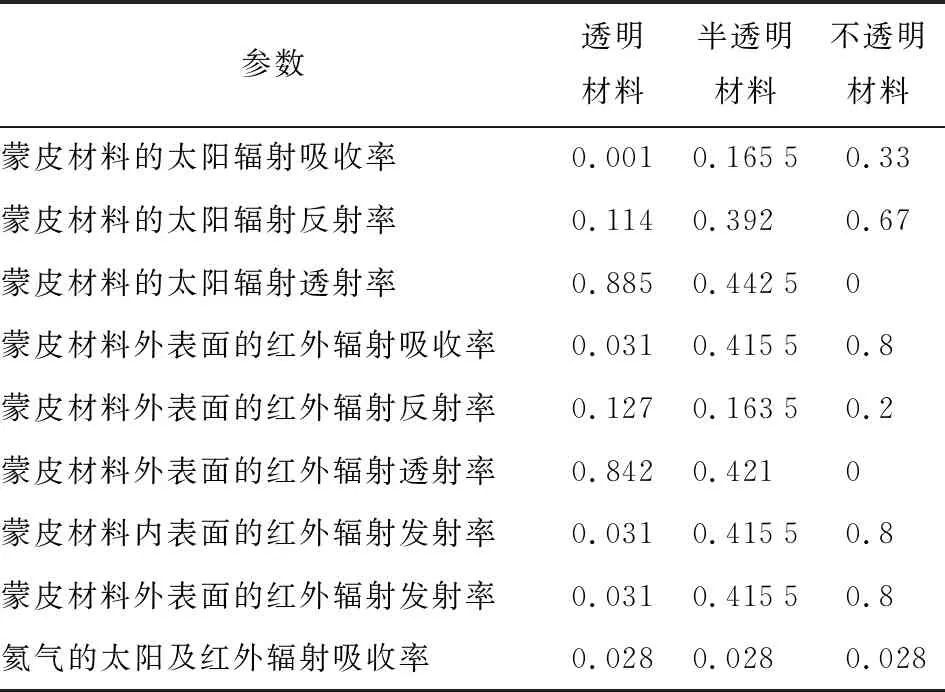
表4 蒙皮材料热辐射特性

飞艇囊体的超冷超热特性是蒙皮自身以及内部气体热辐射特性综合作用的结果，通过图11和12给出的3种典型材料下飞艇内部He和外蒙皮温度变化可知，透明材料因其具有低的吸收率和高透射率，可使飞艇囊体内部He和蒙皮的超冷超热量均低于半透明材料及不透明材料，是更加理想的飞艇蒙皮材料. 考虑材料的透射特性以及内部填充气体对辐射的吸收与发射特性，能够更加准确地获得飞艇内部气体及蒙皮的温度范围.

图11 不同蒙皮材料的飞艇内部填充气体温度48 h内的变化

图12 不同蒙皮材料的飞艇蒙皮最高温度48 h内的变化

4 结语

平流层飞艇在驻空期间的热特性会影响其浮力、蒙皮应力及整艇变形，浮力的变化和囊体变形引起的整艇阻力的显著变化会对飞艇的飞行性能产生显著的影响，故准确的飞艇热模型及其热特性分析成为其关键技术之一.

本文在已有研究的基础上，根据常用飞艇蒙皮材料以及内部填充气体的特性，将蒙皮的透射特性和内部填充气体对辐射吸收与发射特性这两方面的因素进行考虑，推导出飞艇表面蒙皮及内部填充气体的热力学方程.基于有限拆分法建立了考虑蒙皮透射率的飞艇热力学仿真模型，并对其求解精度进行了验证.

最终基于典型蒙皮材料的热辐射特性，给出飞艇填充气体及外蒙皮的热特性及其变化规律，可为飞艇设计以及驻空期间的飞行性能评估提供参考和指导.