储能汇聚参与辅助调频服务的协同优化算法

曾 君,胡家健 ,徐铭康,潘志伟,刘俊峰

(1.华南理工大学电力学院,广东广州 510640;2.华南理工大学自动化科学与工程学院,广东广州 510640)

1 引言

储能即能量的储存,它实现了能量传输在时间和空间上的解耦,是促进能源生产消费开放共享和灵活交易,实现多能协同,推动电力体制改革和促进能源新业态发展的核心基础.随着以可再生能源为代表的分布式能源的蓬勃发展,用户侧分布式储能将成为储能的重要形式.以电化学储能为主要形式的用户侧储能,具有快速功率调节特性,能有效提高分布式能源尤其是可再生能源发电的消纳率,减少电网对大规模集中储能的依赖,将是未来电力市场的重要组成部分.

从分布式储能配备的情况来看,储能多以“备用”形态出现.以微电网为例,综观目前商业化运行或者示范性微电网储能与可再生能源的配比多在2:1以上[1–2].即便是在较低配比情况下,从储能24小时荷电状态和充放电功率曲线来看[3–5],在有效的能量管理策略下,储能大部分时间处于闲置状态.因此,有研究者提出:在配电网中引导分布式储能汇聚形成规模效应,汇聚可观的储能容量,用以参与电网调峰、调频、调压等辅助服务,是一种崭新的思路[6–7].这样可以充分提高分布式储能的资产利用率,提高储能的经济性.

为汇聚一定区域内的分布式储能形成规模效应,除政策和市场机制等因素外,从技术的角度来看,还有以下关键问题:

1) 分布式储能汇聚的是储能的“闲余”容量,其参与辅助服务的时段碎片化.将碎片化容量聚合起来形成类似于集中式储能的集体,为电网提供辅助服务.这是汇聚的根本.但如何解决碎片化所带来的随机性,是难点所在.

2) 分布式储能的本地控制系统计算资源和信息存储资源均十分有限,在分布式储能汇聚过程中,需尽可能极小化分布式储能之间的通信量,同时减少储能本地控制系统的计算量.

因此,有效的协同机制是分布式汇聚参与电网辅助服务的关键.本文从储能所具有的快速功率调节特性着手,以分布式储能汇聚参与一次调频辅助服务为例展开研究.目前,电网辅助服务中储能调频技术较为成熟.国内外已有多个储能调频项目陆续实施.学术界在该领域的研究也已十分深入[9–13].但是,这些成果中大多以大容量集中式储能作为研究对象.相关研究成果并不完全适用于用户侧分布式储能.有鉴于此,本文提出了一种适用于分布式储能汇聚调频的协同优化算法.

该算法首先基于状态势博弈理论[14],将参与汇聚的分布式储能个体映射为局中人,基于分布式储能对电网一次调频的效用构建了分布式储能的价值函数,将分布式储能汇聚参与调频辅助服务问题转化为状态势博弈问题,完成基本建模.进一步,在极小化通信量和计算量的原则下,本文建立了分布式储能的行为逻辑与互动机制,使得在分布式储能个体退出调频响应时,剩余分布式储能可通过相互博弈来动态调整自身策略,逐步增大自身利益,并保证分布式储能集群单位调节功率的充足与稳定.

本文的特色在于:1)所提出的协同优化算法以高效汇聚分布式储能冗余容量,为电网调频辅助服务提供稳定的单位调节功率为目标.它是分布式储能个体在原有用途基础之上的“复用”,相比传统储能调频采用的“专用”集中式储能,是对已有资源的进一步利用,且能够实现储能用户与电网的双方共赢;2)所设计的博弈机制能适应分布式储能因自身原有用途而固有的随机接入特性,可引导分布式储能有序参与调频辅助服务;3)所提出的协同优化算法为完全分布式算法,在系统初始化后无需中心机构的引导,也无需更新全局信息.符合分布式储能天然具有的“分布式”和“自主性”特性,便于实施.

2 系统介绍与理论基础

2.1 分布式储能调频机理分析

虚拟惯性控制与虚拟下垂控制是储能参与调频的两种经典控制策略,对于电网频率工况均有改善作用.其中虚拟惯性控制策略能抑制频率变化率,虚拟下垂控制策略能够减小稳态频率偏差[11].

当储能采取虚拟下垂控制策略时,其在一次调频中的作用如图1所示,其中(a)(b)分别对应负荷加重、负荷减轻两种状况,黑色曲线表示传统机组的静态功频特性,灰色曲线表示计及储能调频作用的系统整体静态功频特性.不难看出,采用虚拟下垂控制策略的储能可改善系统静态功频特性,在相同的负荷扰动作用下,能有效减小系统稳态频率的偏移.

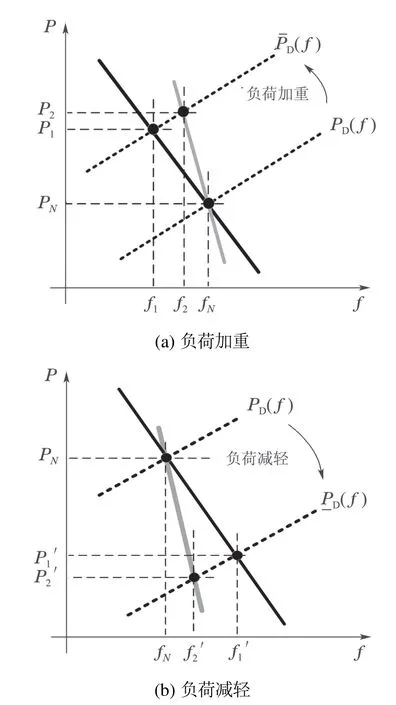
图1 针对频率偏差进行一次调频Fig.1 Primary frequency modulation for frequency deviation

当系统中参与调频辅助服务的储能由集中式的单一储能变为分布式储能时,储能所执行的虚拟下垂控制策略仍可如图1所示,改善系统的静态功频特性.相应地,在系统一次调频动态模型中,表征储能调频作用的反馈环节变为多个,如图2虚线框所示.

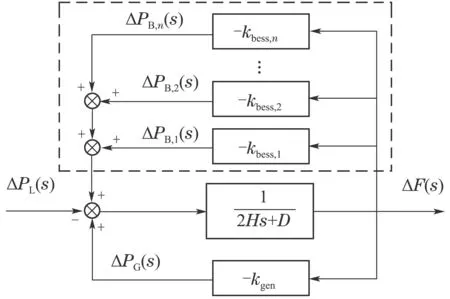
图2 含多个储能的一次调频动态模型Fig.2 Dynamic model of primary frequency modulation with multiple energy storages

图2中,kbess,1,kbess,2,kbess,3,···,kbess,n表示参与调频辅助服务的各储能单位调节功率;kgen表示传统发电机组的单位调节功率;∆PB,1(s),∆PB,2(s),···,∆PB,n(s)表示各储能出力变化;∆PG(s)表示传统机组的出力变化;∆F(s)表示频率偏差;H为系统旋转惯量;D为系统阻尼系数.

因此,从机理上而言,分布式储能同样可以参与到电网调频辅助服务中,达到与大规模集中式储能相同的控制效果.难点在于:1)分布式储能的随机性.分布式储能的形式多样,不同类型的储能装置因其配置目的和应用场景的不同拥有不同的可参与电网辅助调频时段,具体表现为其投入和退出调频辅助服务的时刻均会存在差异.在机理上反映为储能闭环控制环节的反馈环的频繁断开或增添,系统单位调节功率之和∑kbess,i将会不断波动,系统频率偏差存在超出允许范围的风险;2)分布式储能调频时效性.传统电力系统的一次调频主要通过发电机的调速器进行,响应时间一般在10 s内.为达到合格的调频效果,分布式储能调频的响应速度应与之持平.综上所述,设计能够兼顾时效性的分布式储能协同优化机制是关键.

因此,本文以维持系统整体单位调节功率充足和稳定为控制目标,即:

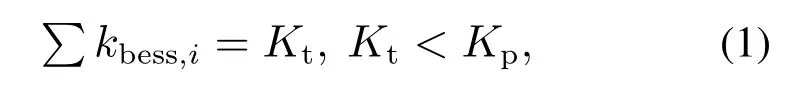
其中:Kt为分布式储能集群汇聚的目标单位调节功率,Kp为由前期分析得到的对分布式储能集群在调频辅助服务中可提供的最大单位调节功率的估计.后者可通过蒙特卡洛方法或曲线拟合方法对分布式储能功率特性进行分析得到,国内外也已有类似的研究[15–16].以此为基础,后文将从分布式储能汇聚建模、分布式协同方法交互机制设计等方面入手,提出一套完整的方法解决前述难点.

2.2 基于多代理系统的分布式储能汇聚调频建模

本文基于多代理系统(multi-agent system MAS)技术建立一定区域内的分布式储能集群汇聚模型.如图3所示.在该区域内,各分布式储能个体映射为节点Agent,并假设各Agent具备:1)与邻近节点通信功能;2)一定的数据存储、处理功能;3)本地频率测量、功率控制功能.

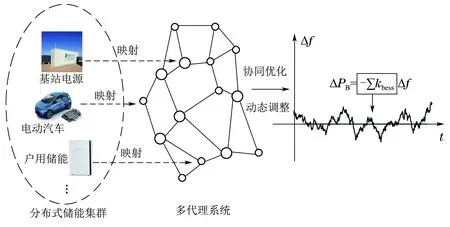
图3 基于多代理系统的分布式储能调频系统Fig.3 Distributed energy storage frequency modulation system based on multi-agent system

节点Agent可通过相互博弈实时调整自身单位调节功率,同时可根据图2所示动态模型与实测频率偏差调整自身出力.在此基础上,本文建立了分布式储能汇聚协同机制.考虑到汇聚过程是一个离散连续的混合过程,本文以事件驱动机制触发,即以储能个体退出调频响应为触发事件,使得整个系统从连续运行过程转入协同优化决策过程,完成系统内各节点Agent单位调节功率{kbess,i|i ∈1,2,···}的再优化,从而跟踪控制目标式(1).

该离散决策过程实际上是在分布式储能个体已知自我冗余容量,且集群总汇聚容量受限情况下的多个体博弈过程.在设计该博弈机制过程中,需考虑如下关键问题:

1) 一次调频用于调整变化幅度小,变化周期短的负荷波动(一般为10 s以内)带来的频率偏移[17],当触发事件发生后,优化需要在数秒内完成.

2) 由于所研究的分布式储能集群数量大,且频繁接入/退出调频辅助服务,难以建立中心机构进行管理.所设计的博弈机制应当是一种具备自适应能力的完全分布式优化机制,在运行过程中无需任何全局信息.

3) 分布式储能在能量存储、功率输出等方面根据类型用途不同有较大差异,应根据分布式储能对电网一次调频的效用构建分布式储能的价值函数.

3 博弈机制

3.1 状态势博弈理论基础

状态势博弈[14]在势博弈[18]的基础上,在博弈环境中引入辅助分布式决策的状态空间,拓展为状态型博弈.该方法又可视作类随机博弈的一种简化型,尤为适合于主体间具有耦合约束的分布式优化问题.

3.1.1 状态势博弈的定义

(确定型)状态势博弈G={N,{Ai},{Ji},X,f}的博弈要素如下:

1) 局中人N={1,2,3,4,5,···,n};

2) 状态空间集X;

3) 对于任意分布式个体i ∈N,对应的状态x ∈X,均有状态相关行动集Ai(x);

4) 对于任意分布式个体i ∈N,状态x ∈X以及联合行动集,均有状态相关成本函数Ji(x,a);

5) (确定型)状态转移函数f(x,a)∈X,其中x ∈X,a ∈A(x).

定义1称具有空行动集(即a=0)的(确定型)状态博弈为(确定型)状态势博弈,若存在一个(全局)势函数φ:X ×A →R,且对于任意x ∈X满足以下两种特性:

1) 对于任意博弈参与者i ∈N,行动集a ∈A(x)以及行动,均有:

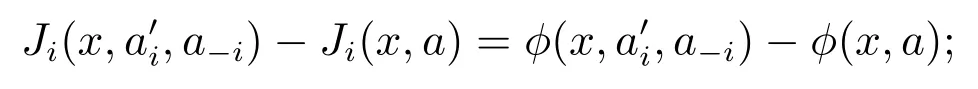
2) 对于任意行动集a ∈A(x)及继发状态→x=f(x,a),势函数φ满足:

与普通势博弈相同,在状态势博弈中,特性1要求任意博弈参与者效益函数值的增量等于势函数值的增量.特性2描述了势函数沿状态轨迹的变化特性.

定义2称一个状态动作对(x∗,a∗)为状态势博弈的静态纳什均衡,若

1) 对于任意博弈参与者i ∈N,均有

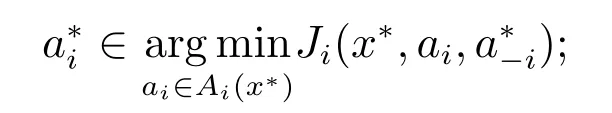
2) 状态点x∗是状态转移函数的一个固定点,即

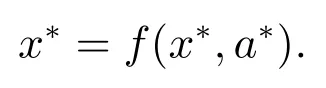
3.1.2 状态势博弈的属性

属性1:当状态势博弈的势函数收敛至最优时,各主体的效益函数同样收敛至最优.

属性2:有限序数势博弈都有纯策略的均衡解.

属性3:有限序数状态势博弈具有有限改进特性.

因此,有限序数状态势博弈必然存在静态纳什均衡,只需在建模过程中构造状态势博弈,即可保证模型是收敛的.

3.2 博弈机制设计

3.2.1 问题描述

分布式储能作为一种调频资源其价值有高低之分,高储电量、高功率储能具有更高的利用价值.为衡量分布式储能在一次调频中的价值,同时使得优质储能在本文设计的调频机制中具有比较竞争优势,定义第i个储能对电网的价值函数如下:

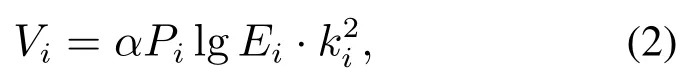
因此,所研究的分布式储能汇聚参与一次调频优化问题可表述如下:

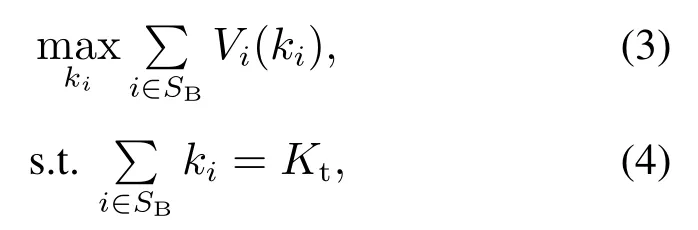
其中SB表示由分布式储能构成的集合.

下文将基于状态势博弈理论的5种要素:局中人、状态空间、行动集、效益函数及状态转移函数,将上述问题转化为状态势博弈,使得分布式储能集群可通过所设计的博弈机制形成汇聚效应,提供持续稳定的调频辅助服务.

3.2.2 局中人

在所述的分布式储能调频系统中,各储能能够自主决策自身在储能调频辅助服务中的参与深度及参与时段,故将其映射为局中人.

目前,国内外针对储能调频的补偿大多为调频里程补偿,与储能参与调频的深度直接相关.而在本文所设计的博弈机制中,储能尝试提高自身对电网的价值,其实质同样是尝试提高自身的调频参与深度.故此,在本文中储能追逐自身效益最大化与促进系统效益最优是方向一致的.

对于一个具有完全理性的储能i,其总是尝试提高自身单位调节功率ki以提高自身价值Vi(ki),同时尽可能利用闲余时间及闲余容量参与调频辅助服务,仅在以下情形退出响应:

1) 因储能原本用途而退出.如电动汽车出行需求、光伏储能储电需求等;

2) 因储电量过低而退出.

3.2.3 状态空间

对于所有局中人构成的集合SB中的任意个体i ∈SB,其状态空间包含策略变量ki及越限估计量{ei}两种状态变量.

1) 策略变量.

ki为储能i的单位调节功率,与电网实时频率偏差共同决定储能在调频辅助服务中的出力变化,除满足式(4)所示的全局耦合约束外,还应满足本地约束

其中:第1项约束为功率约束,∆Fdev为系统最大允许频率偏差;第2项约束反映了储能虚拟下垂控制策略要求.由于储能电量不足可自主退出响应,故本地约束中不考虑荷电状态.

2) 越限估计量.

等式约束(4)可拆解为不等式约束

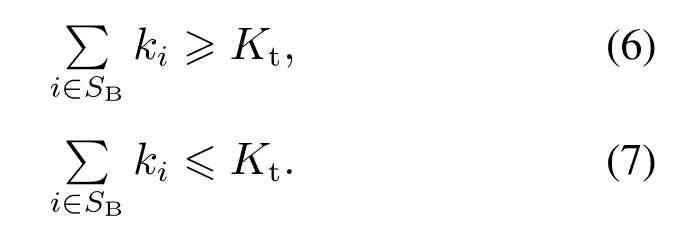
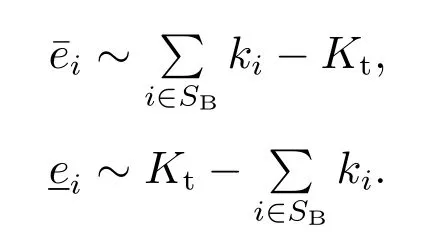
3.2.4 行动集

定义集合Ni为储能i的邻域,包含与储能i通过信道直接连接的所有储能(一般地,可取为以分布式储能i为圆心的圆形区域内的所有其他储能个体).则储能i的行动集元素可表示为

3.2.5 效益函数

为确保所设计状态型博弈为一状态势博弈,本文参考文献[19],使用添加外部罚函数的方法构造储能i的效益函数Ji(x,a)及全局势函数Φ(x,a):

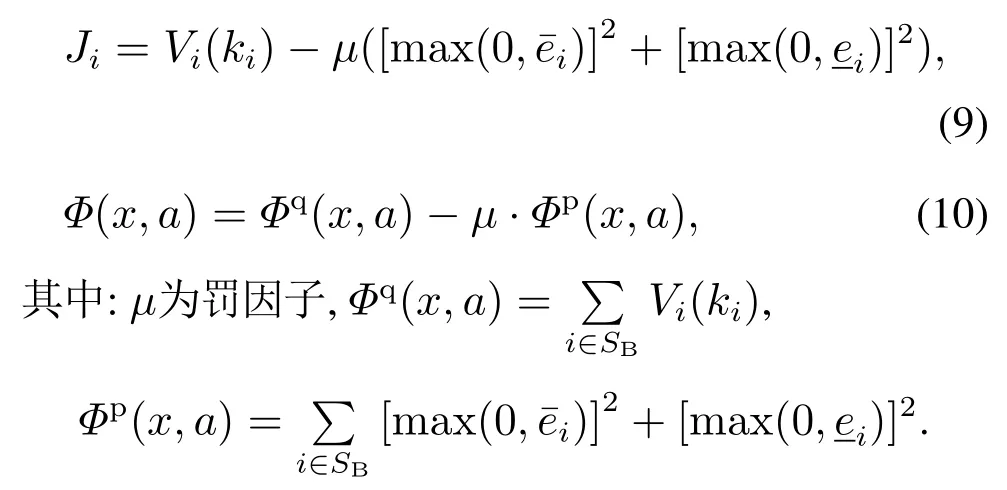
不难证明,所构造的效益函数Ji(x,a)及全局势函数Φ(x,a)满足前文所述关于状态势博弈的定义.

3.2.6 状态转移函数

状态转移函数描述了状态势博弈中续发状态与前一状态的关系,通过不断执行状态转移函数修改策略变量ki及越限估计量,局中人策略被不断优化的同时,全局耦合约束亦得到更好的遵守.

令状态转移函数如下:

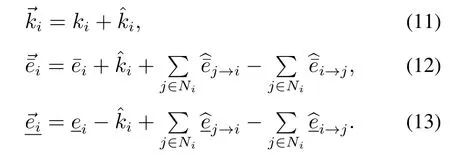
对于状态势博弈,有多种主体学习算法可保证收敛,考虑一次调频对时效性的要求,保证算法收敛速度,由梯度下降算法原理,令

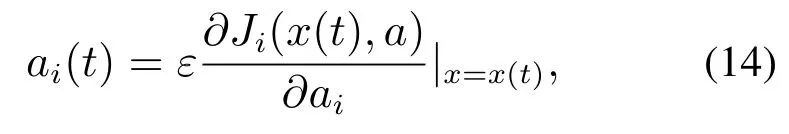
即

另外需要指出的是,由于迭代步长ε及罚因子µ与局中人效益函数直接相关,需将其设置为不可更改的全局变量以避免损害局中人利益.

4 基于事件触发机制的响应过程

如图4所示,在分布式储能集群的协同优化过程中,前述的博弈机制将因触发事件的发生而启动,引起系统内各节点Agent单位调节功率{ki|i ∈SB}的再优化,维持全局单位调节功率∑ki的稳定.其中,触发事件指分布式储能退出调频响应的情形.

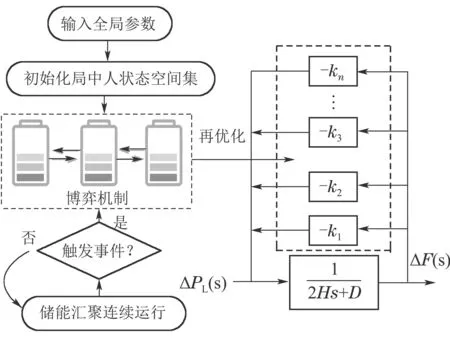
图4 基于事件触发机制的响应过程Fig.4 Collaborative optimization algorithm based on event triggering strategy

4.1 算法初始化

协同优化算法的初始化包括以下步骤:

步骤1对于∀i ∈SB,输入全局参数,包括初始响应节点数目N、罚因子µ、迭代步长ε、越限估计量精度ξ、修正系数α、分布式储能集群目标单位调节功率Kt.

步骤2对于∀i ∈SB,节点i根据本地约束(5)随机选取单位调节功率初始值ki(0),并依照式(18)–(19)初始化越限估计量.

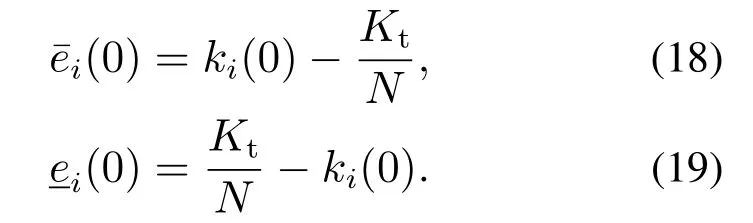
步骤3对于∀i ∈SB,节点i分别根据式(11)–(13)(15)(17)更新状态空间及动作量.若e¯i≤ξ,停止更新策略变量ki.

其中对于步骤2,根据式(18)–(19),可知

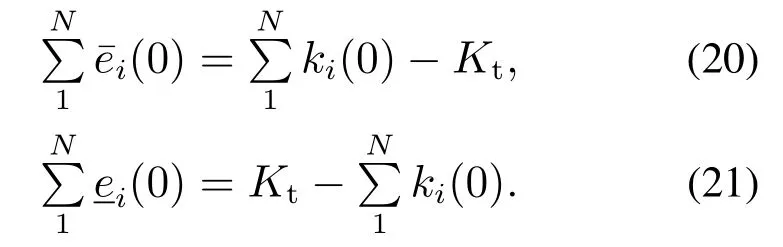
而由式(16)–(17)的对称性可知,节点之间动作量的交换仅造成越限估计量在相邻储能之间转移,而并不改变越限估计量的总和,即有

4.2 事件触发机制及响应过程

理论上讲,分布式储能加入或退出都会导致系统单位调节功率变化,应当将二者均作为协同优化的触发事件.但在实际过程中由于在新储能个体加入响应之前,其余储能已经通过博弈机制达成纳什均衡,系统单位调节功率已经充足,没有必要进行触发博弈.如图5(b)所示,新加入的储能个体暂时并不投入到调频响应中,而仅作为系统热备用.当部分分布式储能由于原有用途退出响应引起系统单位调节功率不足时(如图5(c)所示),充当热备用的储能才会通过博弈机制获得单位调节功率份额,实际参与一次调频响应.

1) 储能加入调频辅助服务.

假设在时刻t之前,系统满足全局约束(4),单位调节功率充足.在时刻t,储能i希望加入调频辅助服务,需经过以下步骤:

步骤1节点i将状态空间置零.

步骤2节点i向邻域节点j ∈Ni发送加入响应请求,使节点j开始计算与节点i的动作交换量,节点i成为调频响应热备用.

2) 储能退出调频辅助服务.

假设在时刻t之前,系统满足全局约束(4),单位调节功率充足.如图6所示,在时刻t储能i退出调频辅助服务将引起系统单位调节功率不足,触发博弈机制以补足单位调节功率.

具体来说,节点i退出调频响应遵循以下步骤:

值得说明的是,在节点i退出调频响应过程中,节点i通过动作交换量将由于自身退出响应所引起的越限估计量变化传递到邻域节点j ∈Ni的越限估计量及.即在储能退出调频响应过程中,仍只发生了越限估计量在各储能之间的转移,式(22)(23)依然成立.

另外,从节点i退出调频响应到全局约束(4)再次被满足期间,无须任何额外全局信息.

5 算例验证

如图7所示,本文以一个含可再生能源的交流微电网为例,验证所提出协同优化算法的有效性.其中,假设该微电网额定负荷为2 MW,系统旋转惯量H=10由采用虚拟惯性策略的储能机组提供;D为系统阻尼系数=0.75.

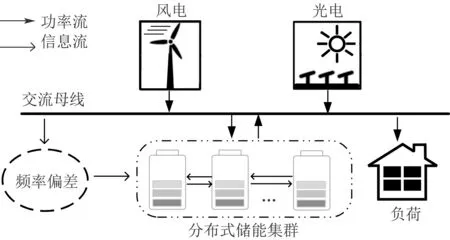
图7 微电网中的分布式储能汇聚模型Fig.7 Distributed energy storage aggregation model in microgrid

12 min系统荷扰动及因此引起的频率偏差分别如图8–9所示.

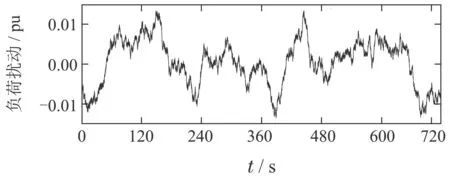
图8 12 min负荷扰动变化曲线Fig.8 12 min continuous load disturbance curve

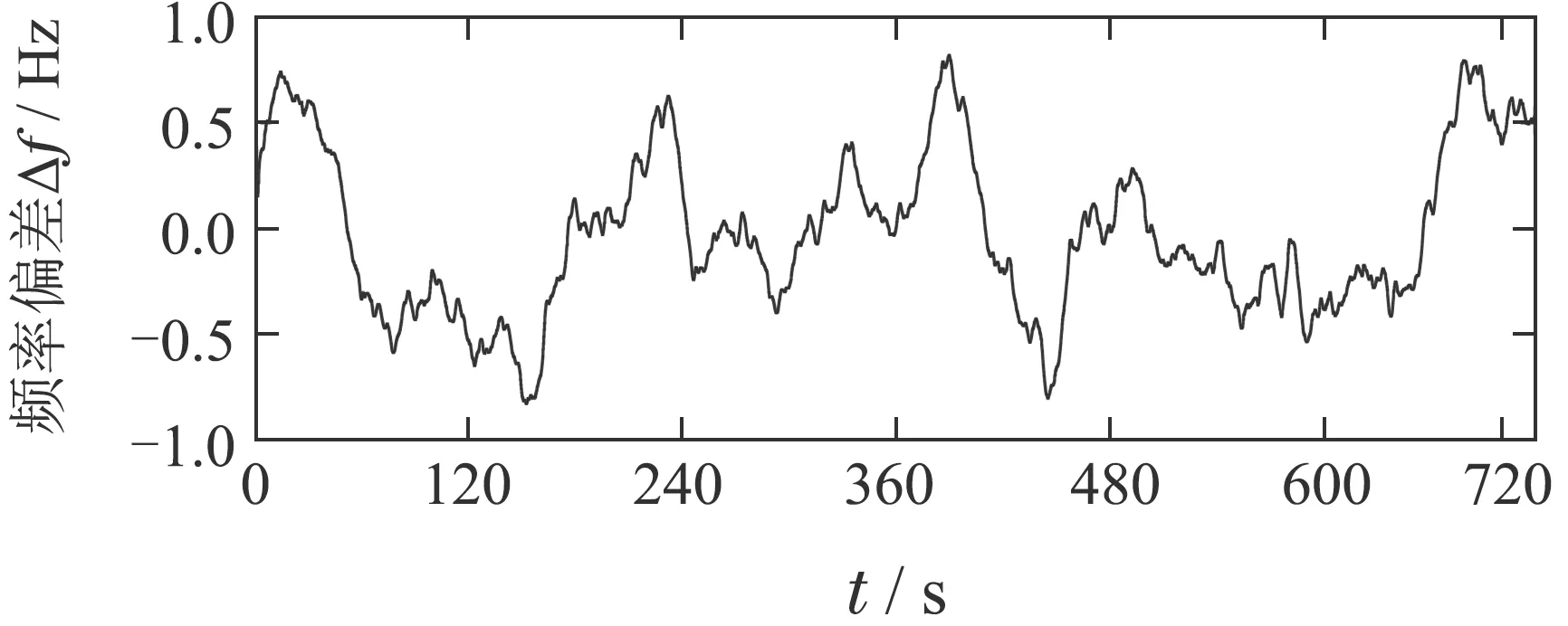
图9 12 min频率波动变化曲线Fig.9 Frequency variation under 12 min continuous load disturbance

5.1 分布式储能集群一次调频性能分析

参考文献[11],系统稳态频率偏差与单位调频功率的关系如下:

其中:∆Fvoss为稳态频率偏差;∆PL为负荷扰动;为采取虚拟下垂控制策略的储能的单位调节功率,在本文中.

取系统最大允许频率偏差|∆Fdev|=0.5 Hz,同时由图8可得系统最大负荷扰动为0.015 pu,则为使系统频率限制在允许范围内,需要大于0.75,考虑裕量,需引入(有名值)的一次调频电源.

假设在该微电网中,有20个分布式储能可参与一次调频辅助服务,其主要参数如表1所示.

以上述20个分布式储能构成储能调频系统,基于本文所提出的协同优化算法对该微电网提供调频辅助服务.取全局参数罚因子µ=10;迭代步长ε=0.005;越限估计量精度ξ=0.1、修正系数α=0.05、分布式储能集群目标单位调节功率Kt=40 kW/Hz(假设该分布式储能集群能提供足够的单位调节功率).由于储能状态空间变量迭代规则简单,可忽略其执行时间,状态量的更新间隔主要受限于通信延迟.本文假设储能状态空间的更新时间步长为0.1 s.

利用MATLAB/Simulink搭建如图10所示动态模型.

图10中,调频死区选为±0.033 Hz.为实现变参数传递,反馈环节参数由代码模拟分布式储能集群的博弈机制后,通过Simulink/S-Function模块传入.

为模拟分布式储能集群的随机特性,在12 min的仿真过程中考虑以下情形:

1)t1=100 s,储能5退出响应;

2)t2=250 s,储能5加入响应;

3)t3=400 s,储能9退出响应;

4)t4=600 s,储能13退出响应.

如图11所示,从整体来看,在分布式储能参与一次调频辅助服务后,交流微网内频率偏差被缩小到最大允许频率偏差范围内.

图11 分布式储能集群参与调频效果图Fig.11 Effect of distributed energy storage cluster participating in frequency modulation

下面就算法效果进行进一步分析.

如图12所示,算法初始化后,t1,t3,t4时刻储能的退出将使得∑ki幅值出现瞬态跌落,但在本文博弈机制的作用下,剩余响应储能将快速进行单位调节功率的调整,使得∑ki幅值快速回升.整体来看,算法能有效跟踪所设置的分布式储能集群目标单位调节功率Kt.从快速性而言,算法响应速度也能达到一次调频的时效要求.

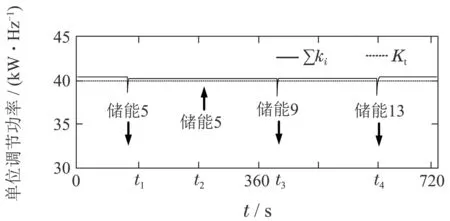
图12 算法跟踪目标单位调节功率效果图Fig.12 The tracking effect of proposed algorithm

进一步的,为研究本文算法作用下的分布式储能集群与具有稳定单位调节功率集中式储能在调频效果上的差异,构建如图13所示模型.

图13中,除反馈环节替换为稳定参数外,其余参数同分布式储能调频情形.将由此得到的频率偏差与分布式储能集群调频得到的频率偏差作比较后得到图14.

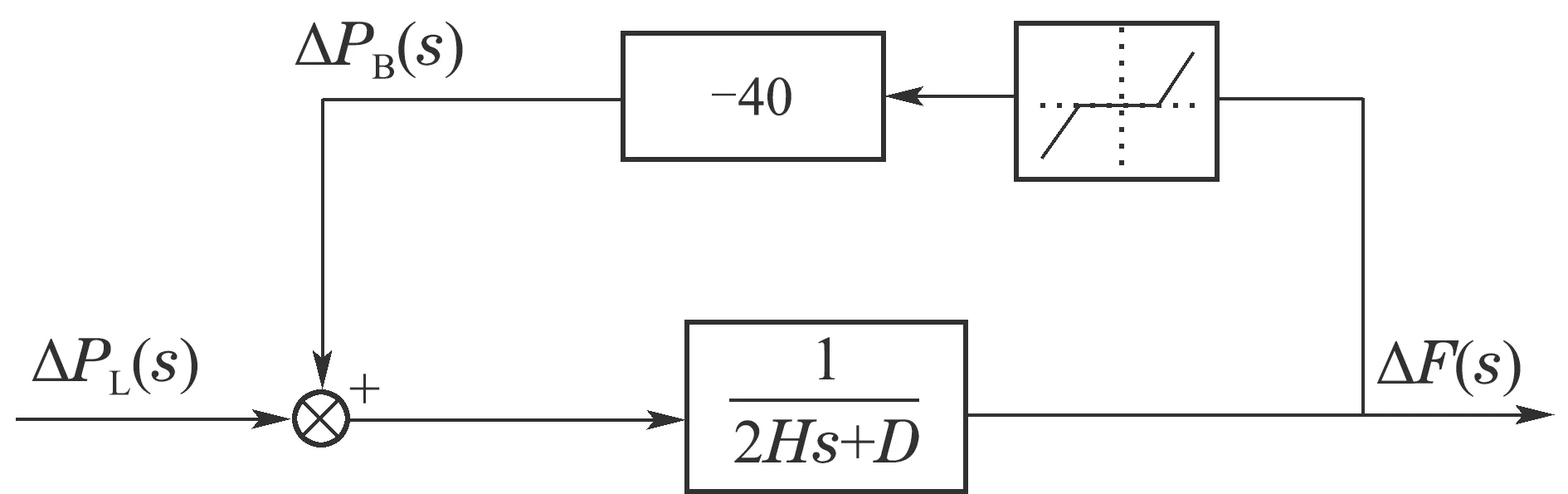
图13 集中式储能调频动态模型Fig.13 Dynamic model of Centralized energy storage in primary frequency modulation

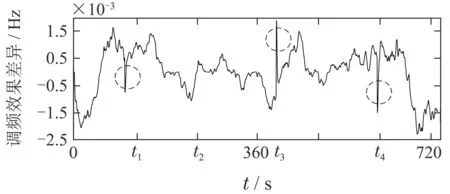
图14 调频效果差异曲线图Fig.14 The difference between two kinds of storages in primary frequency modulation

如图14,由于正值稳态误差的存在,采用两种不同调频电源,仅在调频效果差异曲线中引起与负荷扰动相关的微小差异,但并非实质性差异(小于0.002 Hz).

另外,虽然t1,t3,t4时刻储能的退出将引起数倍于稳态误差ess的单位调节功率缺额,但由于该缺额所引起的变化十分短暂,在系统一阶惯性环节的低通滤波作用下,该变化在调频效果差异曲线中仅表现为毛刺尖峰(如图14虚线框所示).

总的来说,在本文所提出的协同优化算法作用下,分布式储能集群可有效跟踪所设定的目标单位调节功率Kt,且在一次调频中的作用与具有稳定参数的集中式储能基本一致.

5.2 分布式储能效益分析

为更好地向各分布式储能提供策略指导,本文进一步分析储能在协同优化过程中的策略变化.

在上述的仿真试验中,将具有典型特性的储能5策略变化情况单独绘出如图15所示.储能5在t1时刻退出调频辅助服务;在t2时刻重新参与调频辅助服务时,由于系统已处于稳态,其单位调节功率暂时仍为0.但随着t3,t4时刻储能9和储能13退出引起单位调节功率缺额,储能5通过博弈机制,逐步增大自身单位调节功率,提升自身收益(单位调节功率决定储能在调频辅助服务中的参与深度,从而决定实际调频份额).

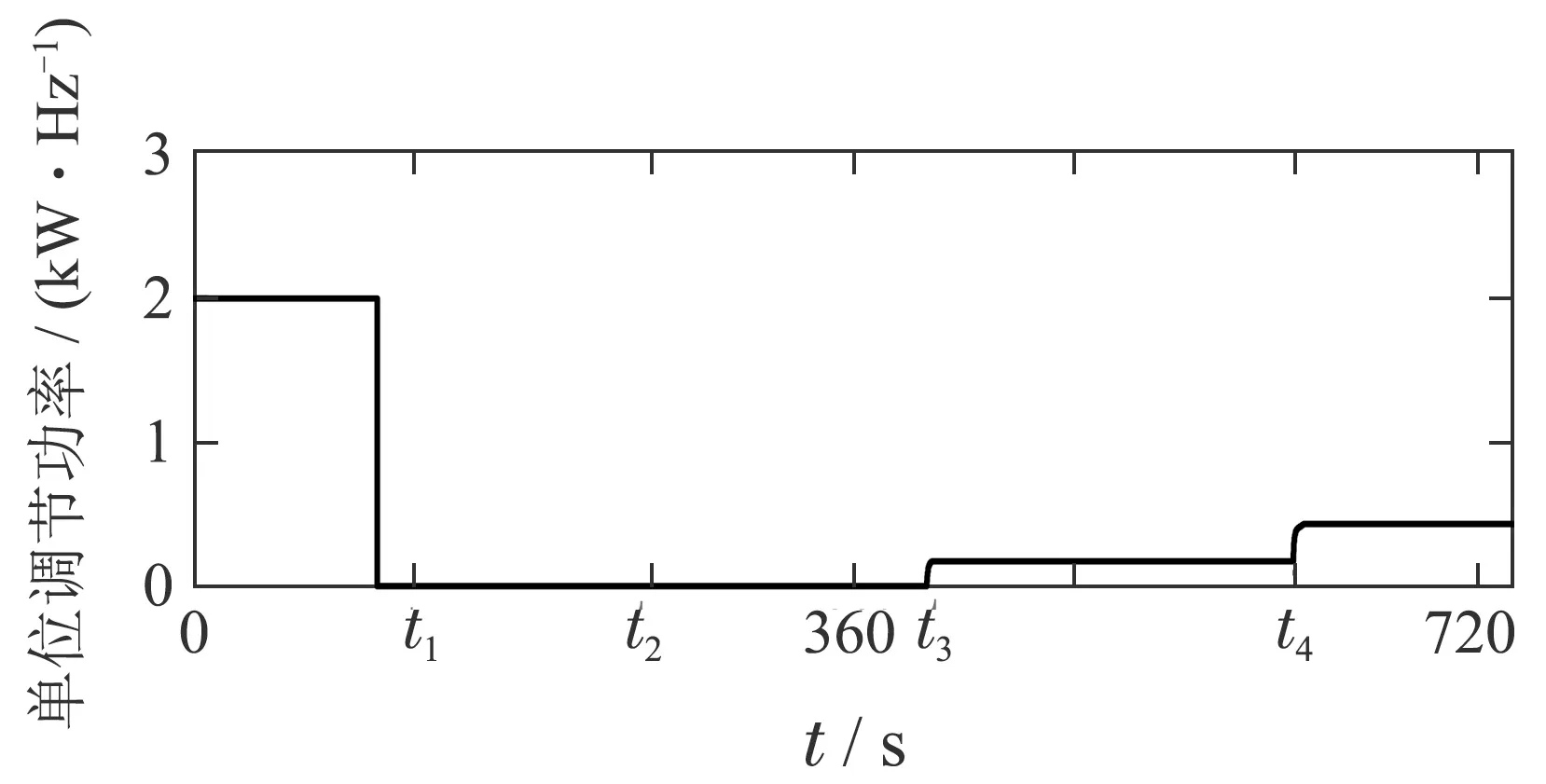
图15 储能5策略变化曲线图Fig.15 The strategy curve of storage 5

这反映了在本文所设计的储能调频系统中,储能的实际收益不仅与功率上限、储电量多少有关,更与储能参与时长有关.因此,对于具有完全理性的储能节点Agent,其将尽可能延长参与调频辅助服务时间,同时减少退出调频辅助服务的次数.显然,该种特性又将反过来减少全局单位调节功率的扰动,提高储能调频系统的稳定性.

6 结论

广泛分布在用户侧的分布式储能系统存在相当规模的闲余时间和闲余容量,且由于用途种类各异,各储能个体间存在互补性.本文基于状态势博弈理论在分布式储能集群中引入博弈机制,设计协同优化算法,使得分布式储能集群可通过相互博弈维持单位调节功率充足和稳定,为电网提供持续稳定的一次调频辅助服务.该算法为完全分布式优化算法,在运行过程中无需任何全局参数,且计算量小,对计算资源要求低,可实现各储能之间通信量的极小化,同时保证了算法的高效性.