环形直流微电网的二次控制与稳定性分析

刘骁康,王燕舞,肖江文

(华中科技大学人工智能与自动化学院,湖北武汉 430074;华中科学大学图像信息处理与智能控制教育部重点实验室,湖北武汉 430074)

1 引言

近年来,直流微电网系统的控制与优化问题备受关注[1].与传统的交流系统相比,直流系统传输效率高且安全可靠,同时能够较好地接纳风、光等分布式可再生能源.直流微电网的发展不仅推动着传统电力系统结构的转型,同时也在电网智能化和市场化的道路上扮演着重要角色[2].

电流分配和电压调控是直流微电网的两个基本控制目标[3].由于直流微网中的转换器仅能工作在电压控制模式或电流控制模式,因此无法同时调节单个节点的输出电压和输出电流.从系统控制的角度来看,这是一个控制维度为1但目标维度为2的问题[4].为实现电流分配,早期研究者们采用了虚拟阻抗法[5],其中V–I下垂控制方法广为流行.值得一提,下垂控制是一类经典的分散式控制方法,无需通信且实施简单.通过设置下垂系数即可实现电流分配[7–9].但由于线路阻抗和固有的下垂行为,电流分配和电压调控都存在稳态误差.为消除稳态误差,研究者们进一步设计了补偿器.微电网系统中存在着多时间尺度现象,它是一类典型的奇异摄动系统[6].充分考虑时间尺度特性,研究者们提出了分层控制框架[7–9].该框架包含了一次、二次和三次控制.其中,下垂控制为一次控制,补偿器为二次控制.借助通信网络技术,研究者们基于多智能体系统的一致性算法设计了各式各样的分布式二次控制器.此举不仅能够增强系统的鲁棒性,还能够提高调控时的精度.综合网络化诱导因素和控制性能,研究者们进一步提出了计及通信时滞的二次控制[10]、基于牵制控制的二次控制方法[11]、有限时间二次控制方法[13]、事件驱动的二次控制方法[12]、混杂二次控制方法[14]等.

目前绝大多数的分布式二次控制器仅适用于单总线的直流微电网系统.然而,在一些实际应用中,直流微电网采用了多总线和环形总线的结构,这使得已有的面向单总线系统的控制器设计和稳定性分析方法不再适用.此外,相比于单总线,采用环状总线更有利于线路故障的检测与保护[15].因此,环形结构也常用于飞机、轮船的直流供电系统[16].值得一提,环形直流微电网与多总线直流微电网的电压调控目标相似,即期望总线的平均电压维持在额定电压值,如文献[17–19].尽管多总线直流微电网二次控制器的设计方法可以在环形总线系统上得到应用,但在分析环形结构时,需对分布式能源节点和负载节点进行划分.文献[20]系统地研究了环形微电网,采用动态下垂系数的方法解决了负载分配控制问题,并进一步基于小信号模型方法建立了稳定性判据.然而,在线路阻抗未知的情况下,仅改变下垂控制系数的方法仍然会使系统调控时存在稳态误差,且采用小信号模型仅能够得到局部稳定的结果.此外,在现有文献中,针对多总线系统和环形直流微电网系统的稳定性分析工具多采用频域下的经典控制方法,如波特图、根轨迹分析等.基于时域和状态空间的方法相较匮乏.基于此,本文从时域状态空间的角度出发,针对环形直流微电网系统提供了一种新的稳定性分析思路.

经上述讨论,本文主要贡献如下:1)针对环形直流微电网系统的二次控制问题提出了时域状态空间下矩阵特征值扰动的稳定性分析方法;2)相比小信号模型分析方法,该方法能够保证全局稳定性,同时也适用于单总线直流微电网系统二次控制问题的稳定性分析;3)最后,测试了所设计的控制算法在即插即用和并网环境下的有效性.

本文结构安排如下:第2部分提出环形直流微电网电流分配和电压调控的问题描述;第3部分给出二次控制的设计与稳定性分析;第4部分展示直流微电网的仿真算例并验证理论结果;第5部分对本文工作进行总结与展望.

2 问题描述

2.1 环形直流微电网

考虑环形直流微电网如图1所示,环形总线通过AC–DC或DC–DC转换器将分布式发电设备、储能、负载相连.不失一般性,假设环形直流微电网中有N+M个节点,其中包含N个分布式能源(发电和储能)节点以及M个负载节点.为方便表示,按照逆时针顺序标记数字并记为集合I={1,2,···,N+M}.在环形总线上,节点i处的电压和注入电流分别记为Vi和Ii,并记环形直流微电网输电线路的电导矩阵Y=[Yij]∈R(N+M)×(N+M)为

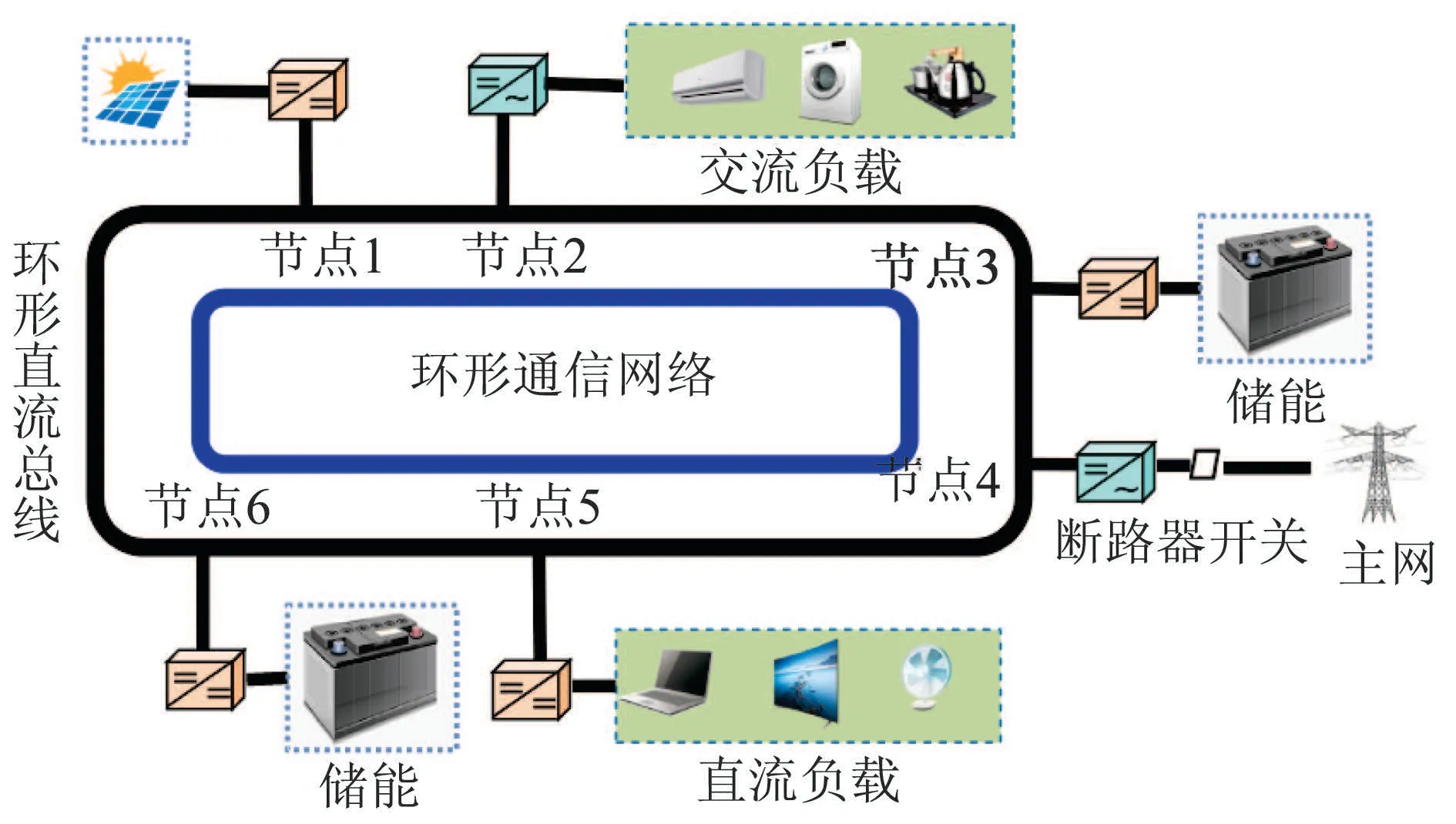
图1 环形直流微电网Fig.1 Ring-bus DC microgrid

2.2 潮流约束与通信拓扑

记I=[I1I2··· IN+M]T为节点注入电流组成的向量,且V=[V1V2··· VN+M]T为转换器输出电压组成的向量,则满足直流微电网的潮流方程

注意到分布式能源节点和负载节点的编号相互交错.为进一步单独讨论分布式能源的控制与分析,本文引入正交矩阵Ts∈R(N+M)×(N+M)来划分分布式能源节点和负载节点,

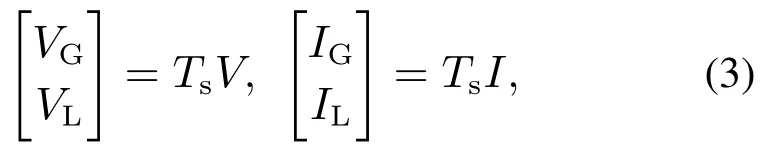
其中:VG∈RN和IG∈RN表示分布式能源节点电压和注入电流,VL∈RM和IL∈RM表示负载节点的电压和注入电流.本质上,线性变化矩阵Ts的功能是对节点的重新标记和排序.为方便分析和理解,本文将分布式能源节点和负载节点重新分开标记,并分别记为IG和IL.

由于负载节点属于无源节点,所以节点的外部注入电流为0.那么在矩阵Ts作用下,潮流方程(2)则可改写为

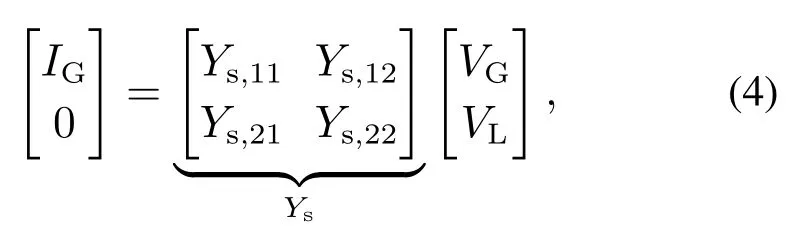
环形直流微电网通过专用通信网络来实现节点间的信息传输与交互.该通信网络可由代数图论来描述,记为G=(IG,E,A).其中:IG表示图中节点的集合,E表示节点之间连通的边,A=[aij]表示邻接矩阵.当第i个分布式能源可获取第j个分布式能源的信息时,则有aij=1,否则aij=0.若对任意i,j ∈IG满足aij=aji,则称G是一个无向图.若无向图G中的任意两个节点可在E中找到一条链路连接,则称无向图G是一个连通图.定义通信网络G的拉普拉斯矩阵L=[lij]∈RN×N如下:

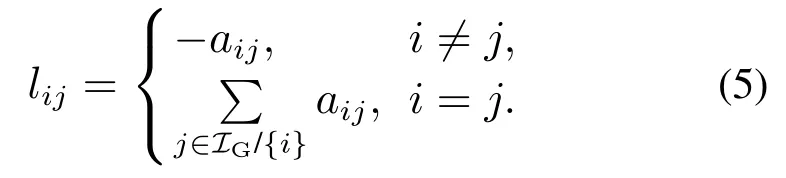
针对上述环形直流微电网系统的物理拓扑和通信拓扑,给出如下相关引理.

引理1矩阵Y,Ys,Ys,11和Ys,22都是正定矩阵.

证根据定义(1),可知Y是对称的且对角占优的方阵,从而Y的所有特征根皆为正,因此Y是正定矩阵.由于且Ts是正交矩阵,则矩阵Ys依旧保持了矩阵Y的对称性和所有特征根是正实数的特性,因此Ys也是正定矩阵.此外,Ys的对角占优性质同时保证了Ys,11和Ys,22也是对角占优的正定阵.

引理2矩阵正定.

证根据Schur补引理[21]直接得证.

引理3[22]当通信拓扑G是无向连通图时,矩阵L具有一个零特征根且其余特征根都为正.

2.3 电压调控与电流分配

本文旨在通过控制电源侧的转换器来实现微电网的电压调控和电流分配.保证分布式能源节点的平均值达到额定电压值,同时确保分布式能源节点的注入电流按照预定比例进行分配,即实现

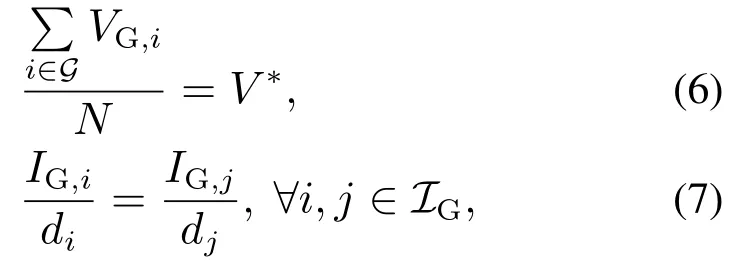
其中:V ∗为期望的额定电压值,di >0为第i个分布式能源节点注入电流的期望比例系数.

在孤岛运行时,转换器通常工作在电压控制模式.根据分层控制框架,一次控制采用电流环和电压环的双PI反馈控制.此时,分布式能源节点处转换器输出电压的工作点是可设置的,即提供给一次控制的参考信号是可调控的.设计工作点为

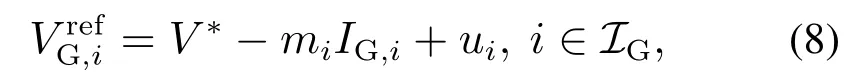
其中:mi是V–I下垂控制系数,ui是二次控制信号.为补偿一次控制的稳态误差,二次控制采用了动态反馈控制结构,其数学描述如下:

其中:δi为控制器状态,vi为待设计的控制律,i ∈IG.由于二次控制相对于转换器的动力学处于慢时间尺度,则在慢尺度下分析时,可视转换器的输出电压等于参考信号,即.式(8)可改写为

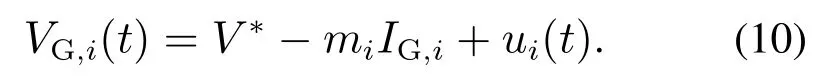
注1转换器的动力学主要由电路拓扑中的电感和电容组成.以常见的DC/DC升压电路的动力学模型为例[23],

其中:Vs为转换器输入电压,vC为输出电压,iL为电感电流,R和P为阻抗负载和恒功率负载,ud为占空比,C和L分别为电容值和电感值.直流微电网的容量较小,电感和电容的选取处于10−3H和10−3F数量级.因此,转换器控制的时间尺度处于10−2s.而二次控制的时间尺度处于1 s,如式(9)所示.因此,直流微电网是一个典型的奇异摄动系统.在分析慢时间尺度动力学时,则可忽略快尺度的动态变化.

假设分布式能源节点间的通信拓扑G是一个无向连通图.本文目标是设计分布式二次控制器(9)中的控制律vi,在代数约束(4)和(10)下,使得分布式能源节点电压和注入电流渐近收敛到控制目标(6)和(7).

3 控制器设计与稳定性分析

由于分布式控制器无法获取所有节点的电压信息,因此无法直接计算所有分布式能源节点的平均电压值.为解决该问题,本文引入分布式观测器来估计平均电压,其中观测器状态定义为,i ∈IG.在设计控制器前,首先定义3个电压误差变量

其中:表示节点i的观测状态对额定电压值的误差,表示节点i的观测误差,表示平均电压对额定电压值的误差.上述3个误差变量满足

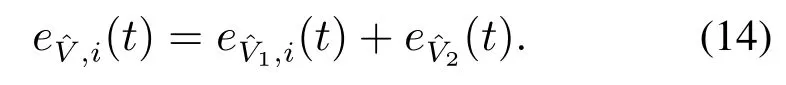
接着定义电流误差如下:

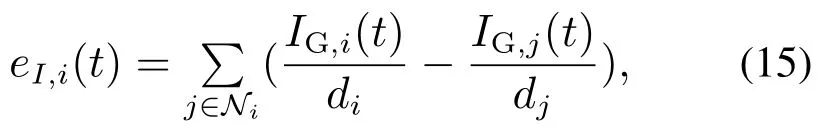
其中Ni表示第i个节点在通信拓扑G中的邻居集合.

根据定义的误差变量,设计第i个节点的分布式控制器如下:

其中α1>0和α2>0为两个待设计的控制增益,设置观测器初值为.

注2由于分布式控制器无法获取所有节点的电压信息,因此和无法用于控制信号的设计.此处定义两个误差变量便于理解其物理含义.当时,则表示节点i观测到电压平均值.当时,则表示电压平均值达到额定电压值,即实现了控制目标(6).此外,控制器(16)是分布式的,仅需邻居的观测器状态和电流信息IG,j(t).

注3实施中,式(16)的观测量可用积分形式表示[17],即.两种形式本质上相同.

3.1 闭环系统

综合式(9)(10)(16)和式(17)得到

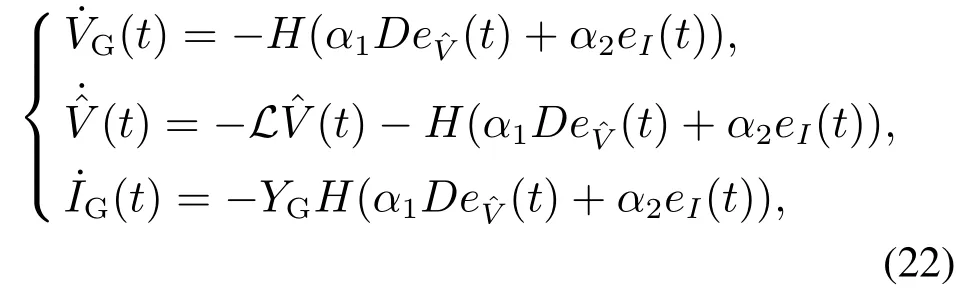
其中:H=(E+MYG)−1,M=diag{m1,···,mN},D=diag{d1,d2,···,dN},E为合适维度下的单位矩阵.值得一提,根据Woodbury formula,可得

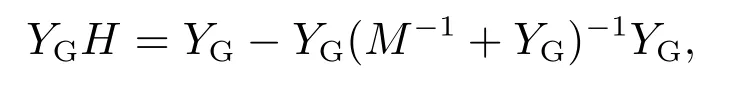
因此矩阵YGH是一个正定矩阵.

根据式(22),可进一步得到

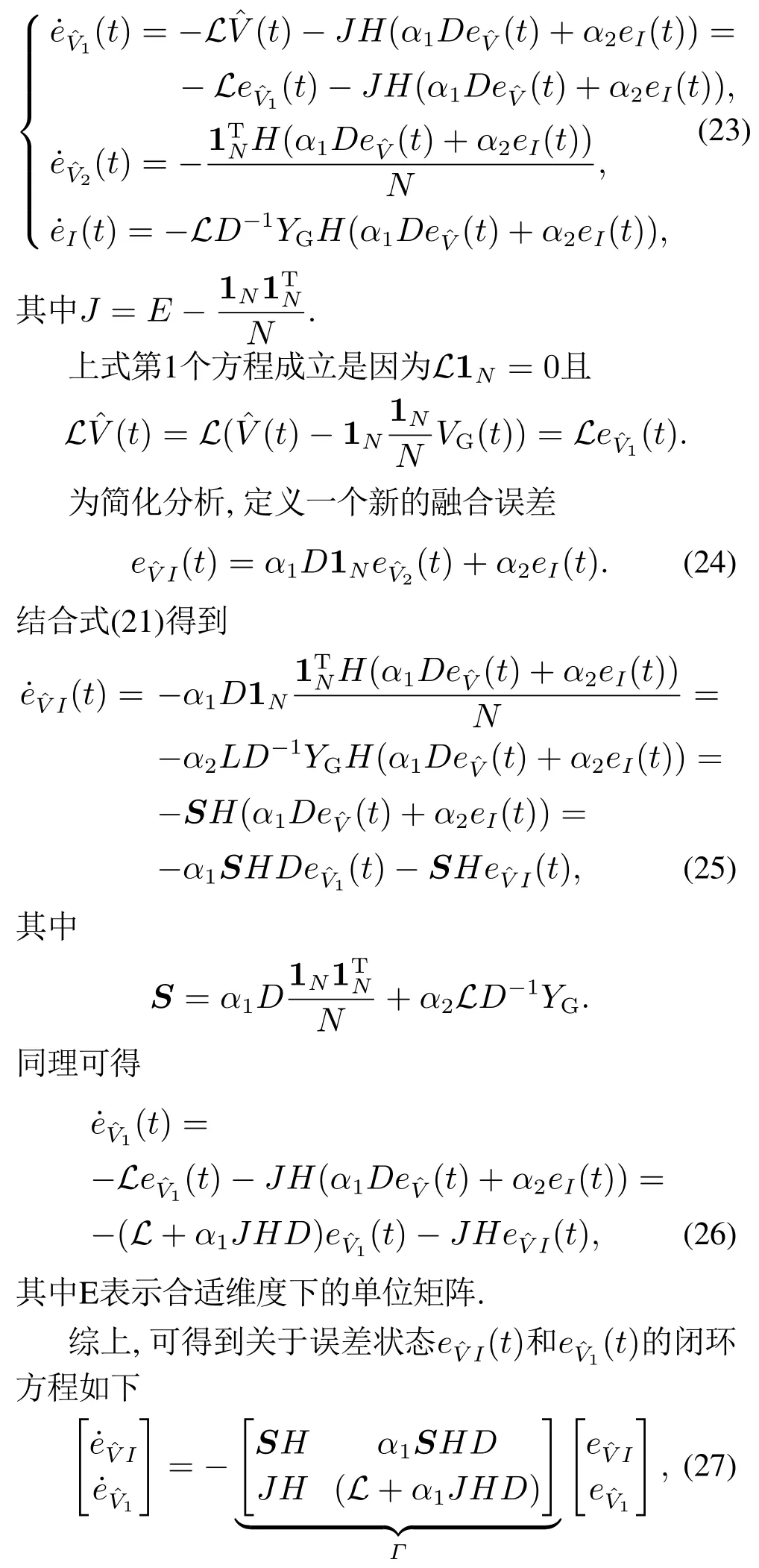
其中Γ为误差系统的动力学矩阵.值得一提,矩阵[−Γ]并非Hurwitz矩阵.为分析误差系统解的性质,需进一步对矩阵Γ的特征根与特征向量展开分析.

3.2 稳定性分析

本节首先给出两个相关引理及证明.然后,给出实现环形直流微电网电压调控和电流分配的定理条件.最后,探讨满足定理条件的控制器参数设计方法.

引理4矩阵S和矩阵SH的特征根均大于0.

证毕.

注4矩阵S及其类似形式常在单总线直流微电网中出现,例如文献[11]中的式(26).相比采用Lyapunov方法得到的条件,引理4对控制器参数的限制更弱,且无需获取系统先验知识,即对任意α1>0,α2>0,[−S]是Hurwitz矩阵.

引理5矩阵Γ仅存在唯一零特征根,且其特征向量为

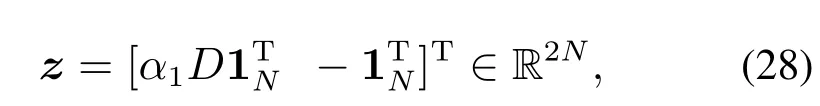
存在α1>0,使得矩阵Γ的所有特征根非负.

证首先证明对任意α1>0,Γ存在唯一零特征根.根据Guttman rank additivity formula[21](第14页),

rank(Γ)=rank(SH)+rank([Γ/(SH)]),(29)

其中[Γ/(SH)]为(SH)关于Γ的Schur补矩阵,经计算[Γ/(SH)]=(L+α1JHD)−JH(SH)−1α1SHD,代入到式(29)得到

对两组的并发症发生情况进行观察，包括压疮、感染以及肺炎等，并且记录两组的护理满意度评分、术后血糖控制时间以及切口愈合时间。

rank(Γ)=rank(SH)+rank(L)=2N −1.

由此得证Γ ∈R2N×2N仅存在唯一的零特征根.此外,可验证z是零特征根对应的特征向量,如下所示:

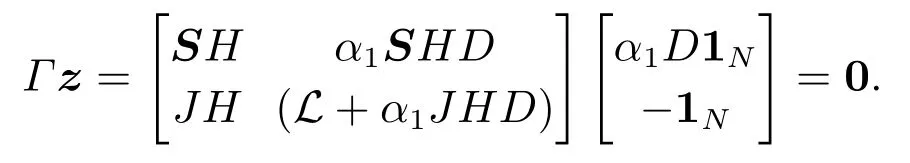
接下来根据特征根的连续性,进一步证明存在α1>0使得矩阵Γ所有特征非负.将矩阵Γ拆分为

则该问题转换为α1∆对矩阵Γ1特征根的扰动分析.由引理3和引理4,可知Γ1具有一个零特征根且其余特征根皆为正实数.当α1从0连续增大时,零特征根则始终保持不变,而其他特征根随着α1相应地连续变化.根据连续性性质可知必存在α∗,对任意α1<α∗,矩阵Γ的特征根非负. 证毕.

定理1若α1满足Γ特征根非负,则分布式二级控制器(16)能够实现环形直流微电网的电压调控(6)和电流分配(7).

证由引理5知,存在α1>0使得Γ特征根非负,且Γ存在唯一的零特征根.当Γ特征根非负时,根据线性系统理论,闭环系统(27)的解最终会收敛到线性生成空间span(z),其中z是零特征根的特征向量.

则存在标量c ∈R满足

注5在引理4、引理5和定理1的条件中,需选择控制器参数α1使得矩阵Γ所有特征根非负.引理5证明了α1的存在性,在选取的时候可通过选取相对小的α1来满足Γ特征根非负的条件.此外,定理条件对参数α2的选取要求相对宽松,仅需在控制器设计中保证α2>0即可.

4 仿真

本节采用MATLAB/Simulink仿真软件,搭建环形直流微电网测试平台,并验证所设计的二次控制器的有效性.该测试系统由4个分布式能源节点和2个负载节点组成,其拓扑结构如图2所示.每个分布式能源节点由一个额定电压为50 V的直流源和储能设备组成,并通过一个半桥结构的双向Buck-Boost转换器接入环形总线.借助通信网络,控制器可以交互信息.直流系统总线上的额定电压为100 V,其他参数详见表1.

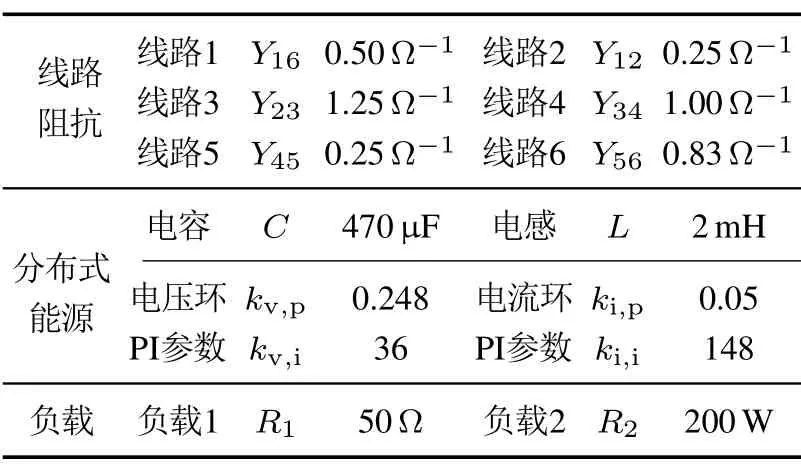
表1 环形直流微电网的参数Table 1 Parameters of ring-bus DC microgrid

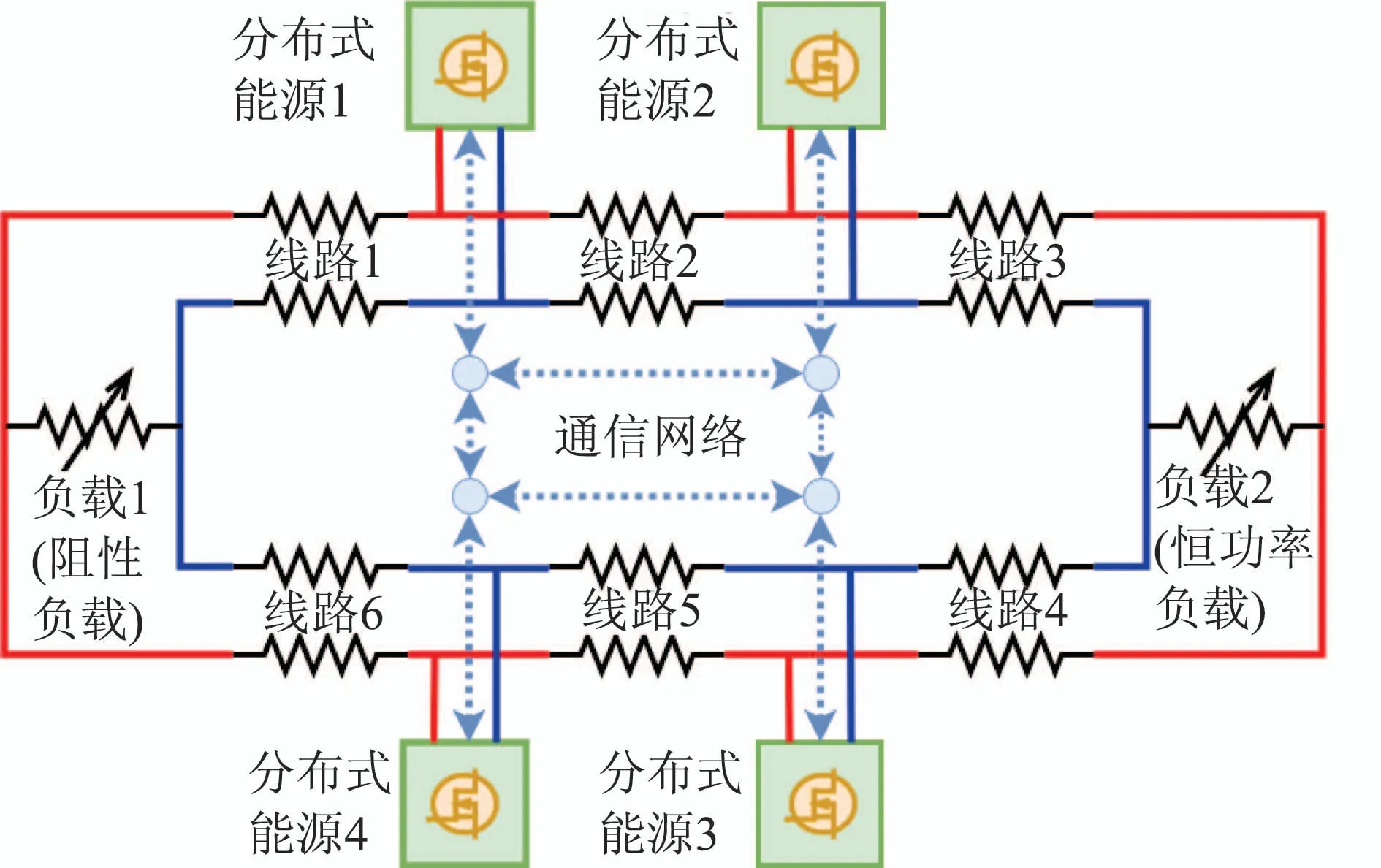
图2 环形直流微电网仿真模型Fig.2 A tested ring-bus DC microgrid

4.1 负载切换测试

在负载切换测试中,设置电流分配的比例系数为d1=d2=d3=d4=1,同时设置下垂控制系数为m1=m2=m3=m4=1.执行如下操作步骤:当t=1 s时,启用二次控制器控制器(16);当t=4 s时,将负载1从50 Ω切换到100 Ω;当t=7 s 时,将负载1从100 Ω切回至50 Ω.在仿真中选取α1=5,α2=20,经计算满足矩阵Γ特征根皆为正的条件.

仿真结果如图3–5所示.图3展示了观测器状态的演化曲线,可发现在启用二次控制器后观测状态能够实现收敛,并在负载切换后仍就逐步恢复到100 V.图4展示了4个转换器输出电流的演化曲线.开始时仅采用下垂控制,观测到输出电流之间存在稳态误差.当启用二次控制器后,输出电流达到了一致,实现了均流控制目标.图5展示了4个转换器的输出电压曲线以及它们的平均值.可以观察到平均电压在启用二次控制器后收敛到100 V,实现了电压调控目标.

图3 负载切换测试中观测状态曲线Fig.3 Evolutions of estimate states in the load step test

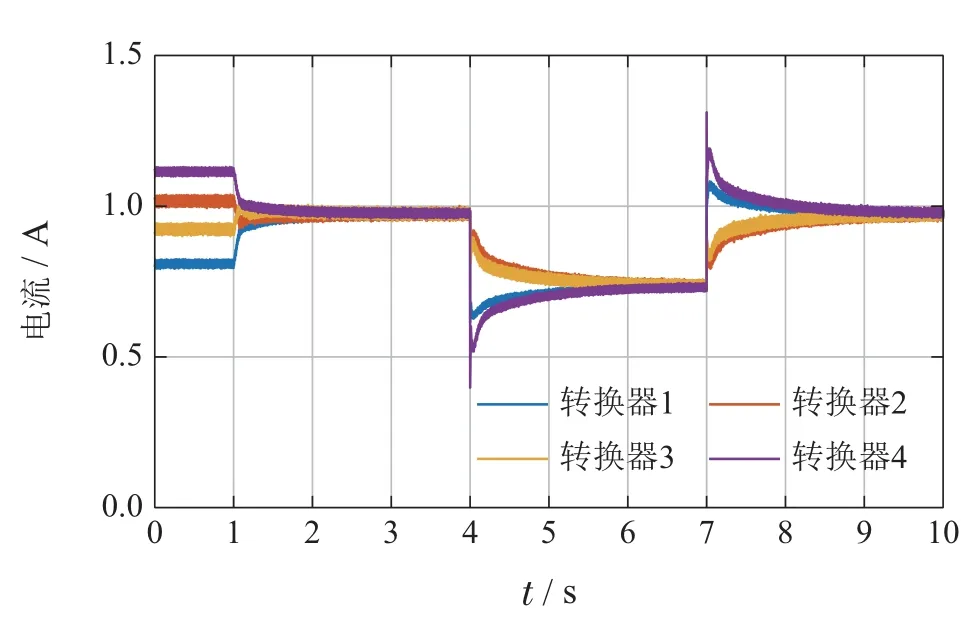
图4 负载切换测试中转换器输出电流曲线Fig.4 Evolutions of output currents in the load step test

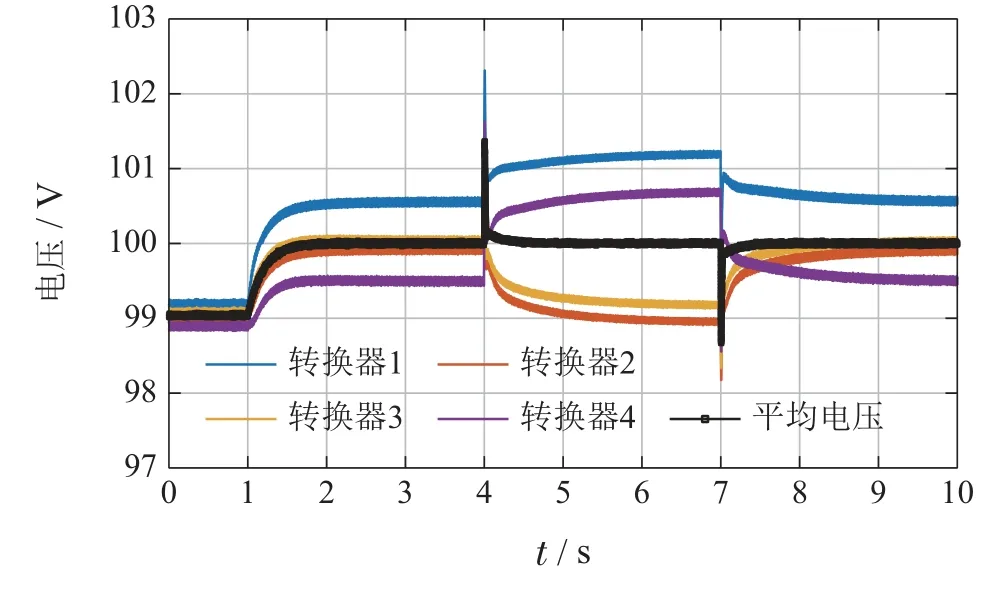
图5 负载切换测试中转换器输出电压和平均电压曲线Fig.5 Evolutions of output voltages and their average in the load step test

4.2 即插即用测试

在即插即用测试前,设置电流分配的比例系数为d1=d2=1,,同时依旧保持下垂控制系数为m1=m2=m3=m4=1.按照如下阶段执行即插即用操作,第I阶段:当t ∈[0,1)时,仅启用下垂控制;第II阶段:当t ∈[1,4)时,施加所设计的分布式二次控制器(16),其中α1=5,α2=20;第III阶段:当t ∈[4,8)时,切除第2个分布式能源;第IV阶段:当t ∈[8,12)时,将切除的第2个分布式重连.

仿真结果如图6–8所示.图6展示了观测器状态的演化曲线,图7和图8分别展示了4个转换器输出电流和输出电压的演化曲线.在第I阶段中,由于仅采用下垂控制,平均电压和电流分配皆存在稳态误差;在第II阶段,启用二次控制器后观测到转换器的输出电流实现了2比3的比例分配,同时输出电压的平均值收敛到100 V;第III阶段和第IV阶段中,对第2个分布式能源进行插拔,可观测到电流曲线和电压曲线皆能够快速恢复到稳定,剩余分布式能源节点也能够稳定到新的平衡点.当第2个分布式能源再接入到环网时,电流分配和电压调控都恢复到原先第II阶段的状态.

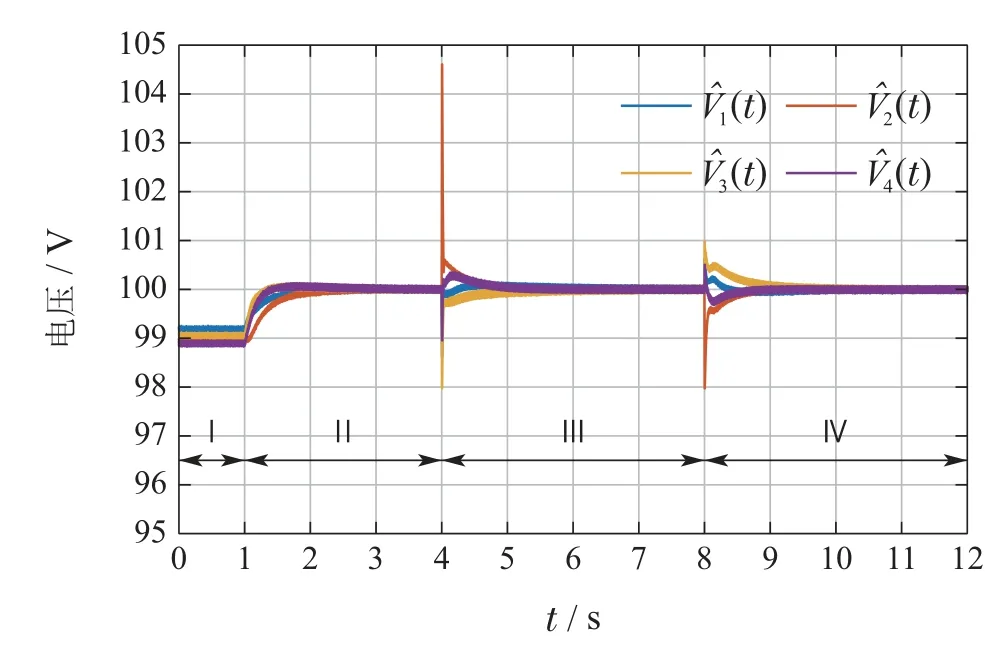
图6 即插即用测试中观测状态曲线Fig.6 Evolutions of estimate states in the plug-and-play test

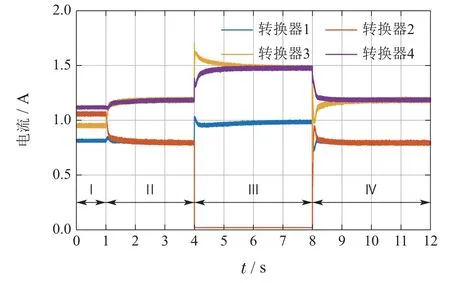
图7 即插即用测试中转换器输出电流曲线Fig.7 Evolutions of output currents in the plug-andplay test

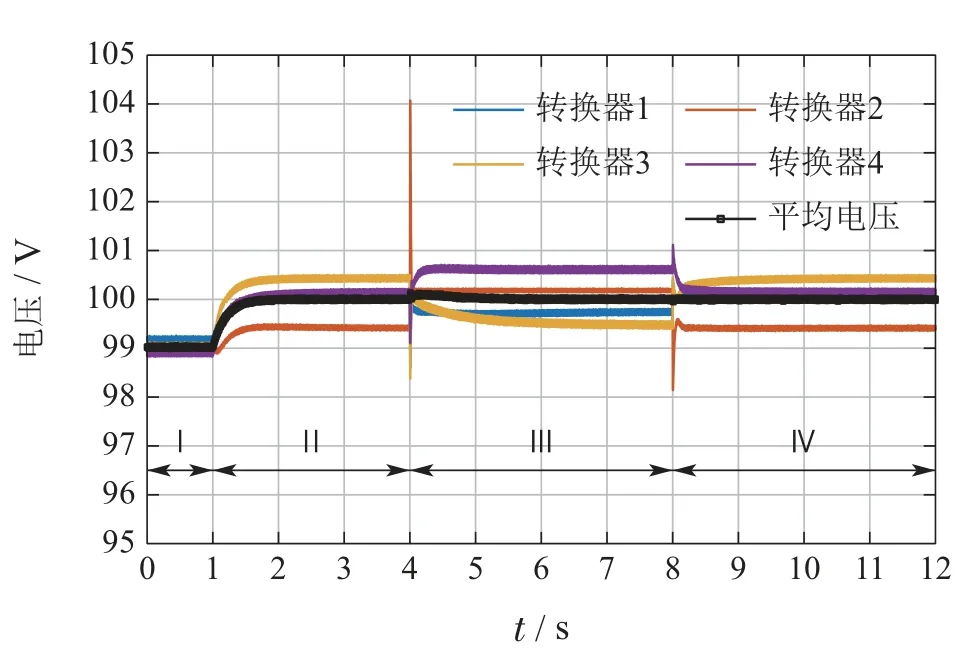
图8 即插即用测试中转换器输出电压和平均电压曲线Fig.8 Evolutions of output voltages and their average in the plug-and-play test

4.3 并网运行测试

环形直流微电网与主网的连接点在负载2处.直流系统通过一个双向交错式转换器(bidirectional interleaved converter,BIC)与主网连接.由于环网中的分布式能源的转换器已工作在电压模式下,足以维持环网的电压控制.在测试中本文对BIC采用电流环PI控制,并设置相应的电流参考值作为BIC电流环的参考输入.在仿真中,设置电流分配的比例系数为d1=d2,同时依旧采用相同的下垂控制系数m1=m2=m3=m4=1.按照下述步骤进行操作,首先设置.第I阶段:当t ∈[0,1)时,仅启用下垂控制;第II阶段:当t ∈[1,4)时,施加二次控制器(16),并设置α1=5,α2=20;第III阶段:当t∈[4,8)时,设置BIC的参考电流为;第IV阶段:当t ∈[8,12)时,设置BIC的参考电流为

仿真结果如图9–11所示.图9展示了观测器状态的演化曲线,图10和图11分别展示了4个转换器输出电流和输出电压的演化曲线.在第I阶段和第II阶段中,启用二次控制器后不仅观测器能够实现收敛,转换器的输出电流也实现了2比3的分配比例,同时输出电压的平均值收敛到100 V.在第III阶段和第IV阶段中,修改BIC电流环参考工作点,可观测到电流曲线和电压曲线皆能够恢复到稳定,并达到新的平衡点.当主网输送的功率大于环网的负载功率时,剩余功率会通过4个分布式能源按照比例消纳,此时输出电流为负.

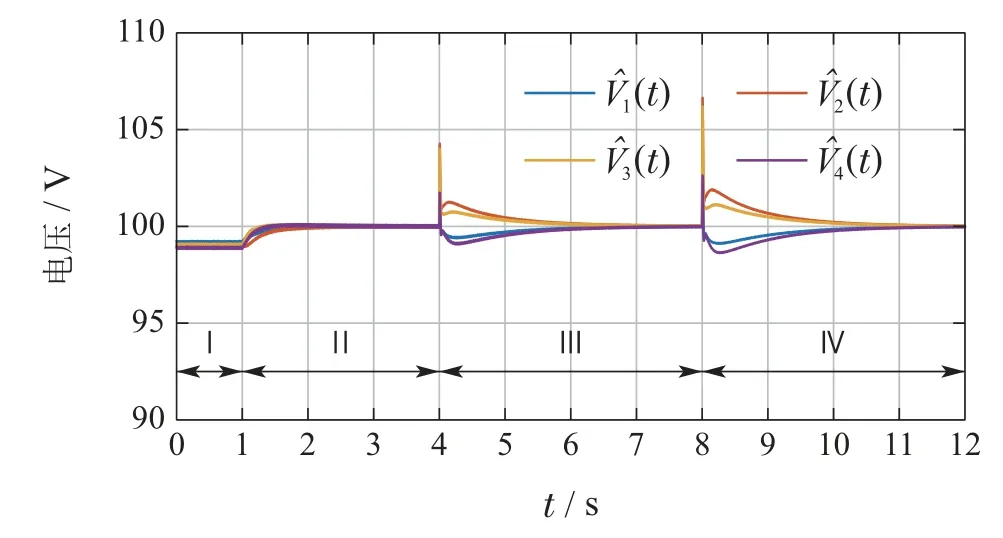
图9 并网运行测试中观测状态曲线Fig.9 Evolutions of estimate states in the grid-connected mode test

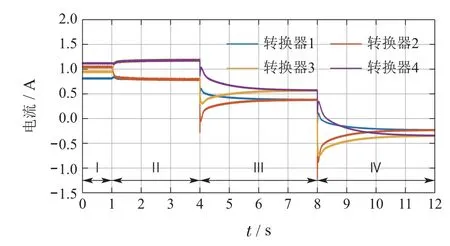
图10 并网运行测试中转换器输出电流曲线Fig.10 Evolutions of output currents in the grid-connected mode test

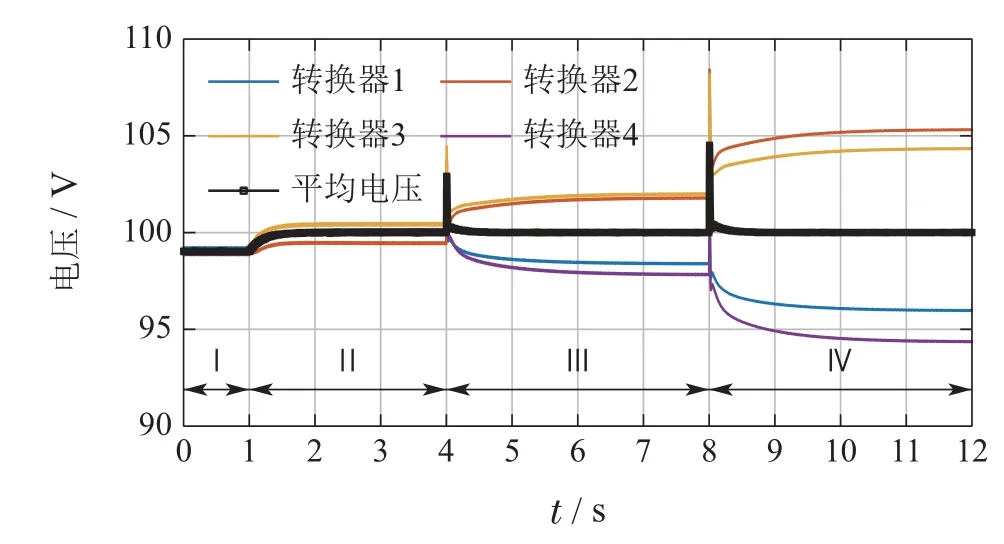
图11 并网运行测试中转换器输出电压和平均电压曲线Fig.11 Evolutions of output voltages and their average in the grid-connected mode test

5 总结

本文解决了环形直流微电网二次控制的稳定性分析问题.首先基于微电网的控制目标设计了3种误差状态,并设计了局部观测器估计微电网中所有分布式能源节点的平均电压.然后基于观测器状态和电流误差设计了动态反馈控制器,并通过解耦环形直流微电网的潮流代数方程,得到误差状态的闭环系统.基于线性系统理论和矩阵特征根扰动的分析方法,给出了闭环系统的稳定性条件,并进一步阐释误差系统的平衡点与控制目标间的等价关系.最后通过仿真验证了所设计的控制器在即插即用性和并网运行时的有效性.未来研究工作将考虑网络安全因素下的直流微电网系统的控制器设计与稳定性分析问题.