Electronic structures of vacancies in Co3Sn2S2*

Yuxiang Gao(高于翔) Xin Jin(金鑫) Yixuan Gao(高艺璇)Yu-Yang Zhang(张余洋) and Shixuan Du(杜世萱)

1Institute of Physics and University of Chinese Academy of Sciences,Chinese Academy of Sciences,Beijing 100190,China

2CAS Center for Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100190,China

3Beijing National Center for Condensed Matter Physics,Beijing 100190,China

4Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords: first-principle calculations,vacancies,localized bound states,orbital hybridization

1. Introduction

Co3Sn2S2,a newly discovered Weyl semimetal, has received much attention in recent years.[1-7]Different from other Weyl semimetals such as TaAs, TaP, NbAs, and NbP reported earlier,[8-10]Co3Sn2S2has intrinsic magnetism and thus breaks time-reversal symmetry.[11-14]Fermi arcs and Weyl nodes in this material have been observed under an external magnetic field and finely tuned through the control of magnetization.[1,15-19]Moreover, because the Weyl nodes in Co3Sn2S2are close to the Fermi level, a large intrinsic anomalous Hall effect was predicted and experimentally observed.[20-25]Besides, multiple novel physical properties were also observed, including anomalous Nernst effect[26-28]and anisotropic negative magnetoresistance.[25]

Defects play key roles in a wide range of materials because they are inevitable in real materials and notably influence the physical properties of the hosts.[29-35]The defects in GaN significantly affect its electrical and optical properties, seriously degrading the performance and reliability of devices.[32,33]While several types of defects were found to increase the catalytic performance for the hydrogen evolution reaction,[34,35]carbon dioxide reduction reaction,[36]and photocatalytic reaction.[37]Very recently,it is found that a substituted indium impurity in Co3Sn2S2introduces a striking localized bound state.[38]Besides, single S vacancies in a Sterminated surface introduce spin-orbit polaron.[39]Thus, a theoretical study of the electronic structures of various defects in Co3Sn2S2is necessary for future experimental investigations.

In this paper, using quantum mechanical calculations based on density functional theory (DFT), we calculate the band structures and magnetic properties of bulk Co3Sn2S2with several functionals at different levels. It is found that the positions of Weyl nodes and the magnetic moments given by generalized gradient approximation (GGA) implemented by Perdew-Burke-Ernzerhof (PBE) are consistent with the reported experimental results. While the Heyd-Scuseria-Ernzerhof screened hybrid functional (HSE06) highly overestimates the magnetic moments and a gap is found near the Fermi level, which is different from the semimetal nature of Co3Sn2S2. We then exploit PBE functional to further investigate the electronic structures and formation energies of defects on S-terminated and Sn-terminated surfaces. We find that vacancies in the S-terminated surface have a significant influence on its band topology. A single sulfur vacancy (VS) induces spin-polarized localized bond states in the gap near the Fermi level. When two or three S vacancies approach, they interact with each other.The localized states hybridize and form bonding states as well as anti-bonding states. For the Sn vacancy on the Sn-terminated surface,the defect levels are not found in the gap near the Fermi level but are merged with the valence bands. These results may help to understand this compound more comprehensively and would be beneficial for further investigations.

2. Methods

First-principle calculations based on density functional theory (DFT) were performed by using the Viennaab initiosimulation package (VASP).[40,41]The projector augmented wave (PAW)[42]method was applied. Exchange-correlation functionals at different levels were used, including local density approximation (LDA), Perdew-Burke-Ernzerhof(PBE),[43]modified Becke-Johnson (mBJ),[44,45]and Heyd-Scuseria-Ernzerhof screened hybrid functional (HSE06).[46]A kinetic energy cutoff of 400 eV was used for bulk and pristine surfaces calculations. A kinetic energy cutoff of 270 eV was used for surfaces with defects.

A primitive cell of bulk Co3Sn2S2contains 3 Co atoms,2 Sn atoms, and 2 S atoms in a rhombohedral crystal structure (R-3m). The slab models containing six Co-Sn layers and extra S,Sn, and Co3-Sn layers were used to simulate the S-terminated, Sn-terminated, and Co-terminated surfaces, respectively. Single vacancies were simulated in 4×4 supercells, while two or three vacancies were simulated in 5×5 supercells. For structural relaxations, the atoms between the middle two Co3-Sn layers were constrained and other atoms were fully relaxed.The vacuum layers of the slab models were larger than 15 ˚A.

For bulk Co3Sn2S2,thek-points sampling was 8×8×8,generated by Monkhorst-Pack grids with the origin at theΓpoint.[47]For pristine S-terminated, Sn-terminated, and Coterminated surfaces of Co3Sn2S2, thek-points sampling was 8×8×1. For surfaces with vacancies, thek-points sampling was only theΓ-point. The structures were relaxed until the residual force on each atom was smaller than 0.01 eV/˚A.The convergence criterion of electronic relaxation was 10-6eV for the bulk and pristine surface calculation and 10-4eV for the vacancies calculations. The Gaussian smearing method was used for density of states calculations with a smearing width of 0.02 eV.Thek-mesh for the DOS calculation was 7×7×1.

3. Results and discussion

Firstly, we calculated the electronic structures of bulk Co3Sn2S2. This compound possesses a quasi-twodimensional structure with the Co3-Sn layer sandwiched by Sn and S layers,as shown in Fig.1(a). The lattice parameters calculated with various functionals are summarized and compared with previous works in supporting material Table S1.We calculated the band structures and magnetic moments in a primitive cell with different functionals. The magnetic moments calculated with LDA, PBE, meta-GGA, and hybrid functionals applied are summarized in supporting material Table S2. The band structures were calculated along high symmetry paths in the first Brillouin zone,as shown in Fig.1(e).

The spin-polarized band structures in a Co3Sn2S2primitive cell with PBE functional is shown in Fig.1(b). The separation of spin-up and spin-down channels indicates a ferromagnetic order and the magnetic moment is 0.35μBon each Co atom, which is consistent with previous experiments.[24]The valence and conductance bands inverse and form a nodalring, which is shown as a pair of crossing points close to the Fermi level in the spin-down channel near theLpoint. Then the nodal-ring decays into a pair of Weyl points when spinorbital coupling(SOC)is considered,as shown in Fig.1(f). A small gap is opened near theLpoint because the Weyl points are very close to the high symmetry line but not in it. The positions of the nodal-ring and Weyl points are highly consistent with previous works.[16]

We also calculated the electronic structures of bulk Co3Sn2S2with functionals at higher levels of the Jacob ladder, which most of time generates better electronic structures near the Fermi level. The band structures calculated with the mBJ functional are shown in Figs.1(c)and 1(g). It is clearly shown that only one crossing point near theUpoint remains and the other one is missing. For the HSE06 functional,a gap appears near the Fermi level in the spin-polarized band structure,as shown in Fig.1(d),which is different from the experimental observation. Moreover, the HSE06 functional highly overestimates the magnetism of Co3Sn2S2. The magnetic moment calculated with HSE06 functional is 0.48μBon each Co atom, which is nearly 50% larger than the experimental reported value. Considering the fact that Co3Sn2S2possesses a moderate electronic correlation,[19]this significant deviation may contribute to the overestimation of the electronic correlation strength by these functionals. Thus,considering the position of Weyl points and the calculated magnetic moments,we found that the semi-empirical PBE functional captures both features among all the functionals, so it is exploited for later investigations.

We then calculated the surface energies of surfaces with different terminations, which determines whether a surface is easy to cleave. The surface energies are calculated using the following formula:

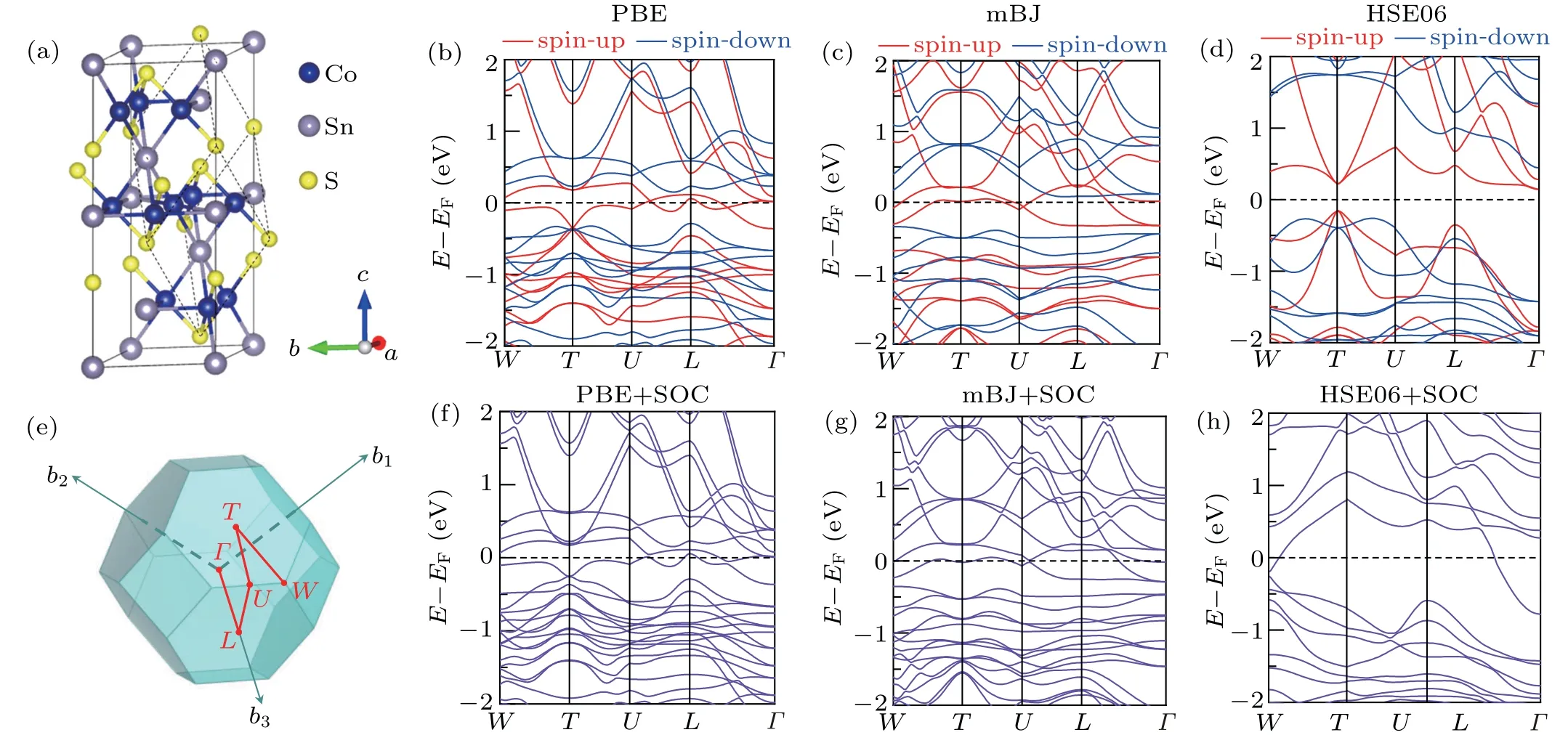
Fig.1. The atomic structure and electronic structures of bulk Co3Sn2S2. (a)The atomic structure of Co3Sn2S2 in a conventional cell containing three formulas.The dashed line indicates the primitive cell of Co3Sn2S2. The blue,grey,and yellow balls represent Co,Sn,and S atoms,respectively. (b)-(d)Spin-polarized band structures of Co3Sn2S2 in primitive cell with PBE,mBJ,and HSE06 functionals,respectively. (e)The first Brillouin zone showing high symmetry paths.(f)-(h)Band structures of Co3Sn2S2 considering spin-orbital coupling with PBE,mBJ,and HSE06 functionals,respectively.

The surface energies of S-terminated,Sn-terminated,and Co-terminated surfaces are summarized in supporting material Table S3. It is found that Co-terminated surfaces possess the highest surface energy of 0.080 eV/˚A2among the three surfaces,which is close to the value of Si(111)surface.[49]It indicates that Co-terminated surfaces are hard to cleave,which explains the fact that the Co-terminate surface is hard to find experimentally. While for Sn-terminated and S-terminated surfaces,the surface energies are 0.034 eV/˚A2and 0.032 eV/˚A2,respectively,which are larger than that of graphite,[50]but are close to that of the YBa2Cu3O7(001) surface.[51]The surface energies of S-terminated and Sn-terminated surfaces are half the value of Co-terminated surface. The reason is that to form S-terminated and Sn-terminated surfaces, only three Co-Sn bonds need to be broken. While for a Co-terminated surface, besides three Co-Sn bonds, extra three Co-S bonds are also need to be broken. And the Co-S bond is stronger than the Co-Sn bond, which can be estimated by its smaller bond length.

Then we investigate the formation energies of S vacancies that appear in the S-terminated surface. According to the surface energy calculations,S-terminated surfaces are easy to cleave. Indeed, these surfaces are frequently observed in experiments[15,17,39,52]with randomly distributed S vacancies,including mono-sulfur vacancy(VS),di-sulfur vacancy(VS2),and tri-sulfur vacancy (VS3). The formation energies of different types of S vacancies are summarized in Table 1. The formation energies of different defects were calculated using the following formula:

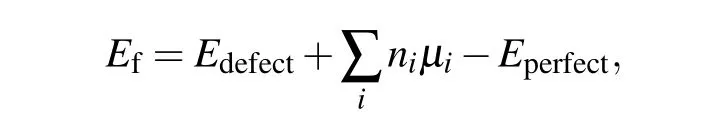
whereEdefect(Eperfect) is the total energy of the system with(without) defects.niis the number of atoms being removed from the host. Andμiis the chemical potential of the removed atom. The chemical potentials are in the ranges of

whereES,ESn,andECoare the energy per atom of S,Sn,and Co in pure bulk form,andECo3Sn2S2is the total energy of the bulk Co3Sn2S2unit cell.

After losing a S atom on a S-terminated surface, three Co atoms underneath the vacancy site are exposed, as shown in Fig. 2(a). A kinetic energy cutoff of 270 eV was used for defective surface calculations. The three Co atoms are displaced slightly inward. The distance between the neighboring Co atoms changes from 2.58 ˚A in a pristine S-terminated surfaces to 2.51 ˚A after the formation of a VS. The formation energy of VSon the S-terminated surface is 2.36 eV at the Srich limit and 1.14 eV at the S-poor limit, which is smaller than that of VSin monolayer MoS2and WS2,[53,54]leading to a larger chance to form VSon S-terminated surfaces.

The electronic structures of VSwere calculated, which are shown in Fig.2(b). Two bands appear inside the gap near the Fermi level at the spin-down channel,which are degenerate at theΓpoint and almost degenerate with only 1-2 meV energy difference atMandKpoints. The localized density of states(LDOS)at the vacancy site,which is shown in Fig.2(c),clearly shows a peak at the spin-down channel with the energy of 0.05 eV above the Fermi level. These results indicate that VSon the S-terminated surface induces a magnetic localized bound state inside the gap of the spin-down channel near the Fermi level.

The interactions of VSwere then investigated. The formation energies of a di-sulfur-vacancy (VS2) and a tri-sulfurvacancy(VS3)in different configurations are shown in Table 1.It is found that the formation energies of VS2and VS3are almost twice and three times that of VS,respectively,suggesting that the interactions between S vacancies are not strong. This small energy difference among VS,VS2,and VS3may explain the random distribution of sulfur vacancies in STM images of the S-terminated surface.[15,20]

Table 1. Formation energies of vacancies on Co3Sn2S2 surfaces with different terminations.

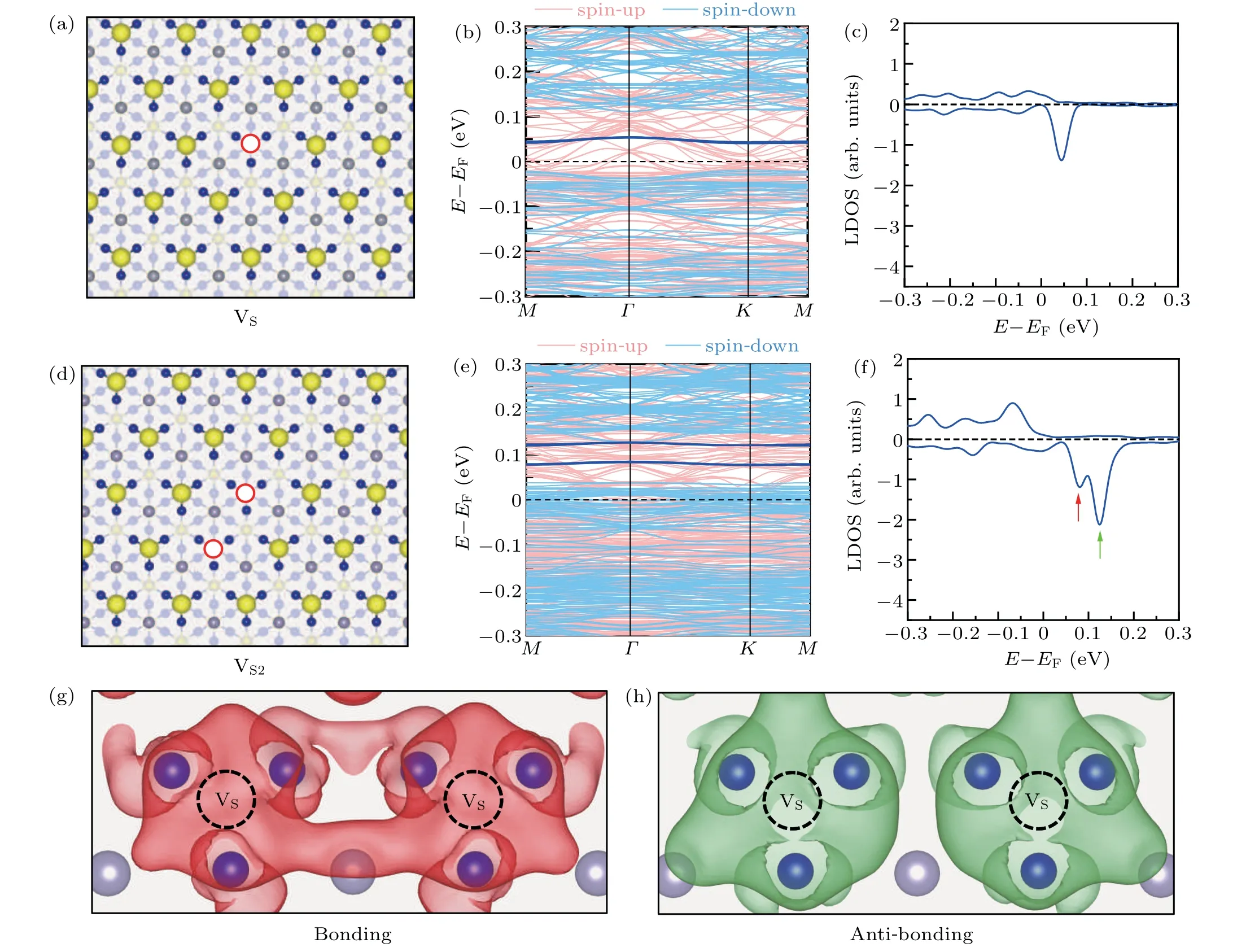
Fig.2. Localized bond states induced by VS and VS2 on a S-terminated surface of Co3Sn2S2. (a)The atomic configuration of a S-terminated surface containing a VS. The red hollow circle represents the S vacancy. (b)The band structure of the S-terminated surface with a VS. The dark blue lines are the localized bound states. (c)Spin-polarized localized density of states(LDOS)projected on VS. (d)The atomic structure of a S-terminated surface with VS2. (e)The band structure of the S-terminated surface with VS2. (f)Spin-polarized LDOS projected on VS2.The two defect states are labeled by red and green arrows. (g)and(h)The charge distributions of the two defect states marked by the red and green arrows in(f),respectively. An isosurface of 8.0×10-5 e/Bohr3 is used.

Though the interaction between neighboring S vacancies does not significantly lower the formation energy, it strongly affects the localized bound states inside the energy gap. The atomic structure of VS2is shown in Fig.2(d). The electronic structures of the S-terminated surface with di-vacancies are shown in Figs.2(e)and 2(f).The band structure and the LDOS indicate that two defect states appear inside the gap near the Fermi level. Each defect state contains two almost degenerate bands. The energies of these two localized bond states are 0.04 eV and 0.08 eV higher than the gap edge,pointed out by the red and green arrows in Fig.2(f). Interestingly,the localized bond state of VSis 0.06 eV higher than the gap edge, in the middle of the two localized bond states of VS2. So these two defect states in VS2are more likely to be the consequence of the orbital hybridizations of the defect state of VS.

The spatial distributions of the two localized states induced by the sulfur vacancies are plotted in Figs. 2(g) and 2(h). As shown in Fig. 2(g), there is a significant electron accumulation between the two sulfur vacancy sites,indicating that the defect state sitting at 0.04 eV above the gap edge(red arrow in Fig. 2(f)) presents a bonding orbital feature. While,as shown in Fig.2(f),the charge distribution of the defect state sitting at 0.08 eV above the gap edge(green arrow in Fig.2(f))reflects an anti-bonding orbital feature. Thus, we conclude that when two VSin VS2interact with each other, the localized bond states hybridize and form a bonding state as well as an anti-bonding state. It should be mentioned that,because the isolated defect level is unoccupied,although the energy is lowered by the hybridization,the bounding state is still above the Fermi level.

Then we considered three sulfur vacancies cases. The three sulfur vacancies are built in two ways, triangular shape and linear shape. The triangle VS3contains three S vacancies combined in an equilateral triangle,as shown in Fig.3(a).The band structure of triangle VS3,as shown in Fig.3(b),also shows two group defect states inside the gap near the Fermi level. Different from the feature in the VS2case, the defect state near the band edge shows a significant broadened bandwidth. The LDOS project on the vacancy site,which is shown in Fig. 3(c), shows two peaks at the energies of 0.04 eV and 0.13 eV above the Fermi level, respectively. Obviously, the peak marked by the red arrow is much broader.

Fig.3. Localized defect states induced by three sulfur vacancies on the S-terminated surface of Co3Sn2S2. (a)-(c)The atomic configuration,band structure,and LDOS of a S-terminated surface with three sulfur vacancies in a triangular shape. (d)-(f) The atomic configuration, band structure, and LDOS of a S-terminated surface with three sulfur vacancies in a linear shape. The two groups of defect states are labeled by red and green arrows in(c)and(f).

The line VS3contains three S vacancies in a row,as shown in Fig.3(d). The band structure of line VS3(Fig.3(e))shows that the defect states are further broadened and split. The LDOS projected on the vacancy site is shown in Fig.3(f). Besides the two peaks with the energies of 0.05 eV and 0.14 eV above the Fermi level(red and green arrows in Fig.3(f)),there is a small bump in between, representing the splitting of the defect states.The electronic structure of line VS3is more complicated than that of triangle VS3and that may account for the lower symmetric configuration of line VS3. It is also noting that the energy differences between the two peaks in LDOS of the triangle and line VS3are both 0.09 eV, larger than that in the VS2case(0.04 eV).The increasing energy splitting of the bonding states and the anti-bonding states indicates that the interaction between the VSin VS3is larger than that in VS2.

The charge density distributions of the defect states in VS3were then calculated. The charge density distribution of the lower defect states (marked by the red arrows in Figs. 3(c)and 3(f)) shows a bonding orbital feature (supporting material Figs. S1(a) and S1(c)). The higher energy defect states(marked by the green arrows in Figs. 3(c) and 3(f)) show an anti-bonding orbital feature (supporting material Figs. S1(b)and S1(d)). Thus, we conclude that the orbital hybridization and the formation of the bonding/anti-bonding states are universal features when sulfur vacancies are closed to each other.

We then considered the single Sn vacancy on a Snterminated surface. The atomic structure is shown in Fig.4(a).The formation energy is 0.41 eV at the Sn-rich limit and-0.81 eV at the Sn-poor limit. The band structure of a Snterminated surface with a Sn vacancy is shown in Fig. 4(b).From the band structure calculations, it is found that the Snterminated surface with a VSnis a semimetal with a 0.4 eV bandgap in the spin-down channel.It is also found that there is no defect state in the gap of the spin-down channel. By checking the LDOS plot projected on the vacancy site(as shown in Fig.4(c)),we found a peak at the energy of-0.35 eV,indicating that the defect level is merged with the valence band of the surface.

The charge density distributions decomposed to different energies were analyzed to identify the defect states. As shown in Fig. 4(d), the spatial distribution of the peak at-0.35 eV(marked by the blue arrow in Fig. 4(c)) reveals a three-fold feature around the Sn vacancy. This indicates that the defect states induced by a single Sn vacancy are also localized bond states. The side view of the spatial charge density distribution around the peak of the defect states, which is shown in Fig. 4(e), indicates that the charge distributes on the top two layers. The spin-polarized projected density of states(PDOS)on surface atoms,as shown in Fig.4(f),also shows a peak with the energy of-0.35 eV,corresponding to the energy of the defect states. So, the localized bound states induced by the Sn vacancy are merged with the trivial valence band.

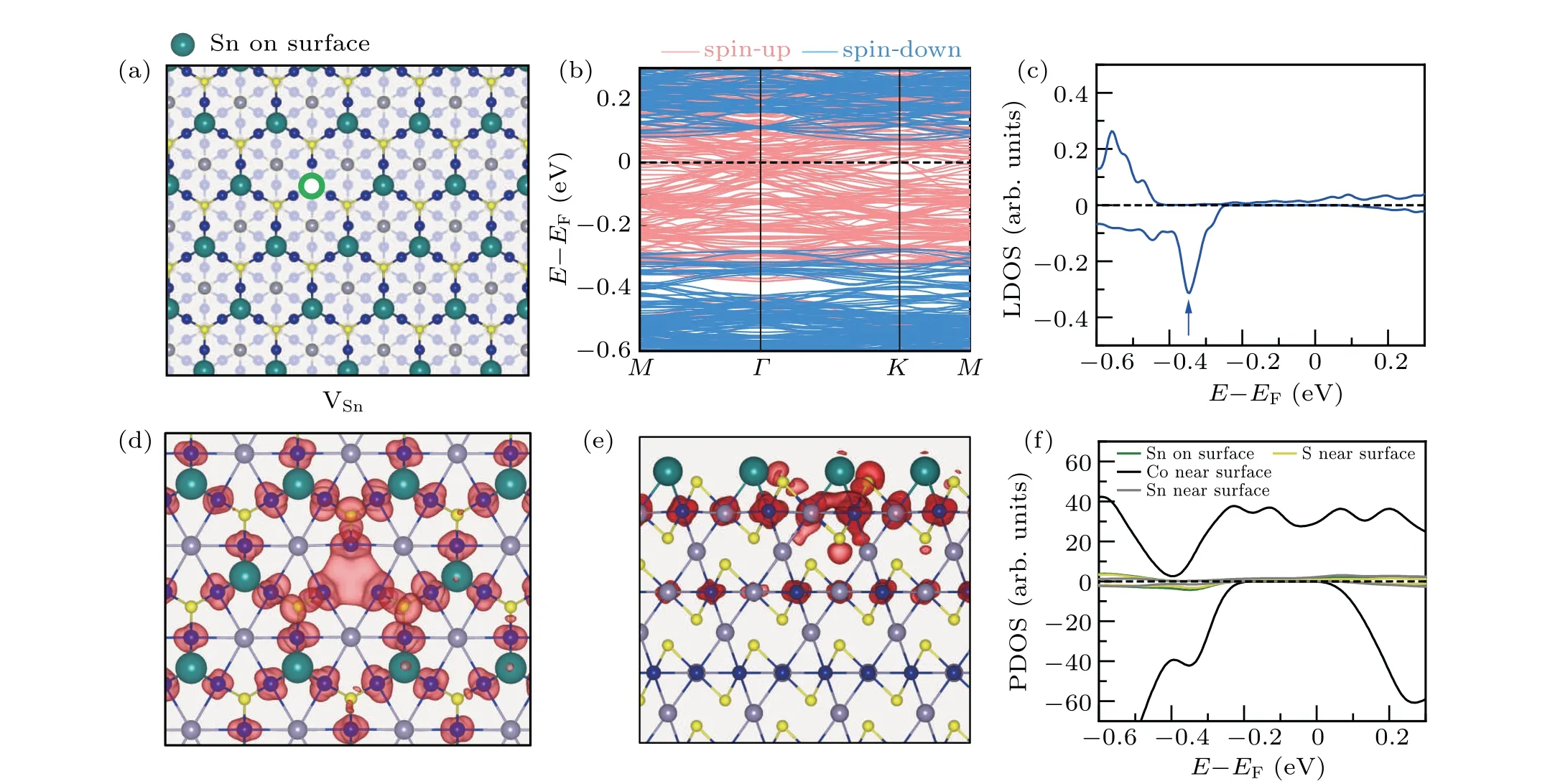
Fig.4. Electronic structure of the Sn-terminated surface with a single Sn vacancy. (a)The atomic structure of a Sn-terminated surface with a VSn. Big green balls represent the top-layer Sn atoms and the green hollow circle represents the single Sn vacancy. (b)The band structure of the Sn-terminated surface with VSn. (c)Spin-polarized LDOS projected on the Sn vacancy site. (d)and(e)Top and side views of the charge distribution of the defect state marked by the blue arrow in(c),respectively. An isosurface of 8.0×10-5 e/Bohr3 is used. (f)Spin-polarized projected density of states(PDOS)of Sn atoms on the surface as well as Co,Sn,and S atoms near surface.

4. Conclusion and perspectives

We calculated band structures and magnetic moments of bulk Co3Sn2S2with functionals at different levels. It is found that GGA functional in the PBE form reproduces the positions of Weyl points observed in previous experiments. We then investigated the influence of vacancies on the electronic structure of S-terminated and Sn-terminated surfaces. For Sterminated surfaces, a localized bond state induced by VSis found inside the gap.When VScombine and interact with each other, the localized bond states hybridize and generate bonding states as well as anti-bonding states. For Sn-terminated,localized states are merged inside the valence band, thus not observed near the Fermi level.