Phase-and spin-dependent manipulation of leakage of Majorana mode into double quantum dot*

Fu-Bin Yang(羊富彬), Gan Ren(任淦), and Lin-Guo Xie(谢林果)

Department of Physics and Key Laboratory of Photonic and Optical Detection in Civil Aviation,Civil Aviation Flight University of China,Guanghan 618307,China

Keywords: spin-dependent coupling,Majorana bound states,double quantum dots

1. Introduction

Majorana bound states[1-5]are at the forefront of condensed matter physics in the topological quantum computation. In fact, Majorana bound state can be realized by detecting the hybrid Majorana quantum dot (QD) system,[6,7]which is used as a spectrometer of Majorana by performing the bias-dependent spectroscopy.[8]Specifically,Majorana bound states can be realized at the ends of a one-dimensional semiconducting wire with spin-orbit coupling.[9]The recent focus on the Majorana bound states is the perspective of interferometer characteristics in Majorana quasiparticles.[10-15]An Aharonov-Bohm interferometer has been studied through controlling the phase factor to achieve the perspective of single source excitation.[15,16]The interference effects were studied[17,18]in the hybrid Majorana QD system through Green’s function method. These results undoubtedly give a method to elaborate experimental realizations in the hybrid Majorana QD system. Also, recent literature gives the spindependent effect of such an interferometer to verify the correlation between the Kondo-Coulomb repulsion and Majorana bound states.[19-21]The QD-coupled Majorana wire was used to detect the Majorana bound states under the spin-polarized condition.[22-26]They explored the spin properties inside the Majorana by constructing the coupling between the electrode and the Majorana QD system.[27-29]

Studying the spin-dependent properties plays an important role in the hybrid Majorana QD system. However, the research is still insufficient in explaining the spin properties of such hybrid Majorana QD system. The Majorana zero mode can be detected in recent setup through the QD density of states (DOS). Here, we show that the multi-QD system can also be used to manipulate the Majorana zero mode.

2. Model and theory

As shown in Fig.1,we consider an interferometer which consists of double quantum dots coupled to a Majorana topological superconducting wire and a metallic (or a ferromagnetic)lead. When the tunnel couplings between the Majorana bound states and the QDs are fixed to a specific phase, the DOS becomes unchangeable irrespective to the coupling between the Majorana and the double quantum dots. The detection of Majorana mode in Majorana wire without electrode coupling has been discussed.[9,15]In the ring structure, it allows us to analytically explore the effect of phase change factor on the Majorana leakage into(out)of the double quantum dots. Also, we incorporate the situation of spin dependence into the lead,which is sensitive to the unique interaction of the double quantum dots. We consider the noninteracting regimes of the double quantum dots. We provide an exact retarded Green’s function to calculate the DOS of the two dots by using the equation of motion (EOM) method.[30,31]While the noninteracting quantum dot is enough for obtaining the exact expression for the Green’s function,it can also show the information about the Majorana signature co-existing together with some related phenomena.[32,33]Hence,the Hamiltonian can be expressed as

We describe the DOS in order to describe the phasedependent characteristics of the system. We focus on these quantities to explore the coexistence and interplay of phase and spin couplings of the system. We use the EOM procedure to obtain the full retarded Green’s function,which can be written as the following form:

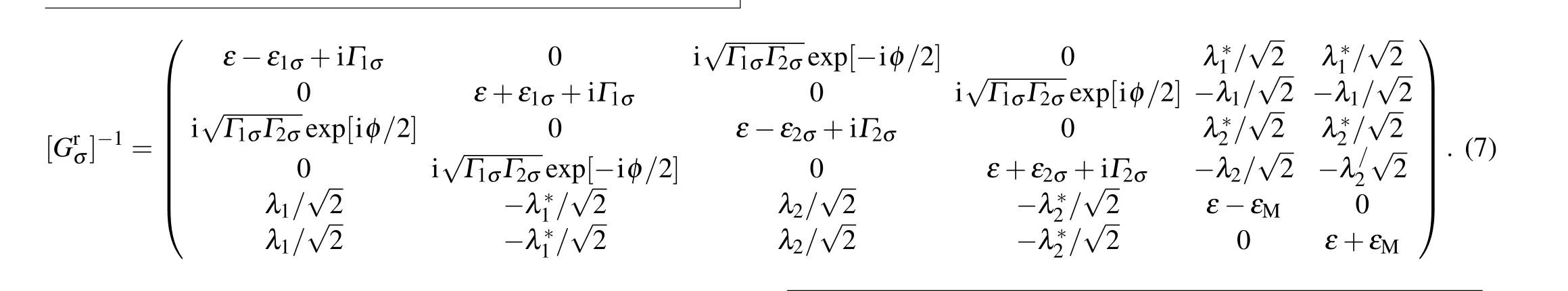
Fig. 1. Schematic diagram of Majorana-double quantum dots system in which single Majorana mode γ1 is located at the edge of a one-dimensional Majorana topological superconducting wire which is coupled to double quantum dots attached to a single metallic lead, λ1(2) is the effective coupling strength between Majorana bound states and the quantum dot1(2), V1σ(2σ)represents the coupling strength between quantum dot1(2) with metallic lead,and Φ is the magnetic flux threading through the ring of the system.

3. Results and discussion

In this section,we give the numerical results under different coupling effects on the phase. We first study the properties of DOS under different values of phaseφin Fig. 2.We choose the same coupling strength asΓ1σ=Γ2σ=Γand|λ1| =|λ2| =λfor the same DOS of the two QDs. The DOS exhibits a relatively flat region atε= 0 and a resonance aroundε=±1.0 in Fig. 2(a). The bimodal structure gradually gathers towardsε=0 and a more pronounced resonance peak structure appears in Fig.2(b). The bimodal structure disappears instead of a single resonance peak structure in Fig. 2(c). The characteristics of phase dependence can be explained by the diagonalization of the central Majorana QD Hamiltonian. The resonance of DOS is found to be related to the matrix of the retarded Green’s function. Namely, the position of resonance is determined by the zero point of the

Fig. 2. Densities of states under different values of phase φ threading through the ring of the system. The other parameters are chosen as follows:εM=0,ε1σ =ε2σ =0,Γ1σ =Γ2σ =0.5Γ0,λ1=λ2=0.5Γ0,where Γ0 is chosen as the unit of the energy.

It should be noted that that in addition to the values ofΓandφ, the formant of DOS is also related to the increase of the coupling constant. This coupling effect leads to an asymmetric structure of the energy levels. From the perspective of the real and imaginary parts of the specific Green’s function of the two QDs, we will find the influence of such an asymmetric structure on Majorana bound state ifλ1/=λ2. For comparisons, we present the DOS under different values of the coupling strengthλ2in Fig. 4. The DOS shows different behaviors,based on which one can see whether there are Majorana bound states in this system. A resonance structure still exists aroundε=0 with the value ofλ2changing as shown in Fig. 4(a). Butλ2induces the Majorana modes to changeρ2σaroundε=0 and shifts toward the large energy and it finally shows a transition from antiresonance to resonance as indicated in Fig. 4(b). The presence of the Majorana modes efficiently dissolves the antiresonance point in the DOS while inducing a resonance to appear at the same energy position.Therefore, we can conclude that such a relationship is sufficient to show the importance of the coupling relationship between Majorana and QDs. We believe that this work can be helpful in the relevant experiments.

Fig.3. Specific DOSs varying with φ for the cases of[(a),(b)]the same coupling strength: Γ1σ =Γ2σ =Γ,λ1=λ2=λ;[(c),(d)]different values of coupling λ2. The other parameters are εM=0.0,ε1σ =ε2σ =0,λ1=0.1,Γ0,Γ1σ =Γ2σ =0.1Γ0.

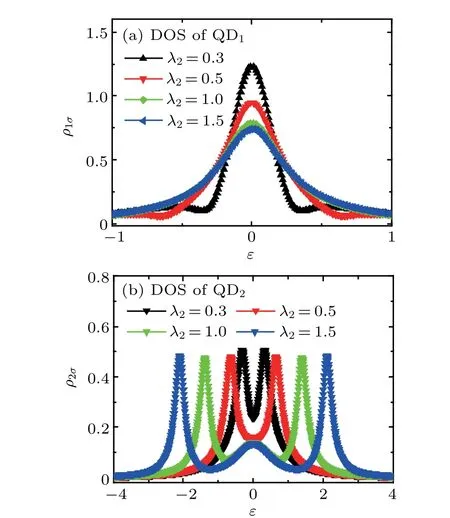
Fig. 4. DOSs under different coupling strengths, with parameters being Γ1=Γ2=0.5,λ1=0.5,and φ =0.

Finally,we consider the spin-dependent lead by introducing a definition of spin polarization strengthpof the lead-dot coupling(p=(Γ-nσΓn¯σ)/(Γ+nσΓn¯σ)). We then define the parallel case in Figs.5(a)and 5(b). Namely,Γ1↑↓=Γ2↑↓=1±pis the spin-up and spin-down coefficients of the lead. Eachρ1(2)↑atε= 0 decreases to a minimum value and the resonance is weakened as the value ofpincreases (Fig. 5(a)). However,each increases with the value ofpincreasing(Fig.5(b)).The DOS atε=0 shows anti-resonance(resonance)structure at small (large)p. The anti-resonance varies with resonance transformation aroundε=0 whenpincreases fromp=0.6 top=0.9. The value for the spin-down DOS is larger than that for the spin-up DOS as indicated in Figs. 5(a) and 5(b).Namely, the spin-down mainly contributes to the total DOS in the parallel configuration. Unlike the coupling between electrodes and quantum dots, the spin-down is the main spin coupling between Majorana bound states and quantum dots.The Majorana mode is assumed to be provided by a fully polarized spin-down.[24]When we consider the spin-dependent coupling, the quantum dot will be changed by the spin coupling in the electrode. Whenpincreases, the corresponding spin-down coupling is strengthened.The spin-down characteristics are significantly affected,which is beneficial to the system to measure the spin properties of the Majorana hybridized quantum dot system.

We further explore the DOS in the antiparallel couple case (Γ1↑↓=1±p,Γ2↑↓=1∓p), and the results are shown in Figs. 5(c) and 5(d), respectively. Unlike the parallel couple case,ρ1increases withpincreasing, the value of antiresonance decreases aroundε=0, and the peak structure at other energy levels increases. TheΓ1↑increases withpincreasing, whileΓ2↑decreases aspincreases. Meanwhile,ρ2exhibits an inversion whenpreaches a large value due to the effects of down-spin. The original resonance transforms into an anti-resonance structure, which can be used to explain the origin of the major spin-down properties.

Fig.5. DOSs with different values of spin polarization strength p,showing[(a),(b)]parallel lead alignment,and[(c),(d)]anti-parallel coupling state between lead and two QDs,with other parameters being εM=0,ε1σ =ε2σ =0,λ1=λ2=0.5Γ0,and φ =0.

4. Conclusions

In summary, we have studied the physical phasedependent properties of the double quantum dots coupled to a Majorana nanowire in a controlled parameter regime. The DOSs of the two quantum dots exhibit different resonance and anti-resonance behaviors driven by different phases and different coupling competitions. The DOS exhibits a formant whenφ=2π. But the resonance structure shields and the bimodal structure gradually gathers whenφ=0.5πand 1.5π. We also studied the DOSs of electrons under different spin polarization intensities. A characteristic of the spin-down DOS panel changes more strongly than that of the spin-up DOS. We believe that the model discussed presents a good way to effectively verify the spin-dependent mode in the hybrid Majorana QD device.